回转轴空间六方位转角误差辨识解析与补偿实验分析＊

张 颖 于 博 胡 月

（①长春光华学院机械工程学院，吉林 长春 130012；②长春工程学院机电工程学院，吉林 长春 130012；③河北民族师范学院物理与电子工程学院，河北 承德 067000）

被誉为“工业母机”的数控机床在机械制造行业有着无比重要的地位，在国务院发布的《国家中长期科学和技术发展规划纲要》中，已经将“高档数控机床与基础制造技术”列为国家科技重大专项[1-3]，由此可见，国内对高性能制造装备的需求正在稳步提升。五轴数控机床是复杂零部件加工的重要手段[4-6]，机床精度直接影响和决定了被加工零部件的加工精度（如尺寸、形状和相对位置）。五轴数控机床运动轴包括线性运动轴和回转运动轴两种形式，对于线性动轴而言，存在的空间六方位误差检测与辨识技术相对比较成熟，并且已经形成了系统的研究理论，以9线误差辨识法[7]、12线误差辨识法[8]、15线误差辨识法[9]、22线误差辨识法[10]为主；而对于回转轴空间六方位误差检测与辨识技术而言，国内外研究学者对此研究较少，且无系统性提升精度的研究理论，因此，针对数控机床回转轴空间六方位误差，深入研究了基本存在形式，采用空间几何数学分析法解析了回转轴间六方位误差的数学运算关系，并通过回转轴误差检测数据特征，提出适合性补偿方法，实现了回转轴滚转误差的精密补偿。

1 回转轴空间六方位误差形式

在三维空间中，任意回转轴回转运动过程中均会产生6项几何误差，包括：3项线性偏移位移误差和3项回转偏转误差。

如图1所示，以任意回转轴回转运动进行分析，令该回转轴中心线为Z轴，称该回转轴为C轴，其中，3项线性偏移误差分别表示为：δx(c)、δy(c)、δz(c)，3 项回转偏转误差分别表示为：εx(c)、εy(c)、εz(c)，回转轴空间六方位误差命名如表1所示，括号内字母c表示回转轴转动角度c，意为该误差是与回转轴转角c的关联函数。

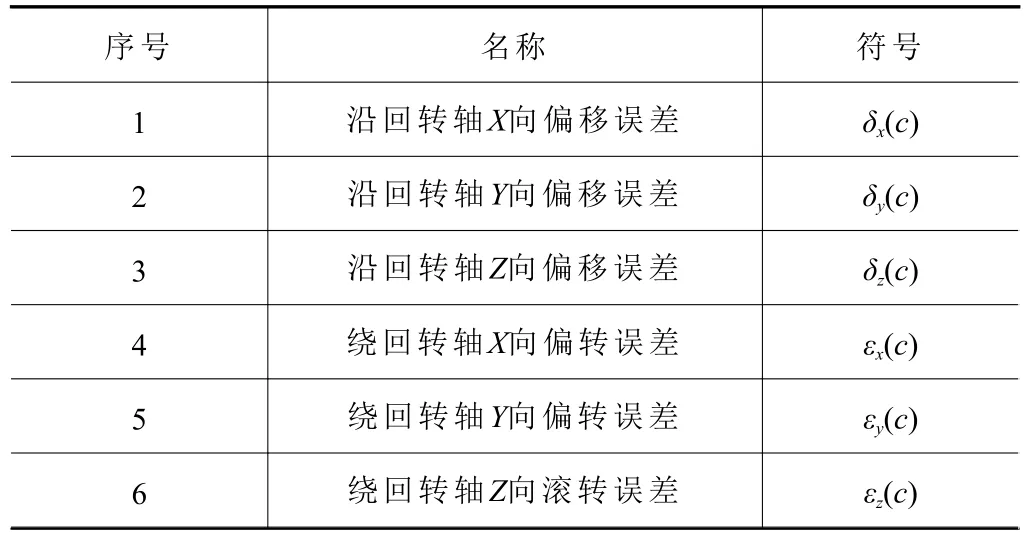
表1 回转轴空间六方位误差

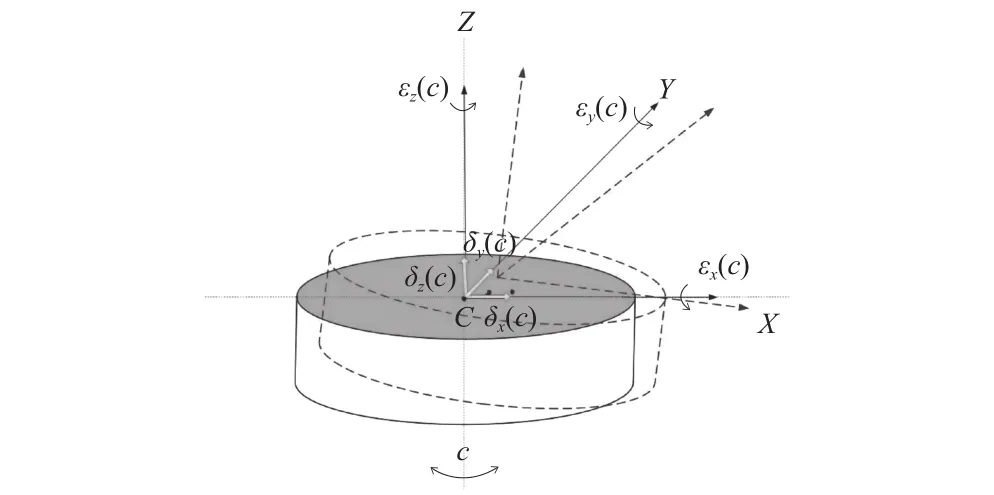
图1 回转轴空间六方位误差分布图

2 回转轴空间六方位误差辨识

准确辨识回转轴空间六方位误差是实现回转轴误差补偿及回转精度提升的必要手段，

2.1 沿回转轴 Z向偏移误差 δz(c)

如果通过检测实施直接得到回转轴中心位置轴向跳动量，则回转轴Z向偏移误差可直接得到，即：回转轴中心位置轴向跳动量为沿回转轴Z向偏移误差。

2.2 绕回转轴 X、Y向偏转误差 εx(c)、εy(c)

设置垂直回转轴C轴两个不同高度截面的检测面，分别检测截面X、Y向径向误差，可得到截面1的X、Y向径向误差为Δx1、Δy1，截面2的X、Y向径向误差为Δx2、Δy2，如图2所示。

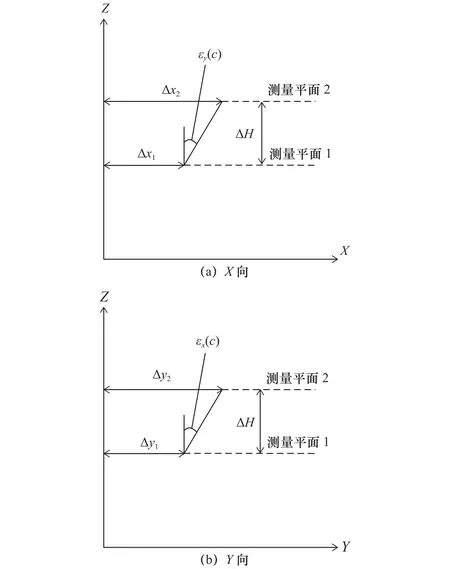
图2 不同截面径向误差测量简图

由图2几何关系，可列写式（1）、式（2）。

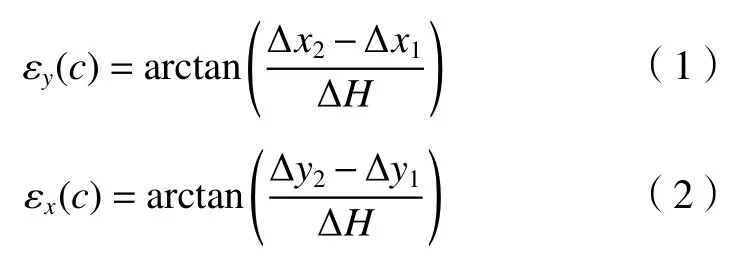
2.3 沿回转轴 X、Y向偏移误差 δx(c)、δy(c)

由误差来源分析知，回转轴C任意截面X、Y向径向误差，主要产生根源是由沿回转轴X、Y向偏移误差δx(c)、δy(c)和绕X、Y向偏转误差εx(c)、εy(c)间接产生，具体如图3所示。

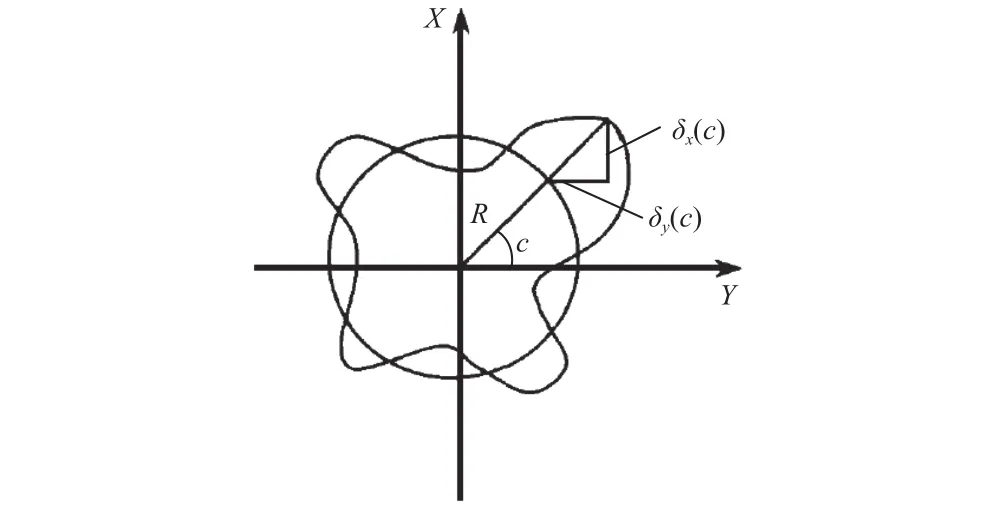
图3 偏移误差几何关系简图

联立图2、图3空间几何关系，可列写式（3）、式（4）。

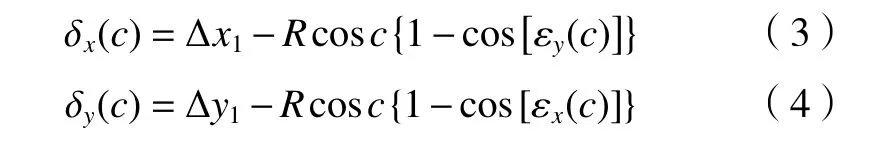
2.4 绕回转轴 Z向滚转误差 εz(c)

根据回转轴空间六方位误差元素分析，仅沿回转轴Z向偏移误差δz(c)对绕回转轴Z向滚转误差εz(c)没有影响，其余都会直接影响其大小。

假设，通过检测设备检测得到的回转轴回转误差为εc(c)，由其他5项误差因素引起的误差分别为εc1(c)、εc2(c)、εc3(c)、εc4(c)、εc5(c)，εz(c) =εc1(c)，εc1(c)为未受其他5项误差影响的真实绕回转轴Z向滚转误差，则有

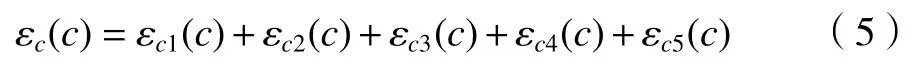
绕回转轴X向偏转误差εx(α) 引起绕回转误Z向滚转误差空间关系如图4所示，回转轴驱动转角为∠AOB，在实际驱动过程中，受绕回转轴X向偏转误差εx(α)的影响，目标点B转至点D，过点D作XOY面垂线，E为垂点，过点D向OX做垂线，C为垂点，则可以得到，实际滚转误差为∠AOE，εx(c)=∠BCD，εc2(c)=∠EOB，CB=CD。

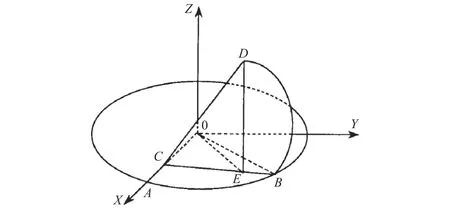
图4 绕X向偏转误差与滚转误差关系图

由空间几何关系知，在ΔBOC中，可列写式（6）～（8）。

在ΔCED中，可列

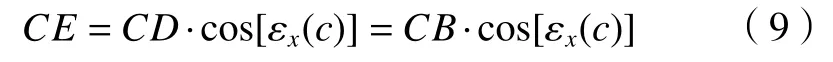
将上述推理式（6）～（8）代入式（9）中，可以整理得

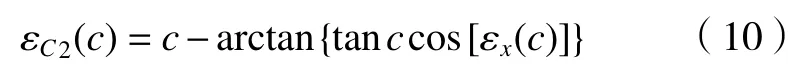
式（10）所求解εC2(c)为绕回转轴X向偏转误差εx(c)引起的回转误差。

根据上述空间几何关系，可同理得到，绕回转轴Y向偏转误差εy(c)引起的回转误差为式（11）的解εc3(c)。

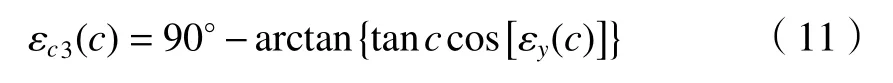
沿回转轴X向偏移误差δx(c)引起回转轴滚转误差空间几何关系如图5所示，回转轴驱动转角为∠AOB，在实际驱动过程中，受沿回转轴X向偏移误差δx(c)的影响，使驱动目标点B移至空间点D，且BD=δx(c)，过点D作垂线垂直于Y轴，交点为C，实际滚转误差为∠AOD，∠DOB=εc4(c)，由于OA连线与DC连线平行，所以得出∠ODC=∠AOD。

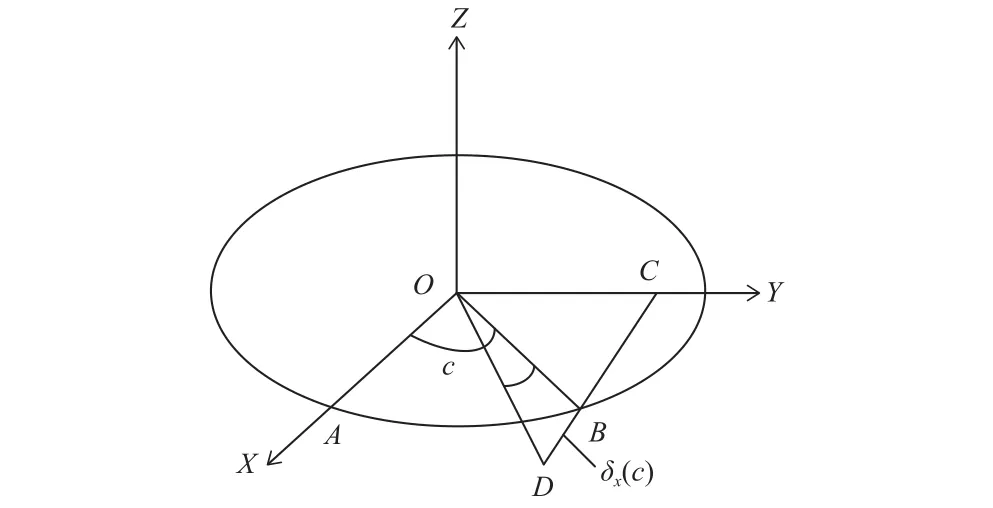
图5 沿X向偏移误差与滚转误差关系图

由图5空间几何关系，可列

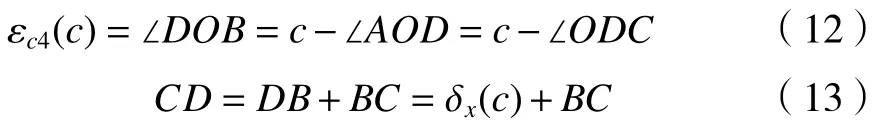
在ΔCOD中，可列

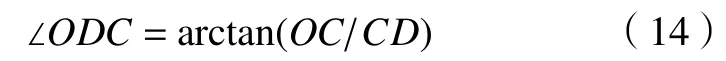
在ΔOBC中，可列

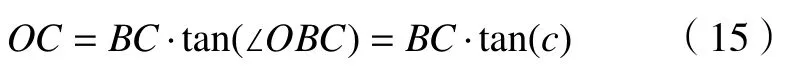
将上述式（12）～（14）代入式（15）中，可以整理得

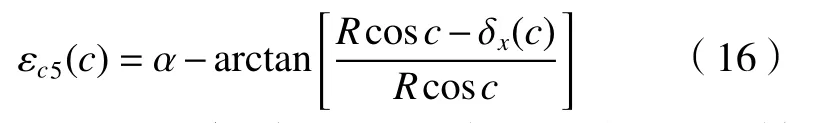
根据上述空间几何关系，可同理得到，沿回转轴Y向偏转误差δx(c)引起的回转误差为式（17）的解εc5(α)。

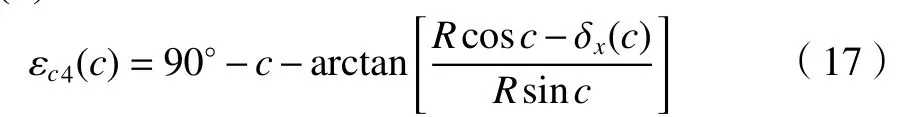
综上空间几何关系解析，将式（10）、（11）、（16）、（17）代入式（5）中，可得到回转轴绕Z向滚转误差εz(c)的大小为式（18）所示。

式（18）的解εz(c)即为为绕回转轴Z向滚动误差。

3 回转轴转角误差检测

采用XL-80型激光双频干涉仪角度检测组件对回转轴滚转误差进行检测，选用ALAR-100-sp回转轴出厂的沿回转轴X向偏移误差和沿回转轴Y向偏移误差为参考数据，进行该回转轴转角误差检测，检测现场如图6所示。

图6 检测现场

设置回转轴每转动5°进行滚转误差检测，回转轴与检测设备在每个检测点停留4 s进行误差采集及传输，以5次检测取均值为滚转误差数据，如表2所示。

由表2滚转误差数据分析知：回转轴滚转误差随着旋转角度变化，大小一直处于近似递增特性，仅在第三段（-50°，-40°）内略有减少，最大增量14.506 arcsec在（10°，20°）出现，最大增值 93.688 arcsec 在（70°，80°）出现。

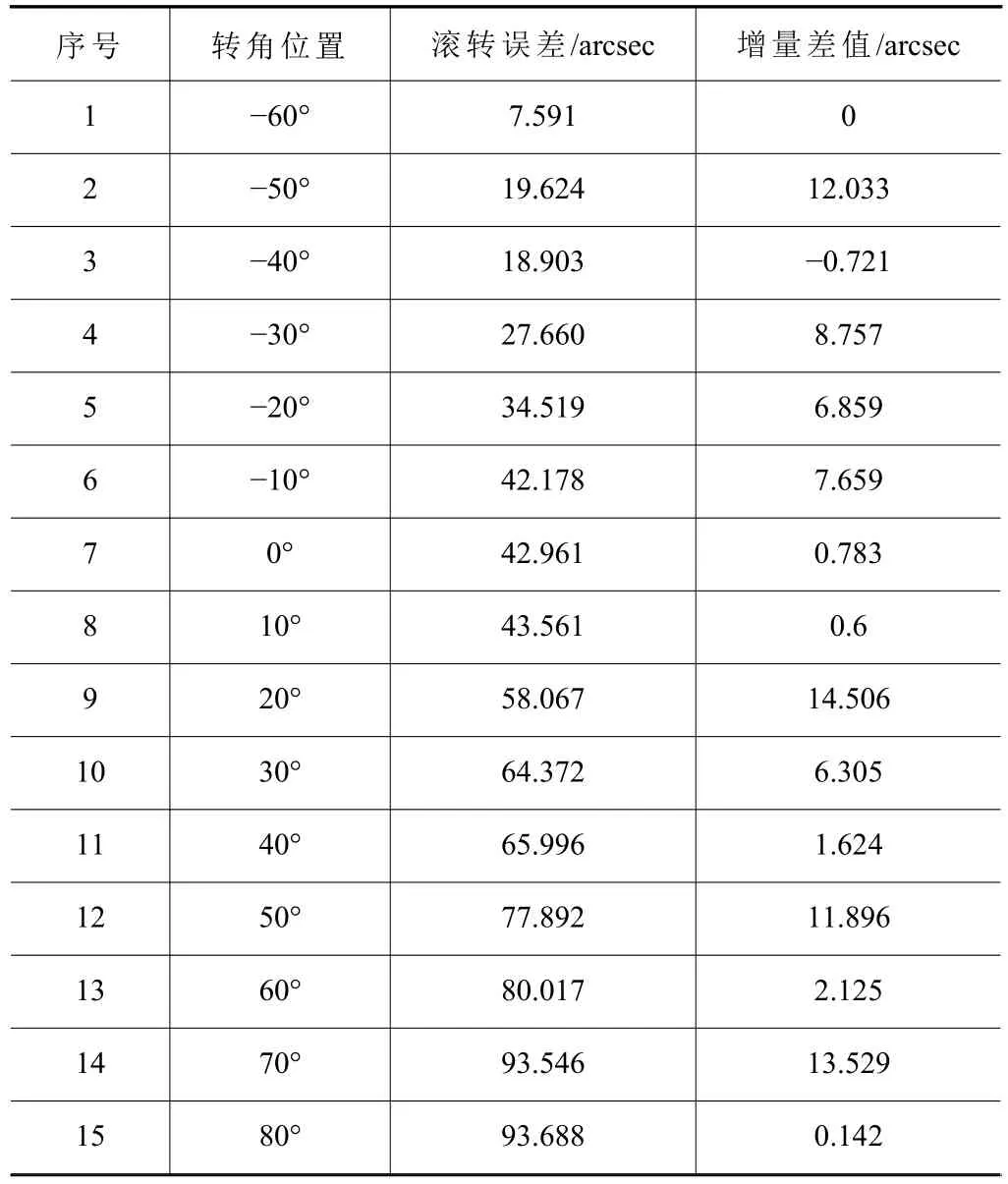
表2 误差检测数据

4 适应性误差补偿

以该回转轴滚转误差具有的累积递增特性，提出适应性补偿原理，具体实施如下：

4.1 创建累积性数据库

将回转轴摆角位置进行λ等分，利用XL-80角度检测组件对节点位置P滚转误差进行检测和累计值ε云保存，称为数据库，如式（19）所示。

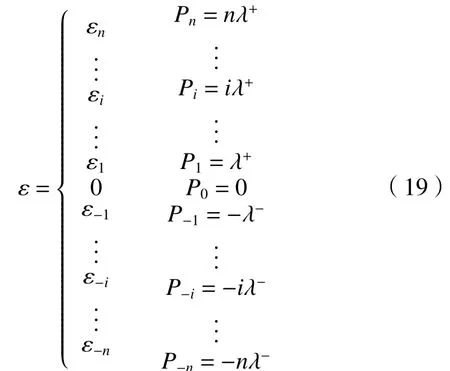
4.2 建立补偿模型

创建适应性前馈系统，内部为滚转误差补偿模型，当回转驱动器输出转动指令后，指令经前馈系统进行运算处理，解算得到无滚转误差驱动指令。

补偿模型以当前位置P(光栅反馈)和转动角度θ(驱动发出)为自变量，经前馈运算后输出为转动角度θ和滚转误差ε′的叠加θ′=θ-ε′。模型构建步骤如下：

4.2.1 建立滚转误差逼近方程

应用直线方程两点直线法建立从回转轴零点至正极限直线方程，如算式（20）所示。

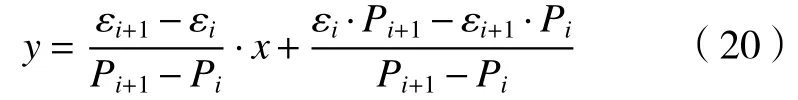
同理，应用直线方程两点直线法建立从回转轴零点至负极限直线方程，如式（21）所示。

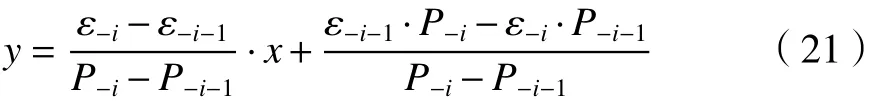
式中：Pi、εi为零点至正极限位置和滚转误差；P-i、ε-i为零点至负极限位置和滚转误差。

4.2.2 解算位置Pa、转动角度θ滚转误差ε′

根据当前转动位置Pa和目标转动位置Pb大小，补偿模型分为4种形式进行补偿：

（1）Pa∈(0,Pn)，Pb∈(0,Pn)

假 设 ，0≤i＜j≤n，Pi≤Pa≤Pi+1，Pj≤Pb≤Pj+1，利用逼近方程算式（20），可解算位置Pa、Pb的滚转误差εa和εb，算式关系如（22）、（23）所示。

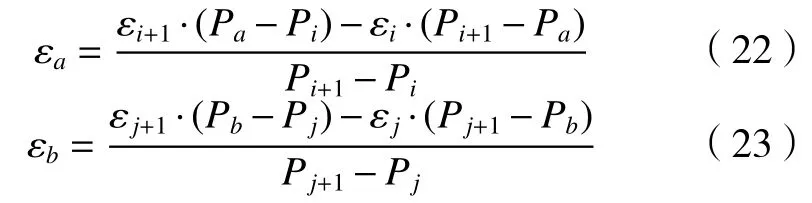
通过算式（22）、（23）可解得对应该位置转动角度θ的滚转误差ε′为

整理可得滚转误差ε′如式（25）所示。

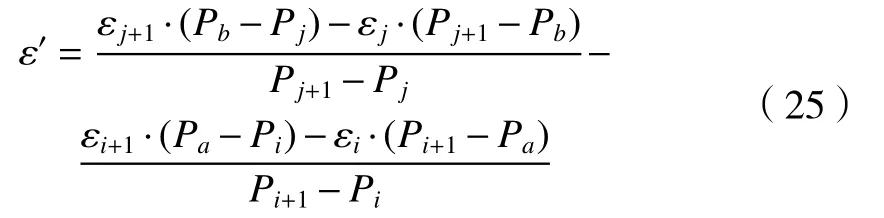
（2）Pa∈(0,Pn)，Pb∈(P-n,0)

假 设 ，Pi≤Pa≤Pi+1，P-j-1≤Pb≤P-j， 利 用 逼 近方程式（20）、（21），可解算位置Pa、Pb的滚转误差εa和εb，算式关系如式（26）、（27）所示。

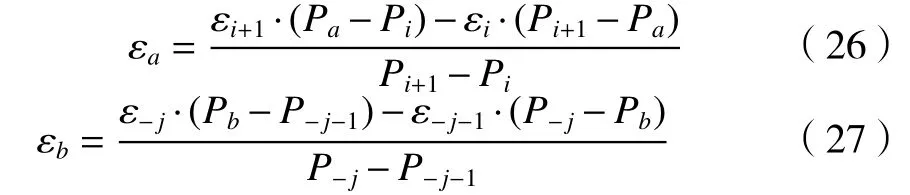
通过式（26）、（27）可解得对应该位置转动角度θ的滚转误差ε′为

整理可得滚转误差ε′如式（29）所示。

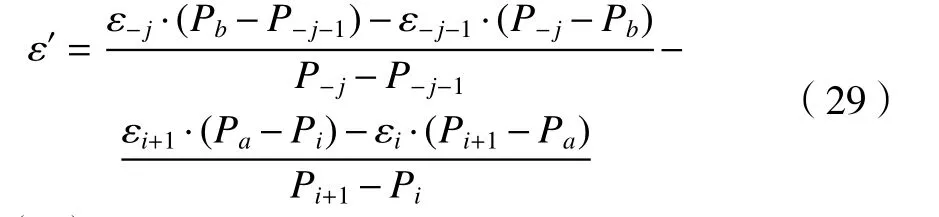
（3）Pa∈(P-n,0)，Pb∈(0,Pn)

假 设 ，P-i-1≤Pa≤P-i，Pj≤Pb≤Pj+1， 利 用 逼 近方程式（20）、（21），可解算位置Pa、Pb的滚转误差εa和εb，算式关系如式（30）、（31）所示。

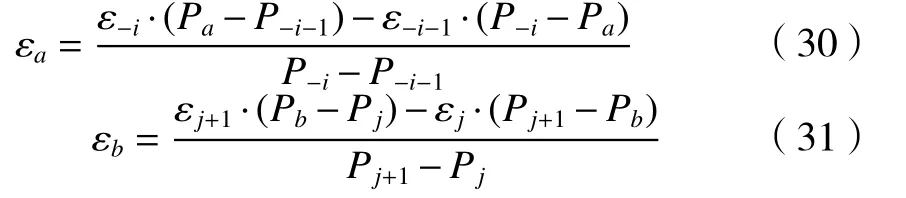
通过式（30）、（31）可解得对应该位置转动角度θ的滚转误差ε′

整理可得式（33）。

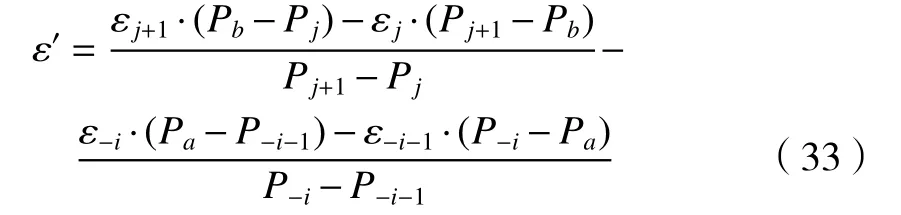
（4）Pa∈(P-n,0)，Pb∈(P-n,0)

假设，P-i-1≤Pa≤P-i，P-j-1≤Pb≤P-j，利用逼近方程式（21），可解算位置Pa、Pb的滚转误差εa和εb，算式关系如式（34）、（35）所示。

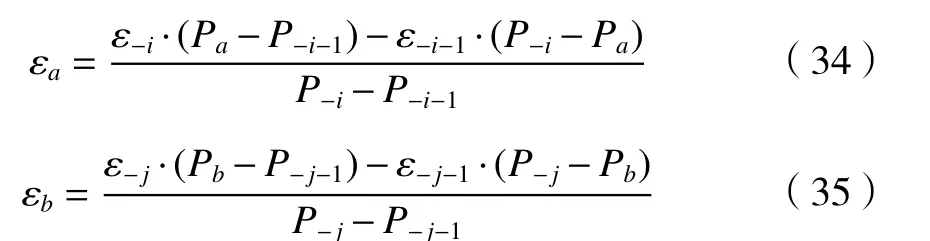
通过式（34）、（35）可解得对应该位置转动角度θ的滚转误差ε′为

整理可得滚转误差ε′如式（37）所示。

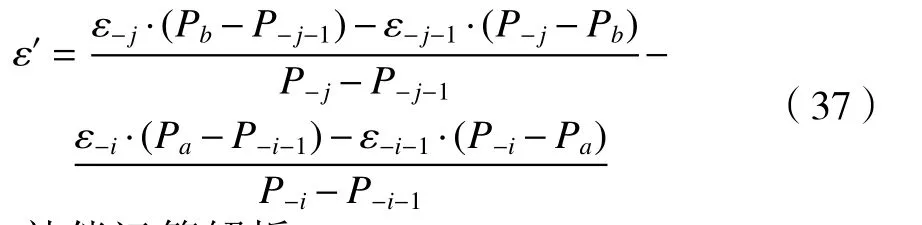
4.2.3 补偿运算解析

用方程关系解算得到的滚转误差ε′对初始位置Pa、转动角度θ、目标位置Pb实施补偿，解析得到补偿后转动角度θ″运算关系如式（38）所示。

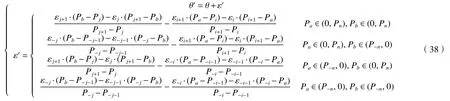
5 实验分析

对回转轴C空间六方位转角误差进行辨识和适应性补偿实验，补偿模型参数如表3所示。

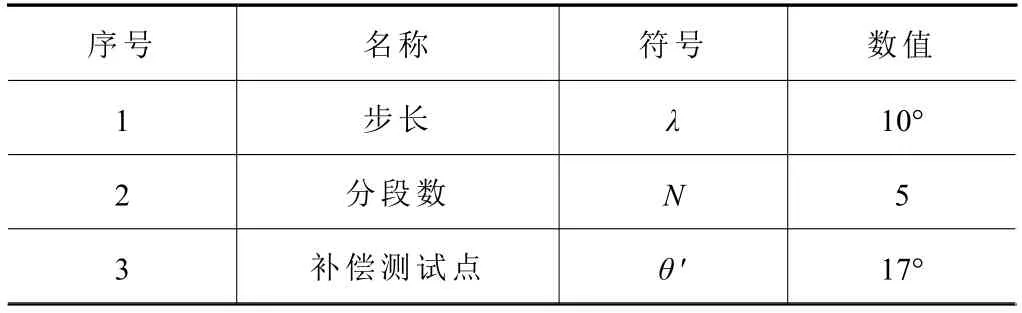
表3 补偿模型及实验参数

为直观表明补偿前后滚转误差分布，应用Matlab对滚转误差数据进行拟合，如图7所示。

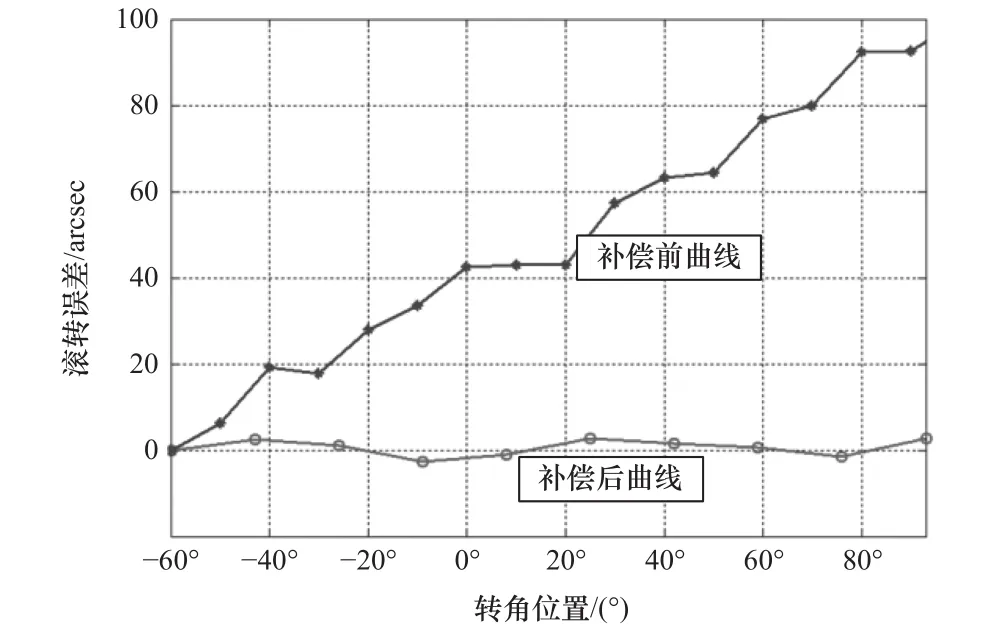
图7 补偿前后对比

由图7曲线分析知：回转轴C轴经适应性补偿后，回转轴C轴滚转误差显著减小，且适应性补偿后滚转误差曲线在零线波动，通过计算得到补偿后残差最大值、残差均值和残差均方差如表4所示。

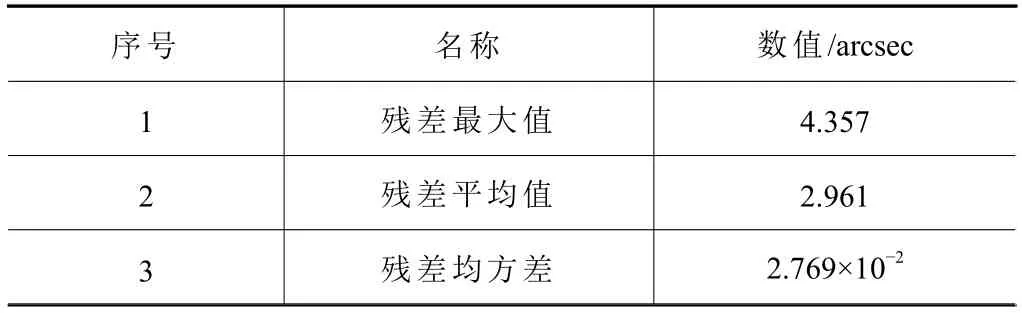
表4 补偿后残差数据

由表4残差数据进一步表明，研究的空间六方位转角误差辨识及适应性补偿方法可以有效降低回转轴滚转误差。

6 结语

针对回转轴空间六方位误差进行了数学解析和补偿实验，得出以下结论：

（1）回转轴运动过程中空间六方位误差大小数值存在相互影响关系，用数学基础理论可以对回转轴空间六方位误差进行具体的解析建模；采用成熟的检测设备“激光双频干涉仪XL-80角度检测组件”可以实现回转轴滚转误差的检测与辨识。

（2）根据被测回转轴滚转误差具有的增减特征，提出适应性补偿方法，建立具体的补偿数模，经实验表明，研究的回转轴空间六方位误差辨识及补偿理论可靠实用，补偿后滚转误差残差均数据得到明显降低，可满足高精度五轴数控机床的运动需求。

（3）针对适应性补偿模型，运行参数等分步长λ和分段数N,如果对其进行进一步精细设置，该模型针对滚转误差具有增减特征的回转轴来说，补偿精度将得到显著提升。