通过分离直线确定参数的取值范围

四川省绵阳市开元中学(621000) 敬加义 余胜蓝

英国纽卡斯尔大学自动化学院(NE17RU) 敬铠临

在高考和各地的模考试题中,确定方程或不等式中参数的取值范围常常是该套试卷的压轴题,其解法基本是分类讨论法或分离常数法,这些解法对考生的综合数学能力要求很高,许多考生难得高分. 本文通过分离直线,将问题转化为函数图像研究,通过数形结合,利用直线的斜率k和y轴上截距的几何意义,化归为特定的直线与曲线位置关系,达到确定参数取值范围之目的,从而也达到降低难度的效果. 通过教学实践,效果不错.

一、化归为y =kx 型

例1 (2022 年金太阳高三联考理科卷) 已知函数f(x)=x+aln(x+b)的图像经过坐标原点,且a ＜0.

图1

例2 (2019 年高考全国Ⅰ卷文科) 已知函数f(x) =2 sⅰnx-xcosx-x,f′(x)为f(x)的导数.

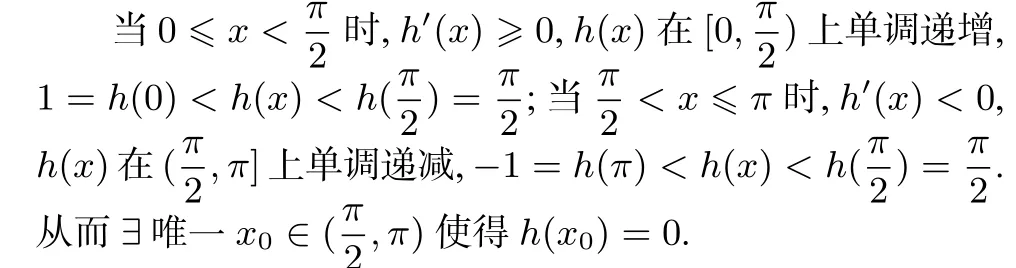
当x ∈[0,x0)时,h(x) ≥0;当x ∈(x0,π]时,h(x) ≤0.所以g(x) 在[0,x0) 单 调递增, 在(x0,π] 上单调递 减,g(x)max=g(x0) = 2 sⅰnx0-x0cosx0,g(0) = 0,g(π) =π.作出g(x) 图像如图2. 其中P(π,π), 线段OP的方程y=x(x ∈[0,π]),l在阴影区域内,kl≤kOP,即a+1 ≤1,所以a≤0. 故a的取值范围是(-∞,0].

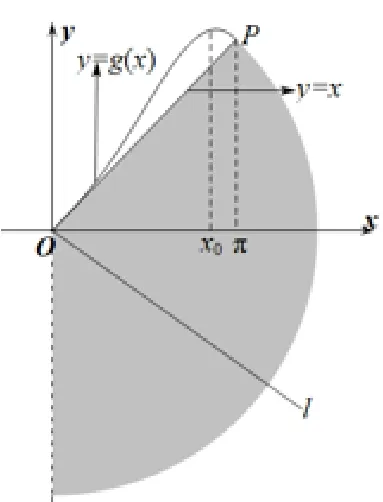
图2

二、化归为y =k(x+x0)型

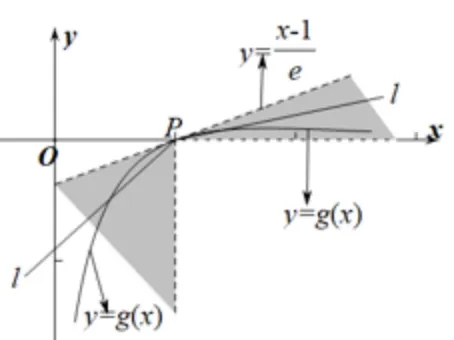
图3

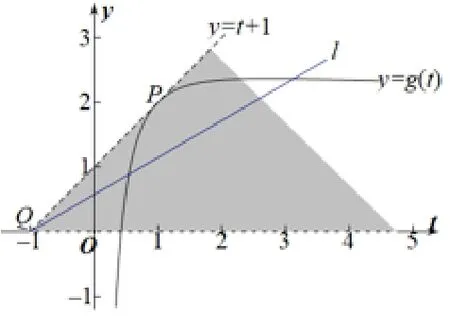
图4

例4 (2017 年高考全国Ⅰ卷理科) 已知函数f(x) =ae2x+(a-2)ex-x.

(1)讨论f(x)的单调性;

(2)若f(x)有两个零点,求a的取值范围.

三、化归为y =kx+b 型

例5 (2021 年高考海南卷)已知函数f(x) =aex-1-lnx+lna.

(1)当a= e 时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;

(2)若f(x)≥1,求a的取值范围.

解 (1)略;(2)

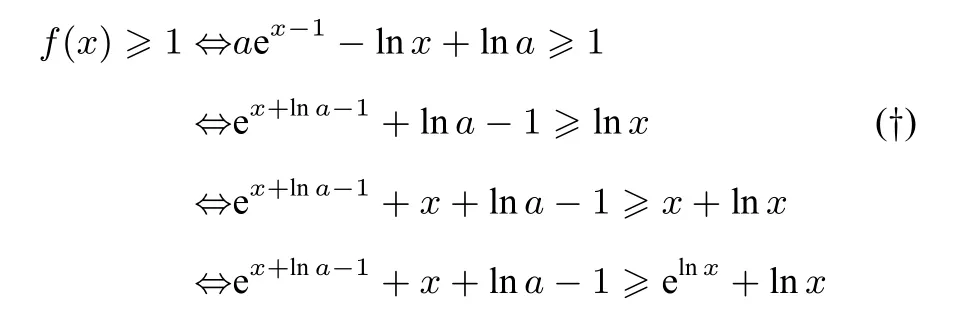
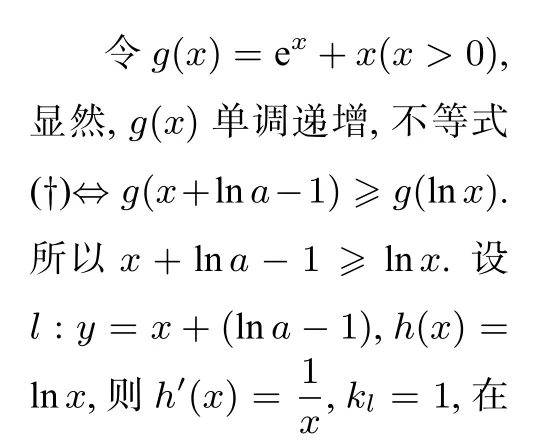
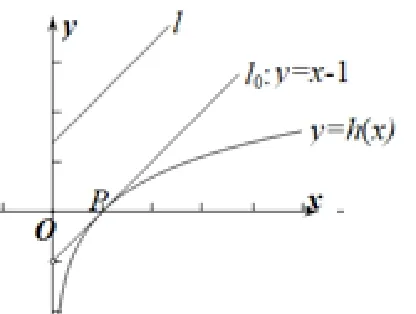
图5

例6 (2021 年浙江模拟卷)已知函数f(x)=e2x-(a+2)x,a ∈R.

(Ⅰ)讨论函数f(x)的单调性;

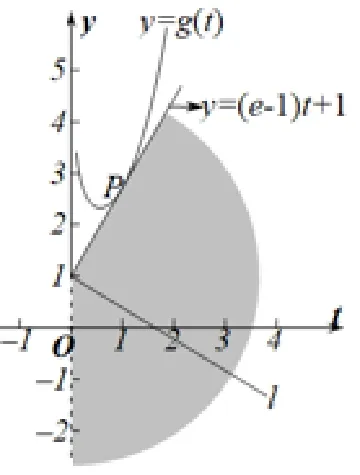
图6

四、化归为y =k(x+x0)+y0 型

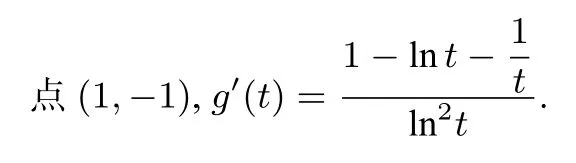
图7

(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值;

(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,证明:e-2＜a ＜1.

解 (1) 略; (2) 证明: 因f(0) =f(1) = 0,函数f(x)在区间(0,1) 内有零点, 则函数f(x)在区间(0,1)内至少有三个单调区间,所以g(x) =f′(x)在(0,1) 上应有两个不同的零点.

图8

由f(1)=0⇒e-a-b-1 = 0⇒b= e-a-1, 因此,g(x) =f′(x) = ex-2ax-b= ex-2ax-e+a+1,所以f′(x)=0,即ex-2ax-e+a+1=0,也即方程