圆锥曲线一类直线定向定点性质的完整结论
2022-08-30山东省邹平双语学校256200姜坤崇
中学数学研究(广东) 2022年15期
山东省邹平双语学校(256200) 姜坤崇
问题 过圆锥曲线(椭圆、双曲线、抛物线)上一定点P引两条斜率之和(积) 为常数的直线分别交曲线于另一点A,B,那么直线AB有怎样确定的性质呢?

证明 (Ⅰ)当y0=0 时,如图1,点P为E的左(或右)顶点,由椭圆及两直线PA,PB关于x轴对称知直线AB垂直于x轴(有定方向).

图1

图2





(Ⅰ)求C的方程;
(ⅠⅠ)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足. 证明: 存在定点Q,使得|DQ|为定值.的斜率是非零常数.
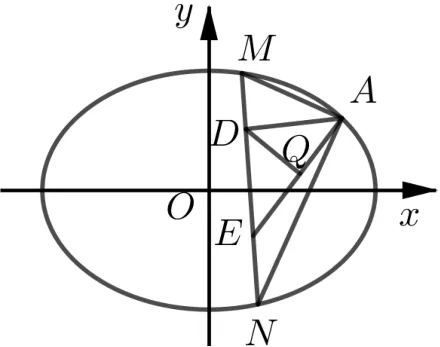
图3



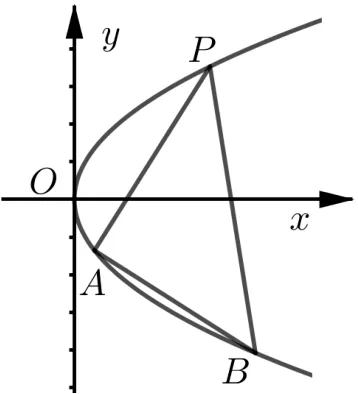
图4


由以上探讨,可得一般性结论为: 过圆锥曲线(椭圆、双曲线、抛物线)上一定点P引两条斜率之和(积)为常数的直线分别交圆锥曲线于另一点A,B,则直线AB有定方向或过一定点.
