三进制数码在数列题中的应用

华南师范大学数学科学学院(510631) 刘 倩

早在小学教学中,教师在教授学生“满十进一”的规则时就会告诉学生世界上不是只有十进制这一种计数方式. 在中国古代有六十四卦卜易规则用到二进制计数思想[1];1 个季度有3 个月,这是运用三进制计数思想;1 斤是16 两(中国古代度量法),这是运用十六进制计数思想;1 天有24 小时,这是运用二十四进制计数思想;1 个小时60 分钟、1 分钟有60秒,这是运用六十进制计数思想……

每一种进制都是完美的,这样完美的数学工具应为学生所知. 横观人们研究十进制数的进程,数码问题是其中十分重要的模块,并由此衍生出不少数列问题. 那么,其它进制应有对应的数码规律,可以衍生出对应的数列问题. 本文从最能反映真相的三进制入手,研究三进制数码规律,并探究对应的数列问题,仿照三进制数码研究过程,参照十进制数码知识推测P进制数码规律.

一、理论探究

一个正整数的三进制表示是n=ak3k+ak-13k-1+···+a131+a0,其中ak=1,2 且am=0,1,2(0 ≤m≤k-1).以下研究[3k-1,3k-1](k ∈N+)[注1] 中正整数用三进制表示后三进制数的数码知识,即k(k≥1)位三进制数的数码知识.

二、例题分析

由表2.1 可知当数的三进制表示中包含0 时就不满足条件f(n) =n,问题转化为1～1991 有多少数的三进制表示是不含0 的,这样也就定义了三进制去0 数列问题. 1991 写作三进制数是(2201202)3. 那么有两种思路: 第一种方式是考虑1～6 位以及7 位中小于(2201202)3且包含0 的数码个数;第二种是考虑1～6 位以及7 位中小于(2201202)3只含1 和2 的三进制数.

表2.1 问题1 部分值

按第一种方式可得算式:

解析 首先需要知道题给的条件使得数列下标和数列值之间有什么样的联系,列举一部分值在表2.2 中.

表2.2 问题2 部分值

三、实战演练

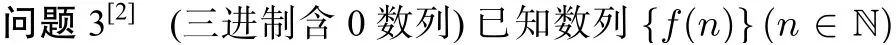
解析 要得到题设的结果,首先找出什么条件可以达到这个结果,依旧先列举一部分值,观察规律.

表3.1 问题3 部分值

四、总结

数列问题是高考必考题,简单的题是只考察数列本身如等差、等比数列基本知识,中档往上的题目大多是考察学生的综合知识,包含许多学生容易忽略的数学知识的综合,比如数列与函数,数列与几何的综合. 事实上,进制问题本身就是其中冷门却值得学习的一类.

在三进制数列数码知识的研究过程中,不难发现此中涉及了组合恒等式、等差数列、等比数列、解方程的多方面知识,从理论到问题都体现着数学逻辑的重要性,在这些理论知识的学习中,学生的推理能力、逻辑思维能力、计算能力都能得到锻炼,所掌握的数学知识也更为完整. 更值得关注的是三进制和实变函数中Cantor 集有千丝万缕的联系[3],这就将高等知识和中学知识进行结合,以高等知识指导中学问题,更能提升学生对数学学科的理解.