针对特殊威胁的改进人工势场法航迹规划

2022-08-30李红烨

探测与控制学报 2022年4期

李昱，李红烨

(中国舰船研究院，北京 100083)

0 引言

无人机(UAV)全称为“无人驾驶飞机”或“无人自主飞行器”，是一种依靠无线电遥控或者机载程序自动控制的不载人飞行器。无人机广泛应用于民用领域与军事领域，可执行航拍、测绘、通信中继、目标侦察打击等多种任务。与载人飞机相比，其优势在于更高的全天候工作能力，更低的资源消耗，其更适用于简单重复性任务以及高风险任务。无人机执行任务的回报率更高，任务失败的代价损失更小。目前各国都将装备发展的核心转移到无人装备领域中，其中，无人航行器是无人装备的重点研究对象[1-2]。

无人机在执行任务前或执行任务过程中需要对其航行路线进行规划。航迹规划主要是指使用相关算法实现无人机自动导航的功能，是人工智能及导航与制导领域中的重要研究方向之一。对于一般的无人机，在执行任务前，会根据战场已知信息(如目的地、任务区域、威胁区域等)对无人机的飞行路线进行设置，实现无人机独立自主工作；对于功能更加复杂的无人机，其可以使用机载传感器等自主判别风险事态并执行自主规避、创建新航迹等动作。无人机航迹规划的基本原则是在保证自身安全的前提下实现路径最短、效率最大化，即“最优路线规划原则”。航迹规划对于无人机执行任务有着至关重要的作用，其重点讨论的问题在于航迹规划算法的构建与优化，使无人机利用最少的资源计算得出最优的路径[3-4]。

目前已有多种成熟的航迹规划算法，传统的确定性方法包括智能搜索算法、最速下降法、可视图方法、人工势场法、单元分解法、最优控制方法、模拟退火算法等。现代智能航迹规划算法有随机化航迹搜索方法以及结合遗传算法、蚁群算法、神经网络算法发展而来的子算法等。

本文所研究的人工势场法为传统算法中的经典算法之一，其优势在于算法的理论简洁易懂，算法的建模方案以及计算过程相对简单，计算开销相对较小。但是传统的人工势场算法适用范围较小，在不加以优化的前提下，只能对单一威胁源执行规避。在实际战场应用中，飞行器的航线上很可能存在多个敌方威胁需要规避，甚至存在一整个区域需要规避的情况；同时传统APF算法由于其理论、方法本身固有的缺陷存在区域极值的问题，导致规划出的航迹存在尖点以及振荡等问题。因此，传统APF算法必须加以改进才能得以适用[5-7]。

在对传统算法的改进过程中，主要以无人机的特殊威胁作为任务背景，综合考虑了障碍物建模、引力斥力的产生方式和飞行器的最大转角等问题，建立改进后的人工势场法数学模式，并在Matlab软件中进行仿真计算，再通过与传统算法生成的路径相比较验证算法的改进效果。

1 传统人工势场法

1.1 算法的概念及原理

传统人工势场法的基本思想是在空间中人为构造出一个虚拟的势场。这个虚拟的势场由两部分组成：第一部分是一个由目标点产生的引力场引导物体向其运动；第二部分是一个由障碍物产生的斥力场，避免航行器与障碍物发生碰撞。通过查找势场函数下降的方位来得到最优的路径，物体在路径上每一点所受的合力等于这一点所受到的斥力和引力的矢量总和。这里的关键是如何构建引力场和斥力场[8-9]。我们将引力场写作Uatt，斥力场写作Urep，两个势场的总势场即为矢量相加：

U=Uatt+Urep。

(1)

总势场如图1所示。

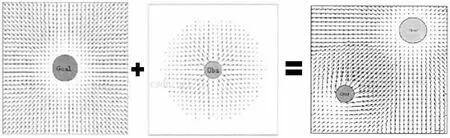
图1 总势场Fig.1 Total potential field

定义引力Fatt为引力场的负梯度，斥力Frep为斥力场的负梯度，无人机受到的合力即为引力与斥力的矢量和，如图2所示。

Fatt=-∇Uatt，

(2)

Frep=-∇Urep，

(3)

Ftotal=Fatt+Frep=-∇Utotal=-∇(Uatt+Urep)。

(4)

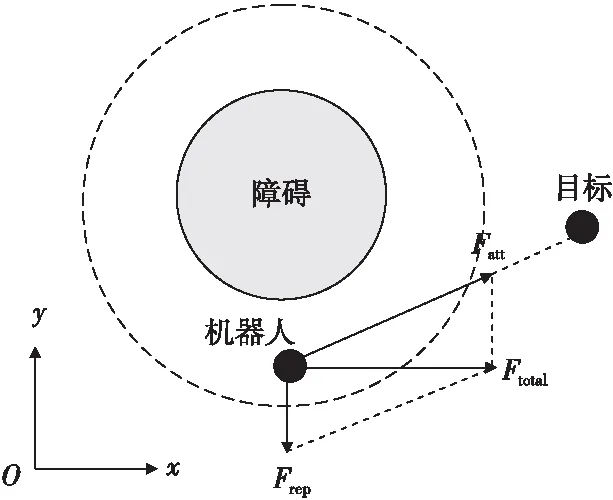
图2 机器人受力图示Fig.2 Force diagram

引力场与引力：设X是当前无人机的位置，Xg是目标点的位置，X-Xg为目标点与无人机之间的距离，Katt为引力场的增益系数。则无人机与目标点之间的引力场

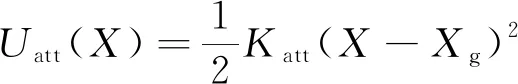
(3)

无人机在该力场中所受的引力为该力场函数的负梯度，即

Fatt(X)=-∇Uatt(X)=-Katt|X-Xg|。

(4)

该引力的特点是在起始点处无人机受引力最大，且随着无人机与目标点距离的减小而线性趋近于0[10-11]。

斥力场与斥力：设X是当前无人机的位置，Xobs是障碍物的位置，X-Xobs为障碍物与无人机之间的距离，ρ0是无人机受障碍物的影响距离，krep是斥力的增益系数。则无人机与障碍物之间的斥力场

。

(5)

该力场函数的特点是其产生的势能与无人机和障碍物之间的距离有关，势能随着无人机和障碍物之间的距离增加而减小，与距离成反比。该力场函数为分段函数，在障碍物的影响距离之外可以认为不受障碍物的作用，在障碍物的点上可以认为其值无穷大。

无人机在该力场中所受的斥力为该力场函数的负梯度，即

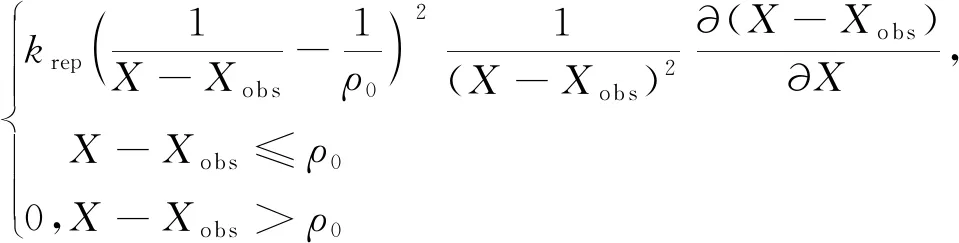
(6)

对于多个障碍物所形成的势场可以利用势场的叠加原理将多个势场矢量相加以得到总势场

Utotal=Uatt+∑iUrepi。

(7)

所受合力为总势场的负梯度[12-13]

Ftotal=Fatt+∑iFrepi。

(8)

1.2 算法的Matlab实现

传统APF算法的Matlab程序主要包含四个部分：分别是程序主体，用于定义初始变量；调用函数，进行循环计算路径点以及画图；三个子函数，分别是引力计算、斥力计算以及引力与斥力的角度计算函数。

在程序中需定义如下变量：起点终点障碍物位置坐标、引力增益系数、斥力增益系数、障碍影响距离、障碍个数、障碍半径、步长、循环次数等初始值。初值设定完成后进入循环阶段，每次循环通过计算引力、斥力的合力方向来确定无人机的下一步运动方向，再根据步长来决定无人机下一步的位置，即为一次循环。通过增加循环次数来确保无人机能够到达目标点。

角度计算函数的输入有无人机的坐标、目标和障碍物的坐标以及障碍物的个数。其目的是计算出无人机与目标点以及各障碍物之间的夹角以便于在计算引力和斥力的函数中使用来计算引力和斥力的各个分量。

引力计算函数的输入有无人机的坐标、目标和障碍物的坐标、障碍物的个数、引力增益系数和引力与X轴正方向夹角。其目的是得到引力的X方向和Y方向的两个分量以便于主体函数中矢量相加求得合力[14]。

斥力计算函数的输入有无人机的坐标、目标和障碍物的坐标、障碍物的个数、斥力增益系数、斥力与X轴正方向夹角和障碍物的影响范围。其目的是计算出各个障碍物对无人机的斥力的分量

子函数输出值最后通过导入主程序进行循环计算并绘制出航迹的实际路线[15-16]。

2 特殊威胁的人工势场算法建模过程

2.1 特殊威胁的定义

对于传统的APF算法来说，其对传统威胁的定义为从A至B航线上的一个威胁点，当所需要避开的威胁不能简化为单一点坐标时，传统的APF算法将无法适用[17]。

我们将除传统APF算法适用的单一威胁源以外的其他形式威胁称作特殊威胁，其包括航迹路线上需要规避的多个简化后的点威胁、平面区域威胁以及空间区域威胁等。

本文研究的重点在平面上的面区域威胁，多点威胁可直接使用该研究算法进行简化，空间立体区域可做相关拓展得出更进一步的结论。在面区域威胁的研究上，我们更关注障碍物的形状、顶点以及其边缘轮廓等特征。对于无人机的一条最优航迹来说，既要避开障碍物所占区域，又要尽可能贴近其边缘，实现安全性与效率最大化[18]。

本文研究的“特殊威胁”背景如下：我方无人机执行任务需从起点A飞往终点B，原计划按照最短路线，即AB连接直线飞行；同时在飞行器起飞前由战场侦察反馈信息发现在原计划飞行区域上可能存在敌方的防空火力覆盖，进而须重新计算航迹路线避免被敌方击落；重新计算航迹的过程可在地面进行计算并将新的航迹路线上传至飞行器导航系统中或直接将测得的关键数据上传给飞行器，由机载计算机中的算法直接计算得出新的航迹。所需的关键数据有：起点与目标终点位置信息，威胁区域的边界信息等。改进算法将自动计算航路是否重叠，是否需要规避，如何有效规避等任务，并自动设计出一条安全有效的新航路进行导航[19]。

2.2 特殊威胁区域的拟合优化

通常威胁区域为不规则图形，对不规则图形进行合理的拟合化为规则的多边形区域以方便算法的设计与计算。当输入为已知某一威胁区域的边界点坐标时(如图3中多个点坐标)，改进算法可以自动判断出距离起点最近的坐标并且由此连接相邻点坐标，进而绘制出威胁多边形区域。如图3所示，当已知边界点坐标A、B、C、D时，算法可以自动计算并拟合出简化后的威胁区域，进而执行下一步的处理工作。

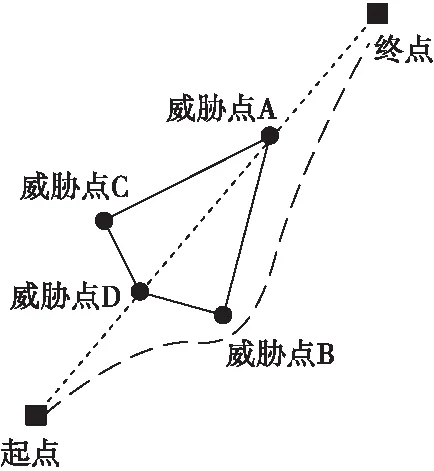
图3 威胁区域的拟合优化Fig.3 The optimization of threat aera

当威胁区域边界点坐标组成的威胁区域为凹多边形时，算法在计算多边形区域时会出现多种凹多边形的情况无法确认，进而导致算法中止。

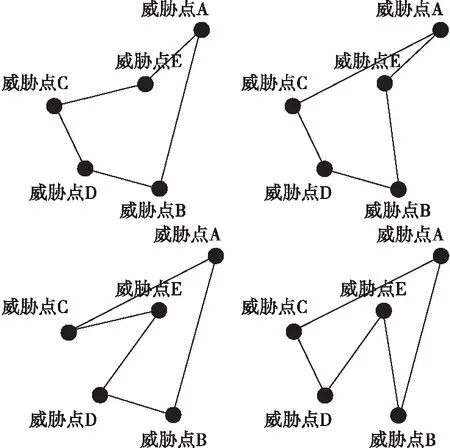
图4 多种凹多边形区域情况Fig.4 Multiple cases of threat regions

如图4所示，当凸多边形内部存在威胁点坐标进而组成凹多边形时，会出现多种多边形威胁区域的情况，算法无法自主确认具体威胁区域，进而需要对该种情况进行分类讨论。最简单的办法即忽略掉该内部的边界点，将威胁区域扩大为凸多边形。虽对原始威胁区域有一定的扩大，但可减少多个判断识别的步骤，节约大量的计算。

如图5，将内部威胁点忽略进而组成优化后的凸多边形区域。原始航迹如图短虚线，目标的规避航迹如图长虚线。如增加威胁区域边界条件至更多点或线的集合，亦可根据上述思路得到相应的凸多边形作为优化后的规避区域[20-21]。

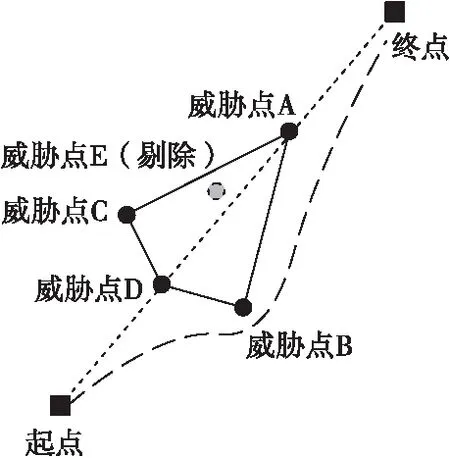
图5 去除内部威胁点的拟合优化Fig.5 The optimization of threat aera after removing internal threat point

2.3 改进算法设计原理

传统人工势场算法认为无人机航行中每一个时间点所受到的合力是根据目标点产生的引力和障碍点产生的斥力共同决定的。在本文中，目标点依然为单一的坐标点未发生变化，因此引力模型可以沿用传统人工势场法中已有的结论。对于斥力来说，原有的障碍点变为障碍区域，模型将有所变化，这也是改进算法的重点研究部分。

平面上的凸多边形的每条边的延长线可以将整个平面分割成多个部分，如图6为四个威胁点的平面化分情况。

假如起点设为左下角(0，0)点附近，终点设为右上角(100， 100)点附近，可以发现若无人机以直线路线从起点向终点飞行的话将经过威胁区域正上方，因此需要采取手段从两侧规避；在无人机经过区域2，4，6，8(即威胁区域多边形的边对应区域)以及区域9，10(延长线相交后的区域)时，我们认为可让无人机贴近区域边界并与边界保持一定距离前进效率最高；在无人机经过区域1，3，5，7(即威胁区域多边形的顶点对应区域)时，我们认为此时无人机需要进行平滑的转向远离区域11(威胁区域)。

综上我们将平面中所有被划分的区域分为三大类：1) 顶点对应区域需要平滑转向；2) 边对应区域可贴近前进；3) 威胁区域不可跨越。

如图7所示，根据两种非威胁区域的类型制定两种对应的障碍点选取规则。当无人机经过顶点对应区域时，我们将算法中的威胁点设置为其对应的顶点,例如经过区域1时将D点视做单一威胁点，经过区域3时将B点视做单一威胁点以此类推。此时无人机受单一引力源与单一斥力源共同作用，与传统APF算法中的情况相同，当无人机飞行至此区域时可以使用传统算法进行下一步路径点的求解。当无人机经过边对应区域时，我们将算法中的威胁点设置为此时无人机位置到威胁区域对应边界垂线的垂足点，该点在该时刻对无人机的斥力方向垂直于该点所在边向外，且无人机距离威胁区域边越近该斥力越大，当无人机无限靠近边缘时，斥力达到无穷大，保证无人机不会进入威胁区域。与第一种情况相同的是此时的目标点及威胁点同样只有一个，亦可以使用传统APF算法进行计算。

在该算法的执行过程上我们可以认为算法在每次计算下一步的路径点时先进行分类讨论，对自身位置进行判断，进而选取相应规则的坐标点作为障碍物。在每一次的下一步航路计算中均只存在一个威胁点，进而可直接使用传统APF算法进行计算，与传统APF算法不同的是每一步的威胁点虽然数量相同，但却不一定是同一个坐标点。威胁点的总数与算法中设置的计算步长有直接的关系，步长设置越大，计算量越小，精度相应更低；步长设置越小，计算量增加，精度相应更高。

2.4 航迹的优化

在仿真的过程中我们发现在某些输入条件下和一些特殊位置(例如区域交接处)，规划出的航迹会发生角度较大的偏转。为了使规划的航迹符合飞行器的转弯性能，在程序中需加入控制转角的条件，从而限制每个路径点之间的最大角度改变量以符合飞行器性能。尖点通常出现在飞行器进入一个新区域时，振荡更多出现在飞行器沿边界飞行时。

改进程序主要是在每次循环计算下一个路径点的方向时，利用判断语句判断前后两次方向角度的差值是否大于设定值，如不大于则保持该值不变，若大于则令其等于最大值。如图8所示，例如令最大转角α=30°，不加限制时转角为θ，可以将下次的路径规划点进行修正[22]。

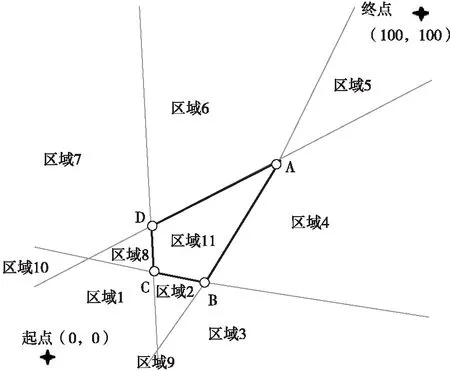
图6 平面区域的划分Fig.6 The division of plane areas

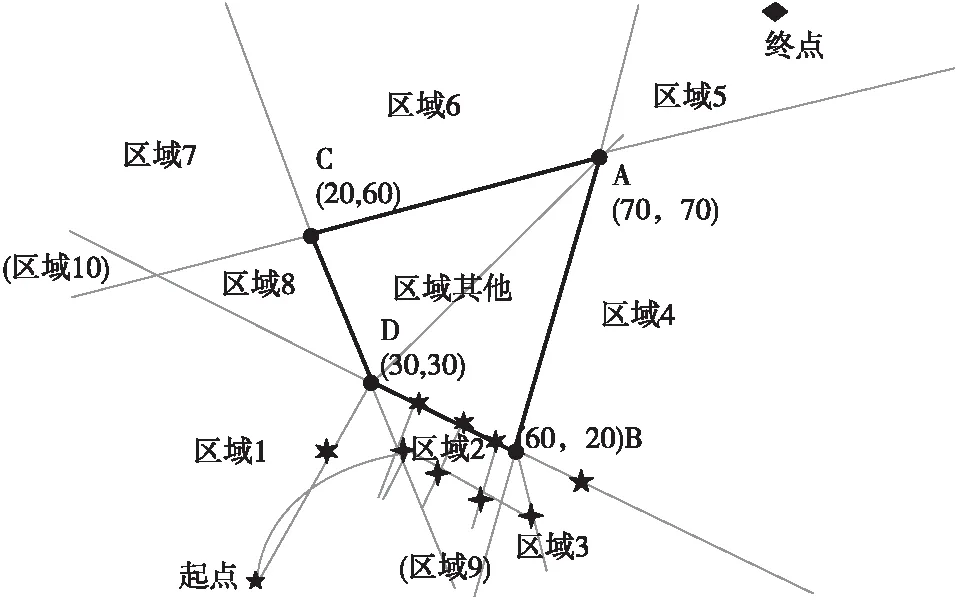
图7 障碍点的选取Fig.7 The selection of obstacle points

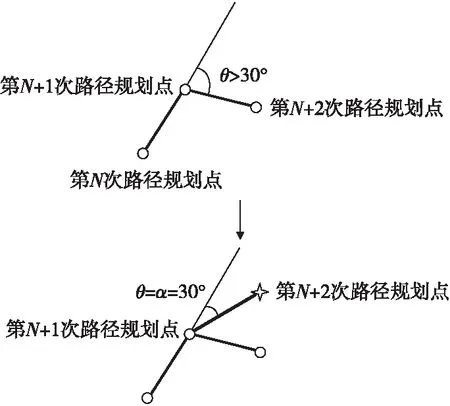
图8 最大转角限制Fig.8 Maximum angle limit

改进的算法流程图如图9所示。

3 仿真验证与结果分析

依据上述建模思路以及现有的传统APF仿真程序在Matlab中设计出改进APF算法。算法主要包含引力计算函数、斥力计算函数、角度计算函数以及算法主体部分共四个文件。

引力计算函数、斥力计算函数可以直接延用传统APF算法中的函数；角度计算函数中加入了航迹角度最大值的限制；主程序中加入了输入边界值的预处理部分、平面划分部分以及多重判断与循环，使无人机明确自身位置进而执行下一步路径点的计算。

对所编写的程序进行多种情况下的输入测试得到多组航迹规划的结果，重点对影响航迹较大的初始变量进行讨论，以及对优化算法的优化效果进行分析。

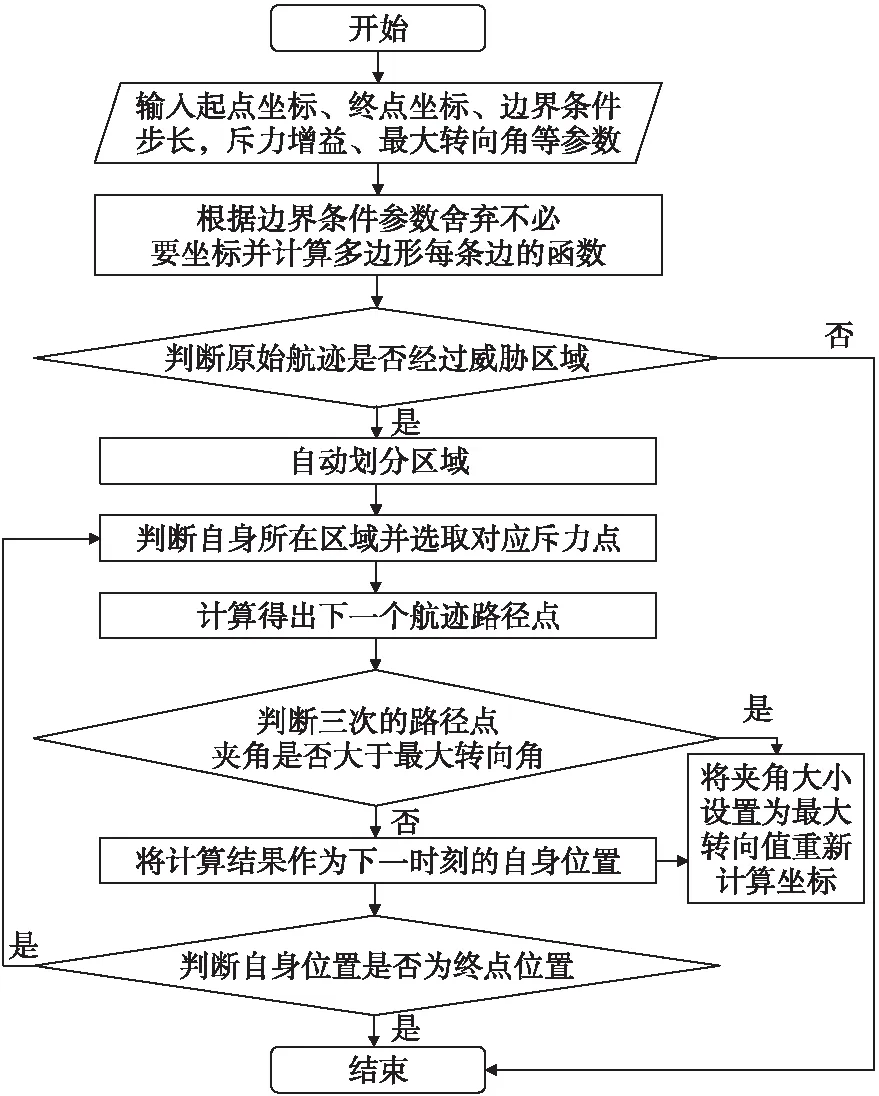
图9 改进算法流程图Fig.9 Flow chart of improved algorithm

以下仿真内容在各幅图像分辨率均设定为 100×100 像素时进行。通过控制区域图像的像素密度与算法计算步长控制总计算量。

首先改变增益系数以及距离影响参数这两个对航迹形状影响较大的参数并对比结果，如图10所示。

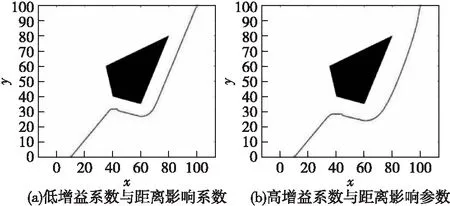
图10 不同斥力增益系数、距离影响参数下的仿真航迹对比Fig.10 Simulation route under different repulsive gain coefficients and distance influence parameters

从仿真结果可见，增大斥力增益系数与障碍影响范围可以使规划出的航迹更加远离威胁区域。斥力的增益系数直接影响了障碍点产生的斥力大小，增大斥力增益系数使无人机受到的合力方向偏离目标点；增大障碍影响距离使无人机更早地受到斥力作用，更早进行偏转规避动作。经过验证，该算法可以通过调节上述两项参数进而根据需求对新航迹路线进行适应性调整。

我们对引入的航迹路径点的最大转角优化部分进行对比分析其效果，如图11所示，左右两图分别为未加入路径点优化与加入了优化程序的航迹结果对比。

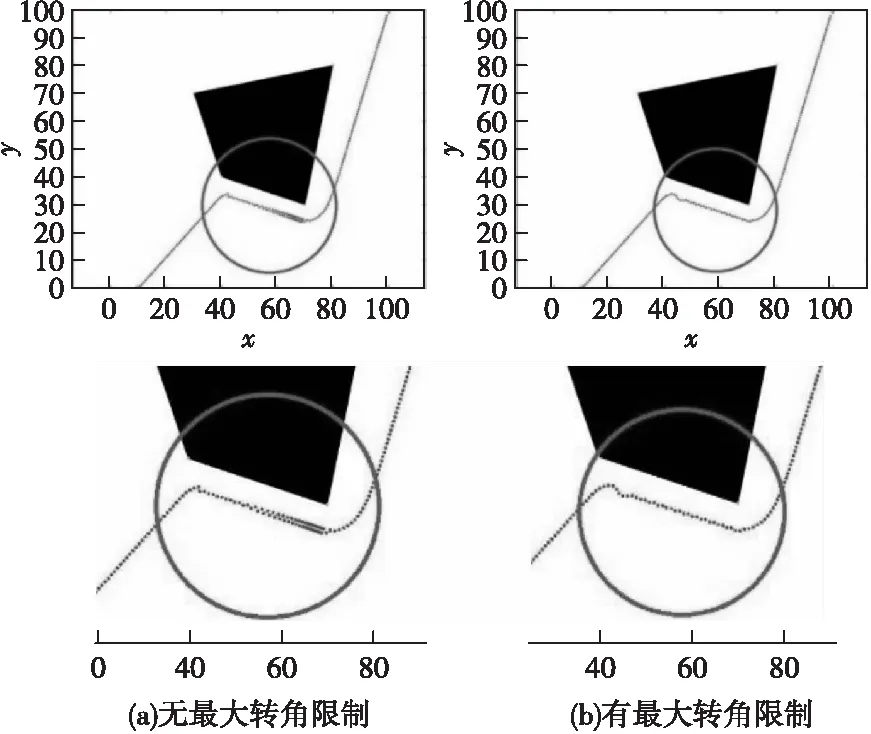
图11 有无最大转角限制的仿真航迹对比Fig.11 Simulation route with and without maximum angle limitation

从仿真结果可见，在未添加角度限制条件时，无人机接近威胁区域时可能会产生尖点，同时在无人机沿威胁区域边界飞行时可能会发生振荡问题。添加角度限制条件可以有效改善航迹规划生成路径中的尖点和振荡点，使路径更为平滑。

最后我们对改进算法与传统算法进行对比，由于传统APF算法并不能针对区域威胁进行计算，这里简单地将威胁区域的重心视为单一威胁点输入给传统APF算法进行计算，如图12(b)。

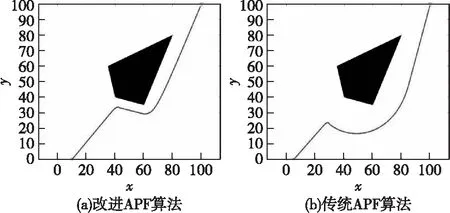
图12 改进APF算法与传统APF算法对比Fig.12 Comparison of the improved APF algorithm with the traditional APF algorithm

通过对比发现，传统人工势场法所规划的路径距离威胁区域的边界过远，无法有效地利用威胁区域周边的安全区域。改进人工势场算法能够更有效地利用特殊威胁区域以外的空间，能使无人机在不穿越威胁区域的前提下更加贴近威胁区域边界飞行。

同时通过对比Matlab程序中的迭代次数，即路径点个数n可对比出使用两种方法得到的航迹的总长度与总计算量上的区别。在将步长设定为0.5时，使用改进APF算法的迭代次数n为382，使用传统APF算法的迭代次数n为507。因此可以得出结论，改进的APF算法相比传统算法，在保证无人机避开威胁的前提下，实现了更低的路径计算量、更短的规划航线以及更短的航行时间。可见改进算法相对传统算法规划出的路径具有更高的效率，实现了“最优航迹规划”原则。