储分一体仓中多穿车复合作业顺序优化问题研究*
2022-08-30王玉聪何杰明廖云飞
王玉聪,何杰明,廖云飞
(1.天津大学管理与经济学部,天津 300072;2.广东烟草惠州市有限责任公司,广东 惠州 516003;3.中国烟草总公司广东省公司,广东 广州 510620)
近年来,随着经济社会的发展和互联网的普及,网上购物已经进入寻常百姓家,这给中国的物流仓储业提出了更高的要求。传统人工作业耗时又耗力,已无法满足当前物流中心的运作需求,自动化的智能仓库应运而生。基于多穿车运行的储分一体仓是新型智能仓的一种,利用多穿车代替人工完成存取货工作,极大地提高了仓储运作系统的效率和准确率。多穿车的调度是储分一体仓的运行关键,由于订单和货物较为零散,又涉及多穿车和提升机的相互作用,如何优化调度使得系统的效率最高,成为企业和学者关注的问题。
1 问题及模型
1.1 问题描述
本文研究了一个储分一体仓的多穿车存取货任务顺序优化问题。已知某物流配送中心的储分一体仓货架有m层n列(共m×n个货位),货位的长度为l、高度为h,每个货位可存放一个托盘。货架的每一层均配有一台多穿车,所有多穿车完全相同,多穿车只需完成本层的出入库任务。货架的前后两端分别设有出入库平台(在货架的底层)和出入库提升机轨道,多穿车与提升机在每层的交接区进行货物交接,提升机负责货物在竖直方向的运输。出入库提升机与多穿车的移动速率分别为vx、vy和vz,所有设备每次均只能搬运一个托盘。现有一批待入库和待出库的任务单,已知任务与货位一一对应。该问题的目标是,合理规划出入库任务的调度顺序,综合考虑任务和设备的等待时间和多穿车的移动距离,使得储分一体系统整体作业效率最高。
1.2 模型假设
不考虑货架上的实际存货情况,即默认入库任务对应的货位为空货位,出库任务对应的货位存有货物。出入库提升机和多穿车均为匀速移动,移动速率为已知常数。不考虑出入库提升机和多穿车的启动和制动过程,忽略装卸货时间。不考虑托盘(货物)的实际大小,货位间距即为出入库和多穿车的移动距离。任务开始前,多穿车的初始位置在货架入库提升机一侧,所有任务完成后,多穿车须返回初始位置。
1.3 模型建立
1.3.1 符号
符号代表的含义如表1所示。

表1 符号所表示的含义

表1(续)
1.3.2 模型
1.3.2.1 目标1:等待时间最短
整个系统的等待时间可分为2部分:①任务的等待时间,即货物到达交接区后,为等待交接所停留的时间;②设备的等待时间,即设备完成上一任务至接收到下一任务间的空闲时间。式(1)表示了等待时间最短这一目标,式(2)—式(4)分别给出了出入库提升机和多穿车的等待时间的计算方法。

1.3.2.2 目标2:移动距离最短
经简单分析,发现出入库提升机的移动均为往返运动,任务确定后则移动确定,故移动距离的优化只涉及多穿车。式(5)表示了多穿车移动距离最短这一目标,须根据任务的先后顺序,分别对移动距离进行讨论。

该模型同时考虑货物和设备的等待时间以及设备的移动距离,为双目标规划问题。为方便求解,利用复合函数将双目标问题转化为单目标问题,这里取2个目标的线性组合作为最终考虑的目标。
1.3.2.3 数学模型
数学模型具体如下。

式(16)—式(31)中:式(6)为目标函数,表示最小化等待时间和设备移动距离;式(7)—式(9)描绘了某一任务的开始时刻;式(10)—式(14)描绘了某一任务到达交接区的时刻;式(15)—式(18)描绘了某一任务在交接区的等待时间;式(19)—式(20)描绘了某一任务的完成时刻;式(21)—式(23)表示每个任务只能由一台出入库提升机和多穿车完成一次;式(24)—式(28)确保出入库提升机和每层多穿车的任务范围,即出库提升机只完成出库任务,入库提升机只完成入库任务,每层的多穿车只完成本层的任务;式(29)—式(31)为决策变量的取值范围。
1.3.2.4 线性化
由于该模型存在非线性的目标函数和约束条件,无法使用求解器直接求解,因此需要线性化。模型中的非线性表达式分为2种,max函数和0-1变量与连续变量相乘,分别出现于目标函数公式(2)—公式(4)和约束条件公式(15)(16)(18)中,通过引入辅助变量μ、u和δ对其进行线性化操作。
对于max函数部分,由于非线性部分的结构相似,为方便表示,表示如下:

根据max函数的线性化方法,式(33)可等价转化为线性约束组,即式(35)—式(40),具体如下:

同理,式(34)也可等价转化为一组线性约束。
对于0-1变量与连续变量相乘的部分,以式(2)为例,式(2)所表达的含义等价于以下公式,即:

根据相关线性化方法,式(41)可等价转化为线性约束组,即式(42)—式(45)。

同理,式(3)和式(4)也可分别转化为一组线性约束。
2 算法设计
本文研究的多穿车存取货路径规划问题较为复杂,不论是目标函数还是约束条件中均包含非线性的部分,即使采用一些转化方法将其线性化,使得求解器可直接对模型进行求解,但随着问题规模的增加,求解难度增加,求解器难以在有限时间内得出最优解。遗传算法是一种仿照生物遗传进化而提出的基于种群的启发式算法,被广泛应用于生车间调度、组合优化、路径优化等问题中,为了提高求解效率,本文采用遗传算法对大规模问题进行求解。
本文所使用的考虑模拟退火的遗传算法基本流程如图1所示。

图1 考虑模拟退火的遗传算法流程图
2.1 编码
本文采用顺序编码方式,为每个出入库任务编号,每个任务即为一个基因,一个个体即为一个出入库方案,其编码顺序即为一个可实施的任务完成顺序。例如某次任务共包含10个出入库任务,分别编号为1—10,则个体[7 8 5 3 10 1 9 2 4 6]表示以7—8—5—3—10—1—9—2—4—6的顺序依次完成相应任务。
2.2 初始种群
本文采用随机生成的方式,根据预设的种群规模,随机生成相应数量的个体组成初始种群。
2.3 适应度函数
基于模型的目标函数,规定对于任意个体i的适应度函数为:

可以看出,某个方案完成出入库任务时的效率越低(等待时间长、多穿车移动距离长),则目标函数越大,该个体的适应度越小,能够遗传给下一代的概率越小。
2.4 选择算子
选择算子用于从种群中选出进行交叉和变异的父代个体,这里采用轮盘赌的方法,根据种群中个体的适应度,按一定的概率随机选取,适应度越高的个体被选中作为父代的概率越大。
2.5 交叉算子
交叉算子仿照的是遗传学中基因重组,即将选中的2个父代个体的基因按一定规则交叉重组后,遗传给子代。本文采用了几种经典交叉算子,包括部分匹配交叉、循环交叉、次序交叉、基于位置交叉和替换交叉算子。
2.6 变异算子
变异算子仿照的是遗传学中的基因突变,即按照一定规则改变某个体的一个或几个基因。本文采用的变异算子包括替换变异、交换变异、简单倒位变异、倒位变异和争夺变异。
2.7 模拟退火接收准则
在整个遗传算法的迭代过程中,考虑模拟退火的接受原则。当经过交叉和变异产生的子代个体适应度小于种群中适应度最小的个体时,则按照的概率接受子代个体加入种群,并将原种群中适应度最小的个体移出,其中Ef为子代个体的适应度的倒数(即对应方案的效率);Eworst为当前种群中最小的适应度的倒数;T为温度,T0=0.85×Eworst0,温度以λ(0<λ<1)的速率下降。
3 实验结果
为验证算法和模型的有效性,本文随机生成了一些算例,通过JAVA调用求解器和编写遗传算法,对问题进行求解。调用的求解器为IBMILOG CPLEX 12.8,运行环境为Intel(R)Core(TM)i5-6200U CPU@2.30 GHz 2.40 GHz处理器和4 GB内存计算机。
3.1 算例及参数
根据实际情况,设货架共包含12层,每层16组通道,每组5个,通道宽0.5 m,由于一组通道放置一种卷烟,这里将一组通道看作一个长2.5 m的货位,层高为0.3 m。出入库提升机的移动速率为1 m/s,多穿车的移动速率为2 m/s。
随机生成一批出入库混合任务及其对应货位的坐标。除随机摆放的算例外,根据货物在竖直方向集中摆放位置,即上(H)、中(M)和下(L),将算例分为3类;根据货物在水平方向集中摆放的位置,即左(L_)、中(M_)和右(R_),将算例分为另外3类,每个算例包含100个任务。其他各参数设置如表2所示。

表2 参数表
3.2 实验结果
对于每种算例,将遗传算法运行5次,取其中的最优解,表3为遗传算法求解各类算例的平均结果。可见,遗传算法的求解效率远高于求解器。

表3 遗传算法求解各类算例的平均结果
图2为不同货物摆放情况的算例的求解结果对比。从图2中可以看出,货物摆放对多穿车的移动距离影响不大,L_类算例,即货物集中摆放于货架左侧时,多穿车的移动距离较其他算例略少。L_、M_、R_类算例的等待时间普遍长于H、M、L类算例,说明货物在竖直方向摆放越分散,可能导致等待时间越长;而L_、M_、R_类算例等待时间依次递增,说明货物集中在货架左侧时的等待时间较短,集中在货架右侧时的等待时间较长。整体上来看,L类算例的求解结果较好,因此若货位多于货物量,应优先放置于货架下部,能够获得最高的运作效率。
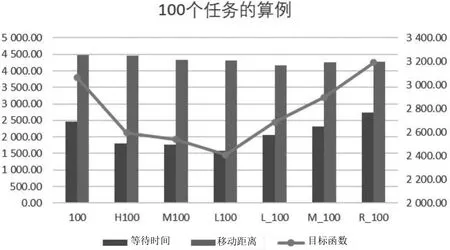
图2 不同货物摆放情况的算例的求解结果对比
4 结论
本文研究了储分一体仓中单层多穿车的复合作业优化问题,用出入库任务和设备的共同等待时间和多穿车的移动距离来衡量系统的效率,旨在通过优化,找出使系统效率最高的作业顺序。基于多穿车的作业流程,建立了相应的数学优化模型,通过随机生成的算例对模型进行求解。由于模型较为复杂,本文使用了一种考虑模拟退火的遗传算法对问题进行求解。
通过设置货物不同的摆放位置,生成7类不同的算例,对比实验结果发现,货物摆放对多穿车的移动距离影响不大,但货物在竖直方向摆放越分散(即占用的层数越多),总的等待时间会越长,总体来看,货物集中于货架左下侧时系统的效率最高。
