基于改进经验模态分解的汽车后视镜电机故障诊断方法

吴 骏，陆晔敏，王玉峰

（麦格纳（太仓）汽车科技有限公司，江苏 苏州 215000）

随着汽车技术的发展，汽车后视镜从传统的拉索式结构后视镜转变为由电机驱动控制，具备可自动调节位置、驻车收缩折叠和角度记忆等功能。后视镜电机是汽车电动后视镜的核心组成部分，其工作状态直接影响到电动后视镜的安全运转。国内的电动后视镜生产厂家缺乏完善的故障诊断系统，则导致不合格的汽车电动后视镜流入市场，进而导致车辆意外事故的发生。目前在生产过程中使用的故障诊断方法是人工听检方法，但其存在标准不统一、检测效率低、劳动强度大、损害听力健康等局限性。振动信号作为汽车后视镜工作发出的固有信号，能够反映后视镜运行状态，为故障诊断提供了合理的依据。

电动后视镜的振动信号是一种非线性、非平稳信号，在分析此类信号时，以快速傅里叶变换为基础的分析方法已不能满足要求。目前常用的信号时频分析方法有GABOR提出的短时傅里叶变换（STFT）、Wigner-Ville分布（WVD）和小波变换（WT）等[1]。上述的时频分析方法在一定程度上解决了非线性、非稳态信号分析的困难，但是都不能避开时间分辨率与频率分辨率冲突的矛盾。HUANG于1998年提出Hilbert-Huang变换[2]，其中该方法提出了以本征模态函数为基本时频信号，不依赖于传统信号分析理论的束缚。它通过定义信号的瞬时频率，能够精确表达信号频率变化，适合分析非平稳信号[3]。

本文提出一种方法，先将振动信号进行经验模态分解（Empirical Mode Decomposition，EMD），使用希尔伯特变换（Hilbert Transformation，HT）将每一个本征模态函数进行解调制，得到信号的瞬时频率、瞬时幅值，根据所得的数据绘制希尔伯特谱，该希尔伯特谱包含了信号的时频信息。对瞬时频率与瞬时幅值取若干特征，引入BP神经网络，对后视镜电机故障模式分类器进行训练，建立HHT-BP的分析模型。实验结果表明，可以通过HHT-BP的方法判断出汽车后视镜电机存在的冲击故障。

1 HHT的基本原理

希尔伯特-黄变换（Hilbert-Huang Transformation，HHT）的振动信号特征提取方法分为经验模态分解、希尔伯特变换、本征函数特征提取3个步骤。

任何复杂的信号都是由一些相互独立的固有模态函数（Intrinsic Mode Function，IMF）所构成，每一个IMF分量可以是线性的也可以是非线性的，对于一段数字信号x（t），经过经验模态分解后可表示为以下等式[4]：

式（1）中：ci为第i阶IMF分量；rn为余项函数。

对每个IMFci作Hilbert变换，算法如下：

构造解析信号为：

式（3）中：ai（t）为解析信号的瞬时幅值函数；为解析信号的瞬时相位函数。

2 实验设备与特征提取

本文所选用的测试样品为麦格纳汽车科技有限公司所提供的电动后视镜产品，其额定工作电压为12 V。在数据采集过程中，设置的采样频率为100 kHz，所使用的测振设备为压电式振动传感器。样品电机与传感器测点位置如图1所示。

图1 故障电机振动信号的经验模态分解

将采集完的振动信号进行EMD分解，选取的最大分解阶数为10阶，图2、图3分别为故障电机与健康电机各自的10阶IMF曲线与余项函数随采样点的变化情况。

图2 故障电机振动信号的经验模态分解

图3 健康电机振动信号的经验模态分解

第1节所述方法提取了样本信号的10阶IMF分量曲线与余项函数曲线。但由于在提取IMF分量时使用了3次样条拟合的方法，引入了端点处的震荡，需要对IMF分量进行筛选，去除与原样本信号相关度较小的IMF分量[5]，保留与原信号相关度较大的分量。

本文定义了原始信号与IMF间的相关度函数与阈值T，相关函数的公式为：

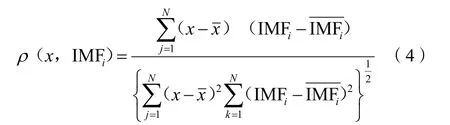
阈值选取如下公式，即：

式（5）中：通常情况下η的取值为10[6]。

故障电机和健康电机各阶IMF曲线与原信号的相关度分别如表1、表2所示。

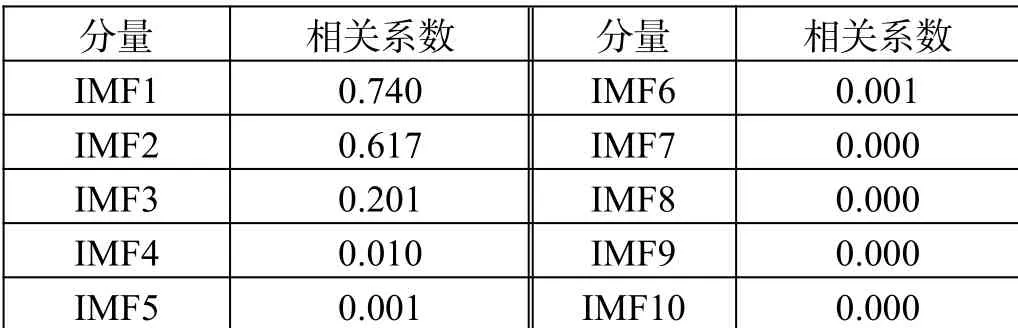
表1 故障电机各阶IMF曲线与原信号的相关度

表2 健康电机各阶IMF曲线与原信号的相关度

根据公式（5），故障电机的相关系数筛选阈值为0.07，相关系数低于0.07的IMF分量被筛去；同样，健康电机的相关系数筛选阈值为0.09，相关系数低于0.09的IMF分量为虚假的IMF分量，不能体现原始信号的特点，故在分析IMF分量特征时，应当根据公式（5）舍弃相关系数低于筛选阈值的IMF函数。对筛选后留存的IMF分量，本文提取出以下4个特征[7]：平均瞬时频率、各层IMF的平均能量各、各层的平均总能量 层IMF能量占比

故障电机和健康电机各阶IMF曲线特征提取如表3、表4所示。

表3 故障电机各阶IMF曲线特征提取

表4 健康电机各阶IMF曲线特征提取

通过对比故障电机与健康电机所提取的特征，可以得到故障电机振动总能量较小，第二阶IMF分量能量占比远远比健康电机多，而健康电机振动信号的能量集中在第一阶IMF里。图4—图7分别为故障电机与健康电机的希尔伯特谱，从图中可以看到故障电机信号在2 200 Hz处存在冲击，合理地解释了故障电机信号在第二阶IMF分量中占比高于健康电机的现象。

图4 故障电机振动信号的希尔伯特谱

图5 故障电机振动信号的希尔伯特时频谱

图6 健康电机振动信号的希尔伯特谱

图7 健康电机振动信号的希尔伯特时频谱

相比于故障电机，健康电机的希尔伯特谱则反映出以下特点：①能量分布均匀，集中体现在5 000 Hz左右；②总能量较大，第一阶IMF占能量比非常大；③振动冲击成分较少。

由于希尔伯特谱只能定性地描绘电机的工作状态特征，无法进行定量的进行分类，故本文引入了BP神经网络，对经过EMD分解与IMF分量筛选后的信号根据所选特征进行分类。将所选特征融合为一个十维的特征向量其中为前三阶IMF分量平均瞬时频率；为前三阶IMF分量平均能量；Eall为IMF分量的总能量；r=[r1r2r3]，为前三阶IMF分量平均能量占总能量比例。以特征向量p作为BP神经网络的输入，建立信号分类模型。

3 BP神经网络进行电机状态的分类

BP神经网络进行分类的过程分为2个阶段：第一阶段将输入信息从输入层经过隐藏层逐层计算输出；第二阶段通过输出误差逐渐向前计算各个隐藏层的误差，根据此误差修正前一层的权重值[8]。BP神经网络具有高度自学习和自适应的能力，可以很好地适应后视镜电机的振动信号分类[9]。建立BP神经网络，其中隐藏层层数为12，输出维度为2，如图8所示。

图8 BP神经网络分类模型

该BP神经网络的数学描述如下：

式（6）—式（9）中：ωij为隐藏层第i个节点到第j个节点的权值；xi为输入层第i个节点的输入；θi为隐藏层第i个节点的阈值；φ为隐藏层的激励函数；ak为输出层k个节点的阈值[9]；φ为输出层的激励函数。

本文一共选取了73个样本信号，包含49段正常电机振动信号、24段故障电机信号，每段信号长度1 s。图9为BP神经网络分类的混淆矩阵，在训练过程中，达到了91.5%的识别率，其中有2个故障样本被误判为健康样本，有3个健康样本被误判为故障样本。在验证与测试的过程中均达到了85.7%的识别率，整体的BP神经网络识别率达到了90.4%，基本完成了分类的任务。

图9 BP神经网络分类混淆矩阵

表5为BP神经网络在测试集中输出的结果。其中将一个故障样本误判为正常的结果，出现该结果的原因可能是该神经网络的训练集合样本数量较少，泛化能力还有提升的空间。但是从结果上分析，该HHT-BP模型已经满足了故障诊断的准确率要求。

表5 BP神经网络测试集结果

4 结论

本文所提出的HHT-BP分析模型在处理后视镜电机振动信号中有良好的成效。通过经验模态分解与希尔伯特变换得到振动信号的希尔伯特谱，再根据希尔伯特谱中的信息，提取平均瞬时频率、平均瞬时能量、总能量、能量占比等10个特征指标。将每一段振动信号提取指标后，将其作为特征向量输入本文所建立的BP神经网络分类模型中进行识别。实验结果表明，该BP神经网络具有较高的准确识别率，能够较好地应用于现实检测环境中。