基于重频随机捷变的切片组合干扰抑制方法研究

谢登召，蒋路华，沈佳琪

(中国船舶集团有限公司第八研究院，江苏 扬州 225101)

0 引 言

随着信息技术的不断发展，传统的海战已发展成为海、空、网、电等跨域协同的多维立体战。反舰导弹作为信息化海战中的重要武器装备，是水面舰艇面临的主要威胁之一，其发展一直受到世界各国的关注。为了有效应对反舰导弹的威胁，世界各国的水面舰艇均装备有舰载电子对抗系统，其中以美军的AN/SLQ-32电子对抗系统为主要代表。而目前正在研制中的AN/SLQ-32(7)电子对抗系统，采用了先进的有源电扫阵列(AESA)技术，大幅度提升了对反舰导弹的干扰能力，这给反舰导弹突防作战的有效实施带来了巨大挑战。

目前，电子对抗系统主要采用切片组合干扰，通过将采样的雷达信号调制后放大再转发给雷达进行干扰。这种干扰样式兼具压制性和欺骗性的特点，能够对雷达的目标检测造成巨大威胁。而对于切片干扰的抑制，王存卫等人提出基于发射验证信号来剔除干扰的方法，不过该方法不能适应快速响应的干扰机。韩博文等人提出结合分数阶傅里叶变换(FrFT)与分数阶域滤波的抗切片组合干扰方法，但该方法会带来干扰抑制后目标主瓣展宽等问题。王晓戈等人提出基于时域滤波信号重组的抗切片组合干扰方法，该方法能降低距离旁瓣对雷达目标检测的影响，但抑制过程中会损失目标能量。张亮等人提出基于快慢时间域处理估计干扰参数来重构干扰信号，通过对消实现干扰抑制，但估计干扰信号可能会引入新的干扰。

针对上述问题，本文提出一种基于重频随机捷变的切片组合干扰抑制方法，首先对切片组合干扰的产生原理进行建模，然后对基于重频随机捷变的切片组合干扰抑制方法进行理论分析，最后进行数值仿真。本文的研究结果对提高反舰导弹末制导雷达抗干扰能力具有一定的参考意义。

1 切片组合干扰的数学模型

切片组合干扰的信号产生过程如图1所示，首先用等间隔的矩形脉冲串对雷达信号()进行采样，得到干扰样本信号()，此为斩波阶段；然后通过若干次的复制填充处理，使干扰样本信号全完填充满右侧相邻的空时隙，并生成干扰信号()，此为交织阶段。

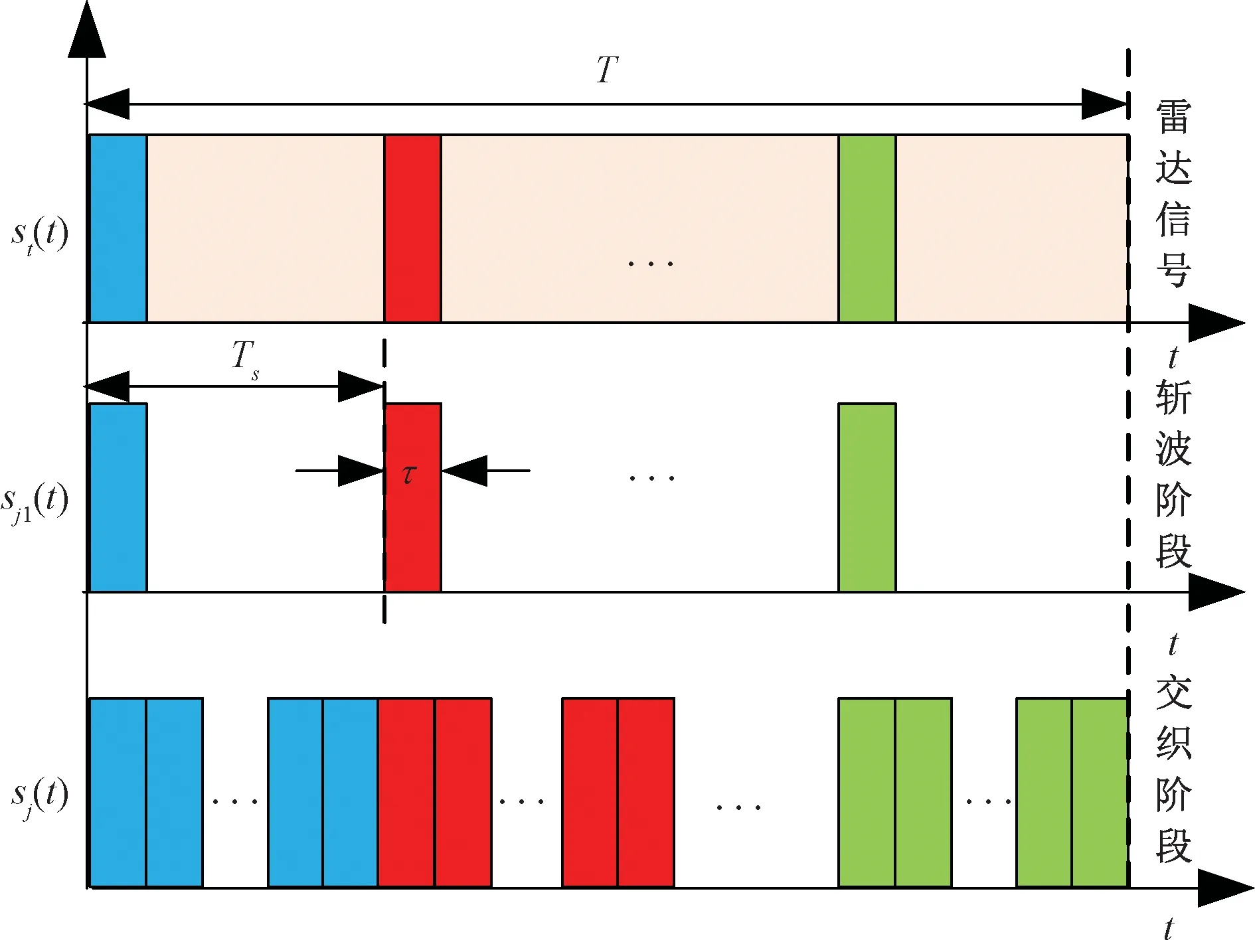
图1 切片组合干扰的信号产生示意图

假设雷达发射信号为线性调频(LFM)脉冲信号，信号表达式为：

(1)

式中:为脉冲宽度；=为调频斜率；为信号的带宽；为信号载波频率。

设干扰的采样脉冲串为:

(2)

式中:为采样脉冲宽度；为采样周期；⊗为卷积符号；(·)为冲激函数。

于是可以得到采样后的信号为：

()=()()

(3)

通过复制，可以得到切片组合干扰的表达式为:

(4)

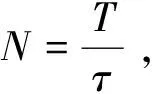
图2为通过切片组合干扰产生的干扰信号时域波形，这个干扰信号通过雷达脉冲压缩处理后，其结果如图3所示。

图2 干扰信号的时域波形

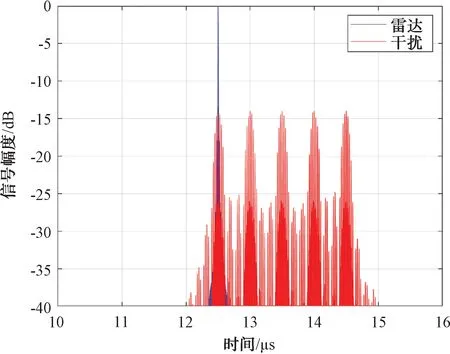
图3 干扰信号经过脉冲压缩后的输出

由图3可以看出，经过雷达脉冲压缩处理后，在目标后产生大量密集的假目标群，这将给雷达的目标探测和跟踪带来巨大的挑战。为此，需要采取具有针对性的抗干扰措施。

2 基于重频随机捷变的干扰抑制算法

尽管目前的雷达对抗设备已具备精确复制雷达脉内信息产生相干干扰的能力，但当前的干扰技术产生器必须通过重频跟踪器来跟踪和预测雷达下一时刻的发射信号。因此，可以通过重频随机捷变来破坏其对雷达的跟踪和预测，进而抑制干扰。假设雷达共发射了个脉冲，脉内调制为线性调频，载频为，对应的慢时间为，则重频随机捷变雷达信号模型可以表示为:

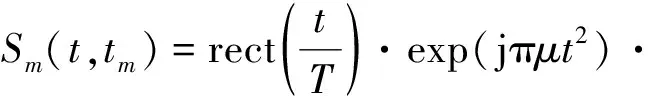
exp(j2π(+))

(5)

式中：为慢时间；=(-1)+()Δ,为平均脉冲重复周期，Δ为最小重频捷变间隔，()∈{1,2,…,}，表示重频捷变序列；=，为调频斜率，为信号带宽，为脉冲宽度。

基于重频随机捷变的干扰抑制算法流程图如图4所示。具体为当识别到干扰存在时，立即改变雷达的脉冲重复周期(PRT)，而干扰机由于不能实时跟上雷达PRT的变化，这样干扰信号和目标回波信号的相对延时会发生改变，雷达接收机可以根据发射信号的PRT将回波信号进行包络对齐，然后再通过脉冲积累、门限处理等手段抑制切片组合干扰。

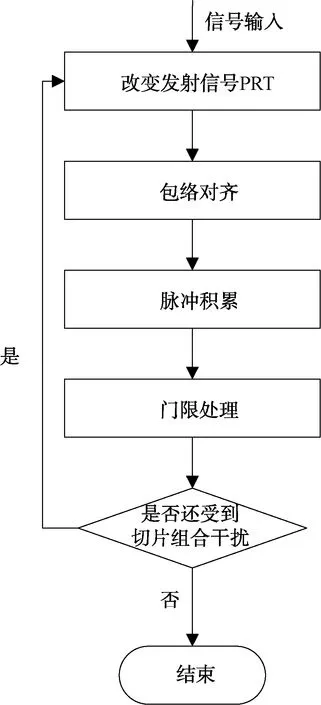
图4 干扰抑制算法流程

3 数值仿真

根据上述理论模型进行数值仿真，仿真中所选取的参数如下：带宽120 MHz，脉宽20 μs，重频的平均值为10 kHz，载频为18 GHz，信号的脉内调制方式为线性调频(LFM)，目标位于50 km处，目标的信噪比为-15 dB，积累脉冲数目为256个，干扰信号为切片组合干扰。图5为雷达脉冲压缩处理前后的结果。

图5 雷达脉冲压缩处理前后的结果

由图5可以看出，在脉冲压缩之前，回波信号存在非常强的噪声和干扰；经过脉冲压缩以后，噪声得到抑制，但目标周围仍存在强干扰，这时若不采取抗干扰措施，则很难实现对目标的跟踪。

图6和图7为经过重频随机捷变进行干扰抑制前后的雷达对目标的跟踪距离和跟踪误差曲线。

图6 跟踪距离

图7 距离跟踪误差

由图6和图7可以看出：当不存在干扰时，雷达能够稳定跟踪50 km处的目标，距离跟踪误差基本可以忽略；当存在切片组合干扰时，雷达的跟踪被破坏，雷达跟上了干扰，此时距离跟踪误差约为340 m，这对于反舰导弹来说打击已失败。当采取抗干扰措施后，干扰没法破坏雷达对目标的跟踪，尽管干扰能够影响雷达对目标的跟踪，但此时跟踪误差仅在10 m左右。这对于舰船这种大型目标来说，跟踪精度可以满足要求，因此可以完成相应的作战任务。

4 结束语

本文针对切片组合干扰的抑制方法开展研究，提出一种基于重频随机捷变的干扰抑制算法。该算法通过改变雷达的PRT来破坏干扰机的跟踪，然后再通过脉冲积累、门限处理等手段抑制干扰。数值仿真结果表明，当采用该算法后，切片组合干扰无法破坏雷达对目标的跟踪，距离跟踪误差从干扰抑制前的340 m降低至将近10 m。本文的研究结果对于提高反舰导弹末制导雷达抗干扰能力具有一定的参考意义。