冲激噪声背景下线性调频信号参数估计
2022-08-30蒋东旭任培林
蒋东旭,任培林
(中国船舶集团有限公司第八研究院,江苏 扬州 225101)
0 引 言
线性调频(LFM)信号以其大时宽带宽积、易工程实现等特点,广泛应用于雷达、声呐等高分辨探测领域。由于其重要性,对其进行参数估计是现代电子侦察的重要任务之一。
文献[2]中陈浩等人提出利用连续小波变换实现高精度LFM信号参数估计方法,但是其存在小波基选取困难和实时性差等问题。文献[3]中黄响等人提出了基于分数阶傅里叶变换(FrFT)的参数估计方法,通过搜索FrFT域参数实现LFM信号参数估计。
然而上述方法均假设背景噪声服从高斯分布,实际工程中经常会出现时域幅度具有冲激特性的噪声,即冲激噪声。对于此类噪声,常用对称α稳态分布(SαS)来描述。文献[5]中李立萍等人提出修正的低阶矩模糊函数结合Radon变换的冲激噪声环境下LFM信号参数估计方法,但是该方法需要二维搜索,运算量很大。文献[6]中金艳等人提出利用压缩变换抑制冲激噪声,并结合具有快速数值计算的FrFT实现冲激噪声环境下LFM参数估计,相比于文献[5]的方法,运算效率有较大提升。本文选择具有良好限幅一一映射特性的双曲正切函数对冲激噪声实现有效抑制,并利用抑制噪声后信号的延时自相关得到高精度LFM参数估计。仿真实验表明,与文献[5]所提方法相比,本文所提方法在低信噪比情形下具有更佳的LFM参数估计性能,且无超参数需要调整。
1 数据模型
假设冲激噪声背景下接收机接收到的LFM信号满足以下模型:
()=exp[j2π(+05)]+()
(1)
式中:、、分别为LFM信号的幅度、起始频率和调频斜率;()为冲激噪声,服从SαS分布,因为SαS分布没有类似高斯分布的统一解析概率密度表达式,通常采用其特征函数表示为:
()=exp(-||)
(2)
式中:为分散系数,表征了噪声幅度的分散程度;为特征指数,且0<≤2,越小,噪声冲激特性越强,当=2时,其退化为高斯分布。
2 算法简述
如图1所示,双曲正切tanh函数与输入是一一映射,具有可逆性,在输入接近于0时具有近似线性特性;当输入远大于0时,输出接近于1,其具有良好的限幅特性。因此,其对于冲激噪声具有良好的抑制特性。
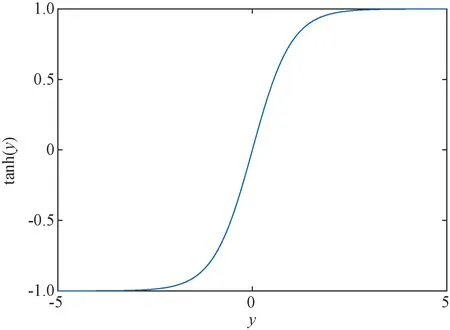
图1 双曲正切函数示意图
对tanh函数进行泰勒级数展开:
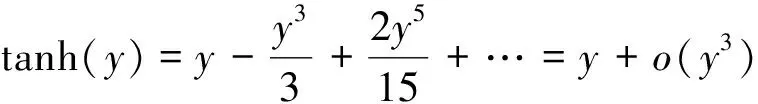
(3)
对式(1)中输入信号()进行双曲正切变换如下:
()=tanh(|()|)·sgn{()}
(4)
式中:sgn表示符号函数,当其输入为复数时,其输出为sgn{}=||。
该变换主要是改变了幅度信息,而相位信息通过符号函数保留了下来。当输入信号无噪声时,()=tanh()exp[j2π(+05)],因此,该变换主要抑制了冲激噪声,而保留了信号。
对变换后的信号()进行延时自相关:
()=(-)()
(5)
式中:上标*表示共轭。
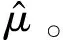

()=()·()
(6)

3 仿真分析

仿真实验一:假设LFM信号幅度为1,起始频率=5 MHz,调频斜率=5 MHz/μs,脉宽2 μs,采样率50 MHz。SαS分布噪声特征参数=12,改变GSNR,使其从-10 dB变化到30 dB,间隔5 dB,在每个GSNR下进行1 000次蒙特卡洛仿真实验,统计起始频率和调频斜率估计的均方根误差(RMSE),仿真结果如图2所示。

图2 LFM信号参数估计性能随广义信噪比变化关系
由图2仿真结果可知,随着GSNR的升高,所提方法和CT-FrFT方法所估计的起始频率和调频斜率均方根误差均降低,表明所提方法有效,同时在≤15 dB时,所提方法参数估计均方根误差均明显小于CT-FrFT方法,这表明所提方法具有更好的中低信噪比下参数估计性能。
仿真实验二:LFM信号参数设置与仿真实验一相同,=5 dB,改变SαS分布噪声特征参数,变化范围为1到2,间隔0.1,在每个下进行1 000次蒙特卡洛仿真实验,相应的参数估计性能如图3所示。
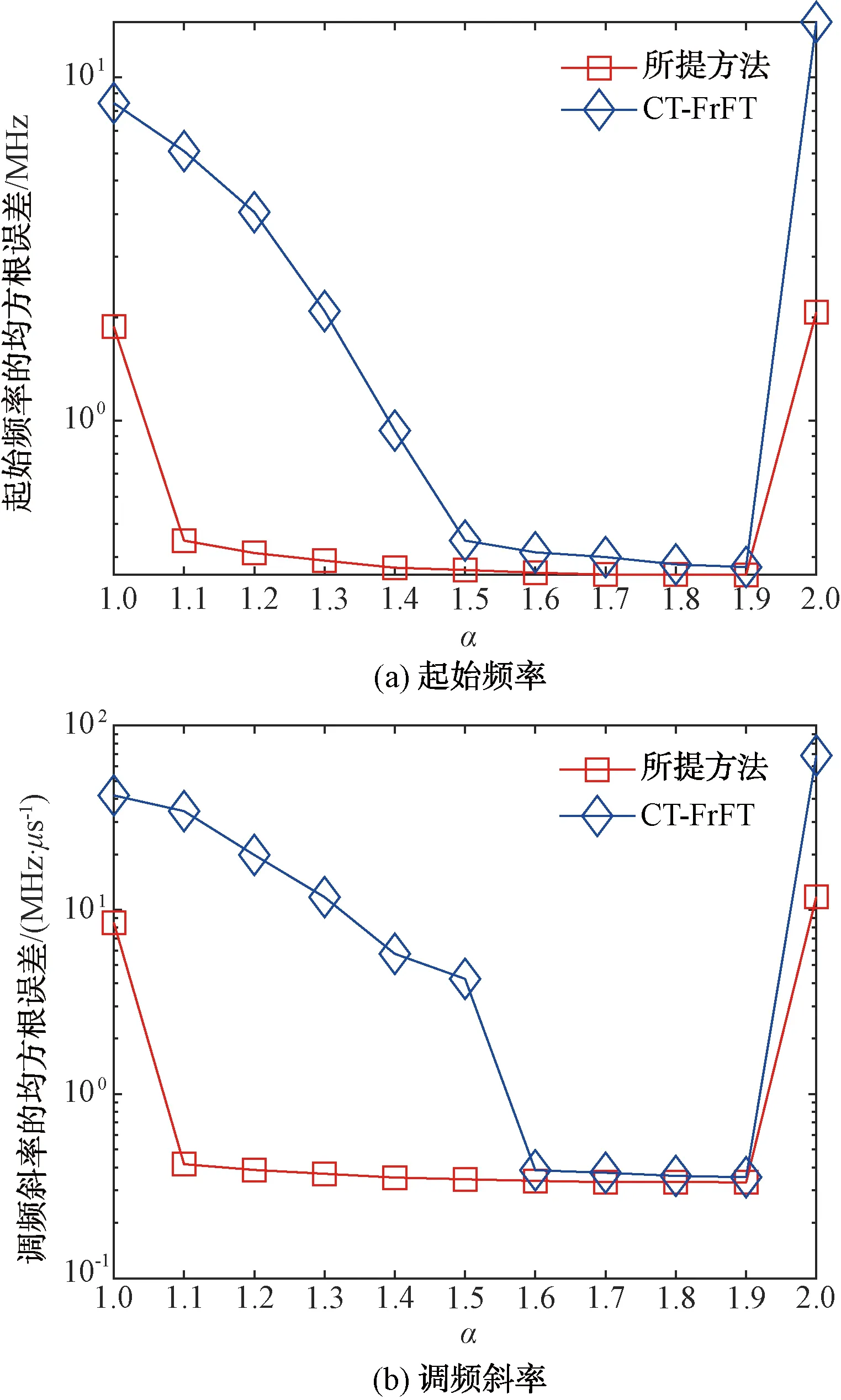
图3 LFM参数估计性能随SαS分布噪声特征参数变化关系
由图3可知,相比于CT-FrFT方法,本文所提方法对于强冲激特性(=1)噪声和高斯噪声(=2)均具有更好的估计性能,且没有额外的超参数需要设置。
4 结束语
本文针对现有冲激噪声背景下LFM信号参数估计方法计算复杂度高、需要设置超参数等问题,选择具有良好限幅特性的双曲正切函数对冲激噪声实现有效抑制,并利用抑制噪声后信号的延时自相关得到高精度LFM参数估计。仿真实验表明,与现有方法相比,本文所提方法在低信噪比情形下具有更佳的LFM参数估计性能,且无超参数需要调整。
