数学向量与三角函数知识在高中物理中的应用例析
2022-08-29甘肃高会平
甘肃 高会平
《普通高中物理课程标准(2017年版2020年修订)》指出,“物理学基于观察与实验,建构物理模型,应用数学等工具,通过科学推理和论证,形成系统的研究方法和理论体系”。在《普通高中数学课程标准(2017年版2020年修订)》中指出,“向量理论具有深刻的数学内涵、丰富的物理背景。向量既是代数研究对象,也是几何研究对象,是沟通几何与代数的桥梁。可用向量语言、方法表述解决现实生活、数学和物理中的问题”。充分体现了数理是一家,也体现了向量在物理中的重要作用。
向量具有“数与形”两方面的特性,其“数”是用一组有序实数对来表示向量的大小和方向;“形”是用一条有向线段来表示向量大小和方向。向量的概念、表示方法和运算法则的确立,使几何图形得以量化,图形之间的关系代数化,对于复杂的图形,只要能把几何图形中的点、线、角等几何元素用向量来表示,并研究这些向量之间的关系或利用这些向量之间的关系研究两个图形之间的关系,再进行向量的运算,就能得到准确的解,再把解转化为几何图形间的关系。
矢量是高中物理中的一个重要的量,贯穿于整个物理学习的始终,无论是在对物体受力分析、运动过程的分析还是在电磁学中都有广泛地使用。而物理中矢量的运算法则和数学中向量运算法则完全一样,除此之外还会用到三角函数与解三角形等知识来进行求解。
一、根据向量加法法则和解三角形知识研究矢量的合成与分解
1.向量加法法则有三角形法则和平行四边形法则。
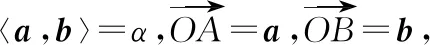
2.在△OAC中,∠OAC=π-α,根据余弦定理,有
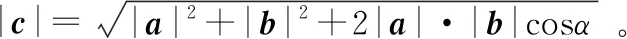
当α=0°时,向量a与b方向相同,所以|c|=|a|+|b|;当α=180°时,向量a与b方向相反,所以|c|=||a|-|b||;当0°<α<180°时,||a|-|b||<|c|<|a|+|b|。
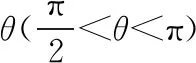
( )
A.一定增大
B.可能不变
C.可能增大,也可能减小
D.当夹角0°<θ<90°时,合力F一定减小
【解法1】矢量图示法

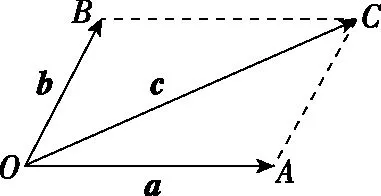
图1

图2
【解法2】解三角形法
如图3,在△OAB中,根据余弦定理
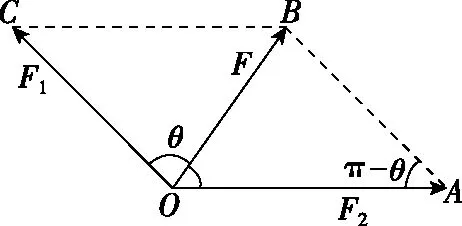
图3
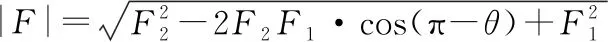
所以,由二次函数的性质可知,合力F的大小在区间(0,-F1·cosθ)内单调递减,在区间(-F1·cosθ,+∞)内单调递增,当F2=-F1·cosθ时,Fmin=F1·sinθ,如图4所示,故选BC。
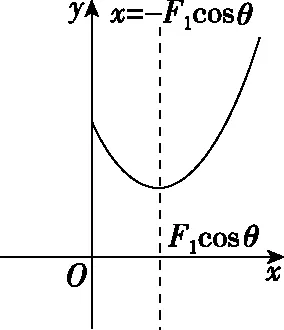
图4
【点评】方法1是利用合力矢量图求解,可以很直观地看出合力F的大小变化规律;方法2利用余弦定理和二次函数的性质,推理计算出合力F的变化规律,有利于培养学生的数学应用意识。
【例2】将一个质量为m的铅球放在倾角为α的斜面上,并用竖直挡板挡住,铅球处于静止状态,如图5所示。缓慢逆时针绕O点转动挡板至水平位置,不考虑铅球所受到的摩擦力,试分析铅球对挡板的压力和对斜面的压力的大小变化。
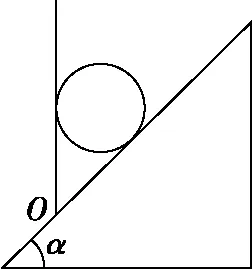
图5
【解法1】设球受到的重力为mg,挡板对小球的压力为N1,斜面对小球的支持力为N2,如图6所示,因三力处于平衡状态,则三力合成的矢量图是封闭的三角形,如图7所示,随着挡板的转动,N1先减小,后增大,当挡板与斜面垂直时,N1取最小,因为N2方向不变,所以N2一直在变小,且当挡板处于水平位置时,N2取值最小为0。而小球对挡板与斜面的压力分别与N1、N2方向相反,但大小变化相同。
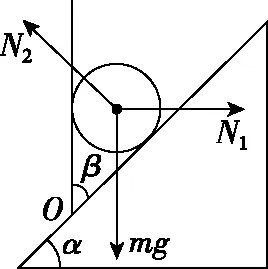
图6
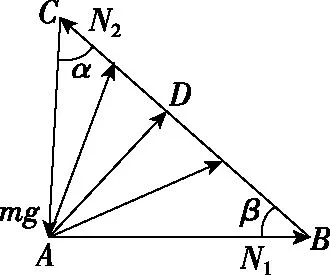
图7

【点评】解法1是矢量图示法,关键是要先确定恒力和方向不变的力,其次利用三角形法则,画出不同状态下的三力平衡矢量图来研究力的变化情况,这就是“化动为静,静中求动”的解题策略;解法2是利用正弦定理、诱导公式、三角函数的性质、极限等数学知识分析力的变化。
二、利用向量的正交分解和直角三角形知识解力的平衡问题。

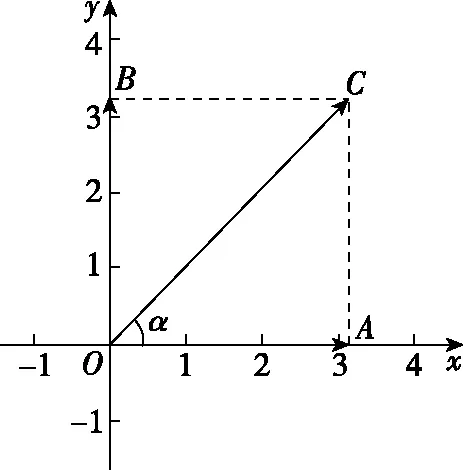
图8
设矢量a和b与x轴的夹角分别为α和β,合矢量记为c,如图9所示,则他们在x轴和y轴方向上的分矢量分别可写成:

图9
ax=a·cosα,ay=a·sinα;
bx=b·cosβ,by=b·sinβ;
cx=ax+bx=a·cosα+b·cosβ;
cy=ay+by=a·sinα+b·sinβ
矢量c的大小为
【例3】(2019·全国卷Ⅲ·3)(改编)用卡车运输质量为m的匀质圆筒状工作,为使工件保持固定,将其置于两光滑斜面之间,如图10所示。两斜面Ⅰ、Ⅱ固定在车上,倾角分别为30°和60°。重力加速度为g。当卡车沿平直公路以加速度a水平向右做匀加速直线运动的过程中,求圆筒对斜面Ⅰ、Ⅱ压力的大小。
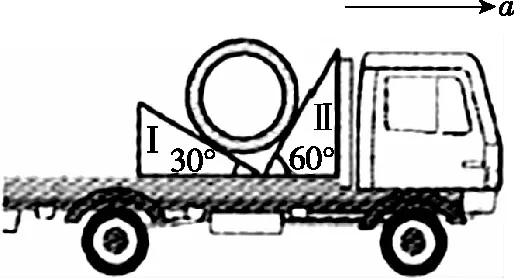
图10
【解析】设两斜面对圆筒的支持力分别为N1、N2,则圆筒对两斜面的压力与N1、N2大小相等,方向相反,设为F1、F2。
解法1:建立以水平和竖直方向为坐标轴的正交坐标系,如图11所示,根据物体的运动状态,可列出水平和竖直方向的运动方程
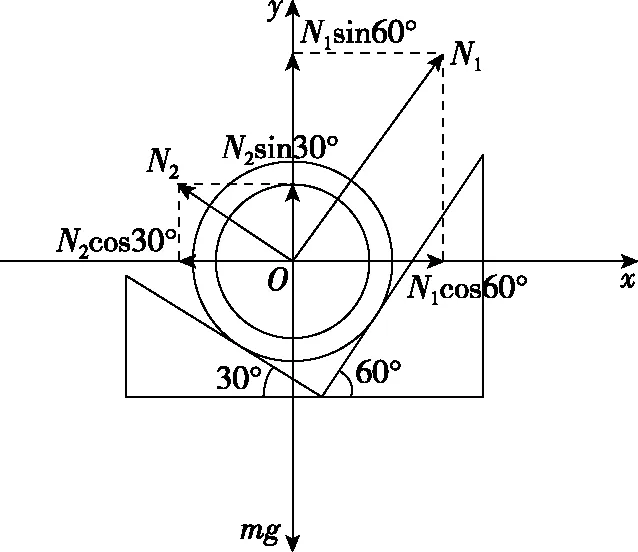
图11
N1cos60°-N2cos30°=ma
①
N1sin60°+N2sin30°=mg
②

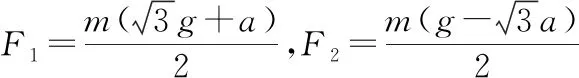
解法2:建立沿两斜面Ⅰ、Ⅱ方向的正交坐标系,且将加速度分解到两坐标轴上,如图12所示。
则有N1-mgcos30°=masin30°,mgsin30°-N2=macos30°;
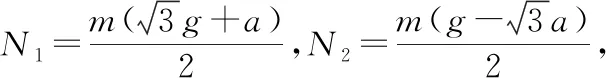
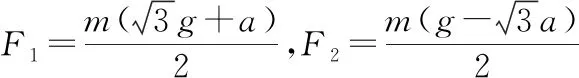
【解法3】在卡车运动过程中,圆筒除了受到竖直向下的重力mg,还受到两斜面对圆筒的支持力N1,N2,由重力mg的起点至支持力N2的终点的矢量就是这三个力的合力ma,如图13所示,则
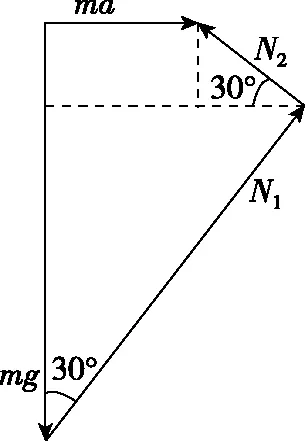
图13
则有N1cos30°+N2sin30°=mg,N1sin30°-N2cos30°=ma
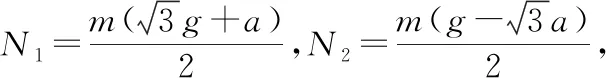
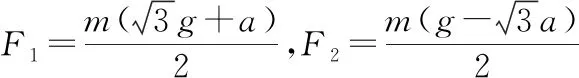
【点评】解法1和解法2都是正交分解法,但建系方法不同,体现了根据问题的特点建立所需的坐标系。对于运动平衡状态,首先对研究对象进行受力分析,画出受力示意图;其次依据平衡条件,建立恰当的直角坐标系;第三,根据图示,寻找几何关系;第四,列出相应的等式或不等关系式;第五,化简计算;最后定量分析结果的物理含义。
三、数学中向量分解原则与物理中矢量分解原则的区别
数学中向量的分解要求是只要选定一组基底即可,同一向量所选基底不同,分解结果也就不同,但都是正确的。而物理中矢量的分解一般具有唯一性条件,其原则是由矢量所产生的效果或由问题的需要来确定分解的方向,即按照“效果或需要”来分解是矢量分解的基本原则。
例如,在倾斜角为α的斜面上放置一块质量为m的木块,木块静止在斜面上,则重力mg所产生的效果,既有使木块沿斜面下滑的趋势,又有对斜面产生的压力,所以对重力进行分解时,应沿平行斜面和垂直于斜面两个方向来分解,如图14,得到的两个分力分别是mgsinα和mgcosα。
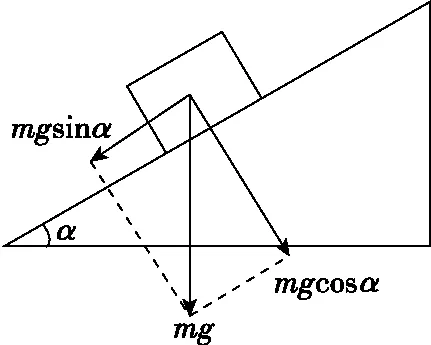
图14
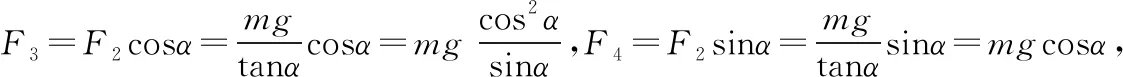
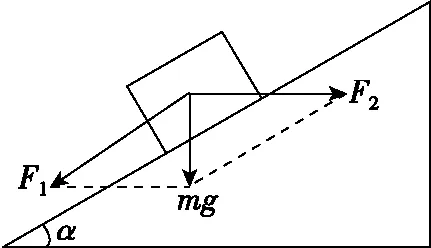
图15
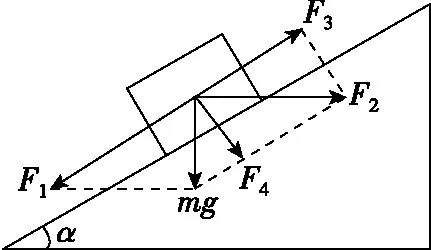
图16
【例4】如图17所示,小船在绳的牵引作用下匀速前进,假设水的阻力不变,试分析小船在靠岸的过程中,所受浮力和绳的拉力如何变化的。
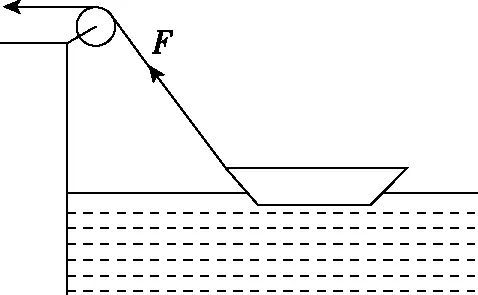
图17
【解法1】小船所受的力包括重力G、绳子的拉力F、向上的浮力Q和水的阻力f。由于小船匀速前进,则四力处于平衡状态,且f和G为恒力。
设绳子和水平方向的夹角为α,如图18所示,则有
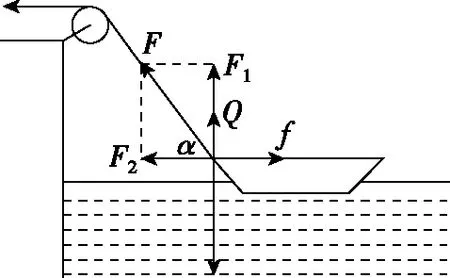
图18
Fcosα=f
①
Fsinα+Q=G
②

【解法2】依据解法1的受力分析,可知四力构成了封闭的矢量图,如图19所示,在小船靠岸的过程中,角α逐渐增大,拉力F会逐渐增大(由F1到F2),而竖直向上的浮力Q逐渐减小(由Q1向Q2)。
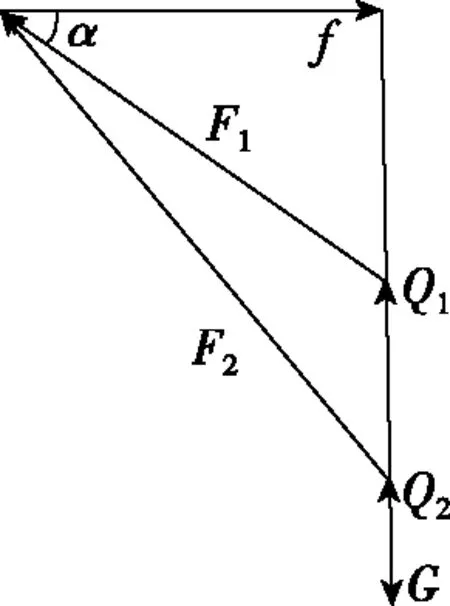
图19
【例5】如图20所示,小船在绳的牵引作用下前进,假设水的阻力不变,绳子以恒定的速度v0收缩使小船靠岸,求小船的速度v。
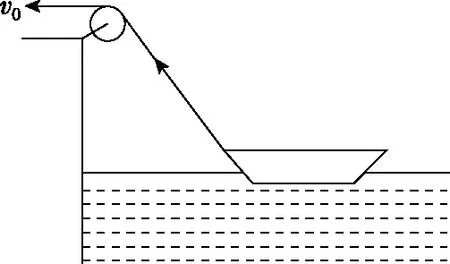
图20
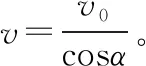
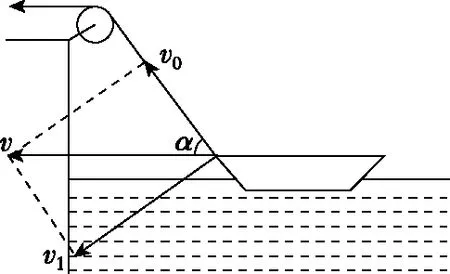
图21
【点评】学生对例4与例5的矢量分解最容易混淆,例4中绳子的拉力、浮力、阻力及船的重力处于平衡状态,合力F被分解为沿竖直和水平方向的两个分力,但在例5中,好多同学误把绳子的收缩速度当成了船实际的运动速度而分解为沿竖直和水平方向的两个分速度,如图22所示,这反映出学生缺乏对各分量做必要的物理意义分析的能力,如果船有竖直向上的分速度,那么船就会腾空而起,这显然是不正确的。所以在教学中有必要提醒学生要注意各矢量的分解是否符合实际意义,也要辨析清楚物体实际运动速度才是运动的合速度。
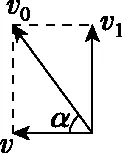
图22
四、向量的坐标法在物理中的应用
【例6】已知两个力(单位:N)F1与F2的夹角为60°,其中F1=(2,0),某质点在这两个力的共同作用下,由点A(1,1) 移动到点B(3,3)(单位:m)。
(1)求F2;
(2)求F1与F2的合力对质点所做的功。
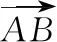
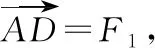
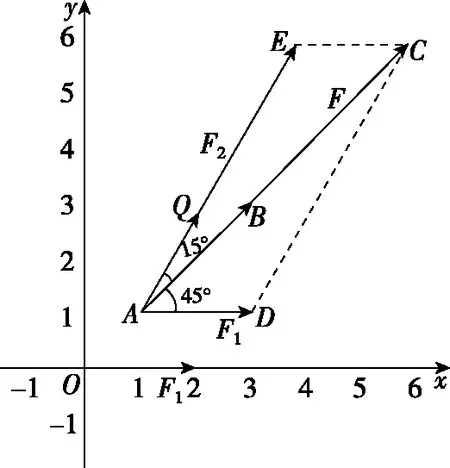
图23
所以有y=x+2
①
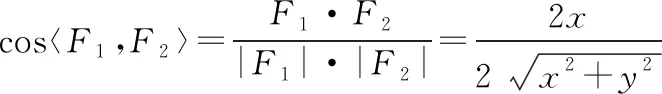
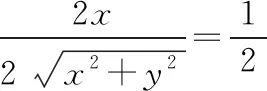
②

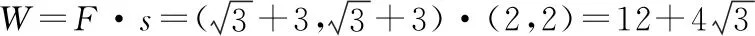
【解法2】(1)依照题意和图23所示,|F1|=2,在△ADC中,∠D=120°,∠DCA=15°
【点评】本题的关键一是要知道力F1的大小和方向,且与另一个力F2的夹角和合力方向,利用向量加法的平行四边形法则做出矢量合成图示;二是在求值方法的选取上,因为力F1是用向量坐标表示的,可选取向量坐标法来解,也可以选用正弦定理来解。以上两点体现了数学与物理两学科在相对应知识点上的一致性。本题的解题方法和作图步骤,有利于培养学生用数学思维和方法解决物理问题的意识和能力。
以上各例题有多种解法,每种解法所用的数学知识侧重点不同,从不同的角度思考和解决同一物理问题,既能提高学生物理的解题能力,又能培养学生数学应用意识和能力,更能为学生树立起数理是一家的观念,进而培养学生用数学思维与方法思考物理问题的意识。
