基于响应面法的聚丙烯纤维再生砖骨料混凝土配合比优化

2022-08-29黄炜郭余婷葛培权文立董昆仑

中南大学学报（自然科学版） 2022年7期

黄炜，郭余婷，葛培，权文立，董昆仑

(西安建筑科技大学土木工程学院，陕西西安，710055)

随着城市化进程的加速，一大批老旧建筑将会被拆除，必然会产生大量的建筑垃圾。建筑垃圾主要包括废弃混凝土及废弃砖，其中废弃砖占35%～45%[1-3]。采用废弃碎砖部分或全部代替天然骨料来制备再生砖骨料混凝土(RBAC)，不仅可以解决建筑垃圾的堆放及填埋问题，还能节约自然资源、保护环境[4-5]。但由于再生砖骨料(RBA)存在表面粗糙、孔隙率大、自身强度低、吸水率高等缺陷，其工程应用范围受限[6]。为扩大RBAC应用范围，需对其性能进行全面和系统的研究，而配合比设计直接决定了再生混凝土的工作性能、力学性能和耐久性，是性能研究的前提条件[7-8]。

目前，有关RBAC 配合比优化设计的研究尚少，人们大多参照“普通混凝土配合比设计规程”[9]进行配合比设计，并利用正交试验寻求最优配比。但采用正交试验寻求最优配比时，考虑因素间的相互作用，会导致工作量较大，且无法在指定的区域获得因素与响应值之间明确的函数关系[10-11]。响应面法(RSM)是数学与统计学相结合的产物，能用少量试验数据建立多个因素与一个或多个响应值之间的数学模型，并评估各因素间的交互作用对响应值的影响，确定最优响应值，与正交试验相比具有试验次数少、成本低、精度高等优势[12]。

此前，RSM 多用于化学、生物、农业及食品领域，近年来开始应用于建筑材料领域中水泥砂浆和混凝土的配合比优化。吕官记等[13]通过RSM的Box-Behnken 设计(BBD)模式建立二次多项式回归方程，进而得出三元聚合物砂浆三因素三响应值的综合最优配比。王静文等[14]利用RSM 的中心复合设计对玄武岩纤维泡沫混凝土进行试验设计，并结合渴求函数对玄武岩纤维泡沫混凝土实现多目标优化。ZHANG 等[15]通过RSM 的BBD 模式设计得到再生骨料透水混凝土的最优骨料级配和外加剂用量。上述研究表明将RSM 应用于建筑材料配合优化具有显著优势，但应用RSM 进行RBAC的相关研究较少。

本文作者以水灰比、再生砖骨料取代率和聚丙烯纤维(PPF)体积分数为因素，以聚丙烯纤维再生砖骨料混凝土(PPFRBAC)抗压强度、劈裂抗拉强度为响应值，在正交试验的基础上利用RSM 建立响应面模型，分析各因素对响应值的影响，结合渴求函数获得PPFRBAC的最优配比，以期为纤维再生砖骨料混凝土配合比多目标优化提供参考。

1 响应面法

典型的二阶响应面设计包括全因子设计(FFD)、中央复合设计(CCD)和BBD。其中，FFD需要大量的试验数据且模型的精确性低，所以应用较少。CCD和BBD均可用于三因素的试验设计及评估因素之间的非线性关系，且预测精度高，应用较广泛。但BBD 不需要连续进行多次试验，并且在因素相同的情况下，BBD 的试验次数比CCD的少。此外，由于BBD限制了试验中的因素水平(高、中、低水平的编码值分别为1，0，-1)，因素的变化不会超过安全范围，所以BBD 具有更明显的优势。综合考虑试验组数和因素水平，本文采用响应面法(RSM)的BBD来建立回归模型。

RSM 采用多项式回归方程来拟合因素与响应值之间的函数关系，主要包括收集试验数据、建立响应面模型、检验模型、优化最佳参数和验证最佳参数5个步骤[16]。式(1)所示为包含常数项、一次项、交互项和二次项的多项式响应曲面数值模型：

式中：Y为响应值；β0为常数项；xi和xj为独立变量；βi为一次项系数；βii为二次项系数；βij为交互项系数；ε为随机误差；n为变量数。

RSM 中的方差分析可以确定预测模型的一次项、交互项和二次项的影响以及模型回归系数，还可以用于评估模型的显著性和可信度。采用相关系数R2和调整系数评估模型的可靠性。

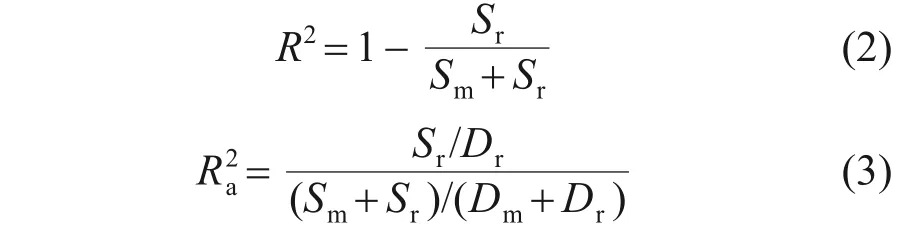
式中：Sr为残差平方和；Sm为回归平方和；Dr为残差自由度；Dm为回归自由度。

Design-expert 10.0.7 软件具有基于渴求函数的数值优化功能，可同时获得最优变量值和响应值。渴求函数(D)为各响应渴求值的幂指数乘积，其取值范围为0～1，D越接近1，所得到的最优条件将更可靠。单个响应的渴求值(di)和渴求函数表达式式分别为：

式中：Yi为第i个响应的拟合值；L为第i个响应的下限值，U为第i个响应的上限值；wi为第i个响应的权重。

本文通过9组试验数据建立如式(1)所示的响应曲面回归方程，随后通过式(2)和式(3)对回归方程的可信度进行评价，最后结合式(4)选取最优配比。

2 试验概况

2.1 试验材料

水泥采用“秦岭牌”普通硅酸盐水泥，强度等级为32.5。天然细骨料采用细度模数为2.8 的普通河砂。粗骨料分为天然粗骨料和再生粗骨料，天然粗骨料采用粒径为5～20 mm的连续级配碎石；再生粗(砖)骨料由陕西建新环保科技发展有限公司生产，其物理性能见表1，粗骨料的颗粒级配见表2。聚丙烯纤维由上海影佳实业发展有限公司生产，其物理性能见表3。

表1 再生粗骨料物理性能Table 1 Physical properties of recycled coarse aggregate

表2 粗骨料颗粒质量分数Table 2 Particle mass fraction of coarse aggregate %

表3 聚丙烯纤维物理性能Table 3 Physical properties of polypropylene fiber

2.2 试验设计

参照“普通混凝土配合比设计规程”进行PPFRBAC 配合比设计[9]。试验用水量为固定值，研究水灰比、再生砖骨料取代率和聚丙烯纤维体积分数对PPFRBAC抗压强度、劈裂抗拉强度的影响。本文作者分别选取水灰比(因素A)、再生砖骨料取代率(因素B)和聚丙烯纤维体积分数(因素C)这3个因素，在L9(33)三因素三水平正交试验基础上，利用Design-expert 10.0.7 软件中的BBD 设计功能对试验数据进行处理。基于已有的研究并考虑试配可行性等，确定各水平的具体范围，试验因素与水平见表4。

表4 试验因素与水平Table 4 Factors and level of the test

2.3 试件制备及试验方法

依据“普通混凝土力学性能试验方法”[17]进行力学试验。首先，将混凝土搅拌机进行挂浆处理，接着向搅拌机中加入称量好的水泥、砂、碎石、再生砖骨料和聚丙烯纤维，干拌30 s，然后加水搅拌120 s。待PPFRBAC拌和均匀后，将其倒入事先涂抹过脱模剂的试模内，并利用振捣棒进行振捣，振捣时应避免过振和漏振，以防混凝土离析及降低纤维与基体的黏结强度。随后用抹刀将试件抹平，并在试模上贴上标签，24 h后脱模。最后，将试件放在养护池中，参照“纤维混凝土应用技术规程”[18]养护28 d。采用边长为150 mm 的立方体试件进行抗压强度和劈裂抗拉强度试验，加载设备为TYA-2000型电液式压力试验机。

3 结果及分析

3.1 试验结果

PPFRBAC 的抗压强度、劈裂抗拉强度实测值与预测值如表5所示。

3.2 模型的建立及方差分析

利用Design-expert10.0.7 软件对表5 中的试验数据进行回归拟合分析，分别得到抗压强度和劈裂抗拉强度的响应曲面拟合方程Y1和Y2：

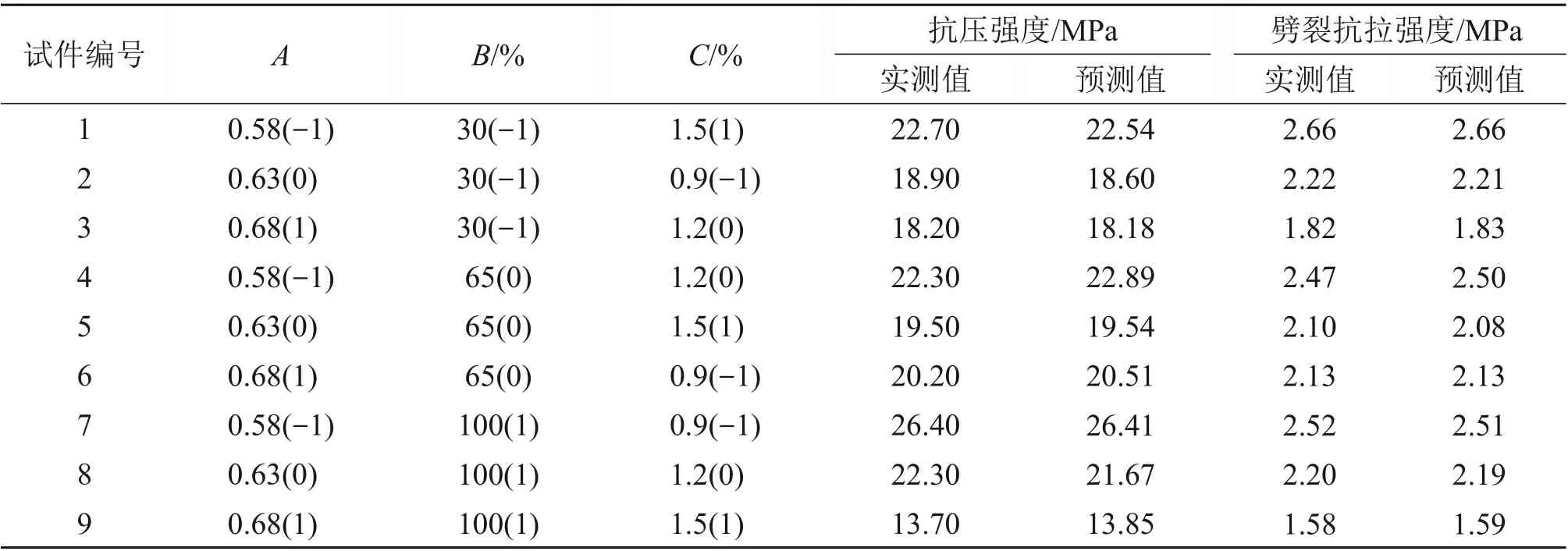
表5 试验设计与结果Table 5 Test design and results

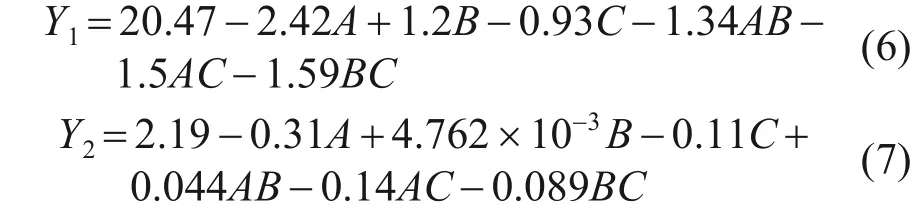
由式(6)和式(7)可知：在一定范围内，RBAC抗压强度、劈裂抗拉强度与水灰比、PPF体积分数呈反比，与RBA取代率呈正比。

对上述回归模型进行方差分析和可信度分析，结果分别如表6～8所示。本文采用P值对模型显著性进行评价，采用相关系数R2、调整系数、变异系数和信噪比对模型可信度进行综合评价。P值表示原假设出现的概率，F值越大，P值相应越小，表明模型的显著性越高[19]。当P值大于0.05时，模型显著性较低，不具有统计学意义，回归模型不可用；反之，回归模型显著性较高[20]。相关系数R2表示响应值与真值间的差异程度，取值范围为0～1，其值越大，表明两者的差异性越小。调整系数与相关系数R2差值越小，变异系数越小，且信噪比大于4，说明回归方程拟合程度越高，试验的可信度和精度越高。

由表6 和表8 可知：抗压强度回归模型Y1的P值为0.029，F值为34.19，说明回归模型的显著性较高；同时，相关系数R2为0.990，调整系数为0.961，变异系数为3.42%，信噪比为20.368，说明回归模型具有较高的可靠性。此外，单因素A的P值小于0.05，说明单因素A对抗压强度的作用显著，单因素B和C以及双因素AB，AC和BC的P值均大于0.05，说明这5个因素的影响较小。

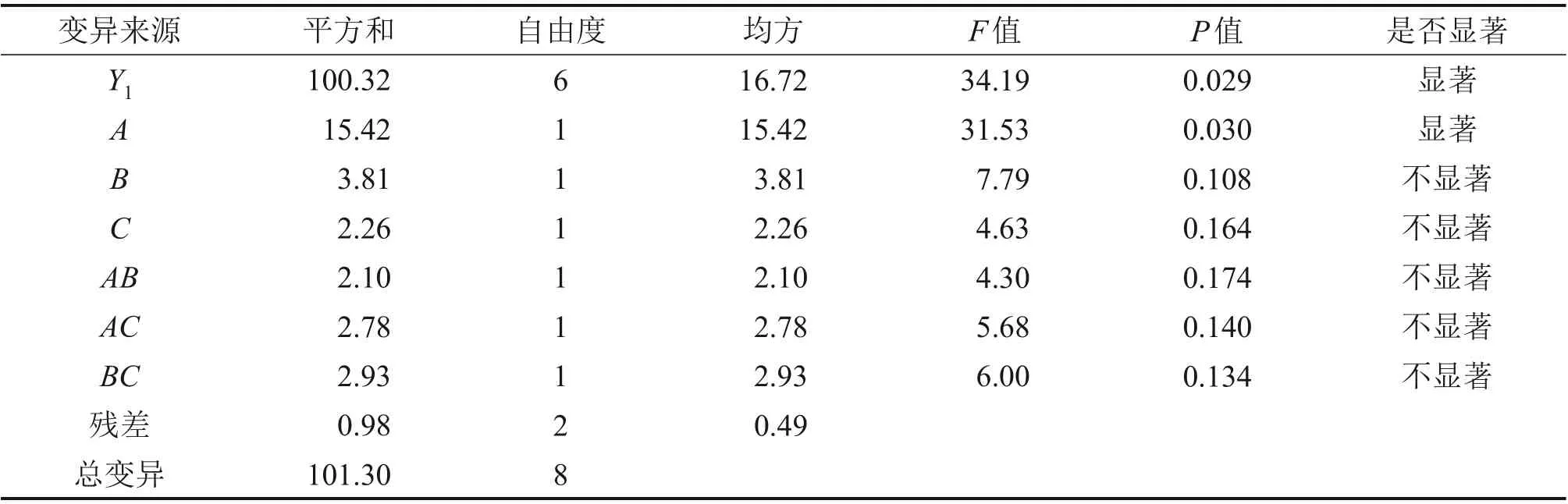
表6 抗压强度回归模型方差分析Table 6 Variance analysis of compressive strength regression model

表8 模型可信度检验分析Table 8 Reliability test and analysis of the model

由表7和表8可知：劈裂抗拉强度回归模型Y2的P值为0.005，F值为183.20，说明回归模型的显著性极高；同时，相关系数R2为0.998，调整系数为0.993，变异系数为1.33%，信噪比为41.807，说明回归模型可靠性较高。此外，因素A，C和AC的P值均小于0.05，说明单因素A和C以及双因素AC对劈裂抗拉强度的影响较显著，且按影响程度从大到小排序依次为A，C和AC；因素B，AB和BC的P值均大于0.05，说明这3 个因素的影响较小。

表7 劈裂抗拉强度回归模型方差分析Table 7 Variance analysis of regression model for splitting tensile strength

运用Design-expert 10.0.7 软件的ANOVA 功能可以导出回归模型的学生化残差。学生化残差是残差除以标准差后得到的数值，用以直观地判断残差项是否服从正态分布。学生化残差可由普通残差导出，在回归模型诊断中具有十分重要的作用[21]。抗压强度和劈裂抗拉强度回归模型的学生化残差分别如图1和图2所示。由图1和图2可知：回归模型均不存在异常数据点，数据点均匀地分布在直线附近，说明残差较小，模型的拟合效果较理想。

图1 抗压强度回归模型的学生化残差Fig.1 Student residual of compressive strength regression model

图2 劈裂抗拉强度回归模型的学生化残差Fig.2 Student residual of splitting tensile strength regression model

3.3 响应面分析

根据线性回归模型分别绘制抗压强度和劈裂抗拉强度的3D响应曲面图及对应的等高线图，用以直观分析两因素交互作用对再生砖骨料混凝土抗压强度和劈裂抗拉强度的影响，结果分别如图3和图4所示。

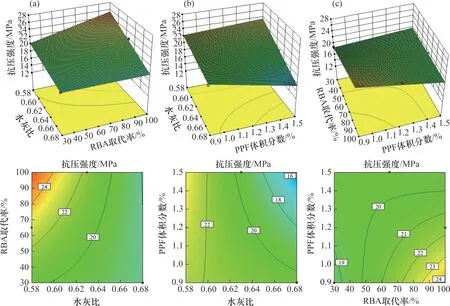
图3 抗压强度响应曲面图及等高线图Fig.3 Response surface plots and contour diagram of compressive strength

3.3.1 抗压强度分析

由图3(a)可知：当PPF体积分数为1.2%，RBA取代率小于等于60%时，抗压强度随水灰比增大而无明显变化；而当RBA 取代率高于60%时，抗压强度随水灰比增大而降低。当水灰比小于等于0.63 时，抗压强度随RBA 取代率增大而升高；而当水灰比高于0.63 时，抗压强度随RBA 取代率增大而无明显变化。由图3(b)可知：当RBA 取代率为65%，水灰比小于等于0.63时，抗压强度随PPF体积分数增大而无明显变化；而当水灰比高于0.63时，抗压强度随PPF体积分数增大而降低。当PPF体积分数小于等于1.2%时，抗压强度随水灰比增大而无明显变化；而当PPF体积分数高于1.2%时，抗压强度随水灰比增大而降低。由图3(c)可知：当水灰比为0.63，PPF 体积分数小于等于1.2%时，抗压强度随RBA 取代率增大而升高；而当PPF 体积分数高于1.2%时，抗压强度随RBA取代率增大而无明显变化；当RBA 取代率小于等于60%时，抗压强度随PPF体积分数增大而无明显变化；而当RBA 取代率高于60%时，抗压强度随PPF 体积分数增大而降低。

综上分析可知，低水灰比和高RBA 取代率、低水灰比和高PPF 体积分数以及高RBA 取代率和低PPF体积分数均可使PPFRBAC抗压强度增大。

3.3.2 劈裂抗拉强度分析

由图4(a)可知：当PPF体积分数为1.2%，水灰比固定不变时，劈裂抗拉强度随RBA 取代率增大而无明显变化；当RBA 取代率固定不变时，劈裂抗拉强度随水灰比增大而降低。由图4(b)可知：当RBA取代率为65%，PPF体积分数固定不变时，劈裂抗拉强度随水灰比增大而降低；当水灰比小于等于0.63时，劈裂抗拉强度随PPF体积分数增大而无明显变化，而当水灰比高于0.63 时，劈裂抗拉强度随PPF 体积分数增大而降低。由图4(c)可知：当水灰比为0.63，PPF 体积分数小于等于1.2%时，劈裂抗拉强度随RBA 取代率增大而升高，而当PPF 体积分数高于1.2%时，劈裂抗拉强度随RBA取代率增大而无明显变化。当RBA 取代率小于等于60%时，劈裂抗拉强度随PPF 体积分数增大而无明显变化；而当RBA 取代率高于60%时，劈裂抗拉强度随PPF体积分数增大而降低。

图4 劈裂抗拉强度响应曲面图及等高线图Fig.4 Response surface plots and contour diagram of splitting tensile strength

综上分析可知，低水灰比和低RBA 取代率、低水灰比和高PPF 体积分数以及高RBA 取代率和低PPF 体积分数均可使PPFRBAC 劈裂抗拉强度增大。

3.4 PPF增强RBAC劈裂抗拉强度机理分析

由响应面分析结果可知PPF增强RBAC劈裂抗拉强度机理如下：

1) 均匀而任意分布的PPF 在硬化过程中改变了RBAC 内部结构，使RBAC 的内部缺陷减少，提高了材料的连续性。在受到外力作用时，PPF与RBAC共同受力变形，PPF的牵连作用使RBAC裂而不断并能进一步承受荷载，从而提高RBAC 劈裂抗拉强度。

2)RBA 表面粗糙且多棱角，同时表面黏附有硬化的水泥砂浆，有利于其与PPF之间产生较大的摩擦力和机械咬合力，在受力时能有效地阻止纤维被拔出。因此，在RBAC加入适量的PPF有利于提高其整体强度。

3.5 模型的多目标优化与验证

在回归模型的基础上，结合渴求函数对PPFRBAC 进行多目标优化，优化目标为在3 种不同水灰比(因素A)下寻求最优的聚丙烯纤维体积分数(因素B)和再生骨料取代率(因素C)以同时获得PPFRBAC 抗压强度回归模型(Y1)和劈裂抗拉强度回归模型(Y2)的最大值。优化设计目标如表9所示。

将表9 所定义的目标输入Design-expert 10.0.7软件中，得出水灰比为0.58，0.63和0.68时的最优配比以及抗压强度和劈裂抗拉强度的最大值，见表10。由表10 可知：若想获得较高的强度，则需将水灰比控制在较小值；若考虑经济性，则需将水灰比控制在较大值，即水泥用量较小。

表9 PPFRBAC优化设计目标Table 9 Optimization design objectives of PPFRBAC

为进一步验证模型的精确性，对表10所示的3组配合比进行试验验证，并将强度试验值与预测值进行对比，结果如表11 所示，使用相对误差绝对值进行验证，计算公式[19]如下：

表10 响应面设计最优设计结果Table 10 Optimal design results of response surface design

式中：E为相对误差绝对值；VT为抗压强度或劈裂抗拉强度试验值；VP为抗压强度或劈裂抗拉强度预测值。

由表11 可知：在Ⅰ，Ⅱ和Ⅲ组配合比下，抗压强度试验值与预测值之间的相对误差绝对值分别为2.5%，2.8%和3.4%，均小于5%，说明抗压强度回归模型的预测精度较高。在Ⅰ，Ⅱ和Ⅲ组配合比下，劈裂抗拉强度试验值与预测值之间的相对误差绝对值分别为2.9%，3.0%和2.7%，均小于5%，说明劈裂抗拉强度回归模型的预测精度较高[22]。因此，通过RSM 优化PPFRBAC 配合比，可提高试验效率，从而获得力学性能较好的PPFRBAC。