基于概率密度演化理论的磁浮列车-轨道梁耦合系统随机动力分析

余志武，张鹏，丁叁叁，单智

(1. 中南大学土木工程学院，湖南 长沙，410075；2. 中南大学 高速铁路建造技术国家工程实验室，湖南 长沙，410075；3. 中车青岛四方机车车辆股份有限公司，山东 青岛，266111)

磁浮列车有着低噪声、低排放、低维护成本、无脱轨风险等优点，正成为一种新型的轨道交通工具在全世界范围内被广泛接受。磁浮车桥耦合振动是磁浮交通面临的一项关键技术问题[1]，国内外学者针对该问题开展了相关研究[2-7]，主要包括计算模型的研究和控制算法的研究。CAI等[8]以集中力和2自由度簧上质量模型简化磁浮车辆，分析了不同车速对桥梁动力响应的影响。滕延锋等[9]将车辆视为移动均布荷载，对磁浮列车通过三跨连续型轨道梁时的耦合振动反应进行了确定性参数分析。ZHAO等[1]建立了考虑10自由度磁浮车辆的垂向耦合系统模型，将复杂的电磁力模型简化为弹簧-阻尼模型，分析了磁浮车辆在不同类型轨道梁上运行的走行性能。YANG 等[10-13]采用比例-积分-微分(PID)算法、状态最优估计算法、鲁棒算法、神经网络算法等不同控制算法计算有源主动控制电磁力，对大量参数进行了分析。以上研究都是确定性分析或者采用1条或几条轨道不平顺激励来计算系统动力响应，无法准确考虑随机激励引起的系统响应的离散程度。而实际上，磁浮系统是复杂的随机系统，随机轨道不平顺、车桥系统结构参数和多重外荷载随机源的存在使得系统的随机动力特性更加难以估计[14]。经典的Monte Carlo 法(MCM)由于需要大量的样本来保证计算精度，限制了人们使用该方法对车桥振动特性进行研究。目前采用随机振动理论对磁浮车桥耦合系统进行的研究有限。概率密度演化理论是近年来发展的随机动力分析方法，被广泛应用于地震工程、风工程、建筑工程等领域，利用该方法考虑随机轨道不平顺和随机结构参数是合理、可行的[15]，能得到高精度的系统响应均值、标准差及概演率密度演化曲线[16]。迄今为止，尚未见将该方法应用于磁浮车桥耦合振动分析的案例。为此，本文作者建立磁浮车辆-控制器-轨道梁耦合系统时变随机动力分析模型，运用数论选点法选取N-维代表性点集和随机谐和函数法模拟轨道不平顺，将概率密度演化理论引入磁浮动力分析系统。以常导型磁浮列车通过三跨连续型轨道梁为例，计算车桥动力响应的均值、标准差和概率密度演化曲线，采用Monte Carlo 法和文献结果验证模型的计算效率和精度，计算不同概率保证率的行车速度和支座刚度对系统响应的影响规律。

1 磁浮列车-轨道梁耦合系统模型

1.1 磁浮车辆模型

磁浮列车模型每节车辆由1节车体和4个磁转向架组成[17]，如图1所示。由于列车移动时对轨道梁的垂向激扰远大于横向激扰，因此，只考虑车桥的垂直平面内振动。考虑车体(zc,βc)及磁转向架(zbi,βbi,i= 1,…,4)浮沉和点头运动，每节车辆具有10 个 自 由 度，Uv=[zc,βc,zb1,βb1,zb2,βb2,zb3,βb3,zb4,βb4]。每车采用16 个集中电磁力(Fi,i=1, 2,3,…,16)模拟均匀分布的电磁作用力以兼顾计算精度和效率[17]。假定车体和磁转向架均为刚体，各刚体间通过线性弹簧-阻尼器连接。根据弹性系统总势能不变原理的“对号入座”法则[18]，经推导得到列车运动方程：

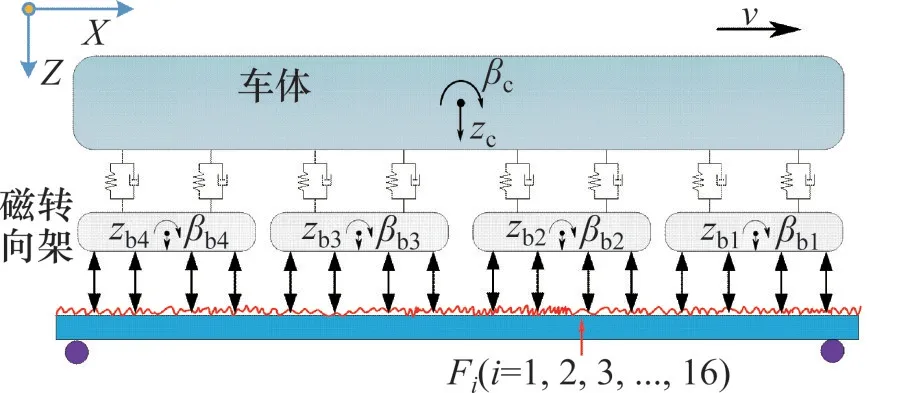
图1 磁浮列车-轨道梁垂向耦合系统模型Fig.1 Interaction model of maglev vehicle-guideway

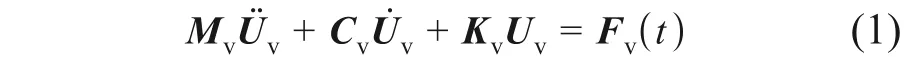
式中：Mv，Cv，Kv和Uv分别为车辆的整体质量矩阵、阻尼矩阵、刚度矩阵和位移向量；Fv(t)为车辆外荷载向量；U̇v和Üv分别为速度向量和加速度向量。

1.2 连续型轨道梁模型

建立轨道结构的方法通常有模态叠加法和有限元法，以往的研究常采用模态叠加法建立桥梁动力方程以降低计算量[18]。采取有限元法建立轨道结构时，可避免用模态叠加法选取有限阶模态时难以全面考虑轨道结构振动状态的问题。连续梁中支座数量较简支梁多，建立考虑弹性支座[5]的轨道梁模型以考虑连续梁中支座刚度影响，轨道梁系统的有限元法动力方程为

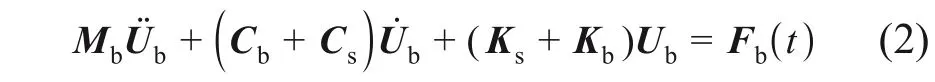
式中：Mb，Cb，Kb和Ub分别为轨道梁系统的初始质量矩阵、阻尼矩阵、刚度矩阵和自由度向量；Fb(t)为轨道梁系统外荷载向量；Cs和Ks分别为支座阻尼和刚度。

阻尼可按Rayleigh阻尼确定，其中，

1.3 悬浮控制模型

磁浮车辆通过悬浮控制系统实现车辆的稳定悬浮，单个电磁铁是控制系统中最基本的控制单元，建立单个电磁铁与轨道梁相互作用模型，如图2 所示。忽略电磁绕组的磁通漏和磁势的损失，假定磁势在悬浮间隙上均匀分布，其瞬时垂向悬浮电磁力为

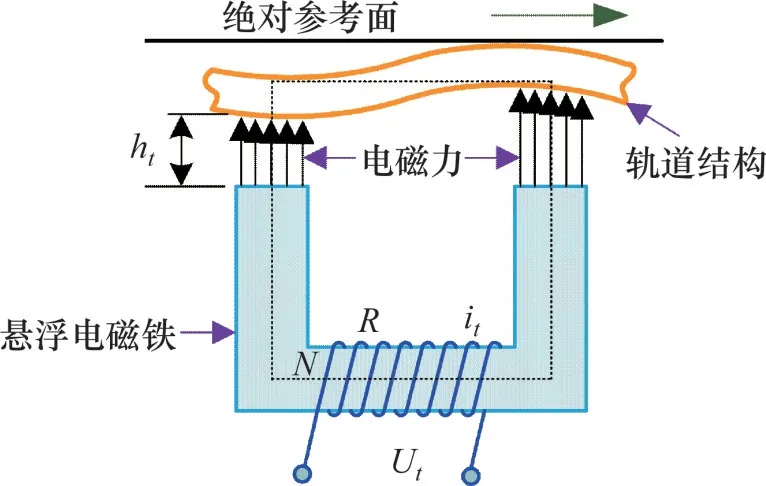
图2 单个电磁铁-轨道梁相互作用示意图Fig.2 Interaction model of single electromagnetguideway

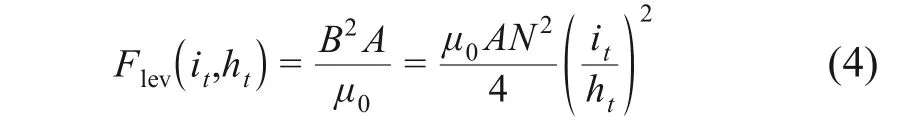
式中：it为实时电流；ht为实时悬浮间隙；B为磁通密度；μ0为磁导率；A为磁极面积；N为电磁绕组匝数。

由于常导磁浮开环控制本质上具有不稳定性，须引入反馈控制使之稳定悬浮[17]。采用工业控制中广泛使用的PID控制算法，以电流控制实现闭环反馈控制，将悬浮间隙、电磁铁速度和加速度作为状态反馈控制量，其算法原理为

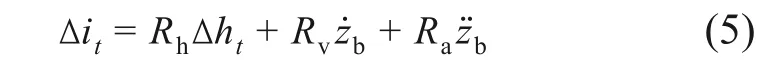
式中：Rh，Rv和Ra为反馈控制增益；żb和z̈b分别为t时刻的电磁铁垂向速度和加速度；Δht为t时刻悬浮间隙相对平衡位置变化量，Δht=ht-h0；Δit为t时刻电流变化量，Δit=it-i0。

1.4 轨道不平顺随机模拟

轨道不平顺是引起磁浮车桥耦合振动的主要激励源之一，对磁浮列车运行安全和平稳具有重要影响[1]。采用磁浮功率谱密度函数[19]：

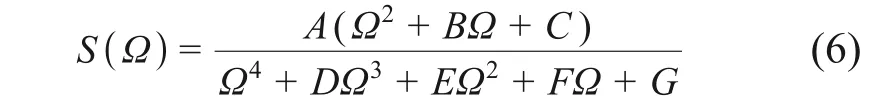
式中：S(Ω)为不平顺功率谱密度函数；A，B，C，D，E，F和G为谱相关系数；Ω为空间频率。

采用随机谐和函数法描述随机轨道不平顺。相对于常用的三角级数法，随机谐和函数法采用少量的随机谐和函数分量即可精确模拟具有随机相位和频率的随机谐和函数过程。当随机样本功率谱精确等于目标功率谱时，可有效降低计算工作量和提高计算精度，其数学表达式为

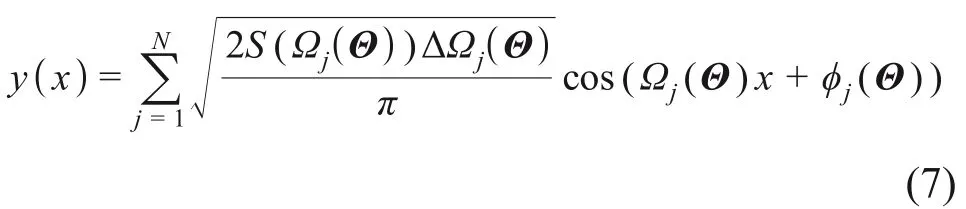
式中：S(Ωj)为轨道不平顺功率谱；ΔΩj为频率间隔带宽；Ω= 2π/λ，为空间频率；λ为轨道不平顺波长；v为列车运行速度；Ωj和ϕj分别为第j个谐和分量的圆频率和相位角，两者为相互独立的随机 变 量；ϕj服 从(0,2π]上 的 均 匀 分 布；Ωj∈[Ωmin,Ωmax]，Ωmin和Ωmax分别为频率的下限值和上限值。经仿射变换，Ωj满足Ωmin＜Ω1＜Ωj＜… ＜Ωmax。

运用数论选点法选取2N维随机向量Ωj和ϕj[20]的包含概率信息的代表性点集。根据文献[20]，由平方根序列法生成2N维超立方体点集(gp集)：

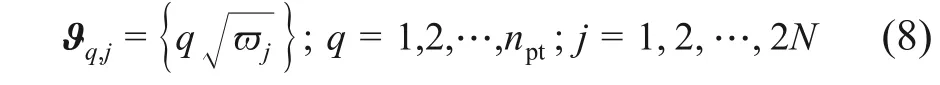
式中：ϖj为互不相同的质数；npt为样本总数。频率和波长的转换式为ω=Ωv= 2πv/λ。经仿射变换和选点变换后的代表性离散点为

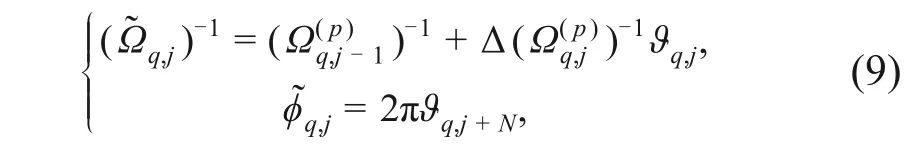
式中：j= 1,2,…,N；q= 1,2,…,npt。所有代表性点集的初始概率为PΩq= 1/npt，偏差满足d(n,pn)≤c(ϖ,ε)n-1+ε；n= 1,2,…pn，为ϑq,j构 成 的 点 集。对进行概率剖分，有

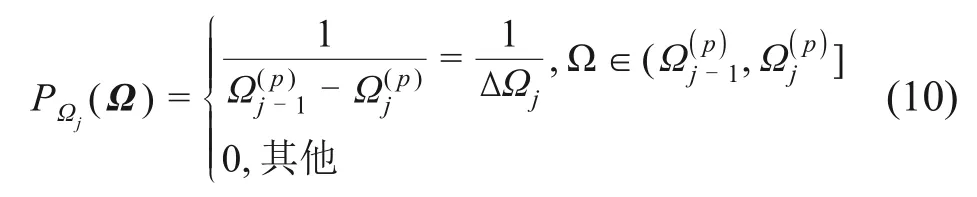
将式(10)代入式(7)，得到代表性轨道不平顺激励样本函数：

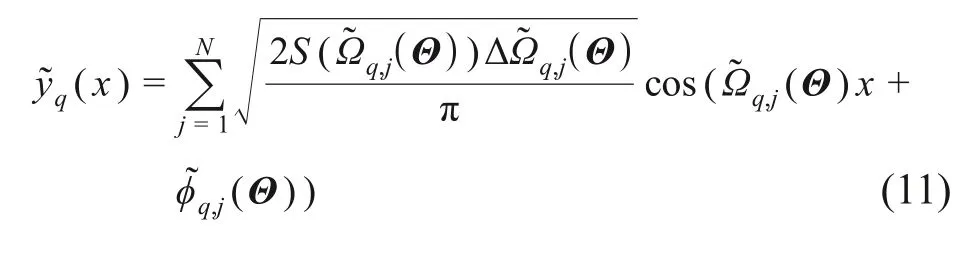
2 磁浮列车-轨道梁耦合系统时变随机运动方程

采用分离迭代方法将车辆子系统和轨道梁子系统耦联，联合式(1)和式(2)建立2 个子系统相互作用运动方程：

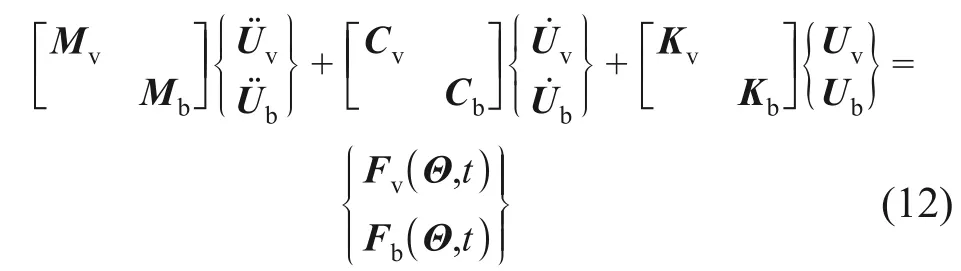
式中：随机变量集Θ=(ξ1,ξ2,…,ξs)，s为车桥系统随机变量总数目；Fv(Θ,t)为车辆系统随机外力向量；Fb(Θ,t)为轨道梁随机外力向量。

方程(12)中，车辆子系统和轨道梁子系统视为2个独立的子系统，通过车轨间的电磁相互作用力耦合作用，车辆子系统外荷载项由车辆自重和电磁力组成：

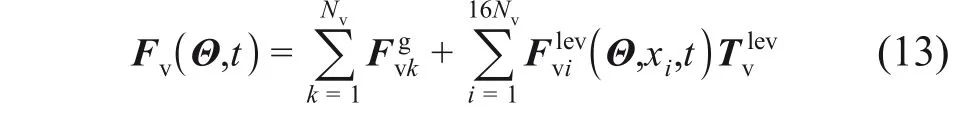
式中：Nv为列车编组数量；为第k节列车自重荷载。

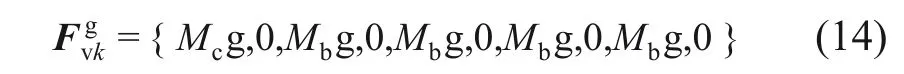
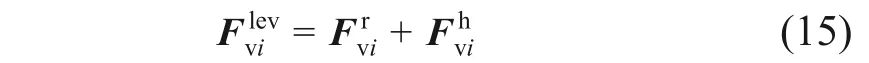
v 为车辆荷载转换向量，向量维度为1 ×Dv，Dv为 列车总自由度。Fv(Θ,t)随列车运行位置的改变而改变，具有时变特性。

车辆对轨道梁的作用力Fb(Θ,t)为

其中：δ为Dirac 函数，v为行车速度，t为运行时间；N(xi)为1 ×Db维向量，表示第i个作用点处对应的轨道梁单元的位移形函数；Db为轨道梁的自由度；和分别为作用力与反作用力。

3 概率密度演化方程的建立及求解

不失一般性，当考虑轨道不平顺的随机性时，耦合系统的整体动力方程可以表示为

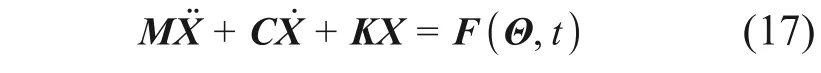
基于式(17)的车桥系统动力方程，利用Newmark-β 逐步积分法，求解给定随机变量Θ=(θ1,θ2,…,θq)(其中，q= 1,2,…,n,n为代表性样本总数)，代表性样本y͂q(x)激励下的时变随机动力方程。方程(17)的物理解答存在、唯一且连续依赖于随机参数Θ。

为表示方便，采用Z={Ψv,Ψb}T统一表示结构随机响应矩阵，则

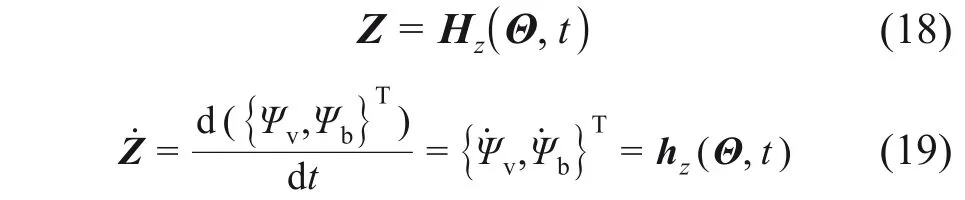
式中：Ψv和Ψb分别表示磁浮车辆和轨道梁动力响应代表函数。令U为待求解动力响应向量，则有

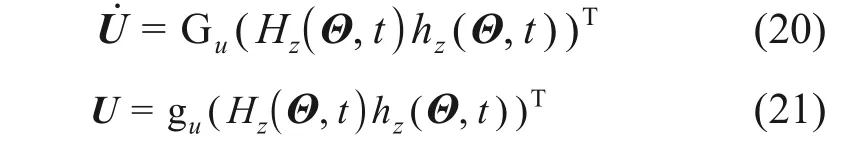
其中：gu(·)和Gu(·)为随机向量；Z=H(Θ,t)，Ż=h(Θ,t)，分别为响应U和U̇的转化方程；gu=(gu,1,gu,2,…,gu,n)T。显然，增广系统(U,Θ)是概率保守系统，满足概率守恒定律。设pUΘ(u,θ,t)为(U,θ)的联合概率密度函数，则根据概率守恒原理的随机事件描述为

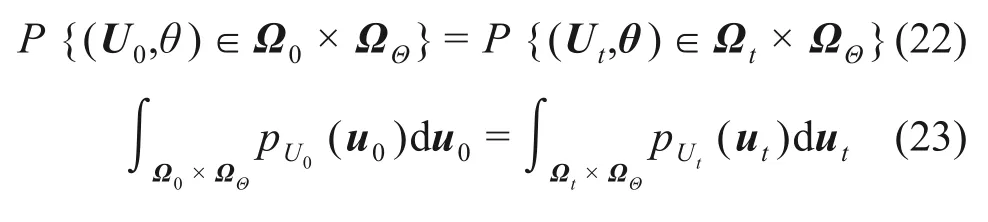
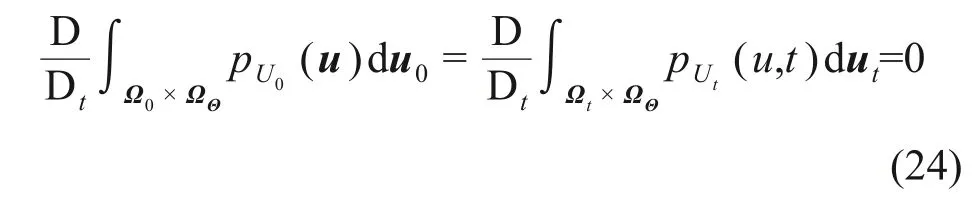
式中：P为概率函数；Ωt为初始空间区域Ω0的映射空间区域；ΩΘ为随机变量Θ的响应分布函数；为全导数公式。

将式(20)代入式(22)～(24)，建立指定随机变量的概率密度演化方程[21]：

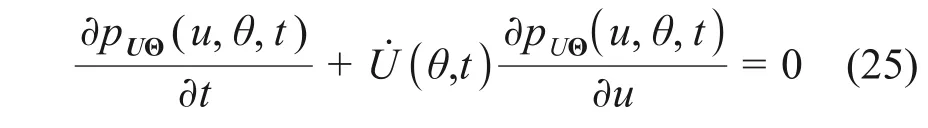
当Θ=θq(q= 1,2,3,…,n)，U(t0) =u0时，方程(25)的概率初始条件和边界条件为[21]：

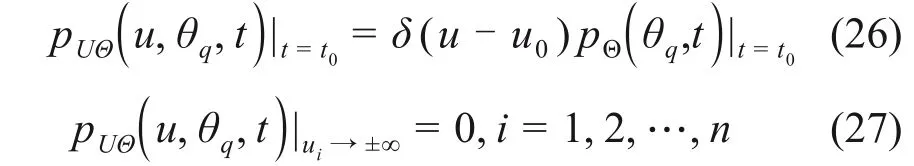
确定初始条件和边界条件后，采用带TVD 格式的双边差分法求解偏微分方程，得到概率解pUΘ(u,θ,t)，计算U(t)的概率密度函数：

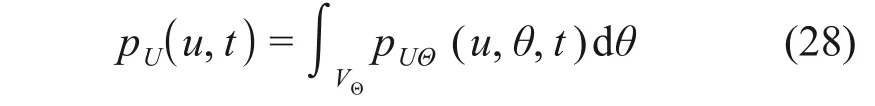
4 模型验证和随机动力数值分析

本文以三跨连续型轨道梁为例，基于MATLAB平台自主编写磁浮车辆-控制器-连续型轨道梁耦合系统随机振动分析程序。采用1.4节所述方法由目标功率谱生成轨道不平顺时域随机样本，考虑轨道不平顺中的长波和短波分量的影响，波长范围取λ∈[0.5,150]m[19]。图3 所示为代表性轨道垂向不平顺时域曲线。为方便与Monte Carlo 法对进行比，列车采用5 车编组，行车速度取100～500 km/h。磁浮车辆参数参照文献[1]取值，轨道梁参数如表1所示。轨道梁的一阶和二阶频率分别为2.46 Hz和6.09 Hz。在轨道梁两侧各添加长度为50 m 的刚性轨道，模拟列车上桥前的初始振动状态。悬浮间隙名义平衡位置取10 mm，初始电流为25 A。对于概率密度演化理论，联合数论选点的随机谐和函数法(记为PDEM-NTM)，轨道不平顺代表性频率数Nfre取500；对于Monte Carlo 法，Nfre分别取500，1 000，5 000和9 999。经概率统计计算，得到响应的均值和标准差。

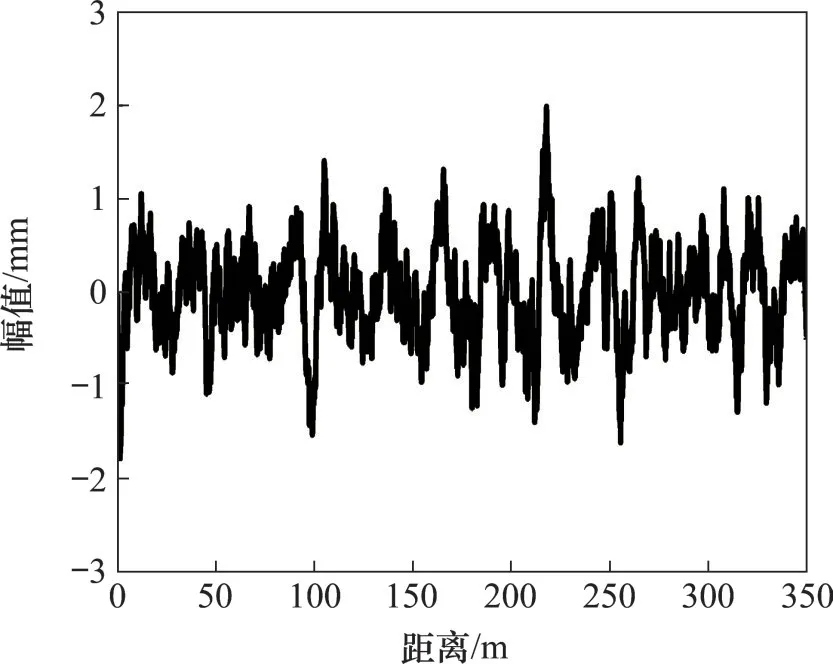
图3 代表性轨道不平顺时域曲线Fig.3 Representative vertical irregularity profile

表1 轨道梁参数取值Table 1 Parameters of guideway

4.1 计算效率和精度验证

将计算程序在相同的计算机运行并记录求解耗时。表2所示为2种方法计算耗时和标准差相对偏差对比。图4～6 中(a)和(b)所示为Monte Carlo 法和PDEM-NTM 计算结果均值和标准差时程对比。由表2 和图4～6 可知：随着所取样本数增加，Monte Carlo 法得出的响应标准差趋于稳定，并逐渐趋近于PDEM-NTM 计算结果；由PDEM-NTM计算500个样本可达到Monte Carlo法计算9 999个样本相当的精度，相对偏差最大为3.15%。Monte Carlo 法计算9 999 个样本耗时5 012.50 min，PDEM-NTM计算500个频率耗时157.12 min，相比Monte Carlo 法能提高计算效率1～2 个数量级。综上可知，PDEM-NTM 具有较高的计算精度和效率。

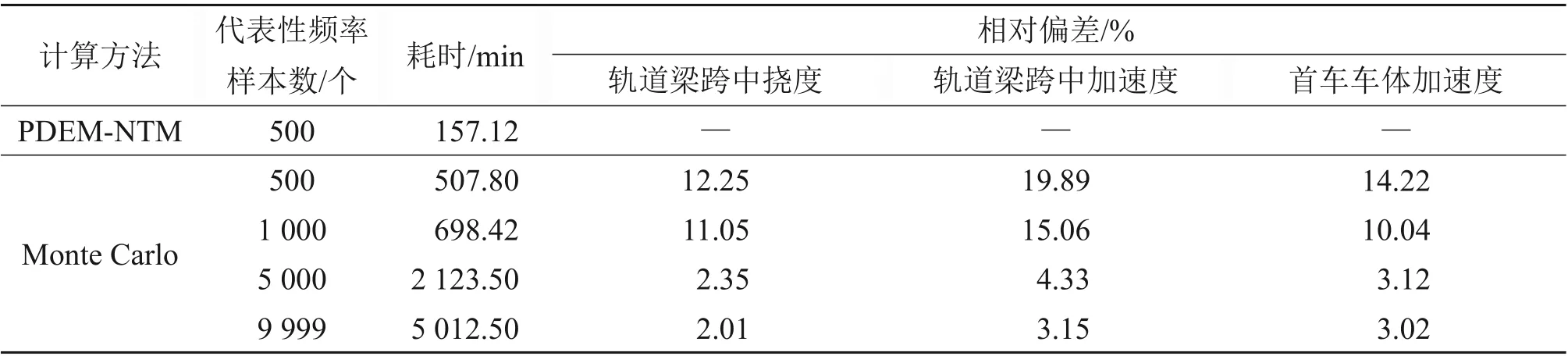
表2 计算结果对比Table 2 Comparison of calculation results

图4(c)和图4(d)所示分别为轨道梁跨中挠度的三维概率密度函数值及其等高线俯视图。分析图4(c)可知：在随机轨道不平顺激励下，轨道梁跨中挠度概率密度演化曲线形状规则且峰值单一，等概率密度演化曲线较窄，概率密度函数基本上呈标准正态分布；轨道梁跨中动挠度均值最大值为14.99 mm，对应的标准差为0.03 mm，变异系数为0.21%，这说明轨道梁动挠度受轨道不平顺影响较小，动挠度主要受车辆载重控制。文献[7]中，不考虑轨道不平顺影响时的计算挠度为15.01 mm，在本文计算的响应范围之内，这也验证了本文物理模型的正确性。

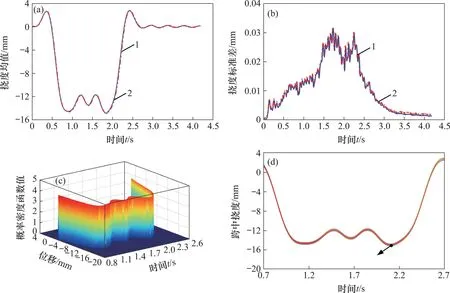
图4 轨道梁跨中挠度随机动力响应Fig.4 Random dynamic responses of guideway deflection of midpoint

图5(c)和图5(d)所示为2 种方法的首车车体竖向加速度响应的概率密度演化图及其等高线图。从图5(d)可以看出车体加速度等概率密度曲线区域宽，形状显示不规则；加速度均值最大值为0.80 m/s2，相应的标准差为0.011 m/s2，变异系数为1.38%，这说明车体加速度受轨道不平顺的影响程度大于轨道梁动挠度受轨道不平顺的影响程度。

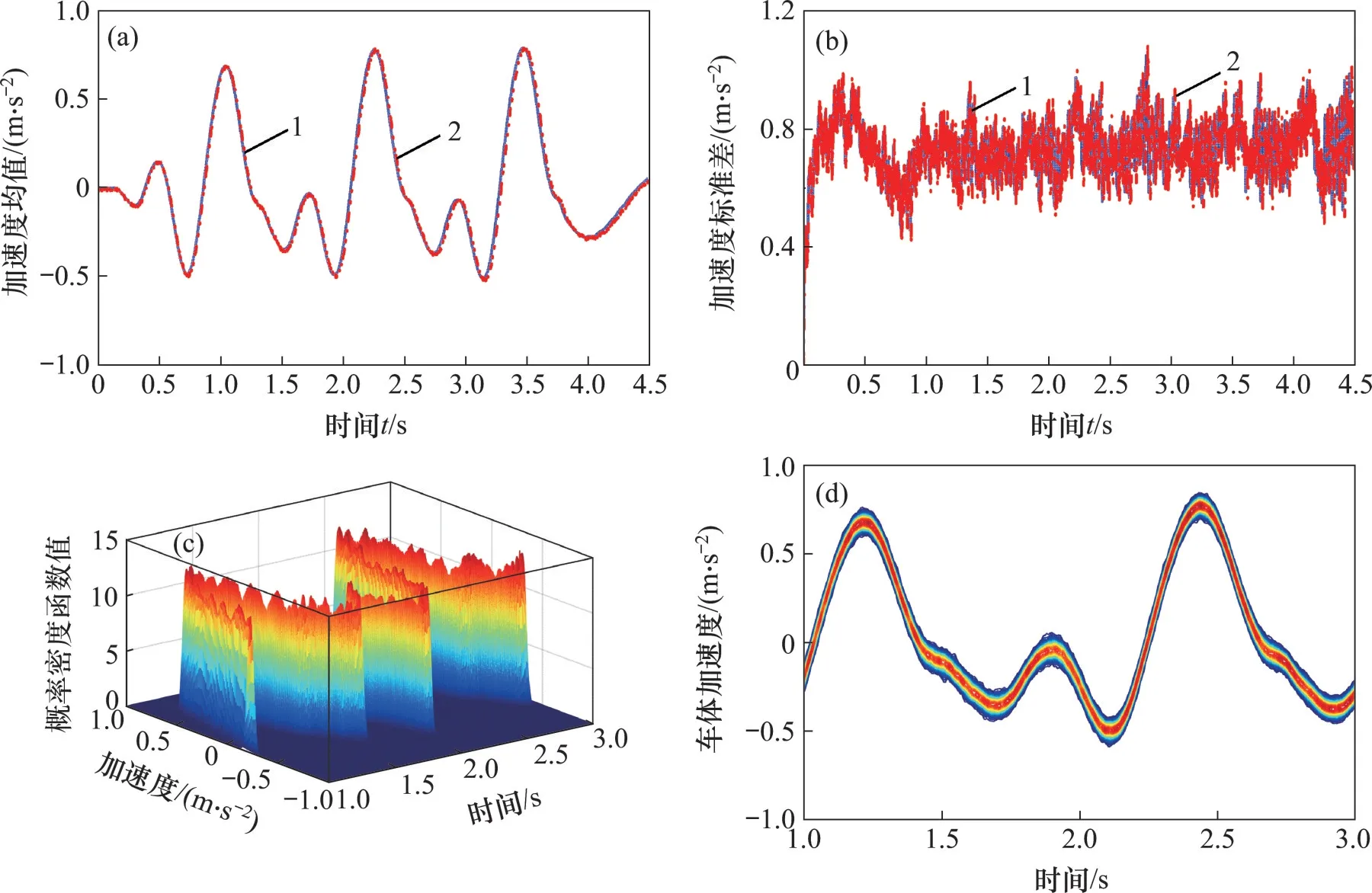
图5 首车车体加速度随机动力响应Fig.5 Random dynamic responses of the first car acceleration

图6(c)和图6(d)所示分别为轨道梁跨中加速度概率密度函数及其等高线图。分析图6(c)和图6(d)可得：轨道梁跨中加速度概率密度曲线呈现明显的演化进程和随机涨落，等概率密度曲线很不规则且值域较宽，概率密度函数多峰并呈现非标准正态分布，概率密度演化进程离散程度明显强于轨道梁跨中挠度演化进程离散程度；加速度均值最大值为0.45 m/s2，相应的标准差为0.13 m/s2，变异系数为35.13%。由此可见，轨道梁跨中加速度受轨道不平顺影响程度大于动挠度受轨道不平顺影响程度。

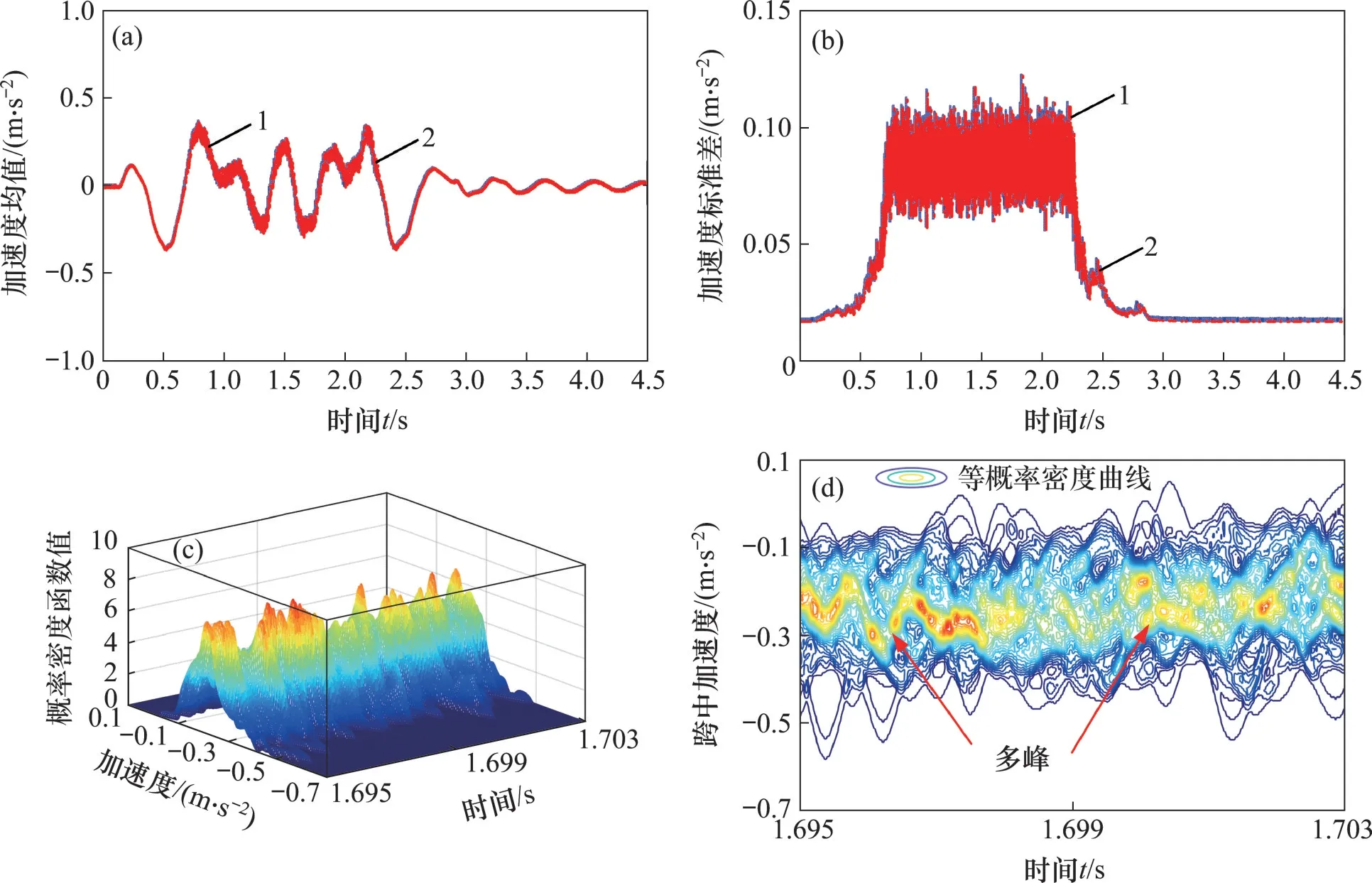
图6 轨道梁跨中加速度随机动力响应Fig.6 Random dynamic responses of guideway acceleration atmidpoint

4.2 车速影响分析

车速是影响系统随机响应的重要因素。将车速从100～500 km/h按50 km/h梯度增加，分别计算

9个工况列车以不同车速经过轨道梁过程中出现最大均值和标准差时的轨道梁跨中挠度和加速度、首车车体竖向加速度和悬浮间隙。相较于传统的取1 条轨道不平顺样本激励并取响应最大值方法，本文采用3σ 法则确定具有不同概率保证率的随机响应上下限。表3所示为不同车速下车桥系统随机响应。

从表3可以看出：系统响应随着车速增加基本增加；车速增加5倍，轨道梁跨中挠度和加速度均值分别增大0.13 倍和11.16 倍，车辆加速度和悬浮间隙均值分别增大9.25 倍和0.07 倍。轨道梁挠度和悬浮间隙受车速影响较小，而车辆和轨道梁加速度受车速影响较大。系统随机响应并非随车速的增加而线性递增，这与轨道梁和车体的多阶自振频率以及轨道随机不平顺激励有关。与传统的选取若干条轨道不平顺样本计算响应，然后从中挑选最大值的分析方法相比，采用基于概率思想的随机分析方法能得到具有概率保证率的响应分布范围，有利于揭示随机动力概率域分布特征。

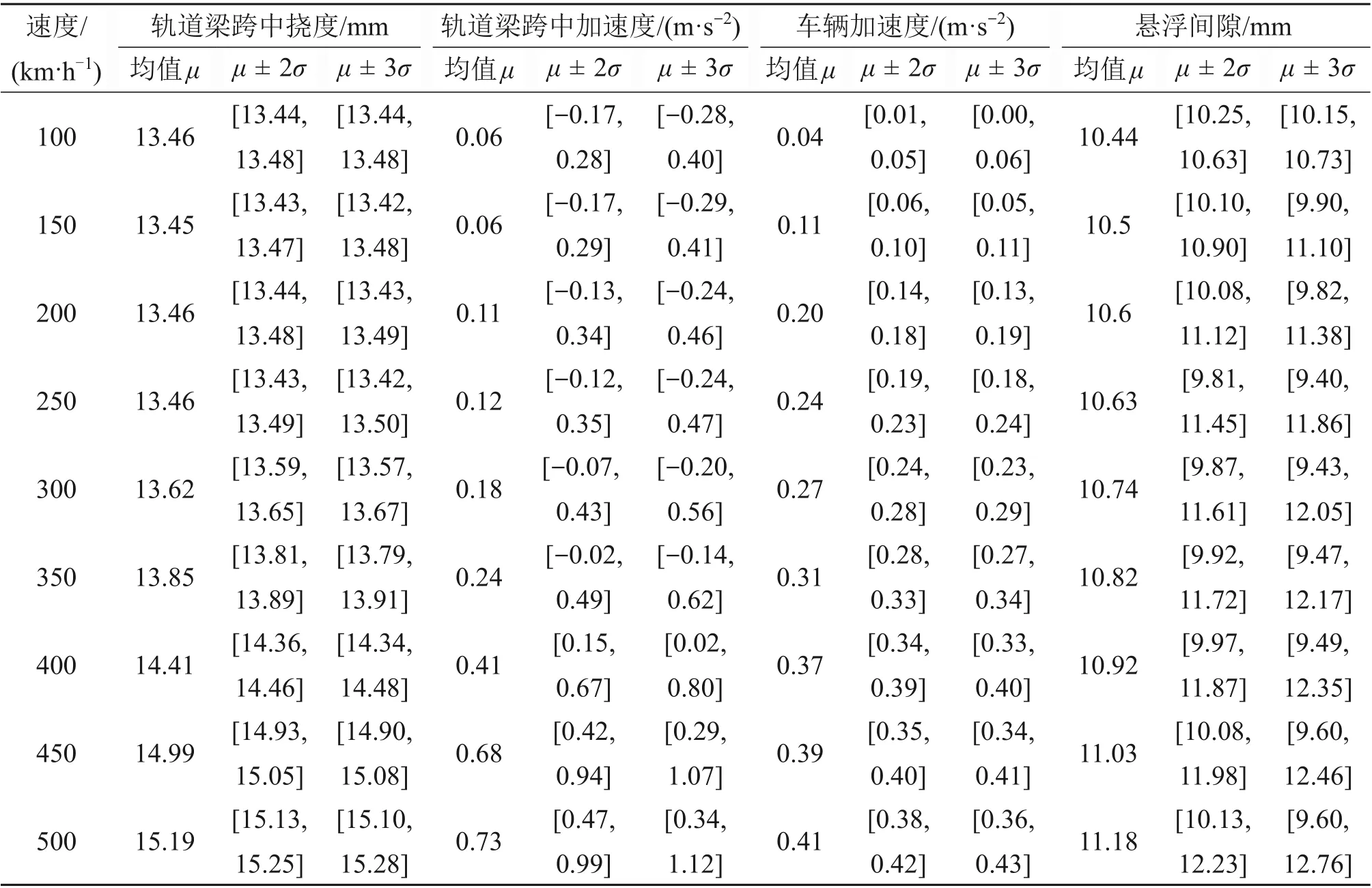
表3 车速对磁浮系统随机动力响应的影响Tab.3 Effect of vehicle running speed on random dynamic responses of maglev system

根据TB10630—2019“磁浮铁路技术标准(试行)”[22]规定，轨道梁最大加速度限值为0.350g，车辆最大加速度限值为0.125g。当概率保证率为99.7%时，轨道梁加速度最大值ag-max=1.12 m/s2，低于规范限值(3.50 m/s2)；车辆最大竖向加速度av-max=0.43 m/s2；低于规范限值(1.25 m/s2)。

不同车速轨道梁跨中挠度满足不同保证率的上、下限值非常接近，随机性变化很小。经进一步计算可知，确定性的车辆荷载起主导作用，这也与预期结果一致。轨道梁挠度最大值Dg-max=15.28 mm。

在不同车速等级下，悬浮间隙随机响应落在(μ± 3σ)区间内的概率保证率大于(μ± 2σ)区间的概率保证率。悬浮间隙的最大波动值约为2.76 mm。

4.3 支座刚度影响分析

支座是连接轨道梁和桥墩的传力装置，为避免出现过大的车辆和轨道梁振动，通常需要控制轨道梁支座安装刚度。保持车桥系统其他参数与轨道不平顺的相同，仅考虑支座刚度变化的影响以减少其他因素干扰，支座刚度在1.8×109～1.8×1012N/m之间变化，计算概率保证率为99.7%时车辆和轨道梁的响应均值、标准差和变异系数。图7所示为系统随机响应均值和变异系数随支座刚度的变化。

从图7 可以看出：当支座刚度从1.8×109N/m增加到1.8×1012N/m时，轨道梁动挠度、车体和磁转向架垂向位移的响应均值分别减小9.42%，7.92%和9.27%；当支座刚度大于1.8×1011N/m 时，各项指标均值基本保持稳定且变化幅度在0.5%以内；当采用较柔支座刚度时(1.8×109N/m)，轨道梁动挠度、车体和磁转向架垂向位移响应都增大；各项指标的变异系数均随支座刚度增大而递增，其中，转向架位移变异系数增大幅度为11.76%；达到稳定后，各项变异系数低于0.22%。

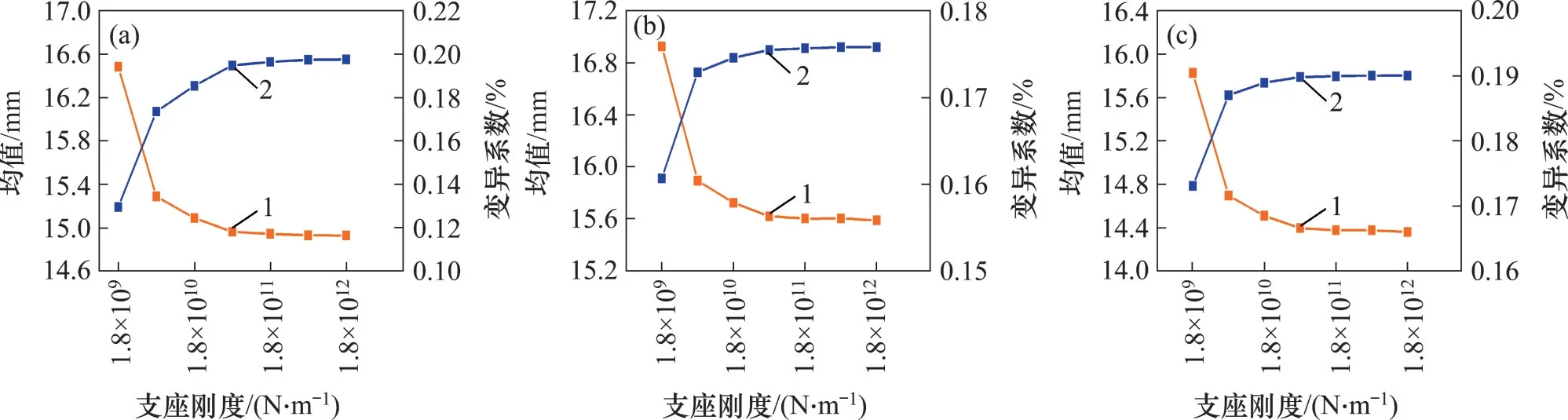
图7 支座刚度对动力响应的影响Fig.7 Effect of bearing stiffness on random dynamic responses

5 结论

1)建立的基于概率密度演化理论的磁浮列车-控制器-轨道梁时变随机振动分析方法具有较高的计算效率，与Monte Carlo 法相比，计算效率提高1～2个数量级。

2)在相同随机轨道不平顺激励下，轨道梁跨中加速度、首车车体加速度、轨道梁跨中挠度的变异系数分别为35.13%，2.25%和0.21%，轨道梁跨中加速度、首车车体加速度和轨道梁跨中挠度等概率密度曲线规则程度依次增大。

3)在概率保证率为99.7%时，轨道梁动挠度、车体和磁转向架垂向位移响应均值随着支座刚度增加而减小，采用较柔支座刚度将放大系统的动力响应。

4)随着车速增加，车桥系统响应均有不同程度增加，但并非呈线性成倍增加。