屏蔽气体流速对同轴双管式氦气大气压等离子体射流粒子分布的影响*

陈忠琪 钟安 戴栋† 宁文军

1)(华南理工大学电力学院,广州 510641)

2)(四川大学电气工程学院,成都 610065)

在大气压等离子体射流应用中,环境气体对射流流出物的影响不可忽视,尤其是在某些对环境粒子高度敏感的特定场景中.同轴双管式射流装置可用于抑制射流流出物与环境气体之间的相互扩散,从而控制射流流出物的化学性质.本文对同轴双管式氦气大气压等离子体射流在不同屏蔽气体流速下的放电特性和化学性质进行了数值仿真研究,并通过实验光学图像对仿真模型加以验证.结果表明,相比于没有屏蔽气体的情况,在高流速条件下放电得到增强,而在低流速下放电较弱;随着流速的增加,空间中的粒子数均随之增加,这可以归因于由屏蔽气体流速增加而产生的更宽的主放电通道.此外,不同浓度轮廓线上的离子径向通量受到流速的影响也存在很大差异.本研究进一步揭示了不同的放电位置对氮氧粒子产生的影响,加深了关于屏蔽气体流速影响等离子体射流放电行为的认识,并可能为等离子体射流的进一步应用开辟新的机会.

1 引言

大气压等离子体在生物医学、材料处理和环境应用等领域中受到了广泛关注[1-10].大气压等离子体射流(atmospheric pressure plasma jet,APPJ)也因其便捷性、无需真空腔体等优点而备受欢迎[11-17].APPJ 的常见配置是由工作气体(working gas,WG)流经介质管,等离子体在介质管中维持并从管嘴向外延伸一定的距离(厘米级).在此过程中,包含电离态、自由基态和激发态粒子的等离子体羽流与周围空气混合.这种混合效应会导致许多复杂的化学反应,产生大量的活性物质.然而,在不同的环境空气条件下,等离子体处理物品的性能不同且不可控制[18].为了在完全不同的背景条件下控制活性物质的输出,研究人员做了大量的尝试性工作.一种很有发展前景的方法是使用同轴双管式的反应器结构产生气幕以保护工作气体免受周围环境气体的影响[19,20].这种气幕常被称为屏蔽气体(shielding gas,SG)或保护气体,它不仅可以有效地抑制环境空气对等离子体羽的影响,还可以通过改变SG 的种类、流速等参数以控制射流流出物的成分[21].

在过去十几年中,研究人员对同轴双管式APPJ装置进行了一些实验和数值仿真研究以探索SG对射流的影响.如,Winter等[22]在实验中使用含有不同N2/O2比率的混合气体作为SG,结果表明,当SG 为空气(80% N2-20% O2)时,激发态粒子He(23S1)的密度达到最大值.Nguyen等[23]发现,由于SG 的引入,两个电介质管之间的次级放电明显减弱,射流长度、射流温度和放电功率/效率也会受到SG 种类的影响.

尽管之前的研究中对同轴双管式APPJ 的传播特性和放电行为进行了一些探索,但SG 化学成分对WG 及射流流出物的影响却很少被提及,放电空间中粒子的演化也尚未得到细致的描述.利用SG 对射流进行更精确的控制,需要进一步的实验和数值仿真手段以探索同轴双管式APPJ 流出物的性质.

APPJ 在管外空间中持续放电与空间中的稀有气体浓度有着密不可分的联系,在传播过程中,当空气分子与氦原子的比值超过一定值时,等离子体子弹的传播就会受到抑制[24,25].前人的研究表明,APPJ 中的电离波会大致沿着98%氦气浓度的轮廓线向前传播[26].而在同轴双管式APPJ 中,气体浓度分布会因SG 的引入而发生变化,这可能会使得APPJ 的放电范围受到影响.因此,从稀有气体浓度的角度来研究SG 对APPJ 的影响对进一步理解射流放电具有重要意义.

本文将主要通过数值仿真研究屏蔽气体(SG)流速对同轴双管反应器氦气大气压等离子体射流(APPJ)的放电行为和粒子分布的影响,并利用实验放电光学图像与模型中主放电通道宽度随SG流速变化的趋势进行对比以验证模型有效性.本工作采用氦气作为WG,环境气体及SG 均为空气(79% N2-21% O2).在此基础上,比较和分析了不同流速下APPJ 在放电空间中的时空演化过程.此外,本文还对三种氦气浓度(98%,95%,90%)等值轮廓线表面的粒子变化情况进行分析和讨论,以阐明SG 对射流流出物化学的影响.进一步分析表明,不同浓度轮廓线对应的放电位置对氮氧粒子的生成有很大影响.这项工作加强了关于SG 影响等离子体射流放电行为的认识,并进一步定性分析了放电位置与重要粒子生成之间的关系,这对大气压等离子体射流的基础研究具有重要价值.同时,深入了解并掌握SG 对氮氧粒子生成的影响规律和机理,对进一步调控空间中的等离子体特性和参数有实际指导意义.

2 实验与模型描述

2.1 实验描述

采用的实验装置结构如图1 所示.此反应器由两个呈同轴放置的介质管组成,高压针状电极位于反应器对称轴上,接地电极是由围绕在外侧介电管外表面的环形电极构成.内侧管的内径和外径分别为4和6 mm,外侧管的内径和外径分别为8 mm和10 mm.为了更好地通入气体,外侧管比内侧管高5 mm.反应器的其他几何参数如图2 所示.内侧管通入的WG是纯度为99.999%的氦气,其流速为3 slm (standard liters per minute,slm);通入内侧管与外侧管之间的环形空间的SG是空气,其流速变化范围是0—3 slm.针电极接入频率和峰值分别为5 kHz和4 kV 的正弦交流电压.放电光学图像由佳能EOS 6D 单反数码相机拍摄,曝光时间为1/8 s.

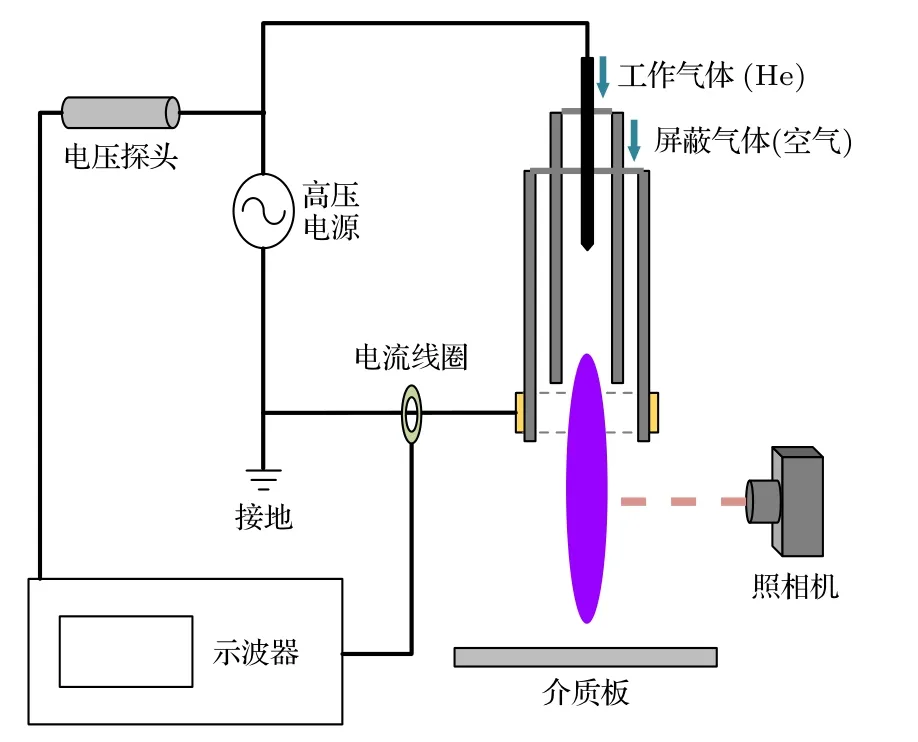
图1 实验装置示意图Fig.1.Schematic diagram of experimental setup.

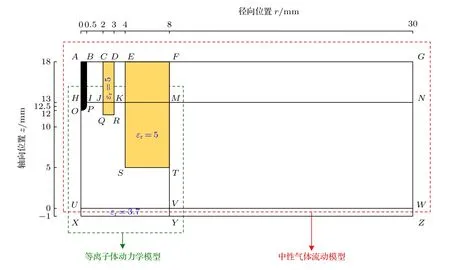
图2 仿真模型的几何结构Fig.2.The geometry of the simulation model.

2.2 仿真模型描述

采用的流体仿真模型由两部分组成: 中性气体流动模型和等离子体动力学模型.与其他文章中的建模方法一致,中性气体流动模型的结果用作等离子体动力学模型的初始值[27-29].这种方法被广泛应用是因为中性气体流动的特征时间尺度(ms)与等离子体动力学的特征时间尺度(ns)之间存在差异,即放电过程几乎不会影响到气体浓度在空间中的分布.WG(He)以3 slm 的流速流过内侧管,相应的平均流速为2.65 m/s (1 atm,300 K).SG(空气)以0—3 slm (平均流速为0—2.28 m/s)的流速通过两条介质管之间的环形通道.

2.2.1 模型的几何结构

图2 中的AUWGA 区域用于计算中性气体流动模型,而图中的HXYMH 区域用于计算等离子体动力学模型.这样的计算域配置方式是一种折衷方案,这样能够以较为合理的计算负担来模拟现实情况[30].与实验中采用的结构相比,仿真模型中的高压电极与接地电极的位置有所不同,高压电极放置在更加靠近管口的位置有利于降低混合气体的击穿电压,接地电极由附着在外侧介质管外表面改为计算域远端(XY和MY)接地,采用这样的接地方式可以使得模型得以简化且不会对仿真结果产生较大影响.此外,仿真模型中外侧介质管的外径也比实验中要大,这是因为更宽的介质管在不会对模型结果造成巨大影响的前提下能够使模型收敛性更好[31].

等离子体射流的特征时间尺度通常为纳秒级,相比于千赫兹级正弦电压下等离子体射流仿真的高计算成本[27],使用纳秒脉冲电压驱动一方面能够减少仿真的计算成本[28],另一方面也能反映出射流中更多的细节信息.因此,本文的仿真模型采用了一个幅值为4 kV、上升时间为50 ns 的正极性脉冲电压源,将其施加于尖端半径为0.5 mm 的半球形针状电极.此外需要补充说明的是,根据Kettlitz 的研究[32],由千赫兹级正弦电压驱动的放电行为和由脉冲电压驱动的放电行为在时空结构上没有很大差异,本文受实验条件限制,在实验研究中使用了千赫兹级正弦电压源.

2.2.2 中性气体流动模型的控制方程和边界条件

在中性气体流动模型中,通常使用Navier-Stokes 方程(1)、连续性方程(2)和对流扩散方程(3)来计算空间中的气体流动情况:

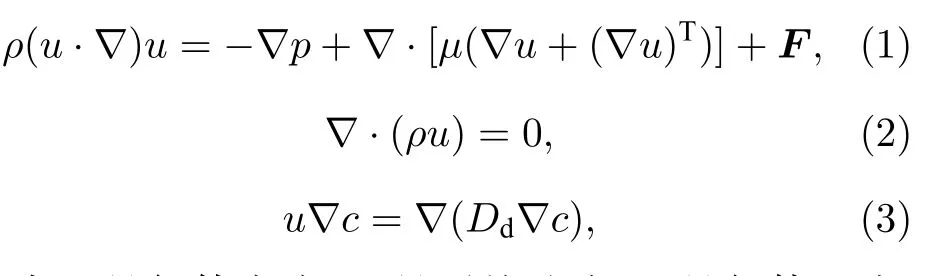
其中ρ是气体密度;u是平均速度;p是气体压力;µ是气体动力黏度(氦气: 1.94× 10—5Pa·s,空气:1.82× 10—5Pa·s);F是体积力矢量,Dd是氦气和空气之间的扩散系数(7.2× 10—5m2/s);c表示氦气的摩尔分数(单位: mol·m—3)[27].

中性气体流动模型的边界条件如表1 所列.

表1 中性气体流动模型的边界条件Table 1.Boundary conditions of the neutral gas flow model.

2.2.3 等离子体动力学模型的控制方程和边界条件

在等离子体动力学模型中,电子数密度ne和电子能量密度nε通过漂移—扩散近似求解连续性方程得出[33,34]:

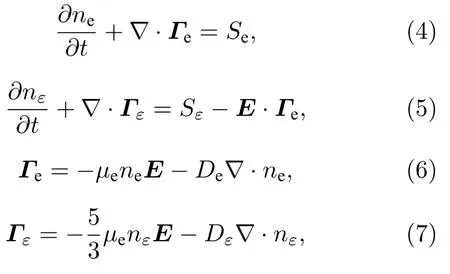
式中,Γe,µe,De和Se分别代表电子的通量矢量、迁移率、扩散系数和源项;De是由爱因斯坦关系(De=µekBTe)推导而来,其中kB是玻尔兹曼常数,电子温度Te是平均电子能量;电子能量密度nε由nε·ne 得到;E是电场;Γε,Dε和Sε分别表示电子能量的通量矢量、扩散系数和源项.

放电空间中的电场由泊松方程(8)确定,其中ε0和εr分别表示真空介电常数和相对介电常数(气体为1,介电管为5,下游介质板为3.7),V表示电势,ρv表示空间中的电荷密度.

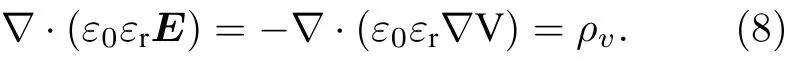
电子、离子、激发态粒子和电子能量密度在壁面上的法向通量可以用以下公式来描述[33,34]:

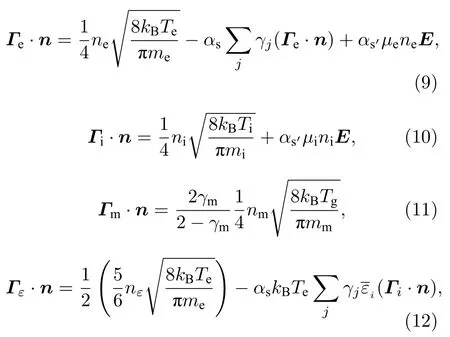
式中,向量n是单位法向量,其方向指向壁面;二次电子发射系数γj设为0.01;γm是激发态粒子与壁碰撞失活的概率(设为1);气体温度Tg=300 K;αs和αs′是开关函数,其值由E·n确定:

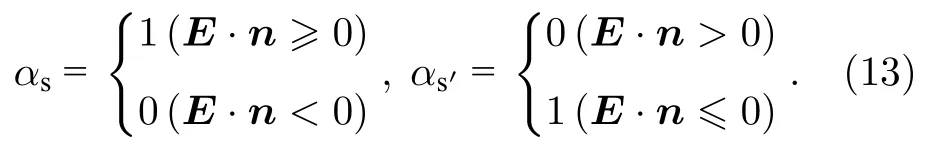
介质表面电荷积累的边界条件由下列式子确定:

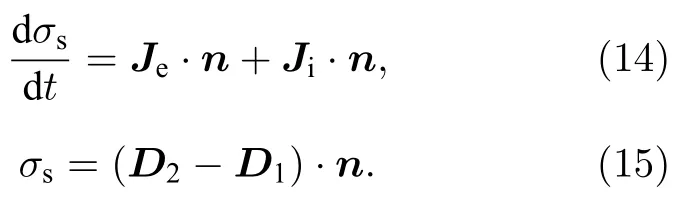
其中σs为表面电荷密度;Je和Ji分别为表面上电子电流密度和离子的电流密度;D1和D2分别表示介质层表面两侧的电位移矢量.

等离子体动力学模型的边界条件见表2.

表2 等离子体动力学模型的边界条件Table 2.Boundary conditions of the plasma dynamics model.

2.2.4 等离子体动力学模型中的化学反应

本工作中使用的化学反应体系与我们小组之前的文献中相类似.等离子体化学反应体系一共包含了16 种粒子,66 个化学反应,已在附录表A 中列出.此外,本模型中将初始电子密度设置为1014m—3以替代光电离过程[30].

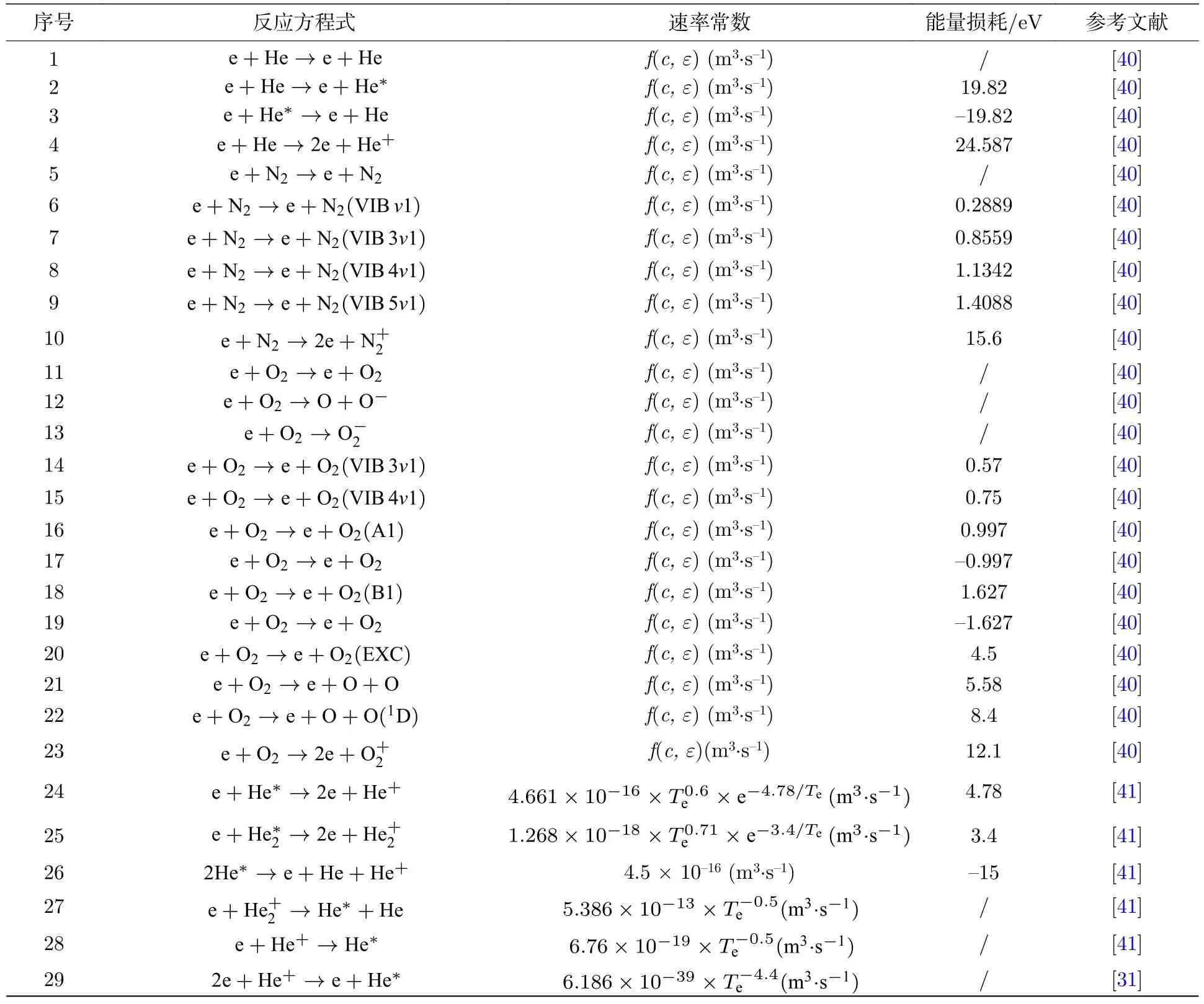
表A 等离子体化学反应Table A.Chemical reactions considered in the plasma dynamics model.

3 结果与分析

基于仿真手段及实验放电光学图像对照,3.1 节对两者的结果进行对照以验证模型有效性.基于此模型,3.2 节讨论了放电空间中粒子分布情况及其原因.为了度量SG 对环境气体扩散进入主放电区域参与化学反应的抑制效果,3.3 节将从三种稀有气体浓度(98%、95%和90%)轮廓线上离子通量变化的角度分析SG 对射流流出物化学性质的影响.

3.1 模型验证

当APPJ 被下游的介质板阻挡时,气流的运动状态很容易从层流模式转变为湍流模式.又因为在层流模式下,等离子体羽流的长度随流速或速度线性增加[35].因此,层流模式下的气流更适合等离子体子弹的传播.在此前提下,有必要通过雷诺数(Re)大小判断气流是处于层流模式还是湍流模式.雷诺数可以使用以下公式求得[36]

其中u,ρ,d和µ分别是气流的平均速度、密度、特征长度和流体流动的动力黏性系数.当WG和SG的流速均为3 slm 时,它们的雷诺数分别为91和729.根据[35,37],此时的WG和SG 均处于层流状态.实验结果(图3)的图像表明: 当SG 流速为1 slm 时,放电区域(红色曲线内部区域)略小于没有SG 的情况;当SG 流速处于3 slm 时,其放电区域明显大于没有SG 的情况.此外,当SG 流速为3 slm 时,没有明显的湍流现象,这可能是由于WG和SG 的平均流速较低[38].

图3 不同SG 流速下的放电光学图像 (a),(c)0 slm;(b)1 slm;(d)3 slm.红色曲线表示放电时最明亮的区域Fig.3.The discharge optical images for the different SG flow rates: (a),(c)0 slm;(b)1 slm;(d)3 slm.The red curve shows the brightest region of the discharge.

根据文献[26-28],等离子体子弹主要沿着氦气含量约为98%的等值线传播.图4 显示了不同SG流速下的中性气体流动模型结果中的氦气浓度分布,其中0 slm 表示外侧管中不通入屏蔽气体,0.5 slm表示SG 的流速为0.5 slm,以此类推.图4(b)示了氦气摩尔分数在轴向位置z=2.5 mm 处沿径向分布情况,图4(c)为图4(a)中指定区域的放大图.从图4(b)和图4(c)中可以看出,当SG 的流速为3 slm 时,cHe=98%的等值线范围最大,然后随着流速的降低而逐渐减小.特别地,不通入SG 情况下,氦气浓度cHe＞ 98%的区域还略大于0.5,1和1.5 slm 情况下的结果.这一现象表明,低流速的SG 会将更多的氦气带到远端,导致氦气摩尔分数cHe＞ 98%的区域比没有通入SG 的情况下的结果小.结合实验结果表明中性气体流动模型的仿真结果与实验结果是一致的,即在低流速下,中性气体流动模型中的主放电通道和实验中的放电区域不如没有SG 的情况;而在高流速下,中性气体流动模型结果和实验结果均优于无SG 的情况下的结果.

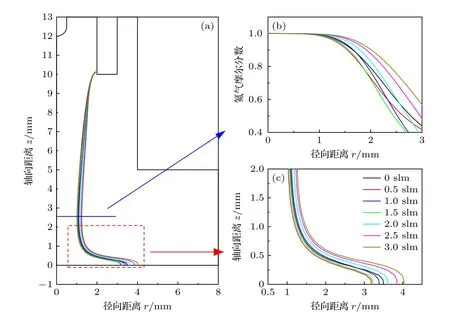
图4 (a),(c)不同SG 流速下98%氦气摩尔分数的轮廓线;(b)氦气摩尔分数(cHe)在轴向位置z=2.5 mm 处的径向分布Fig.4.(a),(c)The contour line of the 98% helium mole fraction at different flow rates of SG;(b)the distribution of the helium mole fraction(cHe)at axial position of z=2.5 mm.

当SG 处于不同流速时,各模型放电最后时刻(射流沿介质板表面径向放电到达98%轮廓线最大径向位置处所对应的时刻)的电子密度的时空分布见图5 所示.对比图中三条轮廓线,98%氦气浓度轮廓线更加靠近电子密度集中的区域.因此,在本文中,98%氦气摩尔分数(cHe=98%)的轮廓线表示主放电通道的边界[26].从图5 还可以看出,不同流速下的SG 不会显著改变等离子体羽流的形态.特别地,随着SG 流速的增加,主放电通道逐渐变宽.当SG 处于低流速时,主放电柱比没有SG时窄.由此可以看出等离子体动力学模型的结果与中性气体流动模型以及实验现象中所描述的结果一致.因此,本研究中使用的模型是有效的[27].

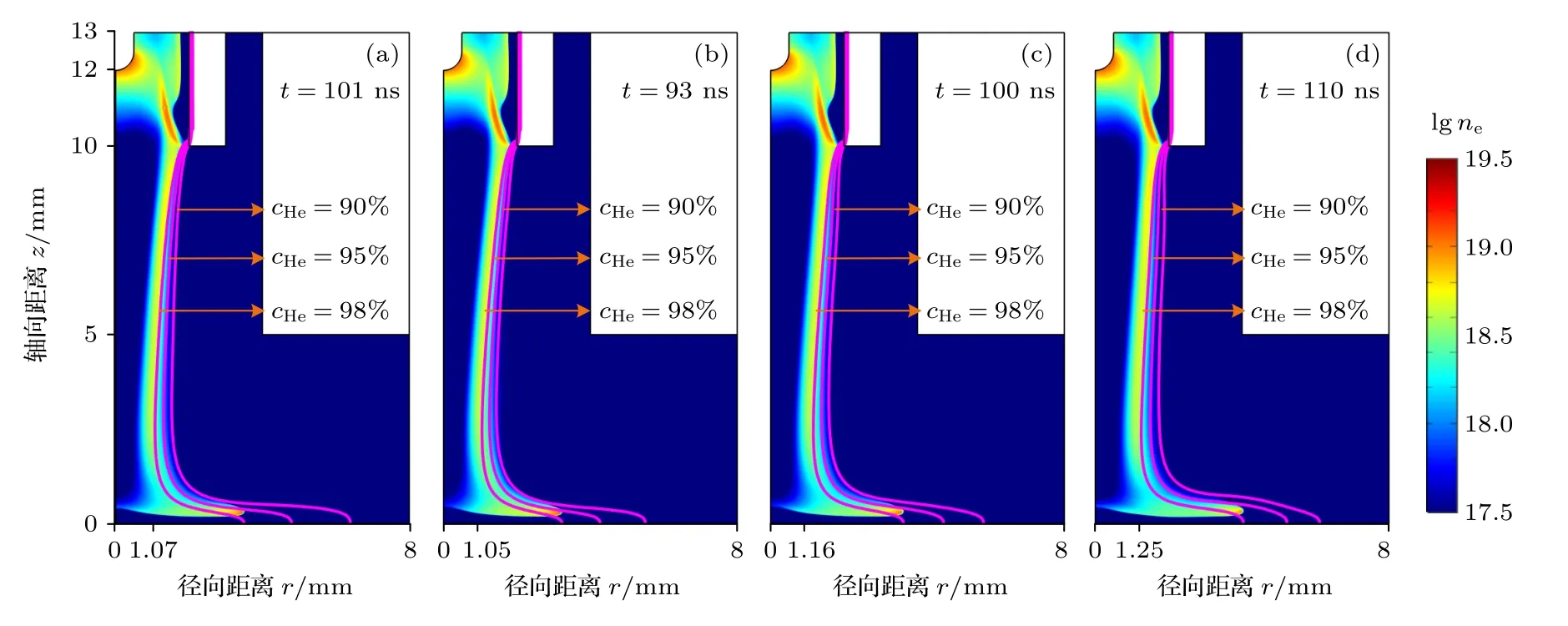
图5 当SG 流速处于(a)0,(b)1,(c)2和(d)3 slm 情况下,电子密度ne(单位: m—3,以对数形式表示)的时空分布.洋红色线分别表示不同氦气摩尔分数的等值轮廓线Fig.5.Spatial and temporal profiles of the electron density ne (unit: m—3,in 10 logarithmic scale)for SG flow rates of (a)0,(b)1,(c)2 and (d)3 slm.The magenta lines are the contour lines of different helium mole fractions.

3.2 放电空间中粒子分布情况

图6 描述了当SG 流速为0和3 slm 时,放电空间中电离率的时空演化过程.从图6 中可以看出,电离波几乎沿着这三条轮廓线向下游介质板发展,直到放电阶段结束.此外,还可以明显地看出,改变SG 的流速会影响主放电柱的宽度及其沿介质板表面放电的区域大小.

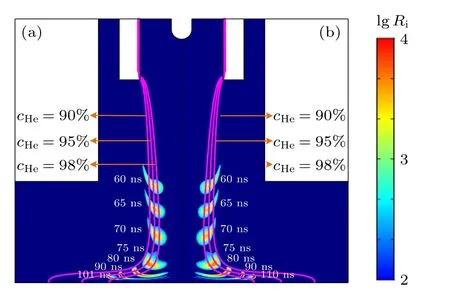
图6 SG 流速为(a)0和(b)3 slm 情况下放电空间中电离率(单位: mol·m—3·s—1,以对数形式表示)的时空演化情况.洋红色线分别表示不同氦气摩尔分数的等值轮廓线Fig.6.Development of the ionization rate (unit: mol·m—3·s—1,in 10 logarithmic scale)in the discharge region for SG flow rate of (a)0 and (b)3 slm.The magenta lines are the contour lines of different helium mole fractions.

图7(a)所示是放电空间中的粒子平均数密度随SG 流速变化的对比结果.由此可知,当介质管中通入SG 后,随着SG 流速增加,主放电通道逐渐加宽,放电空间中粒子平均数密度均随之增加.值得注意的是,未通入SG 情况下的空间平均粒子数密度与SG 流速为1.5 或2 slm 情况下的结果接近.即当通入的SG 流速较低时,由于SG 的屏蔽效果不好,间接导致放电空间中粒子数密度有所下降;而当其流速大于2 slm 时,SG 的屏蔽作用显著,因此放电空间中粒子数密度明显增加.

此外,在放电空间中整个放电阶段的各粒子平均生成速率如图7(b)所示,粒子的产率与SG 流速也呈现出正相关的关系,也和放电空间中平均粒子数密度随流速变化的趋势一致.从图7(b)可以看出,在主放电通道内,He*粒子反应速率没有较大差异,主要的区别还是在于该粒子参与反应的空间位置,即主放电通道边界的位置.换而言之,SG流速变化几乎不会影响APPJ 主放电通道内粒子产率,只是由于SG 流速影响主放电通道大小从而导致空间中粒子数增多或减少.

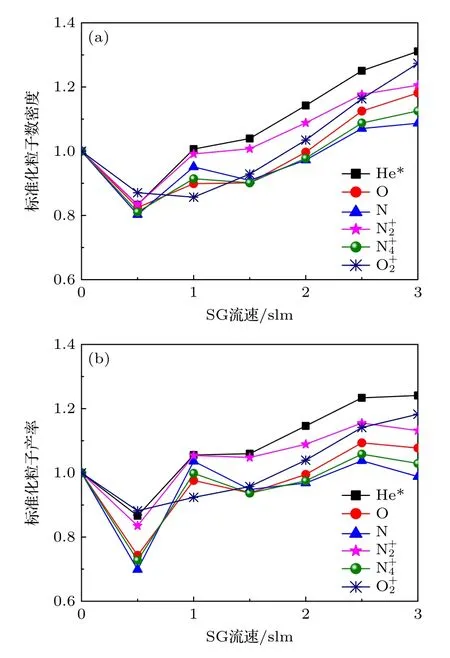
图7 放电空间中(a)粒子平均数密度及(b)各粒子时间空间平均生成速率Fig.7.(a)The average species density and (b)the average spatiotemporal production rate of the species in discharge region.

3.3 放电空间中粒子通量变化情况

由上文分析可以得出,SG 流速几乎不影响粒子的产量,但会影响主放电通道的区域大小.当外侧管通入屏蔽气体时,放电柱(或主放电通道)随着流速的增加而逐渐变宽.为了探究主放电通道的宽度变化如何影响从环境气体(空气)到主放电通道内的粒子通量,下面分析了主放电通道表面及其他氦气浓度轮廓线表面的离子径向通量.本文选取的轮廓线表面并非是整条轮廓线表面,而是取各条轮廓线其中一小段,并对这一小段轮廓线进行分析(见图8).对于98%氦气浓度轮廓线,本文选取轴向位置z=10.54—10.56 mm,对于95%和90%氦气浓度轮廓线,本文选取的位置分别为z=10.14—10.16 mm和z=10.34—10.36 mm.

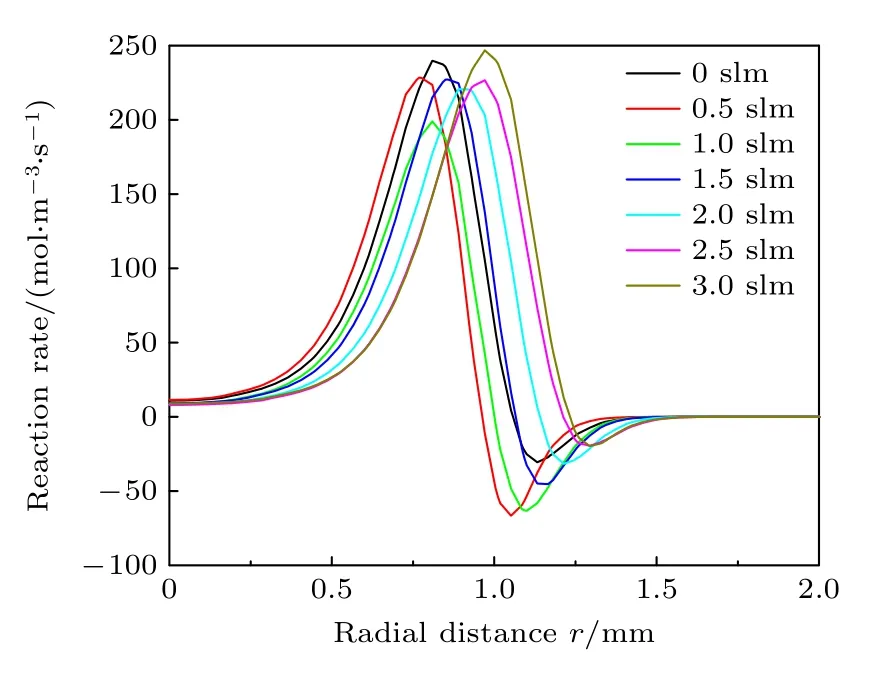
图8 轴向位置z=2.5 mm,He*粒子的生成速率沿径向分布Fig.8.Radial distribution of the production rate of He* at axial position z=2.5 mm.

此外,部分研究小组将95% He和90% He 浓度轮廓线近似当作主放电通道的边界[30,39],本文将对这三种氦气浓度轮廓线进行区分和比较.由图9(a)可以看出98% He 浓度轮廓线表面O—,和的通量随着流速增加而逐渐增加,而的通量几乎不受SG 流速或主放电通道宽度的影响.

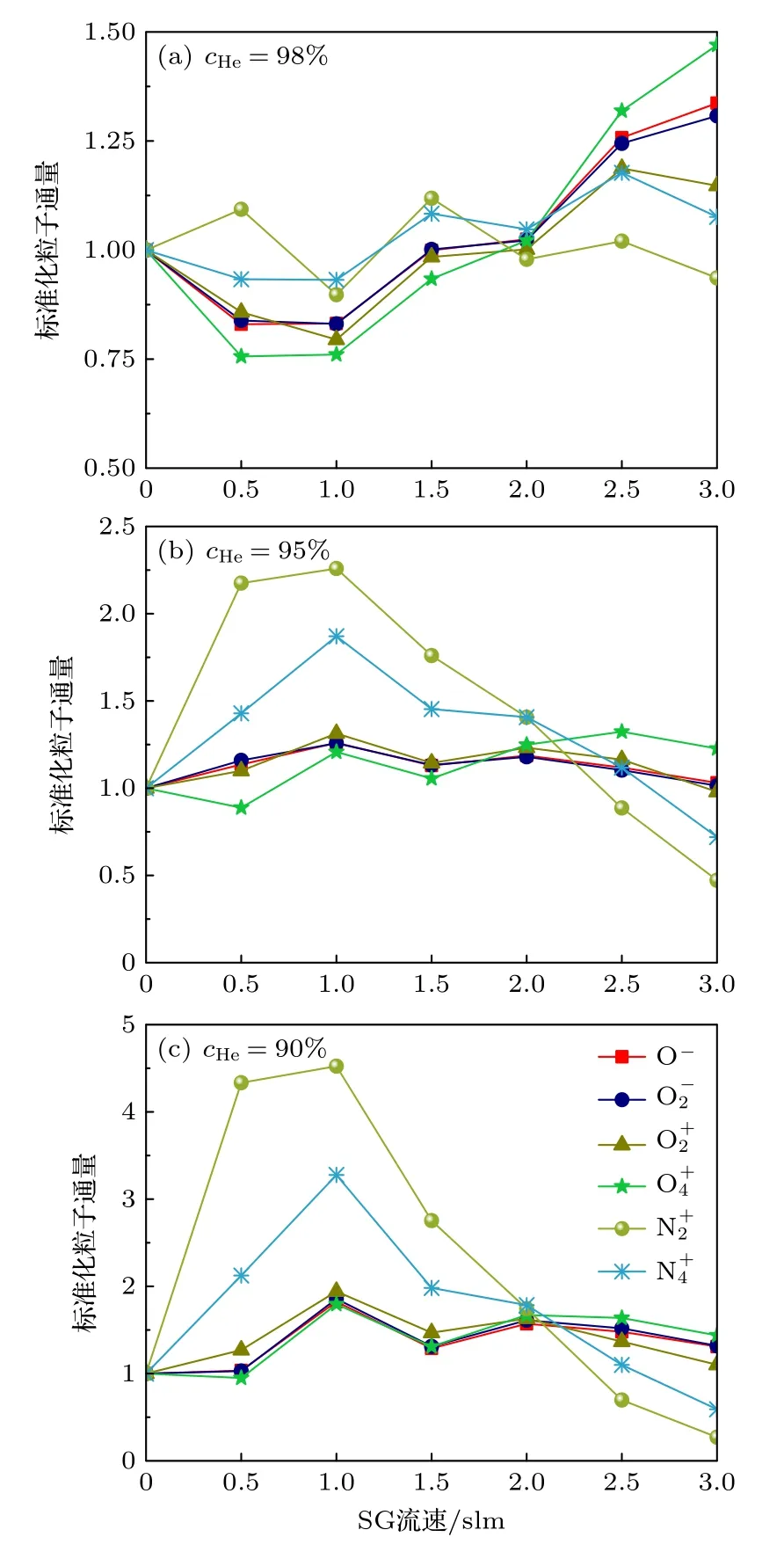
图9 不同氦气浓度轮廓线表面的离子径向通量Fig.9.Radial flux of ions on the contour lines of different helium mole fractions.

空间中离子的通量可由下式求得

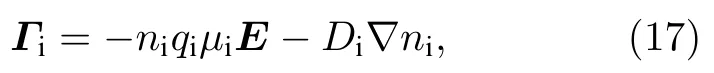
式中,ni表示离子数密度;qi,µi,Di分别表示离子的电荷数、混合物迁移率和扩散系数.

从方程(17)可以看出,离子通量Γi与电场E和离子数密度ni正相关.然而,离子数密度ni是会受时空累积效应影响的状态量,所以本文只考虑离子的生成速率(即化学反应速率)和电场的变化.从图10和图11 可以看出,和是放电柱中主要的离子.因此,本文后续将对这些离子的通量变化进行分析.

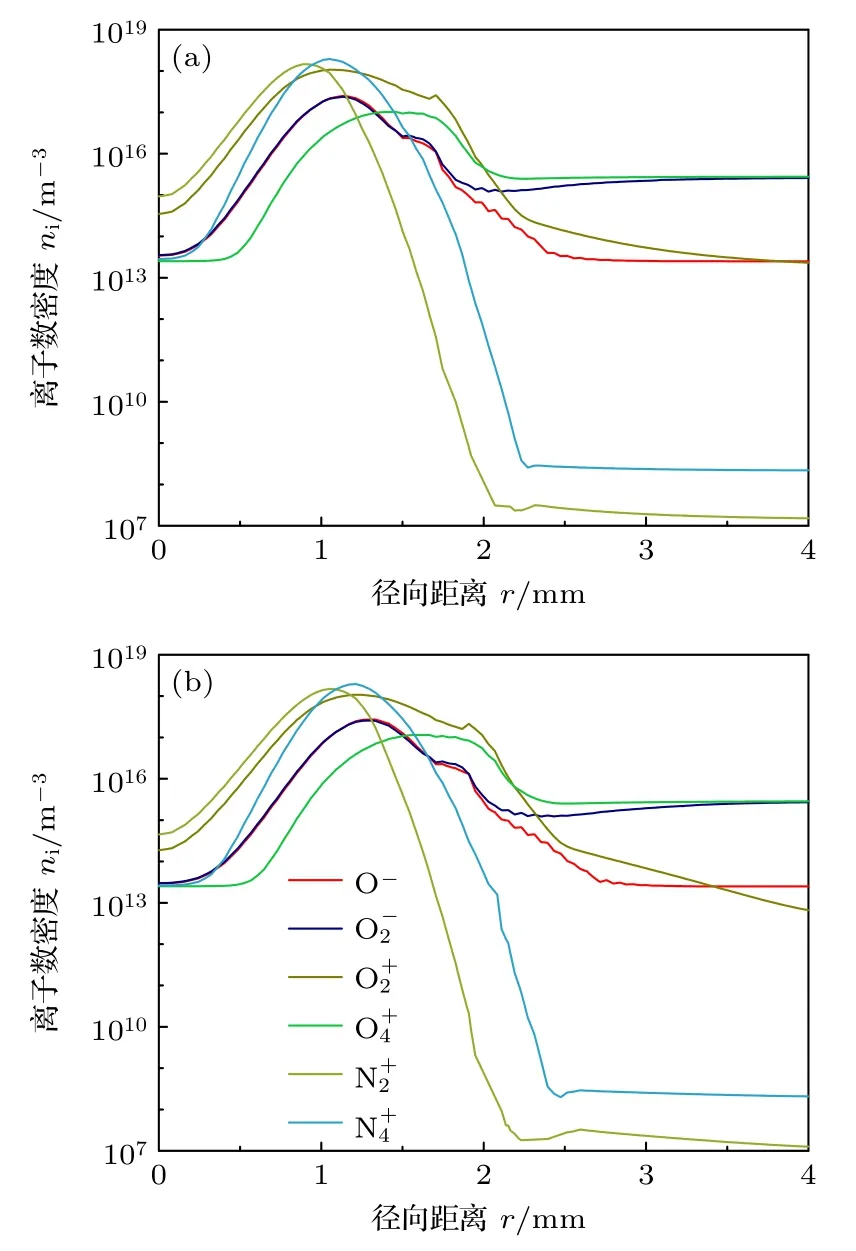
图11 当SG 流速为(a)0和(b)3 slm 时,轴向位置z=2.5 mm 处的离子密度沿径向位置分布Fig.11.Distribution of ion density at axial position z=2.5 mm for SG flow rate of (a)0 and (b)3 slm.

表3 所列为氦气浓度为98%,95%,90%的轮廓线表面与和相关的化学反应速率.值得注意的是,表3是对各自轮廓线中选定的一小段上化学反应速率进行线积分后的结果.由此可以看出,离子以消耗反应(R46,R58,R63)为主,这些反应的主要生成物是离子;而此处的也是以消耗反应(R64)为主,主要生成物是离子;以消耗反应(R51)为主,主要产物是.

表3 与和相关的化学反应速率Table3.Reaction rates involvingand.

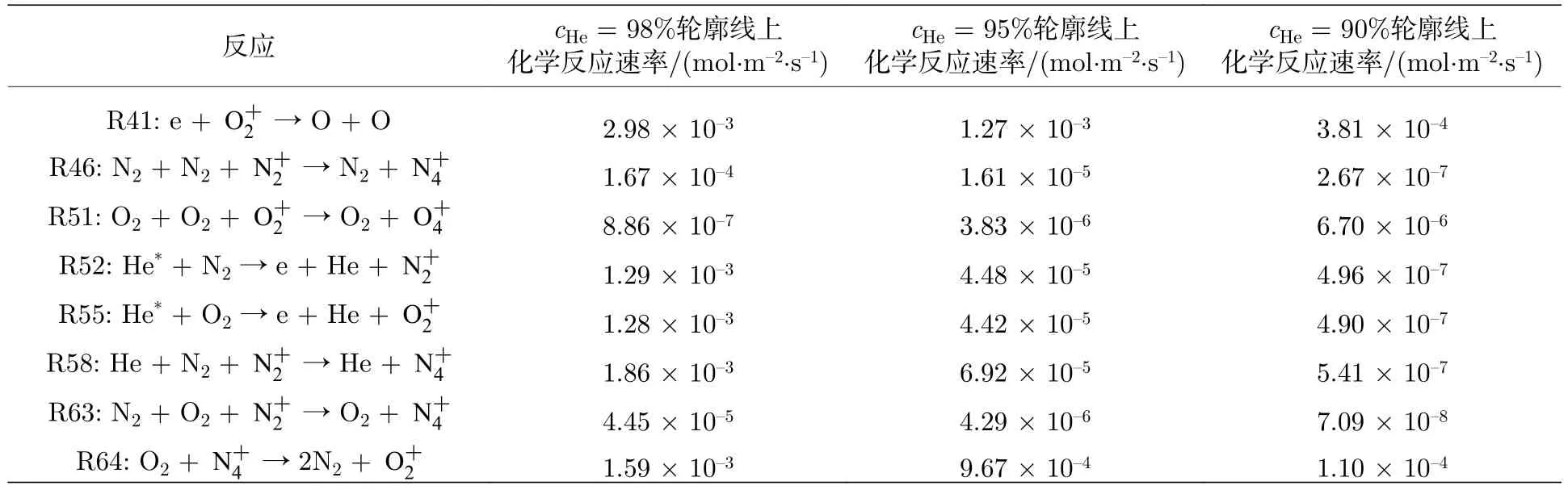
表3 与和相关的化学反应速率Table3.Reaction rates involvingand.

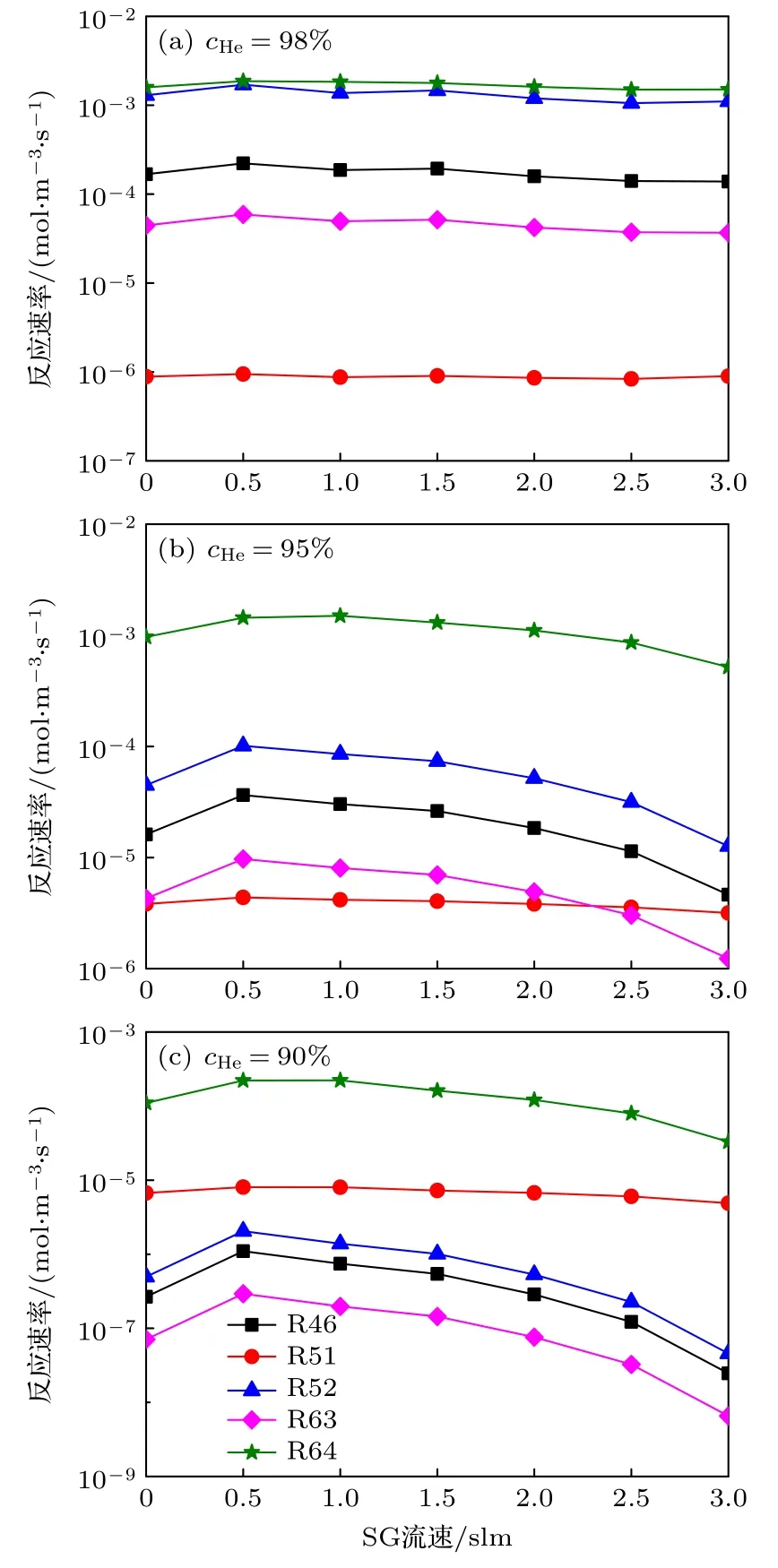
图10 不同氦气浓度轮廓线表面的化学反应速率Fig.10.Reaction rate on the contour lines of different helium mole fractions.

当SG流速 为3 slm且t=110 ns 时,和生成速率的空间分布如图13 所示.结果表明,与有关的化学反应主要发生在主放电通道表面外围,而与和有关的化学反应主要发生在靠近对称轴的地方.这是因为N2的电离能(15.6 eV)高于O2的电离能(12.6 eV),意味着O2发生电离的可能性更大.此外,电子能量在主放电通道内部分布均匀,随着径向距离的增加,电子能量在主放电通道外部逐渐减小[31],因此与相关的化学反应的空间分布比更为广泛.值得说明的是,(R54,R55)的彭宁电离反应速率为6.2× 10—16mol·m—3·s—1,远高于N2(R52,R53)的1.4× 10—16mol·m—3·s—1.由于98%He 浓度轮廓线较为靠近主放电通道,与有关的化学反应受到的影响较小,而与有关的化学反应受到的影响较大.又由于轮廓线上的电场与屏蔽气体流速有着正相关的关系,所以等离子的通量随着流速增加而逐渐增加,而,离子通量几乎不变.

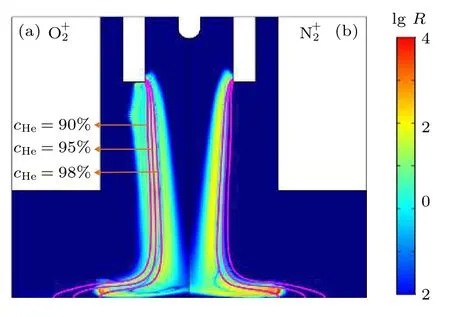
图13 和的化学反应速率的空间分布.洋红色线分别表示不同氦气摩尔分数的等值轮廓线Fig.13.Spatial distribution of the reaction rates involving(a) and (b) .The magenta lines are the contour lines of different helium mole fractions.

此外,95% He和90% He 浓度轮廓线表面粒子通量变化情况如图9(b)和图9(c)所示.在图9(b)和图9(c)中,这两条轮廓线表面的,离子通量随着流速增加而逐渐降低,其中离子的通量变化甚至高达70 倍.相比于和离子,O—,和的变化只有2 倍.因此,可以认为O—,和几乎不受SG 流速或主放电通道宽度的影响.而图12 结果表明,流速的变化并不会导致这两条轮廓线上的电场发生较大变化.从图10(b)和图10(c)可以看出,粒子相关的反应的速率与屏蔽气体流速也有着负相关的关系,而粒子相关的反应的速率则几乎不受其影响.这也导致了和粒子通量的变化规律有着如此大的差异.

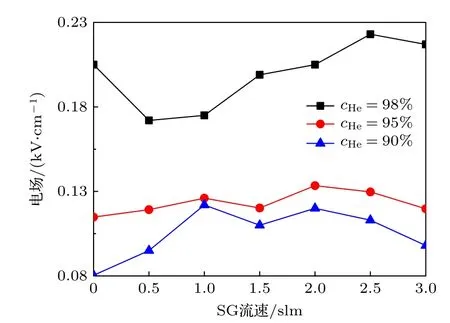
图12 不同氦气浓度轮廓线表面的径向电场变化情况Fig.12.Variation of the radial electric field on the contour lines of different helium mole fractions.

由于95%和90% He 浓度轮廓线更靠近主放电通道外围,与有关的化学反应受到的影响较小,而与有关的化学反应受到的影响较大;同时,由于两条轮廓线上的电场变化不大,所以等离子的通量几乎不变,,离子通量随着流速增加而逐渐降低.

4 结论

本研究通过仿真研究了屏蔽气体(SG)流速对氦气大气压等离子体射流(APPJ)的放电行为和粒子分布的影响,利用实验中放电光学图像与模型中主放电通道宽度随SG 流速变化的趋势进行对比以验证模型有效性.结果表明,当少量屏蔽气体被引入外侧管时,SG 的屏蔽效果不好,更多的稀有气体氦气溢出,放电强度减弱;当SG 流速高于2 slm 时,SG 的屏蔽效果明显,放电得到增强.

在此基础上,研究了SG 流速对放电空间中粒子数密度的影响.仿真结果表明,当外侧管通入SG 时,放电空间中的粒子数密度与SG 流速呈正相关,这可以归因于较高的SG 流速导致更宽的主放电通道.

本文还讨论了不同浓度轮廓线表面的径向离子通量以探究SG 对射流流出物化学的影响.研究发现,主放电通道(98%氦浓度等值线)表面的和的通量几乎不随流速变化,而O—,,和的通量随SG 流速的增加而增加.而在95%和90% He 浓度等值线表面,O—,,和的通量几乎不受SG 流速的影响,并且和的通量随着SG 流速的增加而减少.这是因为: 一方面,这些轮廓线表面的粒子生成率和径向电场受到SG 流速不同程度的影响;另一方面,与和等离子的化学反应主要发生在主放电通道外围,而和的反应主要发生在靠近主放电通道的位置.

此项研究有助于进一步理解屏蔽气体对射流的影响,这对大气压等离子体射流的基础研究和实际应用具有重要意义.

附录

表A（续）等离子体化学反应Table A (continued).Chemical reactions considered in the plasma dynamics model.