基于图卷积STG-LSTM的京杭运河水质时空预测研究

2022-08-28徐宪根杨贝尔蒋建明

中国农村水利水电 2022年8期

宦娟，张浩，徐宪根，杨贝尔，史兵，蒋建明

（1.常州大学计算机与人工智能学院阿里云大数据学院，江苏常州 213164；2.常州市环境科学研究院，江苏常州 213022）

0 引言

为了更好管理流域水质状况，我国部分河流已建立较为完善的监测体系。溶解氧含量对调节河流生态系统中的各种化学过程和生物群落中起着关键的作用，氮磷是自然河流及湖泊中影响水体营养状态及浮游植物生产力的最主要营养因素［1］。但河流水质具有时序性、不稳定性和非线性等特点且受多种因素影响，会产生时间和空间上的分布差异。因此，提高河流水质因子时空预测的准确度，有利于对河流不同位置的水质状态进行快速预警和精准调控。

河流水质的时空预测是以河流水质状态信息作为研究对象，根据其时空分布特征，利用水质历史数据对未来一段时间的水质时空状态做出预测。在早期的预测方法中，学者们提出马尔科夫模型［2］、自回归移动平均模型（ARMA）以及其变种的自回归差分移动平均模型［3］（ARIMA）等统计学预测模型。这些统计学预测模型共同的特点是需要数据平稳性假设，由于提取河流水质因子的非线性特征能力不足，其预测的精度不高。支持向量机［4］（SVR）、高斯过程回归［5］（GPR）和极限学习机［6］（ELM）等机器学习方法能够对河流水质数据进行特征工程建模并能很好的提取非线性特征，从而能够提高预测精度。近年来，深度学习方法在提升预测精度方面取得了优异的性能，被广泛应用于各行各业［7］。Yu 等提出了小波分析和长短时记忆神经网络（LSTM）组合的方法用于预测湖泊叶绿素含量，利用小波分析去除采集到数据中的噪声，再利用LSTM 捕获数据长期时间依赖特征，取得了较好的预测效果［8］。CAO 等建立了基于门控结构（GRU）的溶解氧时间序列预测模型，将时间区间划分成不同的时间段，依次对不同时间段内水体溶解氧进行预测［9］。上述对于水质因子的预测方法都是针对单监测站点的时间序列预测，而河流水质因子数据不仅在时间上具有依赖性，在空间上河流不同位置上的水质状态也具有一定的空间关联性，所以仅从时间维度上考虑，无法获取河流不同位置上水质状态的变化，预测精度还有待进一步提高。樊星宇等通过RELM 构建出中心监测点与池塘各位置溶解氧之间的映射关系，从而实现对未来时刻池塘溶解氧的空间预测［10］。自从谱图理论将卷积运算从基于网格的数据推广到基于图结构数据上后，交通领域的研究者利用图卷积神经网络（GCN）提取交通流的空间特征，李志帅等依据路网中的传感器空间分布的非欧式结构特征，将其抽样成一张图，并使用GCN 提取图中的空间关联性［11］。Zhu等提出了一种基于门控图卷积网络地交通流预测方法［12］。由此可见，GCN 能有效的提取非欧式空间数据蕴含的空间特征。

依据上述问题和方法，本文提出一种融合河流水质状态时空特征的STG-LSTM 模型，通过构建出时空图，得到未来一段时间河流不同位置的水质状态。以此探究通过提取时空关联性后，模型所体现出优越性。首先，采用最大互信息系数（MIC）衡量各监测站点水质因子序列之间的相关性，综合选取时空预测站点；其次以各监测站点地理位置和水质因子历史观测值为依据，构建时空图来表征各监测站点间的时空相关性。将时空图输入STG-LSTM 模型中，采用图卷积获取河流水质因子空间依赖关系，并融合长短时记忆神经网络获取水质因子的时空关联性。通过选取时空预测站点将本模型与其六种模型进行比较，并依据所构建的时空图，实现对未来一段时间运河河段不同位置水质状态的时空预测。

1 材料与方法

1.1 研究区域与数据

本研究以京杭运河常州段作为试验区域，该河段分布多个国控和省控的水质断面监测站点。收集了2020年4月1日-2021年4月1日8个监测站点的4种水质因子数据，监测时间间隔为4 h，水质数据共17 168 组。该4 种水质因子分别为溶解氧、高锰酸盐指数、氨氮和pH值，这8个监测站点能够很好的掌握该运河河段上不同位置水质因子的变化情况。其中监测点D的4 种水质因子数据，见图1。每个监测点有2 146 组数据，将前1 546 组数据划分为训练集，后600组数据作为验证集。

图1 监测站点D四种水质因子数据曲线Fig.1 Data curve of four water quality factors at monitoring site D

1.2 时空预测站点的选取方法

由于运河河段各监测站点所在的位置和环境的不同，导致了各监测站点的水质序列之间存在相关性的差异。最大互信息系数（MIC）可以较好的衡量两个序列之间的相关性［13］。本文采用最大互信息系数来衡量河流上各个监测站点上水质因子之间的相关性，综合选取出与其他站点相关性最大的站点作为时空预测站点。

假设运河河段站点数量为N，以溶解氧序列为例，任意选取两个站点，将两个监测站点的溶解氧序列和的值域分别划分为x 段和y 段，以获得xy 个网格划分结果。则河流监测站点i和j溶解氧序列的最大互信息系数为：

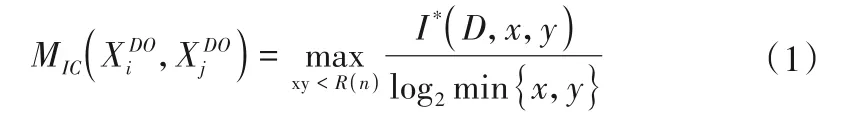
式中：D 为两个监测站点溶解氧序列；I*(D，x，y)为划分网格后每一个网格中相关互信息的最大值；Rn为网格划分数量xy的最大值。

最后计算第i监测站点与河流上其余监测站点溶解氧序列的最大互信息系数的和，选取最大的监测站点作为时空预测站点，计算公式如下：

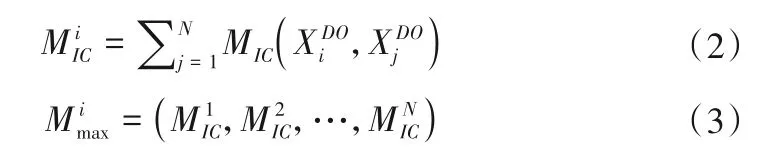
1.3 运河各监测站点时空图的构建

在某一时刻，运河河段上的各个监测站点空间分布可以被抽样成一个空间拓扑图，记为W =(V，E，A)。其中V ∈RNF表示构成图结点的集合，N 为运河监测站点的个数，F 表示每一个监测站点的属性维度。E ∈RNN表示构成图的边集合，代表各监测站点之间的连通性；A ∈RNN表示图G 中的空间关系邻接矩阵，其中每一个元素Ai，j表征图节点vi和vj之间的相对时空关系。

在对运河河段水质因子预测的问题上，运河河段上各监测站点在过去Th时间片上水质因子历史观测值是关键的影响因素。因此，以各监测站点过去Th时间片上水质因子历史观测值为依据，以此构建时空图来表征各监测站点之间的时空相关性。在某一时刻，构造一个Wvi向量，该向量包含站点vi过去Th时间片上待预测水质因子数据的平均值、标准差、偏度和峰度，我们根据站点vi与站点vj所构造的Wvi和Wvj，将得到的两向量之间皮尔逊相关系数ρWvi，Wvj作为站点vi和vj之间的时空权重关系，因此站点vi和vj所构成的邻接矩阵Avi，vj为：

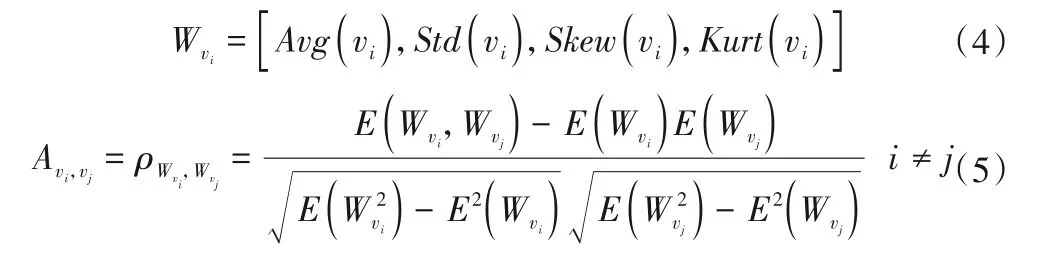
式中：Avg(vi)，Std(vi)，Skew(vi)，Kurt(vi)分别为监测站点vi过去Th时间片水质因子数据的平均值、标准差、偏度和峰度；E(Wvi)为向量Wvi的数学期望。

依据运河河段各监测站点在过去Th时间片水质因子的历史观测值，构造出各监测站点的时空图，见图2，圆圈表示运河河段上不同监测站点，两点之间的线段表示它们相互影响的强度，线段的颜色越深，代表影响程度越大。在空间维度上，如图2（a）、（b），可以发现运河上不同位置水质状态对c 点有不同的影响，甚至在同一位置随着时间的推移对c 点的影响也不同。在时空维度上，如图2（c），站点B 的水质历史观测值不仅对本身未来t+1 时刻水质状态有不同影响，而且对站点A 未来不同时刻的水质状态也会有不同的影响。那么预测未来运河河段上水质因子数据这一问题可以表述为：通过学习映射函数f(θ)，作用于Th周期内的各监测站点历史水质因子数据，来预测站点i未来Tp周期内水质因子数据［14］，即：

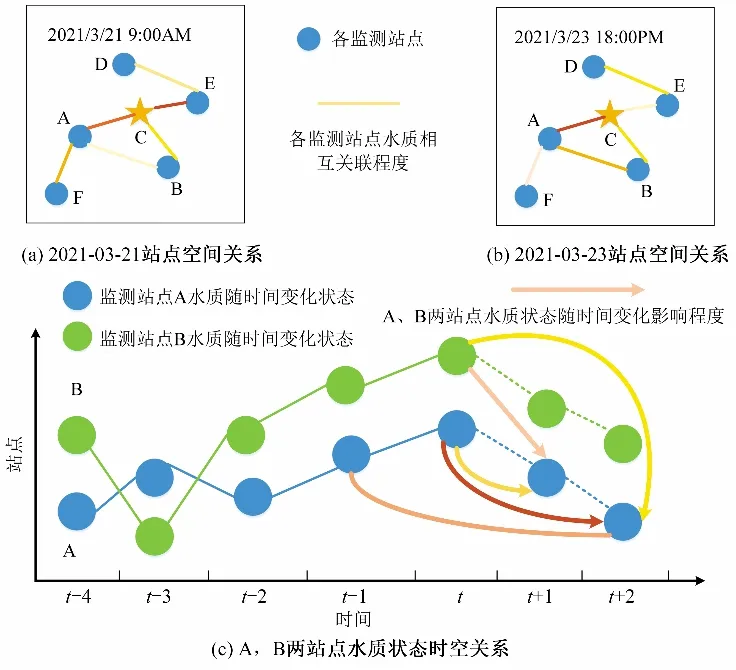
图2 运河河段不同位置的水质状态时空相关图Fig.2 Spatio-temporal correlation diagrams of water quality at different locations in the canal section

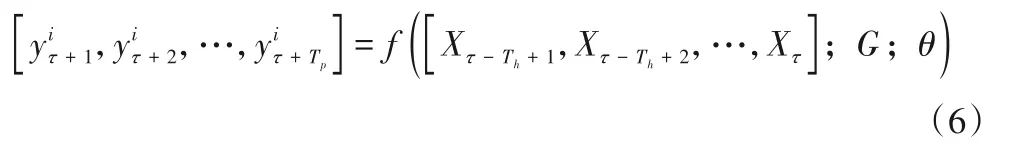
1.4 STG-LSTM 模型

STG-LSTM 模型用来实现运河河段不同位置水质因子的动态时空相关性，其总体架构如图3 所示。STG-LSTM 模型由时空模块和输出层组成，时空模块中包括图时空卷积模块和LSTM 的时间模块。图时空卷积模块由时空维度的图形卷积组成，从所构造的时空图中捕获运河上不同位置水质因子的空间相关性。基于LSTM 的时间模块经数据特征融合后提取相邻站点之间时间序列信息。最后，基于参数矩阵对两个输出变量进行时空特征融合，经过输出层得到最终的预测结果。

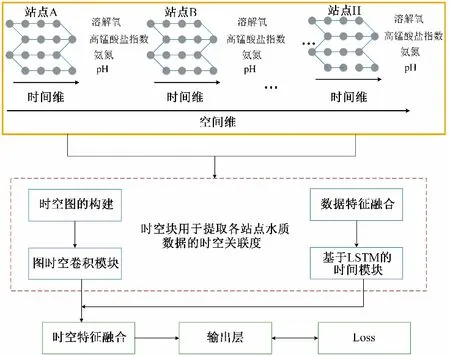
图3 STG-LSTM 的总体架构图Fig.3 STG-LSTM overall architecture diagram

1.4.1 图时空卷积模块

谱图理论将卷积运算从网格的数据推广到图结构数据上［15］。在本研究中，运河河段上各监测站点分布可以看成一个小型图形结构，每个站点上的特征可以看作图形上的信号［16］。因此，为了充分利用时空图的拓扑特性，在每一个时间片上采用基于谱图论的图卷积直接处理信号。

1.4.2 基于LSTM 的时间模块

从时间维度上看，运河河段水质因子数据本质上是二维的时间序列数据。根据相邻站点历史时刻水质因子数据，将其所构成的时空图输入到图卷积时空模块，用于捕捉各站点之间的空间相关性，但是在捕捉时间信息时会忽视相邻站点间水质数据历史时间的前后顺序。因此，选择长短记忆神经网络（LSTM），其可以克服在长期序列特征提取过程中出现的梯度消失和记忆衰减问题［17］。利用LSTM 对时间序列进行建模，用来提取相邻站点之间水质数据的时间序列信息［18，19］。首先，假设运河河段各站点监测的频率为q 次/d，当前时间为τ，预测窗口的大小为Tp，截取时间序列长度为Th，其中利用与预测周期直接关联的前一段历史时间序列，作为时间模块的输入，即χ =(Xτ-Th+1，Xτ-Th+2，…，Xτ) ∈RNFT。

1.5 方法评价指标

1.5.1 预测精度评价指标

（1）均方根误差（RMSE）。RMSE定义为均方根误差的平均根，计算公式如下。RMSE越小，预测精度越高。

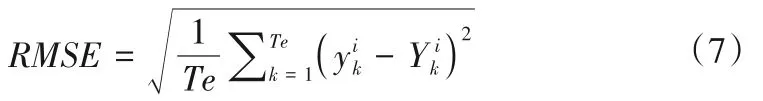
（2）决定系数（R2）。决定系数（R2）是回归平方和总偏差平方和的比率，反映因变量变化的自变量比例。R2越接近1，则说明预测精度越高。计算公式如下：

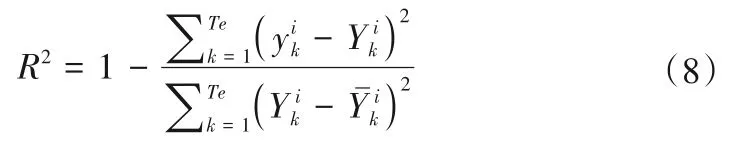
1.5.2 可靠性评价指标

可靠性验证预测值和观测值是否具有一致性。概率积分变换（PIT）值的统一均匀概率图用于评估预测可靠性。PIT 根据累积分布函数（CDF）和观测值计算的，计算公式如下。如果预测可靠，则PIT值在0和1之间服从均匀分布。均匀概率图中显示所有预测值，我们可以清楚的检查其是否服从均匀分布。

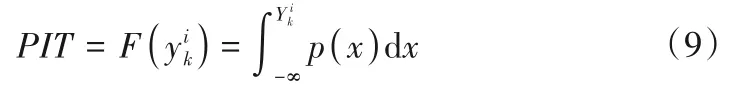
2 结果与分析

2.1 河流时空预测站点的选取

本文选用京杭运河常州段上8 个国控和省控监测站点，站点名称定义为A、B、C、D、E、F、G、H。为了找出与其余站点相关性最大的一个站点，作为时空预测站点。分别计算出每一个监测站点与其余监测站点溶解氧、高锰酸盐指数、氨氮、pH序列的最大互信息系数之和，见表2。

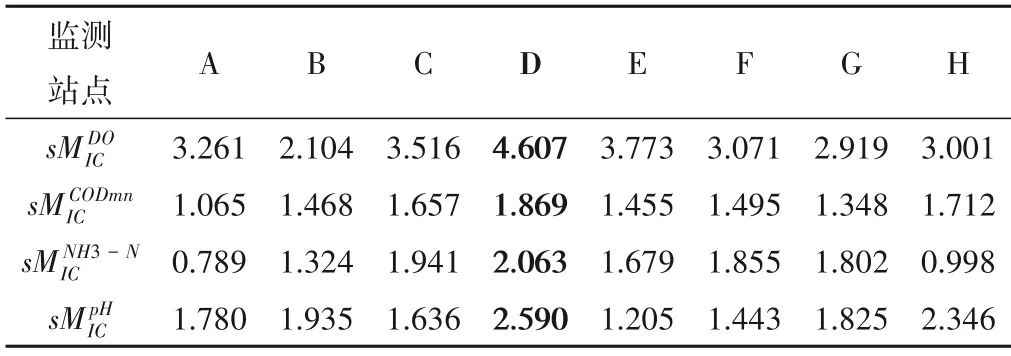
表2 8个监测站点4种水质因子MIC计算结果Tab.2 Calculation results of four water quality factors MIC at eight monitoring sites

2.2 验证STG-LSTM 收敛性

为了保证所提出的STG-LSTM 模型的预测精度，在比较之前首先验证其收敛性。用深度学习中常用的4种优化算法来验证模型的收敛性：自适应梯度算法（Adagrad）、均方根算法（RMSprop）、自适应增量算法（Adadelta）和Adam。将MSE 作为模型的损失函数，训练集作用于验证模型收敛性，站点D 溶解氧序列中的STG-LSTM 收敛曲线，见图4。随着迭代次数的增加，在后期所有优化函数的曲线都在同一条的水平线上，这表明迭代次数设置为1 000 次可以确保4 种优化算法能够在数据集中收敛。从溶解氧序列数据中我们可以看出，Adam 算法训练的MSE 虽然最后和RMSprop 算法相当，但是Adam 前期收敛速度更快，这表明Adam 算法在这四种优化算法中使STGLSTM收敛地更好。

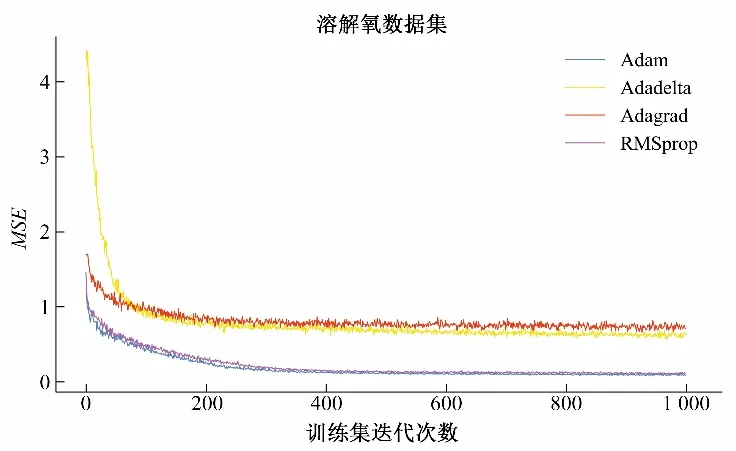
图4 STG-LSTM 的收敛曲线Fig.4 Convergence curve of STG-LSTM

2.3 实验结果

本研究做了3 组对比实验，实验中各模型通过Python3.7 基于tensorflow［20］和Scikit-learn［21］框架上进行搭建的。首先，SVR和GPR 作为解决时间序列数据的传统的机器模型，它们依靠本身核函数的特性，适合处理高维、非线性等复杂的回归问题且运行速度是它们的一大优势。因此，用SVR、GPR 与本文提出的STG-LSTM 模型相比较，从预测精度和运行时间两方面的综合表现来进行比较分析；其次，在深度学习中，LSTM 和GRU 通过添加门控机制来控制信息流以及状态和单元的更新，在时间序列预测的问题上能够获得很好的效果，但是它们只是提取了数据的时间依赖性，所以，本研究通过STG-LSTM 与LSTM、GRU 进行比较，旨在去验证在加入了空间维度后模型所表现出的优越性；最后，STDN 使用CNN 和RNN 分别建模提取数据时间和空间上的依赖性，并没有考虑时空维度上河流各个站点之间影响存在时间的滞后性。同样的STGCN 则通过图卷积和2D卷积分别捕获空间依赖性和时间依赖性，因此，将本文提出来的模型与STDN 和STGCN 进行比较，用来验证各站点数据时空特征融合后所构成的时空图，是否能够更好的表达时空维度上的依赖关系。

2.3.1 不同模型预测结果及验证

本组实验从预测精度和运行时间两方面来比较SVR、GPR和STG-LSTM。预测站点D 测试集溶解氧数据中这3 个模型的预测结果，见图5。预测值的R2越大、RMSE 越小，越接近于实际观测值，预测效果越好。从图5中可以看出，在预测一些突变点，STG-LSTM 模型的预测值比SVR和GPR更加的稳定。STGLSTM 的R2相较于SVR、GPR 分别提高0.053、0.052；RMSE 相较于SVR、GPR 分别下降0.315、0.313。说明本文模型相较于传统的机器学习模型对于河流水质因子预测更加具有优势，有着更好的预测效果。由于机器学习本身核函数的特性，SVR 和GPR训练时间相较于STG-LSTM大幅减少。

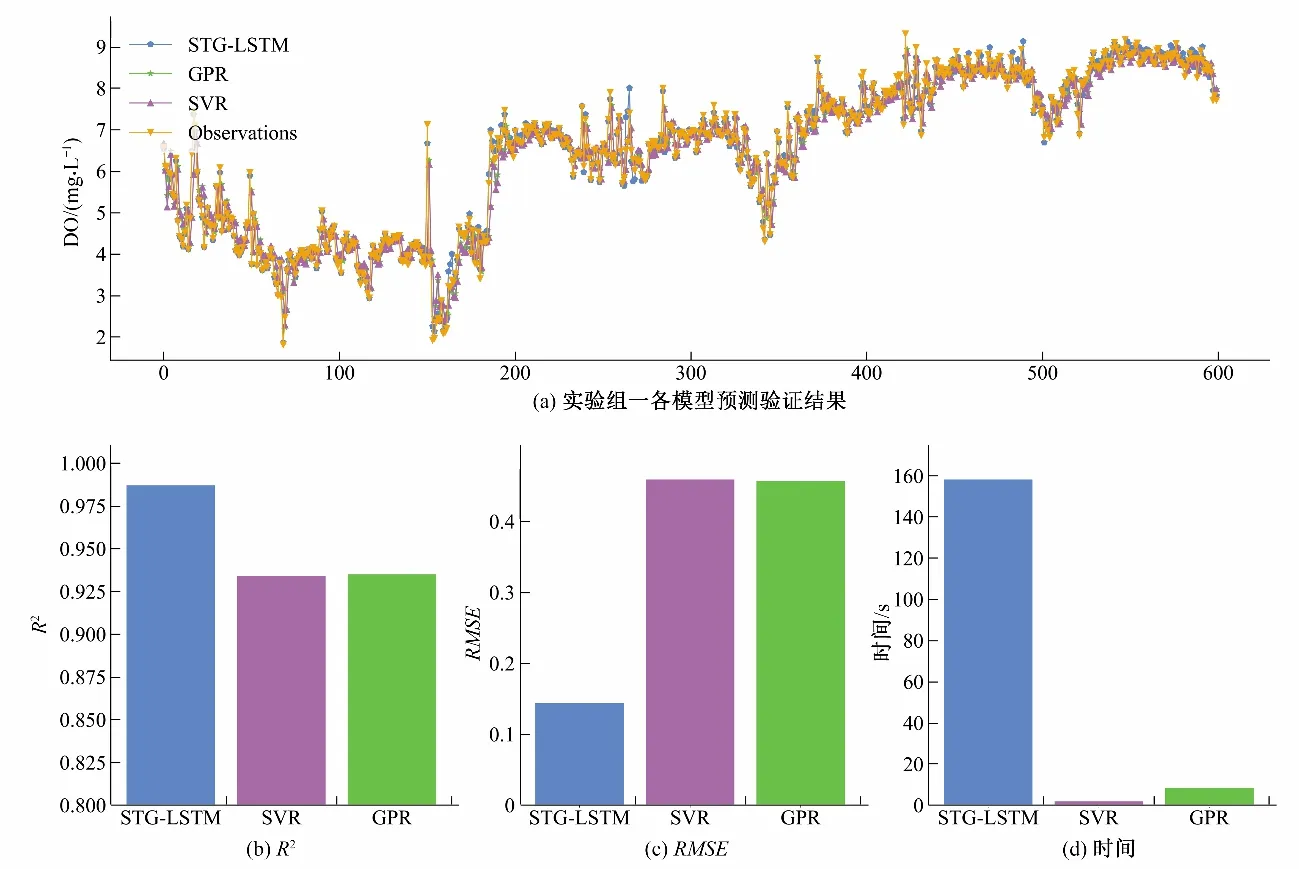
图5 SVR、GPR、STG-LSTM 在站点D上溶解氧序列预测结果Fig.5 SVR、GPR、STG-LSTM dissolved oxygen sequence prediction results on site D

本组实验用于验证在时间序列预测模型中增加空间关联信息能否有助于提高预测精度，并且去证明增加了空间关联信息后是否会显著增加模型的运行时间。LSTM、GRU、STGLSTM 这3 个模型在溶解氧测试集上的预测效果，见图6。本文模型对于溶解氧预测的效果均显著优于LSTM 和GRU，其R2和RMSE 分别为0.987 和0.144，R2相较于LSTM 和GRU 分别提高6.82%和7.17%；RMSE相较于LSTM 和GRU 分别下降69.30%和70.06%。这说明同时考虑时间关联和空间关联的方法优于仅考虑时间关联的方法，这是因为图卷积时空模块提取河流上预测站点与其余监测站点在每个时间片的空间关联特征，而融合时间序列模块进一步提取空间关联的时间关联特征，时空关联模块考虑了河流水质因子的时空分布特征。同时可以看出，本文提出的模型增加空间关联信息后并没有增加运行时间，3 个模型迭代的次数均为1 000 次，相反其运行的时间相较于LSTM和GRU 分别降低了9.2 s 和19.6 s。这是因为，MGCN-LSTM 能够快速从构建的时空图中得到各站点之间的时空关系。

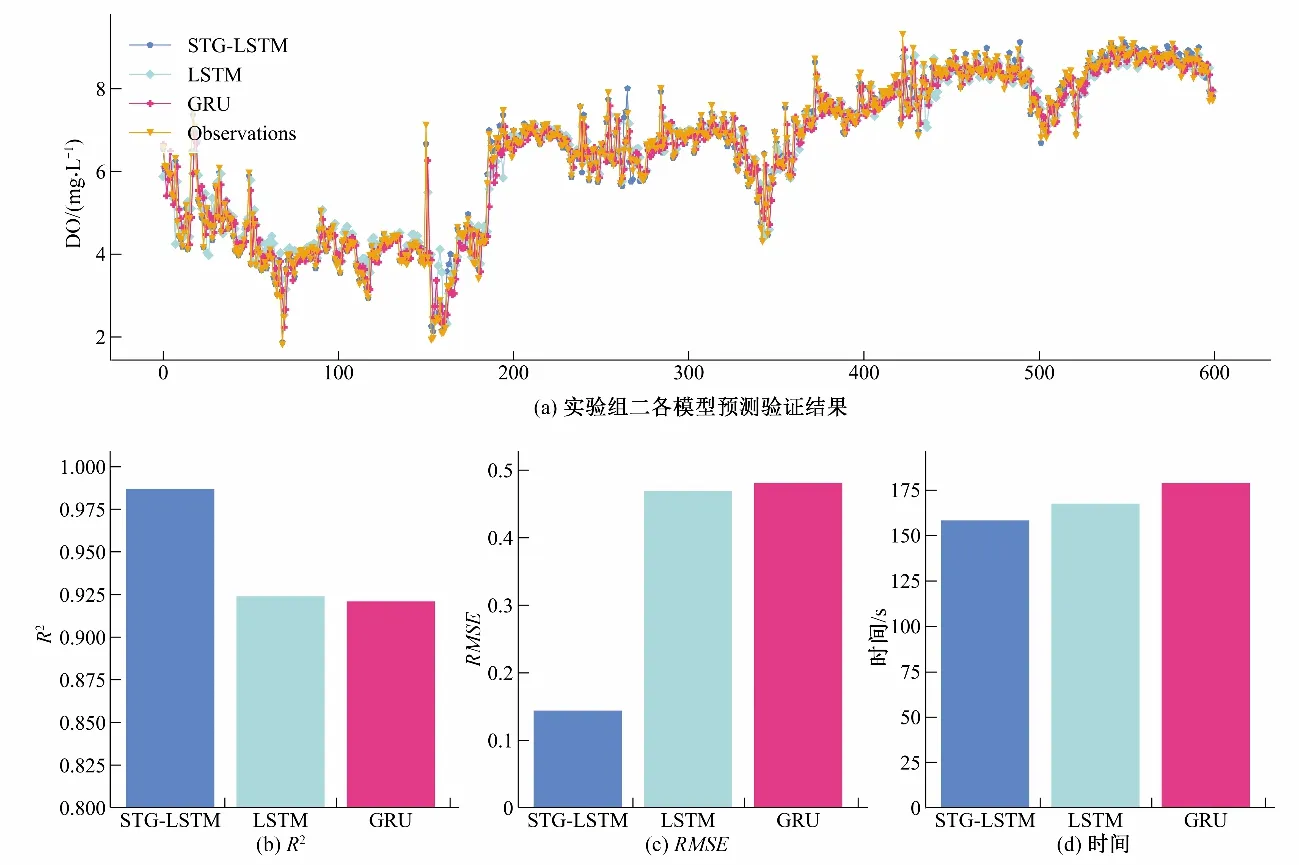
图6 LSTM、GRU、STG-LSTM 在站点D上溶解氧序列预测结果Fig.6 LSTM、GRU、STG-LSTM dissolved oxygen sequence prediction results on site D

本组实验用于验证水质因子时空图是否能够更好地表达时空维度上的依赖关系。STDN、STGCN 和STG-LSTM 三个模型的预测效果，见图7。STG-LSTM 对于溶解氧预测精度相较于STDN 和STGCN 略高，其R2相较于STDN 和STGCN 分别提高4.45%和2.07%；RMSE则相较于STDN 和STGCN 下降67.86%和28.71%。STDN 运行时间相较STG-LSTM 大幅下降，这是因为虽然STDN 也是分别提取了数据之间的空间和时间的依赖性，但是CNN 只能捕获网格结构数据上各位置局部的空间相关性，这里并没有考虑其余站点的空间信息。STGCN 没有使用时空图，而是根据站点之间的数据信息构建空间图进行计算的。综上所述，本文提出的STG-LSTM 通过时空特征融合所构的时空图，能够更好地表达时空维度上的依赖关系，从而提高了模型预测精度。

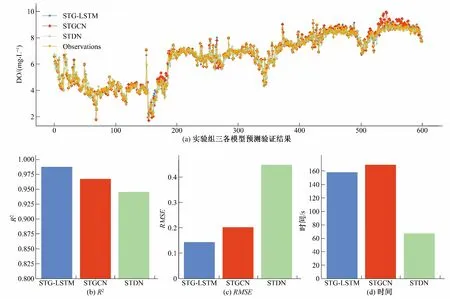
图7 STDN、STGCN、STG-LSTM 在站点D上溶解氧序列预测结果Fig.7 STDN、STGCN、STG-LSTM dissolved oxygen sequence prediction results on site D

2.3.2 河流不同位置水质预测结果

在上述3组实验中对所选择的时空预测站点溶解氧序列做了预测，并将本文模型从预测精度和训练时间综合和6 种模型进行了比较，可以看出本文提出的模型在时空预测上面具有良好的预测效果。因此，选用STG-LSTM 模型，依据构造的时空图，表征出各监测站点的时空相关性，对运河河段其他监测站点的水质因子序列进行预测，从而得到未来一段时间运河河段不同位置的水质状态。关键的是，由于构造出各监测站点的时空图，STG-LSTM 只需要运行一次，就能同时得到运河河段8 个监测站点的预测结果，相比与其他模型单次运行只能得到单个站点预测结果，大大缩短了训练的时间。以溶解氧序列为例，STG-LSTM对运河河段不同站点预测结果的R2、RMSE，见图8。

从图8可知，选择的时空预测站点D 预测效果最好，因为该站点更容易获取其他站点的水质状态信息。不同站点从其他站点所获得的水质状态信息是不相同的，导致运河河段不同位置的水质状态信息预测效果也不相同的。综上所述，本研究提出的STG-LSTM 模型根据不同监测站点所构造的时空图，能够快速对未来运河河段不同位置的水质状态做出预测，并得到较好的预测效果。

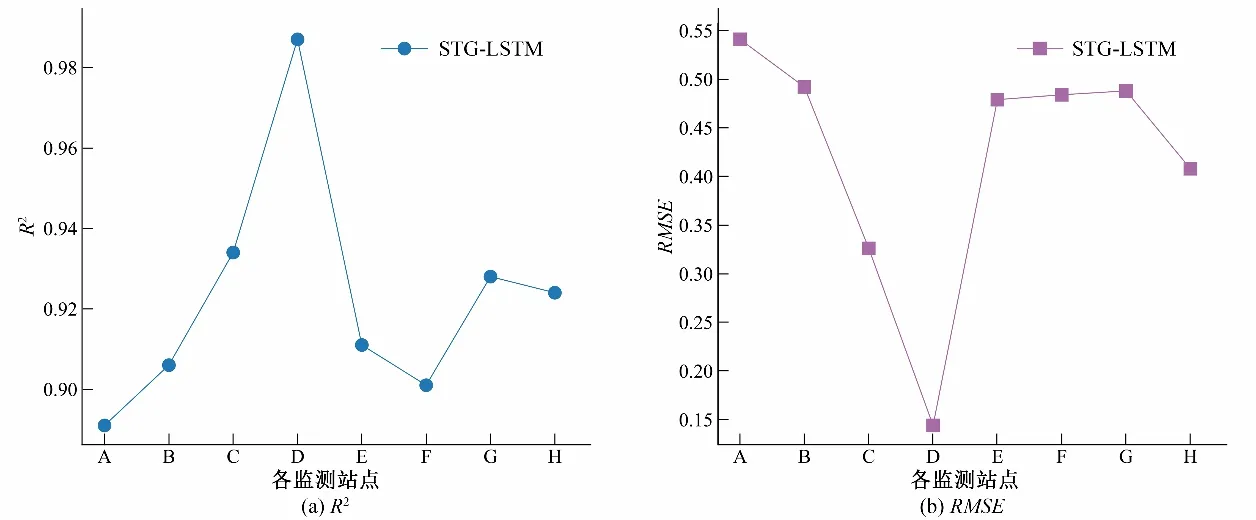
图8 STG-LSTM 模型在8个站点上溶解氧序列预测效果曲线Fig.8 The STG-LSTM model's dissolved oxygen sequence prediction effect curve on eight stations

2.4 模型验证

2.4.1 STG-LSTM 模型可靠性验证

从预测精度和模型的训练时间两方面对STG-LSTM 的预测结果进行评价后，并继续对其进行可靠性检验，以确保预测结果是具有说服力的。首先，将站点D 溶解氧序列的测试集分成4 组，每组150 条数据。其次，计算出每组数据每次观察的PIT值，如果这些值是服从均匀分布的，则说明提出的模型预测结果是可靠的。因此，绘制了这4 组测试集PIT 值的均匀概率图，可以清楚地看到这些值是否服从均匀分布，见图9。第一组和第三组数据集的PIT 值是沿着对角线均匀分布，其范围均匀覆盖［0，1］，所有的点都在Kolmogorov 5%显著性带内，这表明所预测的PDF 不是过高或过低，也不是过宽或过窄。第二组和第四组数据集的PIT 值振荡的幅度要稍微大一些，有部分点在Kolmogorov 5%显著性带外，是由于这两组数据集中某些点对应的观测值存在异常，或者是该预测的站点对应的部分观测值与其余站点的观测值关联度不是很高。但是，这两组数据集的PIT 值大部分还是沿着对角线均匀分布的。因此，STG-LSTM的预测结果是可靠的令人信服的。

图9 STG-LSTM 模型对站点D溶解氧序列的可靠性验证结果Fig.9 Reliability verification results of STG-LSTM model on the dissolved oxygen sequence of site D

2.4.2 STG-LSTM 模型普适性检验

以上实验证明STG-LSTM 对河流溶解氧序列数据预测取得很好的预测效果。为了检验模型的普适性，对时空预测站点D 上其余3 种水质因子做了相同实验并与其余6 种模型进行对比。4 种不同水质因子数据集中7 个模型的预测指标，见表3。TT 是模型训练时间的缩写。就预测精度而言，STG-LSTM 在四种水质因子数据集中预测效果最好，预测效果可以在RMSE 和R2这两个指标中体现。在TT 的指标中，STG-LSTM 相较于STDN、STGCN、LSTM、GRU，训练时间仅比STDN 长，但是STGLSTM只需运行一次，就能得到8个监测站点的预测结果。这是因为构造的时空图能够得到各监测站点之间的时空关联性。尽管SVR、GPR 的TT 值特别小，但它们的预测精度是有限的。在实际应用中，STG-LSTM 可以多次运行，以最佳结果作为预测结果。在上述这些指标中可以证实，STG-LSTM 对于河流不同水质因子数据预测具有较高的预测精度和一定的普适性。