元胞自动机在两类传染病模型中的应用

张睿洋

（华南师范大学，广东 广州 510631）

0 引 言

疾病传播模型主要包括SI 模型、SIR 模型、SIS 模型、SEIR 模型等几类。其中，SI 模型是将人群划分易感状态（S）和感染状态（I）两类。易感人群在单位时间会以的传染概率被感染人群感染。该模型的缺陷是并未考虑到感染人群被治愈移除的情况，在本文专门用以讨论密闭空间的人群感染情况。SIR 模型在SI 模型基础上考虑了移出状态（R），对应疾病被治愈或死亡的状态，感染人群在单位时间会以的传染概率由感染状态转移至移除状态。该模型较为符合现实情况，但缺少了携带病毒的处于潜伏状态的人群。SIS 模型则考虑了重复传染的情况，被治愈的人群还会在单位时间以的传染概率由感染状态转移至易感状态。SEIR 模型在SIR 模型基础上考虑了潜伏状态（E），其中易感状态在单位时间以传染概率转移至潜伏状态，而潜伏状态在单位时间以的传染概率转移至感染状态。SEIR 传染病模型，最为贴近现实情景，适用领域最为广泛，被众多学者运用于HIV、SARS、新冠等传染病的分析，在本文运用于对新冠肺炎病毒问题的讨论。

元胞自动机（cellular automata，CA）是一种时间、空间、状态都离散，空间相互作用和时间因果关系为局部的网格动力学模型，具有模拟复杂系统时空演化过程的能力，相比其他模型可以较好地仿真出传染情况，该类研究对调控新冠疫情具有重要意义，其中谭欣欣等人考虑了个体移动的异质性，个体的感染率符合（0，1）的均匀分布，并与欧氏距离有关；郑三强等人构造了传染中心疫区的高斯压力死亡模型，考虑了人口的流动特征；王燕考虑了病毒的接种率，运用元胞自动机仿真无病的平衡点。

本文从基础的SIR 模型开始，讨论封闭环境与非封闭环境两种情况下病毒的传染情况。

1 封闭条件下的SI 模型

1.1 元胞自动机介绍

按照元胞自动机的定义，用数学符号来表示，元胞自动机可以视为由一个元胞空间和定义于该空间的变换函数所组成。元胞自动机用形式语言的方式来描述，可以用一个四元组表示：=（L，，，）。

在这里，代表一个元胞自动机系统，L代表一个规则划分的网格空间，代表元胞的邻居集合，表示一个将S映射到上的一个局部转换函数，即根据时刻某个元胞的所有邻居的状态组合来确定+l 时刻该元胞的状态值。

1.2 模型参数

模型参数如表1所示。

表1 模型参数

1.3 模型准备

封闭条件下我们只考虑S 人群（易感人群）与I 人群（感染人群），探究短时间内封闭环境下的感染情况。以二等车厢的高铁（100 个座位为例）。

由文献[4]，新冠病毒在列车之中各行之间的平均攻击率不同（P ＜.001）。与索引患者在同一排座位上的乘客的平均发作率为1.5%（142/9 299；95%CI，1.3%～1.8%），比相隔1 排和2 排的座位高出大约10 倍。但是，相隔1 排和2 排的座椅之间的传播风险没有显著差异。尽管相隔3 行的座椅有传播COVID-19 的风险，但这种攻击率大约是相隔1 行和2 行的座椅感染风险的一半，具体数据如表2所示。

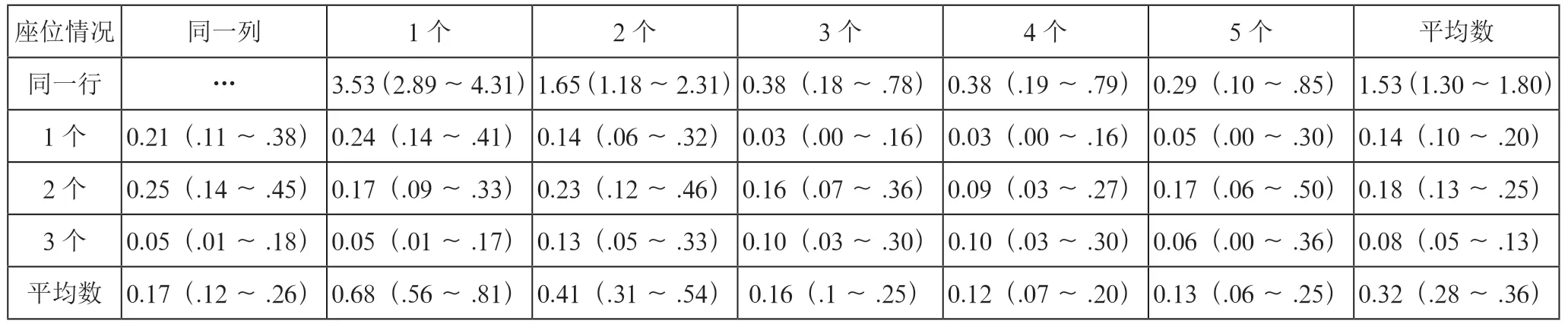
表2 乘客相对位置感染率 单位：%

1.4 模型建立

本研究模型构架为：

（1）元胞：本列车的所有人群；

（2）元胞空问：=10×10 的二维空间；

（3）邻居形式：邻居半径为1 的Moore 型；

（4）元胞状态空间：设元胞的状态变量为C（，），表示第行第列元胞在时刻的状态。本模型将C（，）规定状态如下：

其中E（，）表示第行第列被病毒攻击概率，设初始传染人位于第5 行第5 列，如图1所示。

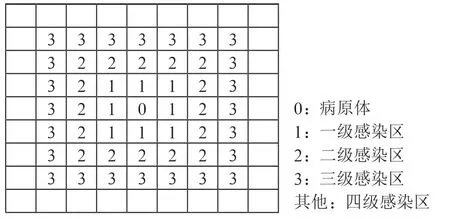
图1 感染区示意图

（5）元胞状态更新规则：

1）判断元胞所处感染区的位置：

若C （，）=0，该元胞为病原体，具有传染性。

若C （，）=1，该元胞位于一级传染区，有较大概率在+1 时刻转化为病原体，即C （，）=0。

若C （，）=2，该元胞位于二级传染区，有一定概率可能在+1 时刻转化为病原体，即C （，）=0。

若C （，）=3，该元胞位于三级传染区，有较小概率可能在+1 时刻转化为病原体，即C （，）=0。

若C （，）=4，该元胞位于四级传染区，有极小概率可能在+1 时刻转化为病原体，即C （，）=0。

2）元胞更新状态后再次检查元胞所处感染区的位置。在+1 时刻元胞所处感染区可能发生变化，重新判断元胞所处感染区，再次抽取随机数判断各元胞是否被感染。

3）重复状态更新，得出结果。重复上述1）、2）的操作，进行多次状态更新与判断，计算时刻C （，）=0（1≤，≤10）的数量，得到仿真结果。

程序逻辑如图2所示。

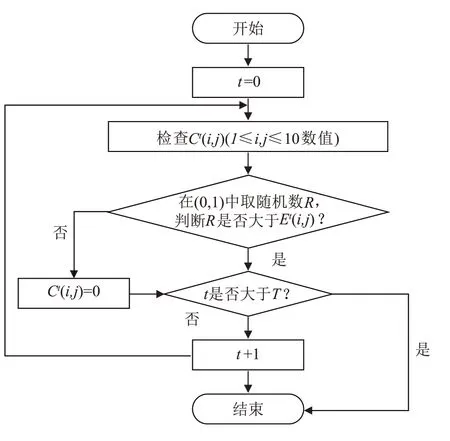
图2 SI 模拟仿真逻辑图

1.5 模型仿真结果与分析

取人数为60、80、100，仿真模拟100 次，每一次总时间分别为2 h、3 h、4 h 记录出现感染人数的次数，仿真结果如图3～8 所示。

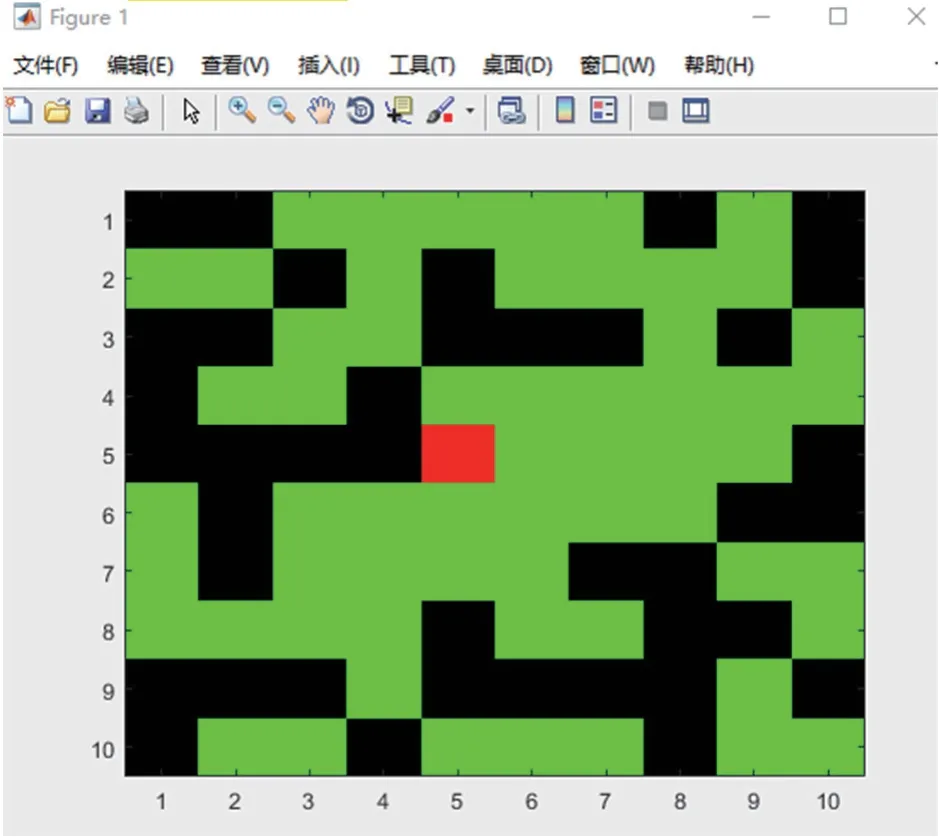
图3 人数n = 60 人，时间t = 2h 模拟结果图

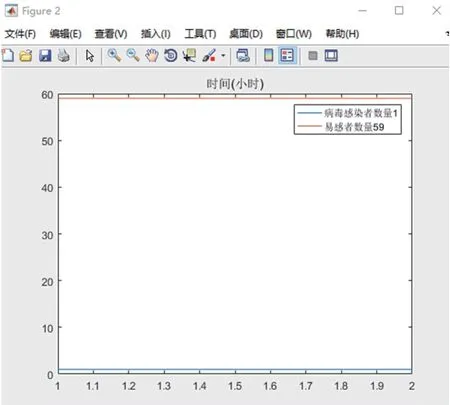
图4 人数n = 60 人，时间t = 2h 模拟过程详情

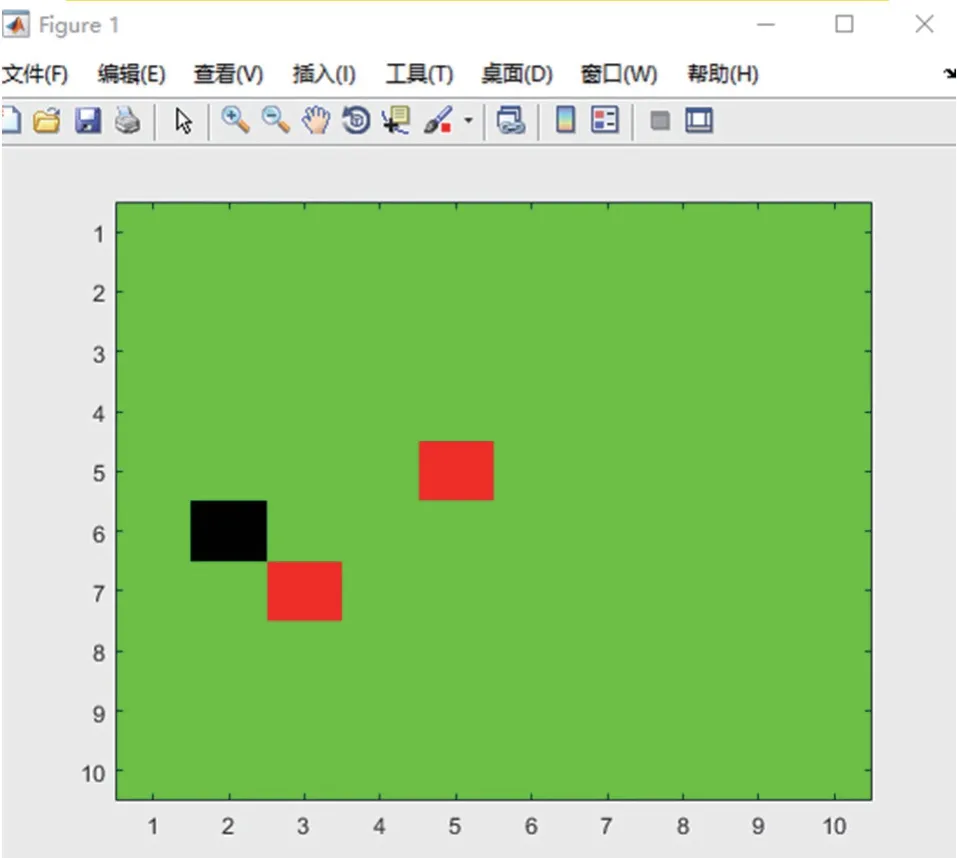
图5 人数n = 99 人，时间t = 2h 模拟结果图

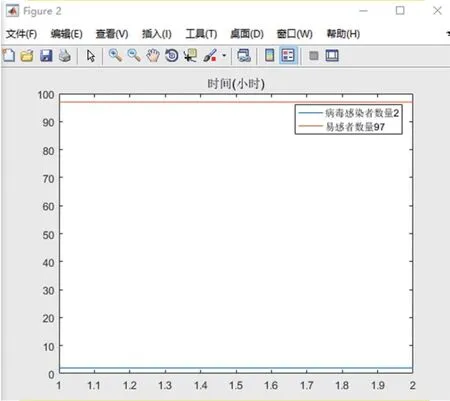
图6 人数n = 99 人，时间t = 2h 模拟过程详情

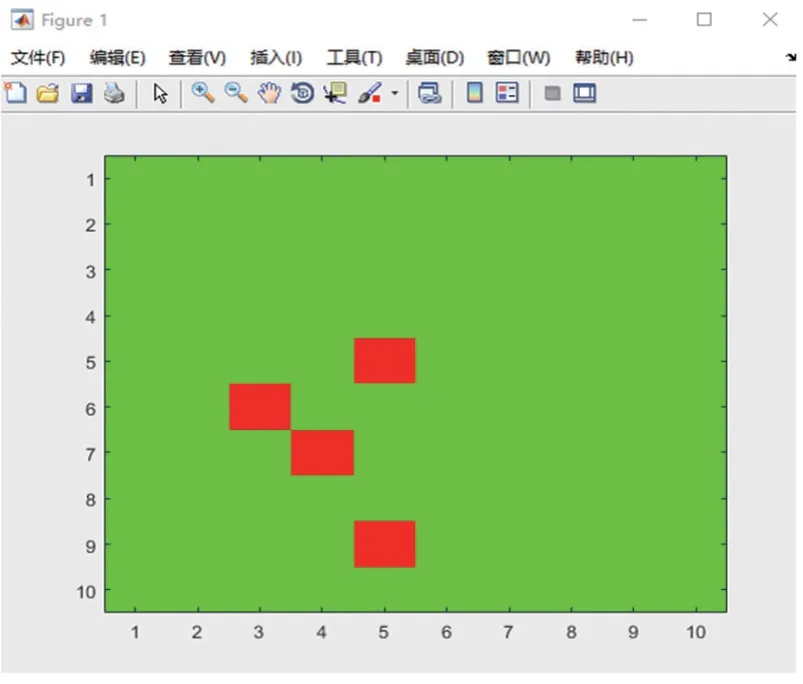
图7 人数n = 100 人，时间t = 4h 模拟结果图

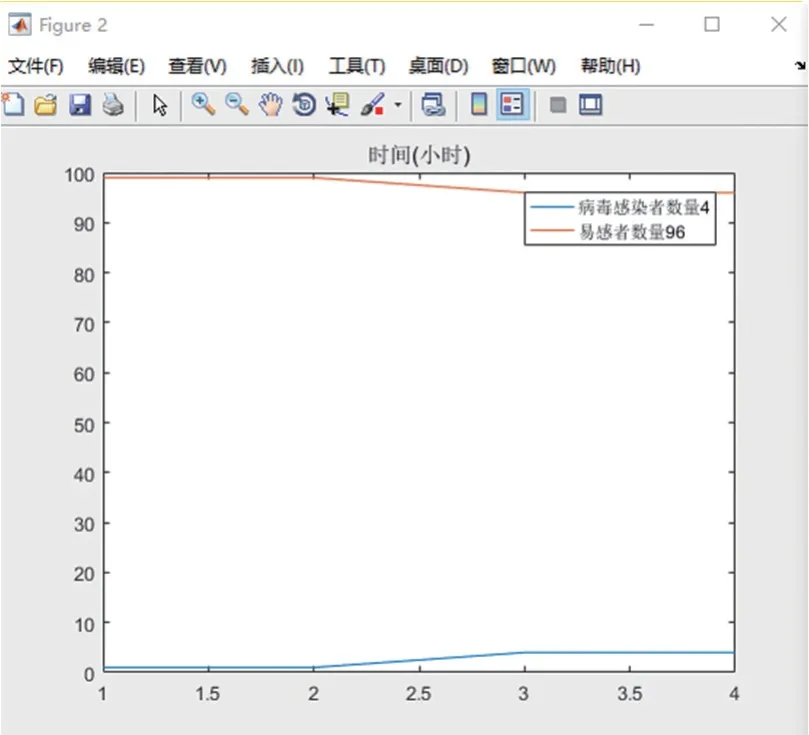
图8 人数n =100 人，时间t = 4h 模拟过程详情

当仅为2 h 时，60 人的车厢出现第二位感染者的概率为13%，80 人的车厢为21%，而100 人的车厢出现感染者的概率接近35%，且更容易出现第3、4 位感染者。

当行车时间为4 h 时，每种情况感染概率均提升10%以上，其中100 人的车厢提升最为明显，甚至出现第六位、第七位感染者。

综上，根据元胞自动机的仿真模拟结果，减少行车时间，同时高铁尽量压缩行车人数，减少人口密度，是防疫的必要条件。同时，设立每个座位之间的隔离措施，降低一级感染区的风险，也能够大大提高乘客的安全。

2 非封闭条件下的SIR 模型

2.1 模型的准备

本模型根据1 中模型改进而来，在1 的基础上引进两类人群，注重两两之间状态转移的概率，根据仿真结果得出相应结论，并结合石家庄疫情进行分析。

根据传统的SEIR 模型，病毒扩散规则如图9所示，满足：

图9 人群转化示意图

（1）易感者人群与潜伏期人群接触，潜伏期人群邻与范围内的易感者有一定的概率感染为潜伏期人群。

（2）移除人群不再有感染的可能，包括治疗成功的人群与死亡的人群。

（3）潜伏期人群有一定概率转化为患病人群。

以编号0 表示易感人群，编号1 表示潜伏期人群，编号2 表示患病人群，编号3 表示移除人群。用符号P表示状态转移概率，其中，=0，1，2，3。

取新冠肺炎潜伏期中位数4 天，即潜伏期到发病的概率取0.25；因为平均出院日期大概为10 天左右，故患病人群转换为移除人群概率取0.1；当易感者与传染性个体接触时，统一接触率为0.06；易感者转换为患病人群概率取0.001。

2.2 模型参数

模型参数如表3所示。

表3 模型参数

2.3 模型的建立

以一个非封闭的广泛地区为例进行模拟，本模型规定（，）如下：

元胞状态规则更新如下：

确定A（，）与S（，）数值：

（1）判断元胞所处感染区的位置，元胞状态更新。

（2）元胞更新状态后再次检查元胞所处感染区的位置。

（3）重复状态更新，得出结果。

重复上述（1）（2）的操作，进行多次状态更新与判断，分别计算时刻（i，）=0，1，2，3 的数量，得到仿真结果。

程序逻辑如图10 所示。

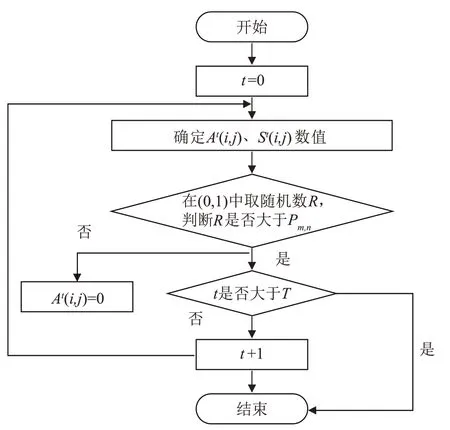
图10 SEIR 模型模拟仿真逻辑图

2.4 模型仿真结果与分析

采取800×800 的元胞空间用于容纳占地面积与人口，人口总数取16 万人，迭代周期取20 天，并且易感人群转换为潜伏人群的概率分别取0.1，0.2，0.3，仿真结果如图11 ～16 所示。

图11 P0，1=0.1 模拟结果图

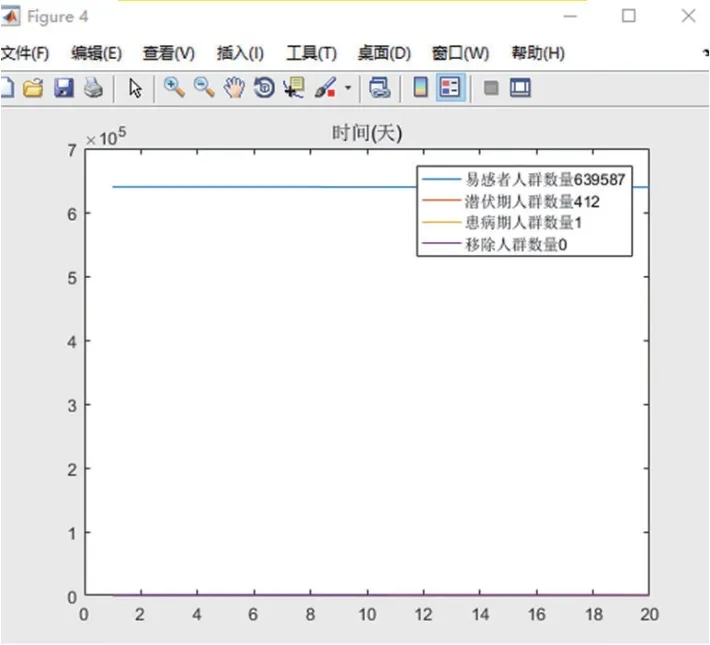
图12 P0，1=0.1 模拟过程详情

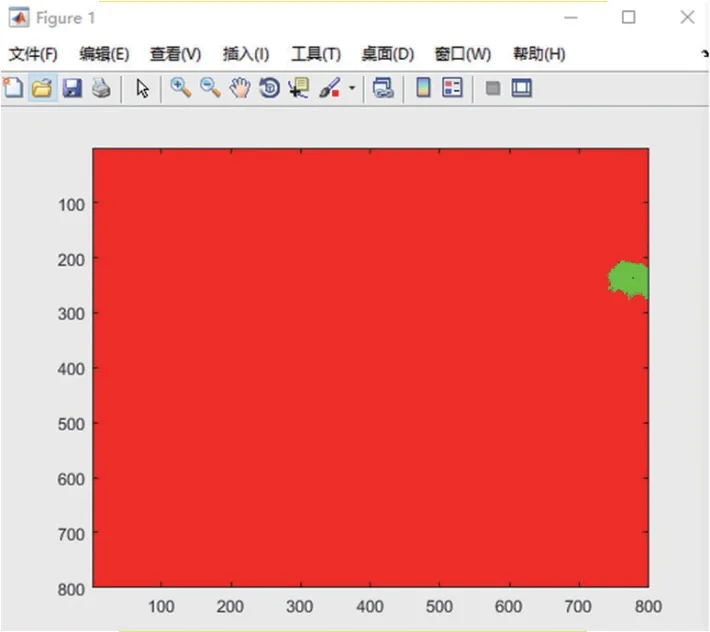
图13 P0，1=0.2 模拟结果图

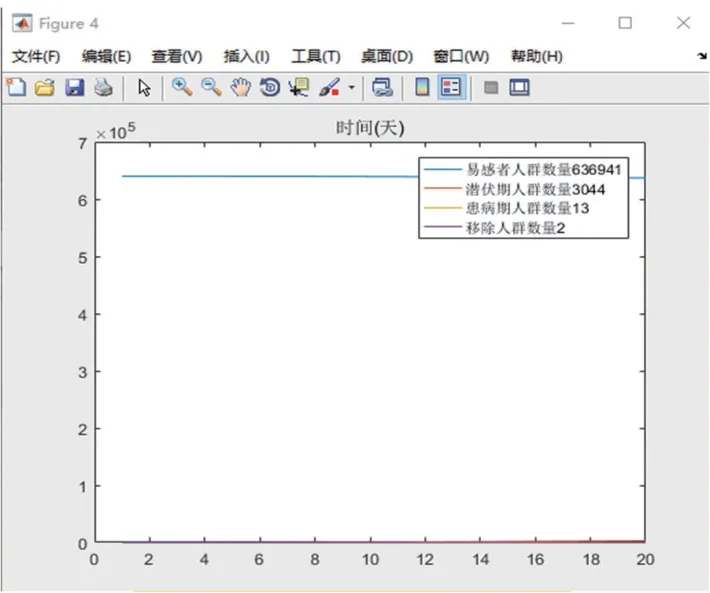
图14 P0，1=0.2 模拟过程详情

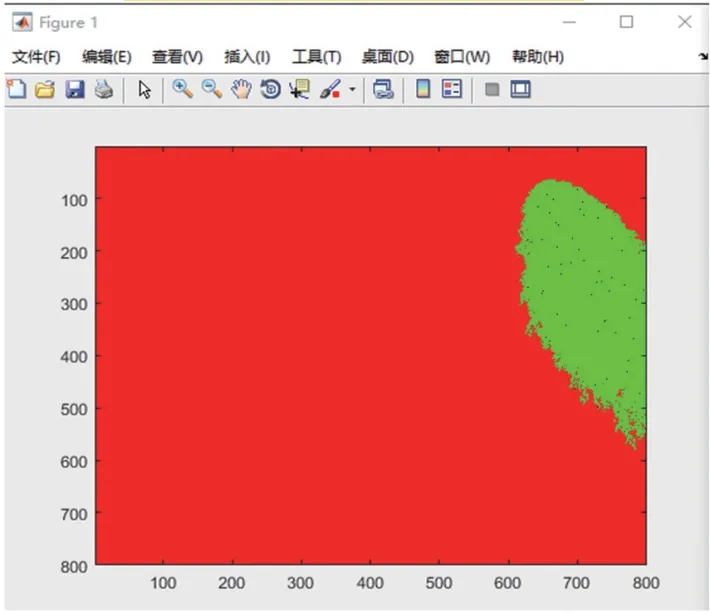
图15 P0，1=0.3 模拟结果图

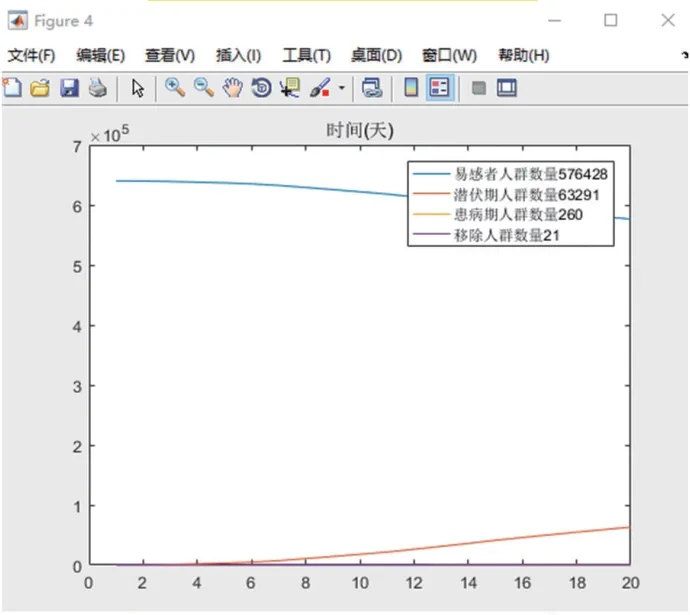
图16 P0，1=0.3 模拟过程详情

当=0.1，最终感染人群不过1 000 人；当=0.2，最终感染人群在2 000 ～6 000 人范围内浮动；=0.3，最终感染人群在2 万～7 万的人数浮动。

显而易见，当感染率越大时，感染人数浮动越大，这与政府的政策支持与群众的自主性密不可分，需要明确地制定减少易感者与潜伏期人群的接触率的措施与方针。除了减少易感者有效接触之外，延缓疫情的空间扩散关键在于对潜伏者的控制，这主要在于外部压力，从涉外人员以及物品等方面进行严格管控加强检查力度，提高潜伏者检出率，尽早隔离同时提高患者的就诊与收治能力。

在模拟仿真的结果中，也能很明显地发现在仅有一位初始感染者的条件下，感染人群呈现群落态分布，而在有两位初始感染者时，分为两个群落状分别扩散，如图17、18 所示。这也符合我们疫情防控的客观事实，在疫情出现时尽早封锁，防止病情的扩散。

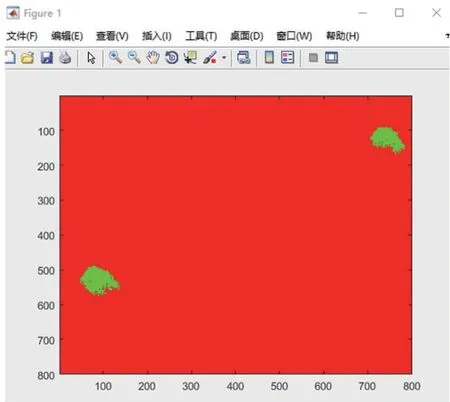
图17 初始感染者数n=2，P0，1=0.2 模拟结果图

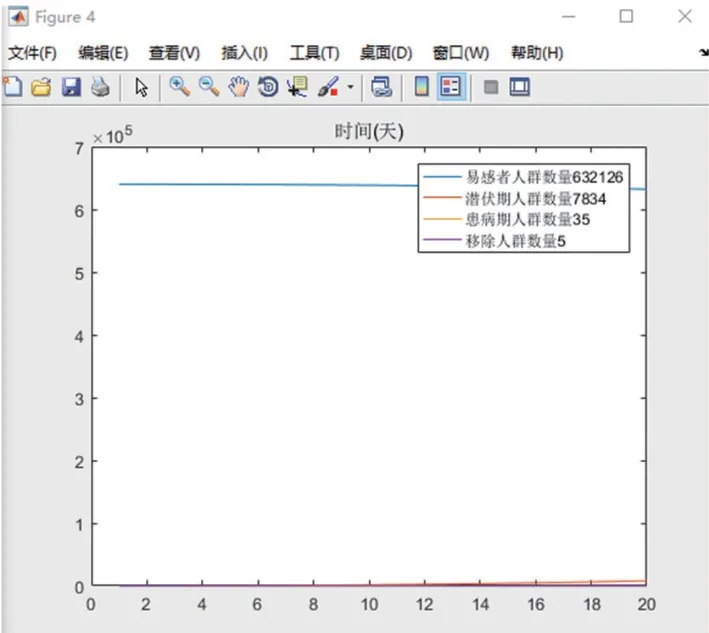
图18 初始感染者数n=2，P0，1=0.2 模拟过程详情

3 结 论

论文从封闭环境与非封闭环境、短期与长期几种情况来利用元胞自动机进行模拟仿真，得出了相关结论，符合客观事实。

实际上，本文提出的元胞自动机较为基础，在该理论上可以添加各种因素，让结果更加符合客观的事实，例如考虑人口的流动性，设置规则让每一个方格状态与邻近的方格状态进行替换，引入高斯压力死亡模型等，更加直观地探索传播规律。更进一步，与现实的疫情数据进行拟合，结合相应的地理示意图，对数据信息进行还原，真正地让数据回归现实，得到意义。