静态与动态场景下视觉里程计定位精度优化方法

谢 波，孙一杰，张国良

（1.四川轻化工大学自动化与信息工程学院，四川 宜宾 644000；2.人工智能四川省重点实验室，四川 宜宾 644000）

引 言

视觉里程计[1]是视觉SLAM[2-4]的重要组成部分，因为它能够通过视觉传感器获取的视觉信息进行实时位姿估计，所以广泛应用于各个领域[5-7]中。而视觉里程计的应用领域几乎都要求系统具有较高的定位精度，所以提升视觉里程计的定位精度成为此领域内的一大重点任务。

传统的视觉里程计最常用的两种方法为特征点法和直接法。特征点法首先从视觉传感器获取的图像中提取SIFT[8]、SURF[9]、ORB[10]等特征点，然后根据对极几何求解基础矩阵或PnP[11-13]与ICP 的方法[14]估计相机位姿。基于特征点法，Henry 等[15]利用RGB-D 相机采集周围环境中的图像数据，并提取图像中的SIFT 特征点，然后利用RGB-D 图像的深度信息恢复空间路标点，最后用ICP 方法估计相机位姿。与Henry 等[15]有所不同，Endres 等[16]在图像中提取SURF特征点，并用一种改进的ICP方法估计相机位姿。Mur-Art 等[17]提出了ORB-SLAM2 算法，该算法提取图像中带有描述子的ORB 特征点，较好地提高了基于特征点法的视觉里程计的定位精度。直接法是基于帧间同一像素坐标处像素点灰度值不变这一假设提出的，该方法直接将上一帧图像的相机位姿作为初值，通过最小化帧间特征点的像素点灰度误差目标函数得到相机位姿。基于直接法，Engel 等[18]提出了LSD-SLAM 算法，该算法将SLAM系统运用到地图重建领域，最终很好地完成了地图的半稠密重建，但是该算法并没有提高视觉里程计的定位精度。之后，有学者提出了一种更为实用的直接法视觉里程计系统（DSO）[19]，该方法能够估计相机的曝光参数，并提出了光度标定，保证系统在相机曝光时间变化时也能正常使用。GAO 等[20]在DSO 系统基础上添加了回环部分，使DOS 系统成为一个完整的SLAM系统。

以上文献都在提高视觉里程计系统性能上做出了较大的贡献，但依靠直接法或特征点法所提出的视觉里程计方法仅仅利用单一误差项对相机位姿进行优化，没有考虑将其他更多误差项联合起来对相机位姿进行多重优化。为此，本文在不同视觉传感器（单目（Mono）、双目（Stereo）和R-GBD 相机）与不同场景（静态和动态）下，利用多种误差项对相机位姿进行优化，从而提高视觉里程计的定位精度。在静态与动态场景中，本文分别提出了最小化重投影像素点灰度误差与最小化深度误差方法，并将它们与传统的最小化重投影像素点坐标误差方法结合，对相机位姿进行优化。

1 系统框架

针对静态场景和动态场景提出了两种不同的视觉里程计系统框架，并在最小化重投影像素坐标误差方法的基础上，分别融入了本文所提出的最小化重投影像素点灰度误差与最小化深度误差方法对相机位姿进行优化，最小化误差目标函数的方法统一使用列文伯格-马夸尔特算法。系统框架如图1所示。图1（a）和1（b）分别为静态与动态场景下的系统框架。两个系统框架工作原理类似——在完成系统初始化后，首先完成当前帧图像的特征提取和当前帧与参考帧之间的帧间特征匹配，只是在对相机位姿进行优化时所选用的方法策略有所不同。

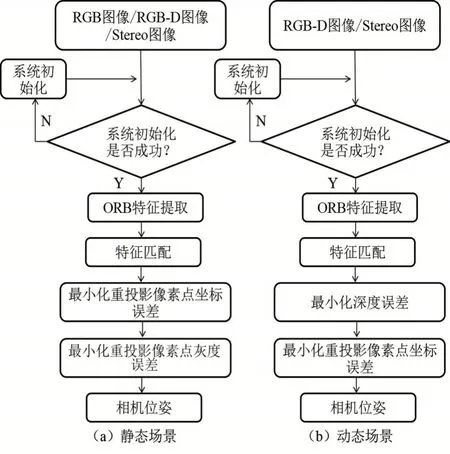
图1 系统框架图

对于静态场景，首先根据最小化重投影像素点坐标误差得到相机位姿初值，然后利用上一步所得的相机位姿初值，通过最小化重投影像素点灰度误差得到最终估计相机位姿。对于动态场景，首先根据最小化深度误差得到相机位姿初值，然后利用上一步所得的相机位姿初值，通过最小化重投影像素点坐标误差得到最终估计相机位姿。

2 系统流程

2.1 坐标系定义

如图2 所示，定义了世界坐标系w 系和相机坐标系c 系来描述相机的运动姿态，两个坐标系均符合右手准则。其中世界坐标系固定不动，相机坐标系随相机位姿变化而改动。对于空间路标点P来说，它在世界坐标系下的坐标与在相机坐标系下的坐标是不同的，因此用变换矩阵T来描述空间路标点在不同坐标系间的坐标变换。

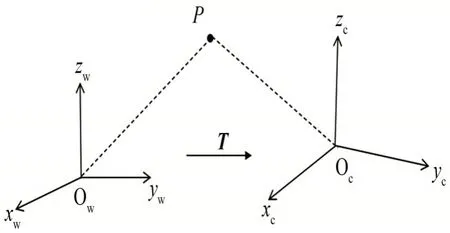
图2 坐标系示意图

2.2 系统初始化

无论是单目相机、双目相机还是RGB-D 相机，初始化的流程都大致相同。首先，对输入图像提取ORB 特征点（双目只提取左目图像），特征点数目大于阈值的图像将被设置为关键帧，并存储在关键帧库中。其次，通过当前关键帧与上一关键帧之间的帧间特征匹配获得特征点匹配点对。然后，利用所获得的特征点匹配点对，根据对极约束获得基础矩阵或本质矩阵，并对矩阵进行奇异值分解，求得相机位姿。最后，通过三角化的方法恢复匹配点对的空间路标点坐标，并计算当前帧所有空间路标点的词袋向量[21]。

2.3 ORB特征提取与特征匹配

初始化完成后也需要对每一帧图像提取ORB特征点。与初始化时不同之处在于，初始化后特征点数目超过阈值的图像不一定会成为关键帧，是否能成为关键帧取决于当前帧追踪到的空间路标点的数目及上一次插入关键帧的时间等因素。完成特征点的提取之后，和初始化一样，计算当前帧所有特征点的词袋向量[21]，以减小特征匹配所损耗的时间。

图3 所示为词袋向量计算原理图，图中的字典是将很多图像特征点的描述子用K-means 聚类扩展方法[21]离线生成的，其中每个节点有k条分枝，一共有d层。

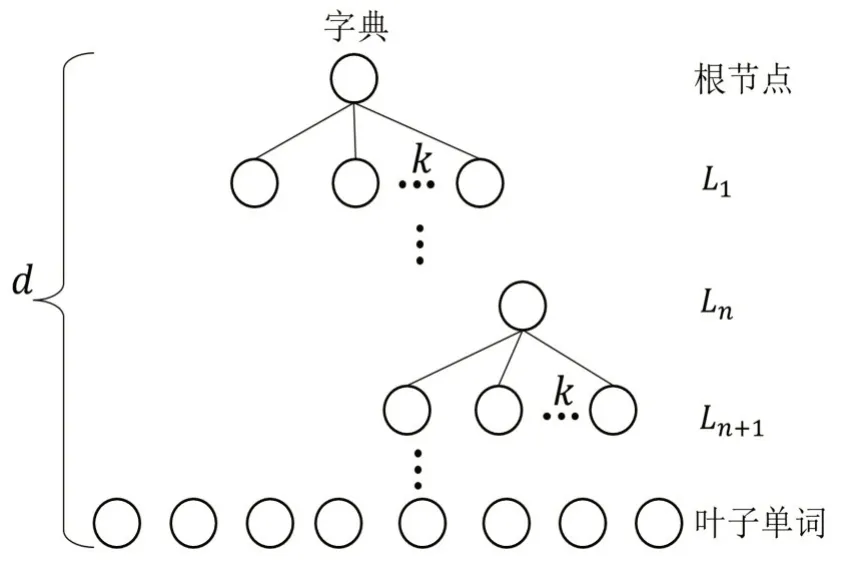
图3 词袋向量计算原理图

对于当前帧中的每一个ORB 特征点的描述子，首先从离线字典中找到自己的位置，然后从根节点开始，计算ORB 特征点的描述子与根节点下每个节点的描述子的汉明距离，再将汉明距离最小的节点作为自己所在的节点，依次类推，搜索到叶子单词节点。当搜索完当前帧所有ORB 特征点的描述子后，就得到了当前帧的词袋向量。

得到当前帧的词袋向量之后，通过词袋向量进行帧间特征匹配。从图3中的第Ln层开始一直到叶子层，使用汉明距离来度量当前帧和参考帧之间属于同一节点下ORB 特征点的描述子。最后将描述子汉明距离最小且明显低于次小的点对作为成功匹配点对。这样做缩小了特征点的匹配范围，与传统的暴力匹配相比大大地提升了系统的匹配效率。

2.4 列文伯格-马夸尔特算法最小化重投影像素点灰度误差

系统在单目（Mono）模式、RGB-D 模式或者双目（Stereo）模式下，针对静态场景，运用最小化重投影像素点灰度误差方法来提高系统的定位精度。图4所示为该方法的原理图。

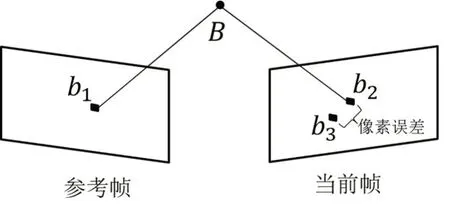
图4 最小化重投影像素点灰度误差原理图

图4 中，b1和b2为通过帧间特征匹配得到的匹配点对，它们对应的像素点坐标分别为u1和u2。B为b1和b2对应的空间路标点，它在世界坐标系下对应的四维齐次坐标为BW。根据当前帧相机位姿初值Tcw，B在当前帧的投影点为b3。相机通过标定得到内参矩阵K：

根据内参矩阵K，b3的像素点坐标u3可通过式（2）推算：

式中：z为B的深度值，Tcw为世界坐标系到当前帧坐标系的变换矩阵。

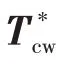
2.5 列文伯格-马夸尔特算法最小化深度误差

系统在RGB-D 模式或者双目模式（Stereo）下，针对动态场景，运用最小化深度误差方法来提高系统的定位精度。图5所示为该方法的原理图。

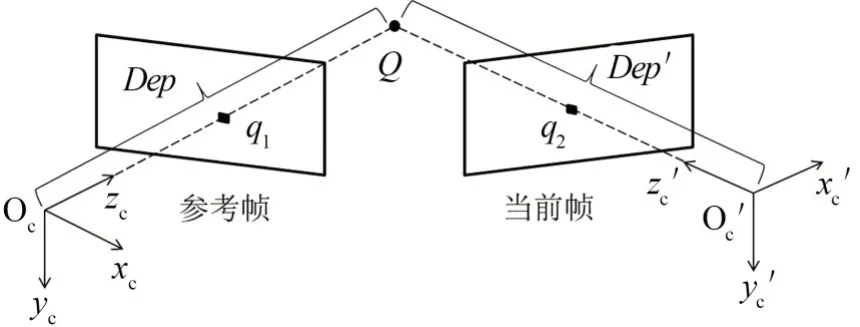
图5 最小化深度误差原理图

图5 中，q1和q2为通过帧间特征匹配得到的匹配点对；Q为q1和q2对应的空间路标点，它在世界坐标系下对应的四维齐次坐标为Qw。由于参考帧的相机位姿Trw在优化当前帧位姿前已经优化获得，所以可以根据式（6）推算出空间路标点Q在参考帧坐标系下的深度Dep：

式中：Qr表示在参考帧坐标系下Q的四维齐次坐标，Qr第三维的值就是深度Dep，Trw表示世界坐标系到参考帧坐标系的变换矩阵。

在当前帧坐标系下，q2的深度值Dep′可通过RGB-D 相机或双目相机恢复。由于Dep与Dep′的维度为一，无法进行矩阵运算，所以将Dep与Dep′扩展成四维齐次坐标（Dep与Dep′）。其中，第一维和第二维的值为零，第三维的值就是深度值，最后一维的值为一。接着根据当前帧相机位姿初值Tcw，利用式（7）～（8）将Dep′从当前帧坐标系转换到参考帧坐标系：

式中：Trc为当前帧坐标系到参考帧坐标系的变换矩阵。Dep″是Dep′从当前帧坐标系转换到参考帧坐标系的四维齐次坐标。

由于当前帧相机位姿初值精度不高，导致Dep′转换到参考帧坐标系下的值Dep″与Dep存在误差，因此，可利用列文伯格-马夸尔特算法最小化误差目标函数，得到Trc的最优值，即：

2.6 像素点灰度误差、深度误差与像素点坐标误差的联合优化

为了更好地提高视觉里程计系统的定位精度，引入了ORB-SLAM2 中所运用的PnP 最小化重投影误差方法[17]，并将它与最小化重投影像素点灰度误差及最小化深度误差方法相结合，进行多重位姿优化。因为最小化重投影误差实质上就是最小化像素点坐标误差，且本文提出了最小化重投影像素点灰度误差，所以为了更好地将两者区分开来，把最小化重投影误差重新命名为最小化重投影像素点坐标误差。运用列文伯格-马夸尔特算法，最小化重投影像素点坐标误差由式（12）描述：

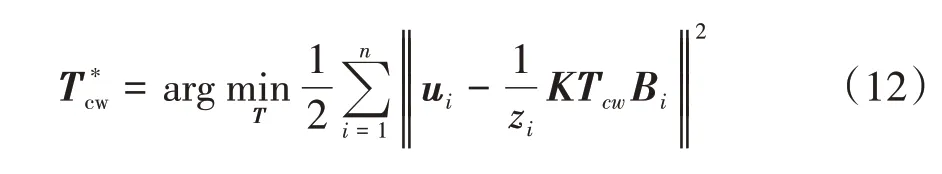
列文伯格-马夸尔特算法所需的雅克比矩阵J可由式（13）描述：

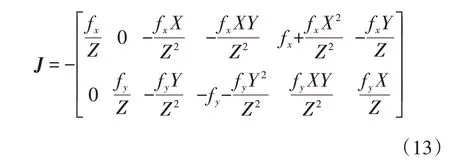
针对静态场景，首先利用g2o 库对匹配好的点对进行最小化重投影像素点坐标误差，进而估计相机位姿，将g2o 的点设置为相机位姿、边设置为空间路标点，求解器设置为列文伯格-马夸尔特求解器，而最小化重投影像素点坐标误差的相机位姿初值由ORB-SLAM2 中的参考关键帧模型和恒速模型[17]给出。因为有误匹配点对的存在，所以单靠最小化重投影像素点坐标误差得到的相机位姿往往不够准确。为了提高相机位姿估计精度，在得到初步估计的相机位姿的同时，利用g2o 将误匹配点对剔除，然后把初步估计的相机位姿作为初值，再用最小化重投影像素点灰度误差得到最终估计相机位姿。

由于像素点坐标误差的自由度为2，所以选取显著水平在5%以下的卡方检验值5.99 作为阈值。当g2o 边的误差EdgeError超过5.99 时，就将其视为误匹配点对并剔除。剔除误匹配点对策略如式（14）所示：

针对动态场景，和静态场景相似，利用g2o 库，先对匹配好的点对进行最小化深度误差处理以估计相机位姿，再将g2o 的点设置为相机位姿、边设置为空间路标点，求解器设置为列文伯格-马夸尔特求解器，而最小化深度误差的相机位姿初值由ORB-SLAM2 中的参考关键帧模型和恒速模型[17]给出。由于在动态场景中，动态物体上的空间路标点在相机坐标系下的深度值是不会严格根据相机位姿的改变而改变的，所以它们的匹配点对的深度值在同一坐标系下的差异往往会比较大。根据这一推断，在通过最小化深度误差得到相机位姿的同时，将深度误差较大的匹配点对视为动态匹配点对，并将其剔除。

由于深度误差的自由度为1，所以选取显著水平在5%下的卡方检验值3.84 作为阈值。当g2o 边的误差EdgeError超过3.84时，就将其视为动态点并剔除。剔除策略如式（15）所示：

因为最小化深度误差得到的初步估计的相机位姿受动态点的影响，估计值精度不高，所以在剔除了动态点之后，为了进一步提高相机位姿估计精度，继续将初步估计的位姿作为初值，利用最小化重投影像素点坐标误差，得到最终估计相机位姿。

3 实验与分析

本文的实验主要包括静态与动态场景下本文所提方法的定位精度分析。实验配置：PC的CPU型号为Intel i7-5557U，主频为3.10 GHz，运行内存为8 GB；PC运行的系统为Ubuntu 16.04；实验评估工具为EVO。

3.1 静态场景下本文所提方法的定位精度分析

针对静态场景，本文选取了TUM 数据集和EuRoC 数据集里一共8 个不同的图像序列，分别针对单目（Mono）、RGB-D 和 双 目（Stereo）模 式与ORB-SLAM2算法[17]进行轨迹绝对误差对比实验。

表1 列举了所选取的TUM 数据集序列在单目（Mono）与RGB-D 模式下本文所提方法估计轨迹、ORB-SLAM2 算法[17]估计轨迹与真实轨迹之间的绝对误差对比分析结果。图6 所示为TUM 数据集上本文所提方法和ORB-SLAM2 算法的估计轨迹与真实轨迹之间的对比图。

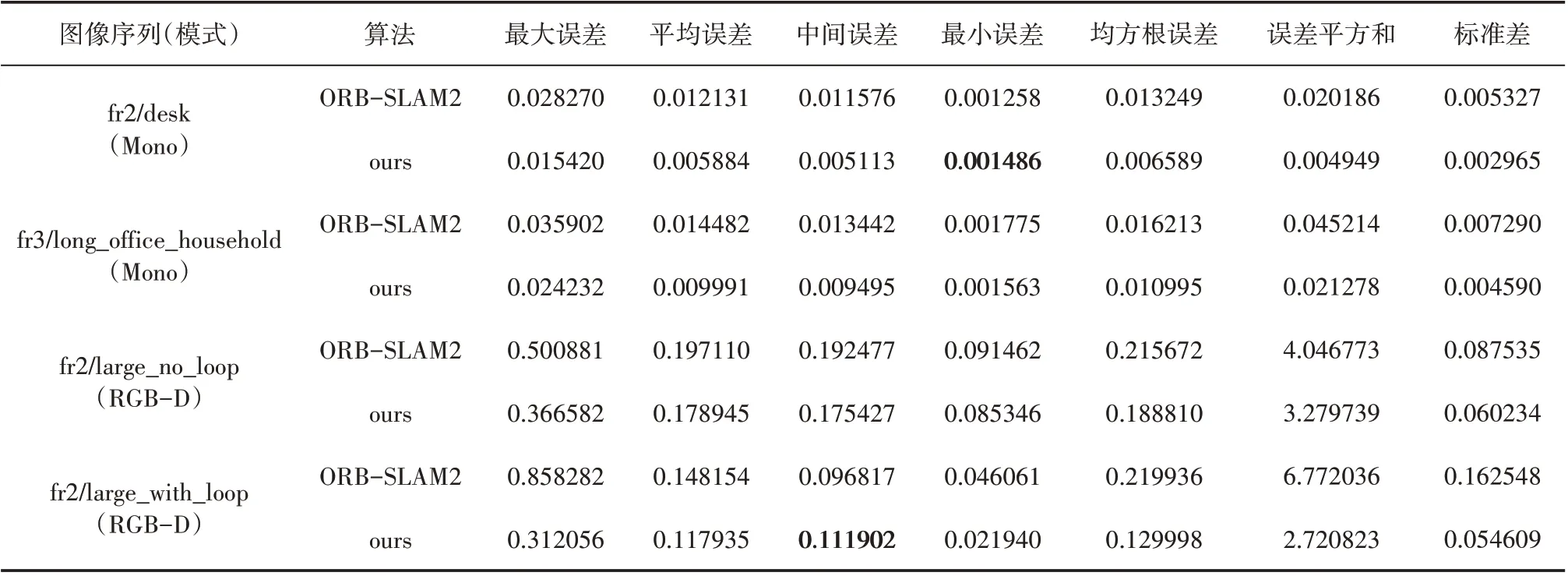
表1 TUM数据集上本文所提方法与ORB-SLAM2算法所估计轨迹的绝对误差比较 m

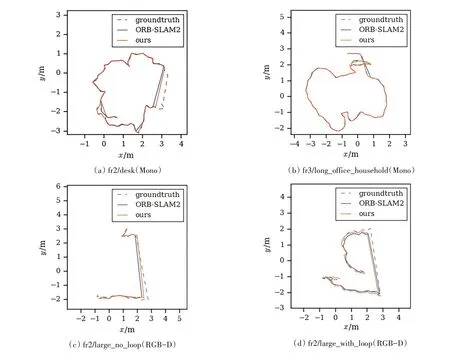
图6 TUM数据集上本文所提方法与ORB-SLAM2算法所估计轨迹对比图

表2列举了所选取的EuRoC 数据集序列在单目（Mono）与双目（Stereo）模式下本文所提方法估计轨迹、ORB-SLAM2算法[17]估计轨迹与真实轨迹之间的绝对误差对比分析结果。图7所示为EuRoC数据集上本文所提方法和ORB-SLAM2 算法的估计轨迹与真实轨迹之间的对比图。

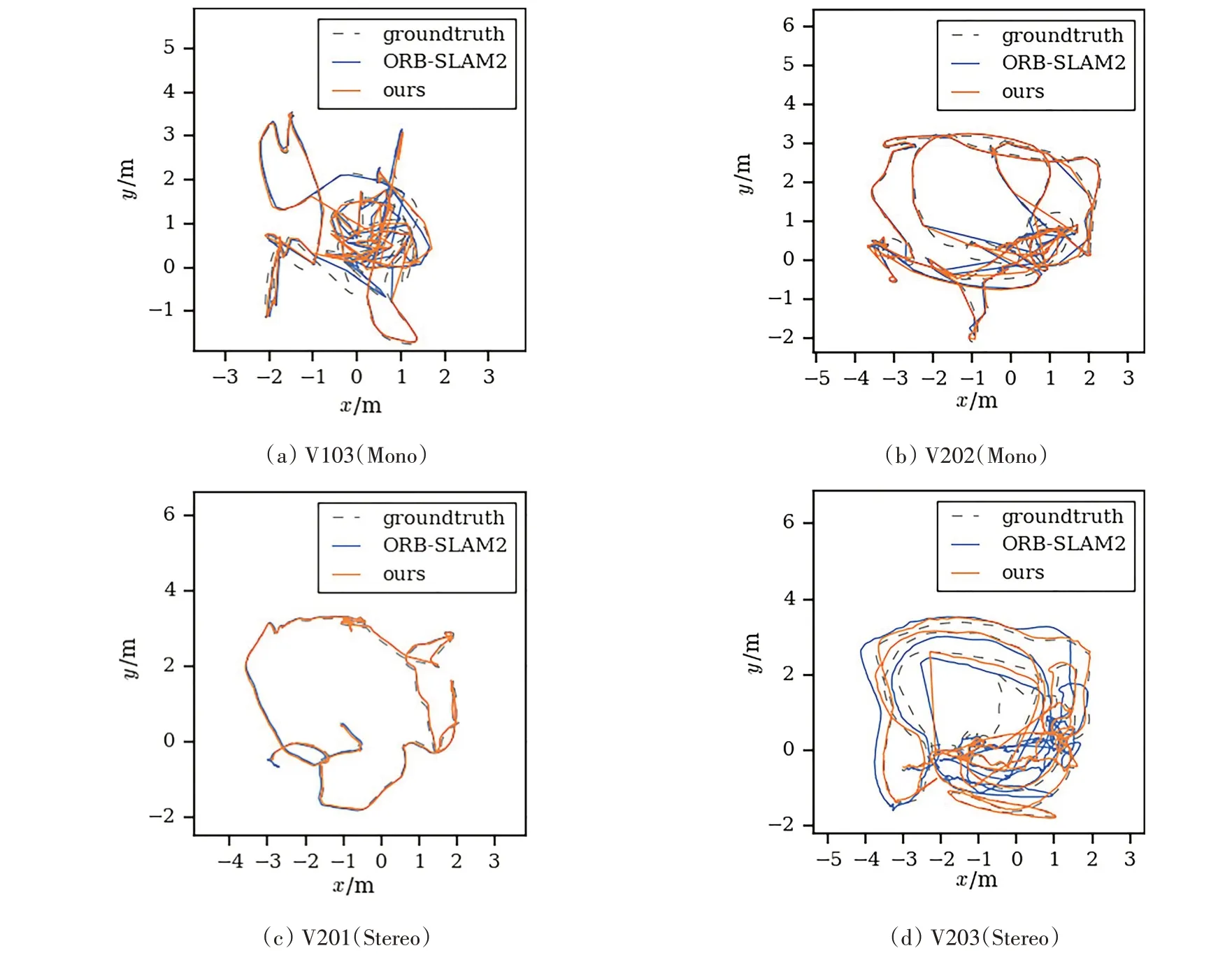
图7 EuRoC数据集上本文所提方法与ORB-SLAM2算法所估计轨迹对比图

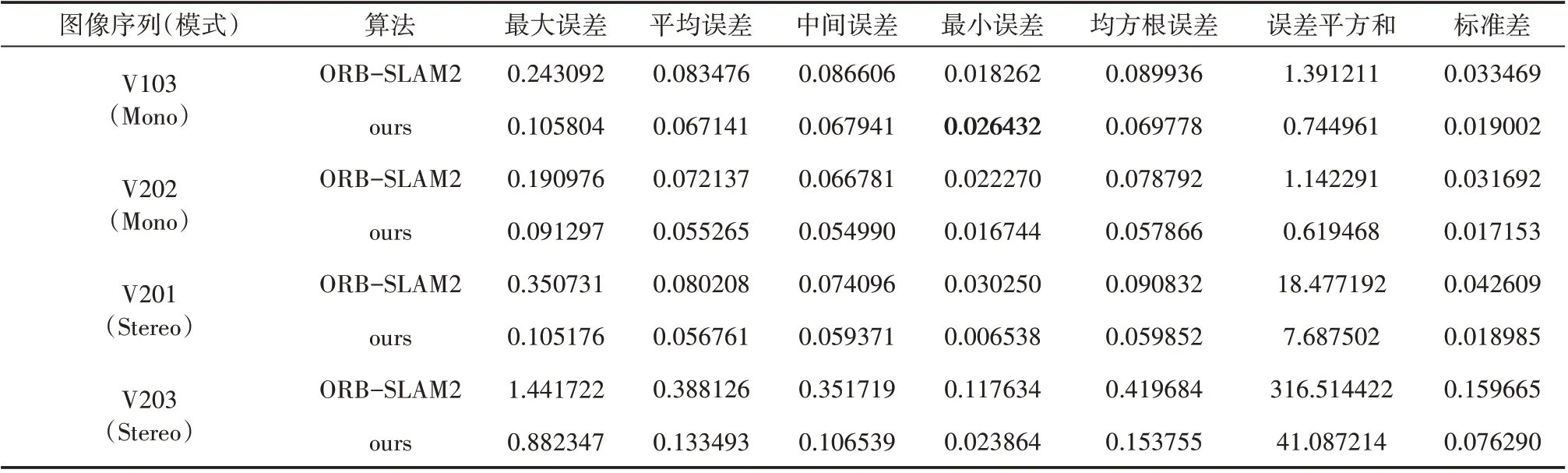
表2 EuRoC数据集上本文所提方法与ORB-SLAM2算法所估计轨迹的绝对误差比较 m

由上面的实验结果可知：不管是在相机轨迹较为简单的TUM 数据集上，还是在较为复杂的EuRoC数据集上，本文所提方法在单目（Mono）、RGB-D 和双目（Stereo）模式下与真实轨迹的最大误差、平均误差、均方根误差、误差平方和及标准差都明显低于ORB-SLAM2 算法；而中间误差除表1 中标黑的一个、最小误差除表1 中标黑的一个及表2 中标黑的一个之外，也都明显低于ORB-SLAM2 算法。这说明本文所提方法在静态场景下可以有效地增强ORB-SLAM2算法的定位精度，从而提高系统性能。

3.2 动态场景下本文所提方法的定位精度分析

针对动态场景，本文选取了TUM 数据集和KITTI数据集里一共4个不同的图像序列，分别针对RGB-D 和双目（Stereo）模式与ORB-SLAM2 算法[17]进行轨迹绝对误差对比实验。表3列举了所选取的TUM 数据集和KITTI 数据集分别针对RGB-D 与双目（Stereo）模式下本文所提方法估计轨迹、ORBSLAM2 算法[17]估计轨迹与真实轨迹之间的绝对误差对比分析结果。图8 所示为TUM 与KITTI 数据集上本文所提方法和ORB-SLAM2 算法的估计轨迹与真实轨迹之间的对比图。

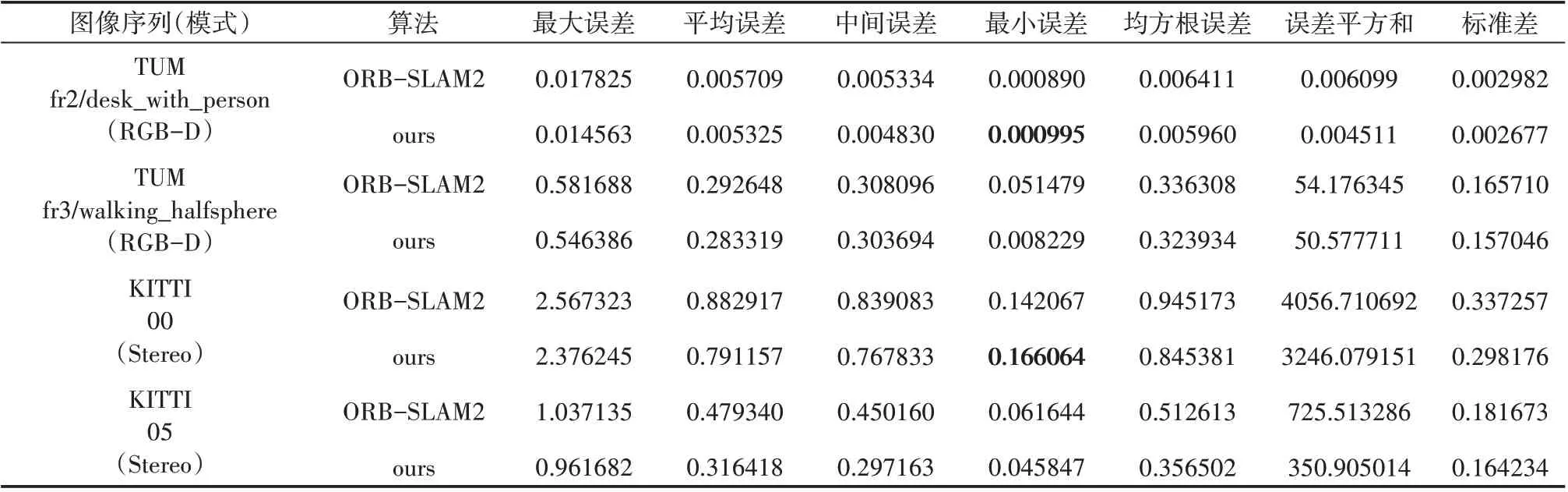
表3 TUM与KITTI数据集上本文所提方法与ORB-SLAM2算法所估计轨迹的绝对误差比较 m

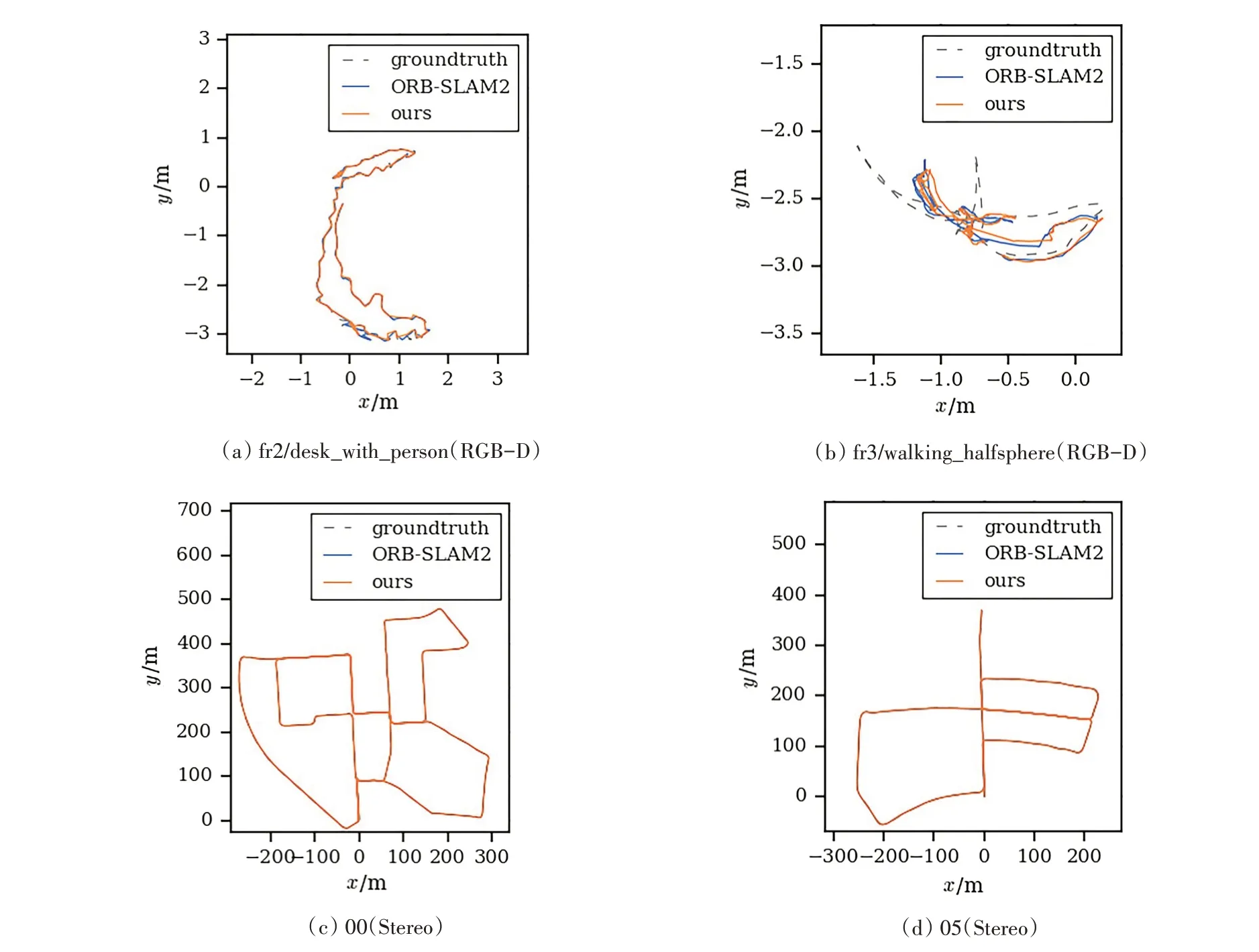
图8 TUM与KITTI数据集上本文所提方法与ORB-SLAM2算法所估计轨迹对比图

TUM 数据集里面的动态场景多为室内行人，而KITTI 数据集里面的动态场景多为室外行人与过往车辆。由上面的实验结果可知：无论是针对TUM 数据集还是KITTI 数据集里的动态场景，本文所提方法在RGB-D 与双目（Stereo）模式下与真实轨迹的最大误差、平均误差、中间误差、均方根误差、误差平方和及标准差都明显低于ORB-SLAM2 算法；而最小误差除表3 中标黑的两个之外，也都低于ORBSLAM2 算法。这说明本文所提方法在动态场景下对提高系统的定位精度，改善系统性能有一定效果。

4 结束语

针对静态场景和动态场景，分别提出了最小化重投影像素点灰度误差与最小化深度误差方法。在静态/动态场景中，首先利用最小化重投影像素点坐标误差/最小化深度误差得到初步估计的相机位姿，同时剔除误差较大的误匹配点对。然后将初步估计的相机位姿作为初值，利用最小化重投影像素点灰度误差/最小化重投影像素点坐标误差得到最终估计相机位姿。实验结果表明，将此方法运用在ORB-SLAM2算法中，能够有效提高ORB-SLAM2算法的定位精度及系统性能。