基于循环相关的相干信源角度估计

金芳晓，孙元峰

(1． 中国电子科技集团公司第三十八研究所，合肥 230088；2． 汽车智能网联与主动安全技术国家地方联合工程研究中心，合肥 230088)

0 引 言

研究表明，许多人造和自然界中的信号都是由周期现象产生，虽然这些信号不是时间的周期过程，但其统计特征随时间呈现周期性变化，被称为广义循环平稳过程[1]，已广泛用于通信、雷达、无线电等领域。基于信号循环平稳特性的选择性测向算法，如Cyclic MUSIC、SC-SSF、Cyclic ESPRIT等，由于其能够提高信号检测能力，在雷达和通信系统中得到了广泛关注[2-4]。此外，循环平稳类DOA估计算法只要求在特定感兴趣循环频率下的信源数少于阵元数，因此，即使总信源数大于阵元数，算法也能正确估计出期待信号角度。也就是说，基于此类DOA估计算法可以提高阵列自由度，已成为阵列信号处理的研究热点之一。

建立在子空间上的MUSIC、ESPRIT等DOA估计算法不适用于存在同频干扰的情况，此外还有一个很大的局限性：在实际环境中多径效应或人为设置干扰等导致的一种相干环境下的DOA估计问题。对于传统超分辨算法，当接收信号存在相干性时，子空间特征值分解后无法得到与信号源对应的特征向量。这也是超分辨的重点研究对象之一。为了准确分辨相干信号，主要采用子空间拟合法、空间平滑法、奇异值分解法、矩阵分解法等几种解决方法。改进的MUSIC算法[5-6]采用数学方法对数据协方差矩阵做变换处理，使其相关协方差矩阵秩个数与相干信号源个数相等，进而分辨相干信号的来波方向。为了进一步提高抗噪性，文献[7]、[8]基于压缩感知理论，提出了几种稀疏重构的DOA估计算法，利用空域的稀疏特性重构空间谱，不受信号相干性的影响。这类算法普遍存在初始参数难以设置和计算量较大的问题，一定程度上限制了其应用。

针对同频干扰和相干信号同时存在的复杂环境，本文利用信号的循环平稳特性解决相干信号DOA估计问题，提出一种基于循环相关的相干信源角度估计算法，并通过仿真实验验证了其有效性。

1 信号模型

1.1 循环相关函数

循环平稳过程是一类特殊的非平稳随机过程，其统计函数随时间呈现周期变化，广泛应用于雷达、无线电、遥感等领域。依据期望信号和同频干扰往往具有不同的循环频率这一特点，实现对干扰信号的抑制。

对于一个具有二阶周期特性的非平稳信号x(t)，其时变自相关函数可表示为[9]

为避免随机性，令N趋于无穷，可以得到

(2)

进一步将rx(t,τ)展开成傅里叶级数的形式：

(3)

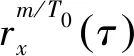
(4)

将式(2)代入式(4)，有

=〈x(t+τ/2)x*(t-τ/2)e-j2πmt/T0〉t

(5)

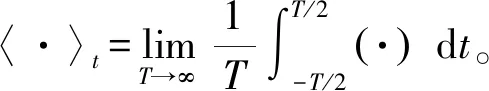
设信号x(t)包含多个互不可约的周期信号，则式(3)和式(5)可分别表示为

(6)

=〈x(t+τ/2)x*(t-τ/2)e-j2πεt〉t

(7)

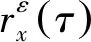
1.2 阵列模型

假设K个远场窄带期待信号和干扰信号xk(t),k∈{1,…,K}，入射到均匀线阵上，其中Kε≤K个信号为期待信号，具有相同的循环频率ε，且期待信号间存在相干性。均匀线阵由M个阵元组成，相邻阵元间距D，则在t时刻阵列接收数据表示为

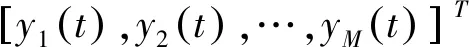
(8)

(9)

式中，υmk为第k个信号到达第m个阵元相对于参考阵元的时延，且υmk=(m-1)Dsinθk/c，θk为第k个信号的方向角，c为波速；nm(t)为第m个阵元在t时刻的噪声，该噪声为独立源，且与信号统计独立。

1.3 相干信源的信号模型

传统的超分辨算法仅能估计非相关信号源，且随信号源间相关性(或相关系数)的增加，其性能逐渐恶化，直至失效。在实际应用环境中，很可能存在多径反射或人为设置导致的相干信号。对于两个平稳信号s1(t)和s2(t)，其相关系数可以表示为

(10)

对于不同信号的关系可以做出如下定义：

(11)

因此，当两个信号相干时，两者的区别仅仅是差一个常复数。

2 相干信源角度估计算法研究

2.1 线性预测模型

从式(9)可以看出，第M个阵元的接收信号可看作是由其他M-1个阵元接收信号的相移组合而成，即

(12)

式中，βi=(i-1)Dsinθk/c；eM(t)为预测误差。

基于式(12)求取yM(t)的循环相关函数，可得LP模型如下：

(13)

进一步，可将式(13)表示为向量形式：

(14)

式中，

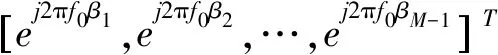
在有限快拍数下，假设阵列接收信号y(t)的离散表示形式为y(n)，且阵列信号的快拍数为N，可以得到各阵元的离散循环相关函数：

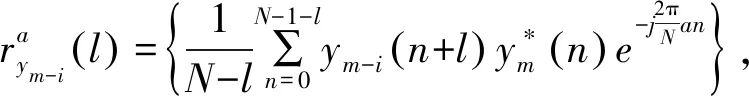
m=1,…,M

(15)

式中，a=(ε/fs)N∈[0,fs]为数字循环频率；e-jπ/Nal为校正因子；l=0,1,…,L-1为数字时延，且L≤N。

令l=0,1,…,L-1，从而得到信号模型的离散循环相关熵矩阵：

r=Φq

(16)

式中，

2.2 相干信号角度估计

由于矩阵q中包含角度信息，问题便转为对矩阵q的估计问题。为此，求解式(15)矩阵Φ的协方差矩阵：

Σφ=ΦHΦ

(17)

由于接收到的不同方向阵列信号存在相干性，相干信号导致协方差矩阵的秩亏缺。为此，利用Toeplitz矩阵的性质[10]修正矩阵Σφ，可以得到Σφ的Toeplitz协方差矩阵估计值：

Σ=Σφ+IvΣφIv

(18)

再对该无偏估计Σ进行特征值分解，有

Σ=UΛUH

(19)

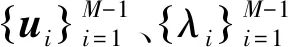
由于期待信号个数是Kε，所以取前Kε个特征值对式(16)中的矩阵q进行求解：

(20)

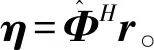
最终，所要求的期望信源的DOA估计值便为下面预测多项式(21)所对应的谱峰位置：

(21)

式中，w=ej2πεDsinθ/c。

算法的整体步骤如下：

步骤2：根据式(17)计算Φ的协方差矩阵Σφ；

步骤3：根据式(18)计算Σφ无偏估计矩阵Σ；

步骤5：根据式(20)计算目标矩阵q；

步骤6：利用式(21)求解空间谱P(θ)，进而采用谱峰搜索的方式求得期望信号DOA估计值。

3 仿 真

计算机仿真实验采用10阵元均匀线阵，阵元间距为c/2ε，ε为入射信号的循环频率。设定存在3个期待信号和1个同频干扰，其中3个期待信号中有2个为远场BPSK相干信号，且与第3个信号不相干；2个相干信号入射角度分别为19°和52°，另一个不相干信号入射角度为32°。阵列中还存在同载频的AM干扰信号，其入射角为40°。信号的采样频率为fs=500 MHz，快拍数N=500，信噪比SNR=0 dB。

实验中采用L1-SVD和SC-SSF两种算法与本文算法进行对比，以检测DOA估计的性能：L1-SVD算法采用压缩感知重构思想对角度进行估计，对各个方向的入射信号进行稀疏重构，可较好地解决相干问题，对相干信号进行DOA估计，但该算法同样对同频干扰的影响也较大；SC-SSF对比算法采用循环频率构建线性模型进行角度估计，可以抵抗同频干扰的影响，但是不具有解相干的能力。

在上述同频干扰和相干信号共存的条件下，实验仿真结果如图1所示。可以看出，L1-SVD算法虽然很好地解决了相干信号问题，但是受同频干扰影响，在干扰的入射方向旁瓣抬高；本文算法和SC-SSF算法利用两个期望信号与干扰源信号具有不同的循环频率这一循环平稳特性，较好地抑制了同频干扰信号，实现了对期待信号来波方向的估计； SC-SSF算法由于不具有解相干，无法估计相干信号的角度。综合来看，本文算法较好地抑制了同频干扰，且受相干信号影响较小，很好地估计出了3个期待信号的来波方向。

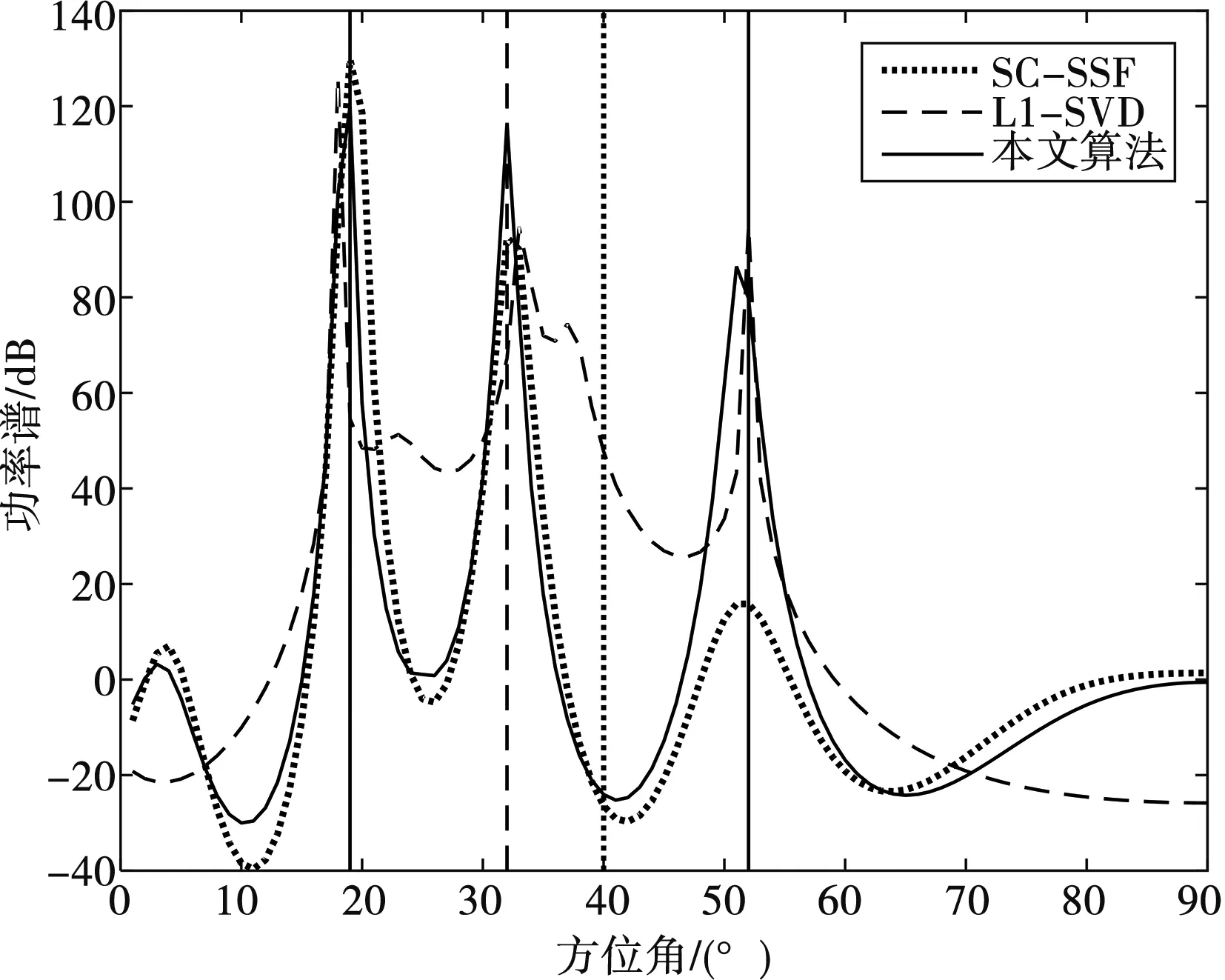
图1 3种算法DOA估计空间谱对比图

DOA估计中的信噪比是影响算法性能的重要因素。为此，本文进一步就信噪比对DOA估计的影响做了仿真实验，信噪比-10～10 dB，其他条件不变。由于在上述仿真条件下，SC-SSF算法无法估计出具有相干性的2个信号，因此在信噪比实验中，仅对比本文算法和L1-SVD算法的估计均方根误差随信噪比变化情况，独立实验100次，仿真结果如图2所示。可以看出，L1-SVD算法受同频干扰的影响，在低信噪比下DOA估计误差较大。随着信噪比的提高，2种算法的估计误差均在减小，且在信噪比大于5 dB后，算法性能都趋于稳定。而且，L1-SVD算法由于采用稀疏重构，在高信噪比条件下估计误差要略小于本文算法。

图2 均方误差随信噪比变化

4 结束语

为抑制同频干扰，本文基于阵列接收通道间的线性关系，构建信号接收循环相关矩阵模型，采用最小二乘法对参数进行估计。同时，将阵列接收循环相关协方差矩阵的无偏估计纳入所提LP模型中，解决了循环平稳相干信号的高分辨角度估计问题。仿真实验表明，在受同频信号干扰且信噪比较低的情况下，本文算法性能更好，且受相干信号的影响较小。