飞翼无人机多形翼尖P频段RCS特性及影响分析*

王若尘，杨延平，张国鑫，王 波，马晓平

(1.中国科学院工程热物理研究所，北京 100190；2.中国科学院大学，北京 100049)

0 引 言

电子探测技术和导弹技术的迅猛发展对军用飞机构成了很大的威胁，为了提高作战飞机的生存能力，隐身化已经成为了先进飞行器发展的必然特征之一[1]。自20世纪50年代美国提出飞机隐身性问题以来，隐身技术在飞机外形综合设计中受到越来越多的重视，大大提高了飞机的生存能力。国外著名的隐身作战飞机包括美国的F-117A、B-2、X-47B等，俄罗斯的Su-47、T-50等[2-3]。P频段是雷达探测的重要频段，相比于其他频段如C频段、S频段、X频段等，P频段雷达具有天然的反隐身优势——绝大部分隐身目标都处于P频段雷达的谐振区且涂抹吸波材料隐身的方式对P频段不具备工程可行性[4]。因此，掌握P频段电磁散射特性对发展隐身无人机至关重要。

飞翼布局飞行器由于构型特性在隐身方面有着天然优势。飞翼布局将机身与机翼高度融合，并取消了尾翼，因此具有良好的雷达隐身性能，成为了新一代战机的热门设计方向[5]。对于飞翼、菱形翼等低雷达散射截面(Radar Cross Section,RCS)隐身飞行器而言，除了三大强散射源(机载雷达舱、座舱及进气道)之外，飞机表面缝隙、台阶、对缝以及翼尖等弱散射源也是必须考虑的隐身设计难点。研究表明，弱散射源可导致飞机前向RCS增加1 m2，对隐身性能有较大的影响[6]。为了进一步提升飞行器隐身性能，值得对弱散射源进行深入研究。

由于弱散射源的研究背景相当敏感，国外相关的文献资料较少。文献[7]和文献[8]提出了两种RCS的检测方法，指出将环境与目标信号进行分离有利于弱散射源的精确测量，但这些方法很难应用到飞机弱散射源的测量中。Hu等[9]利用微波成像算法与光谱变换的方式提取出弱散射源的二维反射率分布，以提高其计算精度，并进行了样机试验设计，验证了该方法能够更准确地获得弱散射源的RCS特性。而国内针对飞行器弱散射源的研究主要集中在锯齿、表面缝隙、台阶、边缘、机身侧棱等区域[6,10-14]。桑建华等[6]研究了飞行器表面缝隙、台阶、对缝等弱散射源对前向RCS的影响，指出减小缝隙宽度和台阶高度，采用锯齿缝隙代替直缝隙，可以有效控制隐身飞行器表面的电磁缺陷。刘战合等[10]基于多层快速多极子方法(Multi-level Fast Multiple Algorithm,MLFMA)对飞行器锯齿边板的散射特性进行研究，总结了锯齿边板相对于直边板在不同角域内的RCS减缩特性以及RCS减缩与入射频率变化之间的关系。黄沛霖等[11]针对飞行器表面缝隙开展RCS测试，研究了RCS随单缝隙宽度与多缝隙间距之间的变化规律及其极化特性。张维仁等[12]基于MLFMA对机翼后缘的电磁散射特性展开分析，讨论了后缘半径和展长参数对机翼后缘RCS的影响，并利用吸波材料减缩后缘产生的行波散射。张扬等[13]以棱边长度、棱边尖劈角和棱边厚度作为关键参数，研究了机身侧棱对隐身飞行器电磁散射特性的影响。目前，针对翼尖的电磁散射特性研究较少，而翼尖的尖点绕射如果不加以控制，足以破坏飞行器的隐身性能[14]。基于此，徐顶国等[15]设计了直切和斜切的不同翼尖外形方案，对不同频段、不同方位角翼尖尖点散射特性展开分析，得到翼尖的最优方案。但是，作者仅对翼尖部分单独进行分析，并未在全尺寸飞机上进行研究，因此不能很准确地反应翼尖形状对整机电磁散射特性的影响。为更直观地反应翼尖形状的影响，需进一步将翼尖置于全尺寸飞机上进行对比分析。

基于上述问题，本文考虑构建多形翼尖的方法，针对典型飞翼无人机开展数值仿真计算，比较并分析不同翼尖形状对飞翼无人机P频段H-H极化RCS的影响，进一步分析不同切割位置对整机RCS的影响，旨在为翼尖RCS特性研究提供一定的参考。

1 飞翼无人机及多形翼尖建模

本文所采用的模型为双后掠飞翼布局无人机，如图1所示，其主要设计参数见表1。

图1 飞翼无人机模型

表1 飞翼无人机基本参数

将图1中虚线以外的部分定义为原始翼尖。为了探究不同翼尖外形对飞翼P频段电磁散射特性的影响，对原始翼尖采用了直切与斜切的处理方式，并对剪切面进行了低RCS处理，得到如图2所示的三种不同翼尖形状。

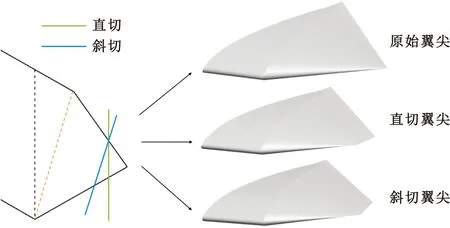
图2 不同翼尖形状示意图

2 高精度MLFMA算法设计

2.1 计算方法分析

电磁散射特性的计算方法主要包括高频近似法与精确算法。常用的高频近似方法包括物理光学法、几何光学法、一致性绕射理论等，精确算法主要包括矩量法(Method of Moment,MoM)与MLFMA等，其优缺点见表2。

表2 常见电磁散射计算方法优缺点

MLFMA的原理是通过对远场、近场的分别处理加速迭代过程中矩阵与向量的相乘，从而达到快速计算的目的。其中，对于附近区强耦合量采用直接计算，对于非附近区耦合量采用MLFMA实现，其特点是逐层聚合、逐层转移、逐层配置与嵌套递推。

由于本文分析的雷达频段为P频段，属于低频频段，高频近似方法不再适用。而相比于MoM，MLFMA具有相似的精度且计算速度快，所需内存小，非常适合计算电大尺寸问题，被广泛运用在飞行器RCS仿真计算中，因此本文考虑采用MLFMA进行仿真分析。

2.2 精度验证

精度验证是仿真分析保证精确度的基础。Metallic Cone Sphere With Gap是验证P频段电磁散射特性的标准模型，其长度约为0.689 m(27.127 in,1 in=25.5 mm)，如图3所示。文献[16]采用了MLFMA对标准模型Metallic Cone Sphere With Gap 0°～180°方位角范围内的电磁散射特性进行仿真计算，入射波频率为869 MHz，网格采用三角形网格，极化方式采用H-H极化与V-V极化。将文献[16]的MLFMA计算结果与文献[17]中的实验结果与数值结果(MoM)进行对比，得到如图4所示的仿真结果与实验数据对比图。

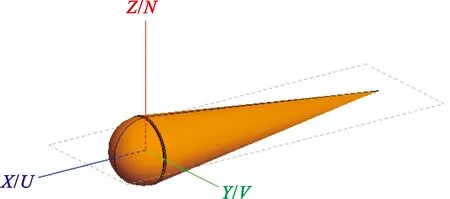
图3 Metallic Cone Sphere With Gap模型

(a)869 MHz下 H-H极化RCS

结合图4可知，在大部分方向上，MLFMA方法与实验数据吻合很好，而吻合不好的部分，经与文献[17]中的数值结果进行比较，相差很小，从而验证了MLFMA在P频段的精确性。

3 多形翼尖RCS仿真及全机特性分析

3.1 不同翼尖方案对整机RCS影响对比分析

为探究不同翼尖方案对整机RCS特性的影响，利用MLFMA对三种不同翼尖的飞翼无人机进行仿真计算，计算参数设置见表3。

表3 不同翼尖方案仿真的计算参数设置

分别计算入射波频率为300 MHz时三种飞翼无人机在0°～180°方位角，0°、5°、10°和15°迎角下的H-H极化RCS，计算网格采用三角形网格，网格的边长设定为入射波长的1/8，计算类型为单站RCS，得到图5所示的飞翼无人机RCS随迎角变化图。

(a)0°迎角下H-H极化RCS

从图5中可以看出，在不同的迎角下，三种不同翼尖的飞翼无人机整体趋势相近，在方位角为30°和55°附近出现波峰，分别对应飞翼无人机外翼与内翼。此外，在方位角0°～30°范围内三种飞翼的RCS有着较为显著的差距。为探究三种翼尖对整机前向RCS的影响，以方位角0°～30°范围内RCS的平均值作为衡量飞翼前向RCS的指标，其计算方式如下：

(1)

(2)

表4 三种飞翼H-H极化下前向RCS平均值

结合表4所示的三种不同翼尖飞翼无人机在不同迎角、H-H极化条件下前向RCS平均值，可以得到以下结论：

(1) 当迎角为0°和5°时，三种飞翼前向RCS平均值十分接近，而当迎角大于5°时，随着迎角的增大，前向RCS平均值不断增大；

(2)相比于原始翼尖，直切翼尖与斜切翼尖都能在一定程度上减小前向RCS平均值；

(3)直切翼尖在降低前向RCS方面具有最显著的效果。

3.2 不同切割位置对整机RCS影响对比分析

由3.1节可知，直切翼尖相对于原始翼尖和斜切翼尖具有更优的前向RCS特性。为了进一步探究直切翼尖方案下直切位置对前向RCS的影响，选取了六个不同的直切位置进行对比分析。六种直切翼尖方案如图6所示，其中红色实线为直切参考线，分别选取参考线由外向内5%、10%、15%、20%、25%和30%位置进行直切，并对切面进行低RCS处理，得到六种不同直切翼尖的飞翼无人机。

图6 六种直切翼尖方案示意图

利用MLFMA对六种不同直切翼尖的飞翼无人机进行仿真计算，选取的计算状态如表5所示。

表5 不同直切位置仿真的计算参数设置

计算网格同样采用三角形网格，网格的边长设定为入射波长的1/8，计算类型为单站RCS，得到图7所示的不同直切翼尖H-H极化与V-V极化飞翼RCS对比图。

(a)0°迎角下六种直切翼尖飞翼H-H极化RCS

(b)0°迎角下六种直切翼尖飞翼V-V极化RCS

结合图7可知，H-H极化下六种不同直切翼尖飞翼无人机在方位角0°～30°范围内的RCS差距较为明显，而在V-V极化下趋势基本一致。为了进一步探究不同直切方案的影响，对H-H极化与V-V极化下方位角0°～30°范围内平均RCS进行计算，所得结果如表6所示。

表6 六种直切翼尖飞翼在0°迎角下前向RCS平均值

结合表6分析，针对不同切割位置对整机前向RCS特性的影响，可以得到以下结论：

(1)H-H极化对整机RCS特性的影响大于V-V极化，具体表现为H-H极化下前向RCS平均值均小于V-V极化，同一状态两者的差距约为8 dBm2；

(2)不同切割位置对H-H极化的影响大于V-V极化，H-H极化下六种直切翼尖飞翼前向RCS平均值的方差大于H-H极化；

(3) H-H极化下，前向RCS平均值随直切位置的不断向内呈现先减小后增大的趋势：直切位置为参考线15%处RCS平均值最小，而直切位置为参考线5%处RCS平均值最大，两者相差0.53 dBm2；

(4)V-V极化下，前向RCS平均值较为接近，直切位置为参考线20%处RCS平均值最小，而直切位置为参考线30%处RCS平均值最大，两者相差0.13 dBm2；

(5)以对整机RCS影响较大的H-H极化特性作为衡量依据，直切位置为参考线15%处的直切方案具有最好的前向RCS特性，且相比于原始翼尖，H-H极化下前向RCS平均值降低了0.78 dBm2，说明该最优方案对前向RCS的贡献有较显著的降低。

综上所述，直切位置为参考线15%处的直切翼尖方案具有最优的前向RCS特性，且相较于原始翼尖RCS性能有所提高。

4 结束语

本文利用高精度MLFMA方法，设计了直切与斜切两种不同的翼尖方案，分析了不同翼尖方案下飞翼无人机P频段RCS随迎角的变化，并以方位角0°～30°范围内平均RCS作为标准，优选出直切翼尖的方案。为了进一步探究直切方案下直切位置对前向RCS的影响，本文设计了六个直切位置不同的直切翼尖方案，并将它们在0°迎角下的H-H极化与V-V极化特性进行了对比分析。结果表明，直切位置为参考线15%处的直切方案具有最优的前向RCS特性，且相比于原始翼尖，其H-H极化下前向RCS平均值降低了0.78 dBm2。

本文相关工作为翼尖电磁散射特性研究提供了一定的补充，作为将来的潜在方向，全频段飞翼无人机翼尖的多形设计分析和隐身约束下的翼尖自适应变形非常具有研究价值。