圆弧形截面的翼尖几何修形方法研究

金 鼎 / JIN Ding

(上海飞机设计研究院，上海 201210)

圆弧形截面的翼尖几何修形方法研究

金 鼎 / JIN Ding

(上海飞机设计研究院，上海 201210)

现代飞机外形设计越来越注重局部细节的精细化设计，翼尖局部修形便是其中一项重要的工作。针对翼尖截面形状，分析并总结出两种圆弧形截面的翼尖几何修形方法。

翼尖；修形；圆弧形截面

0 引言

现代飞机外形设计越来越注重局部细节的精细化设计，如翼梢小翼设计、翼根前后缘边条设计、整流鼓包流线型设计、局部扰流装置设计等。

翼尖修形也属于外形精细化设计的其中一项，区别于翼梢小翼设计，翼尖修形指的是对原始翼面末梢的平面形状或者垂直于弦向的截面形状进行局部优化[1]，如图1所示。本文主要对翼尖截面形状以及圆弧形截面修形方法进行讨论。

图1 翼尖平面形状和截面形状优化

1 翼尖修形截面分类

翼尖修形截面按截面形状可分为近矩形、近三角形、斜切形、圆弧或近圆弧形，如图2所示。

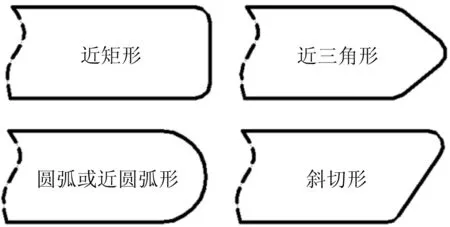
图2 翼梢修形截面形状分类

其中，近矩形截面翼尖修形仅仅对翼尖端肋的直角边进行了倒圆过渡处理；而近三角形截面翼尖修形是简单地对翼尖上下表面进行了切削，这样可以在一定程度上降低翼尖涡强度。以上两种截面的翼尖修形在早期的螺旋桨式飞机机翼上可以见到，采用这两种翼尖修形主要受当时加工工艺水平所限，随着制造水平的提升，现代飞机已很少采用。

斜切截面翼尖修形是将翼尖下表面进行切削，使翼尖局部形成上反，减小翼尖涡流强度，使之产生类似于翼梢小翼的作用。斜切截面翼尖又称霍纳翼尖，在目前的小型飞机上仍有较多的应用。

圆弧或近圆弧形翼尖截面是目前采用最为广泛的一种翼梢修形截面，机翼、翼梢小翼、水平尾翼、垂直尾翼、鸭翼、腹鳍等翼面类末梢均可以看到它的身影。其中，圆弧形截面翼尖沿垂直于翼尖弦线方向的截面处是由圆弧构成的，而近圆弧形截面翼尖沿垂直于翼尖弦线方向的截面则是二次曲线、三次曲线等非圆弧曲线构成。

相对于近圆弧形截面翼尖，圆弧截面翼尖各截面参数只需用一个半径值就可表达，因此在设计唯一性、制造及制造符合性检测便利性方面均有一定优势。虽然圆弧截面翼梢具备诸多优点，但是由于在几何成形时唯一的参数半径值也被翼型的当地截面厚度所限定，因此要真正实现圆弧形截面翼尖修形是比较困难的。

为实现圆弧形截面翼尖，下文将对几何修形方法进行深入探讨。

2 问题描述

假设已知一个翼曲面和翼梢端肋弦线，沿垂直于端肋弦线方向作任一截面，该截面与翼曲面相交产生三段截面线，如图3所示。

图3 翼尖圆弧截面

圆弧截面翼尖修形要达到的目的是使在翼尖处的截面线为圆弧形，且基于曲面光顺原则[2]，圆弧与修形前的三段截面线应尽量做到相切。

基于上述问题，本文分析并总结出两种圆弧形截面的翼尖几何修形方法，为了便于分析并使问题简化，下面在阐述过程中，仍取翼尖沿垂直于弦线方向的任意截面进行分析。同时，在翼尖修形时，一般是分别对翼曲面两侧分别修形，只要保证两侧修形曲面相切即可，因此翼尖修形进一步简化为单侧翼面上的修形问题。

3 半径扫掠法

某单侧翼曲面在翼尖处沿垂直于弦线方向的截面如图4所示，其中设线段AB为翼曲面弦平面的截面线，线段AC为翼尖端肋平面的截面线，线段CD为翼曲面的截面线。

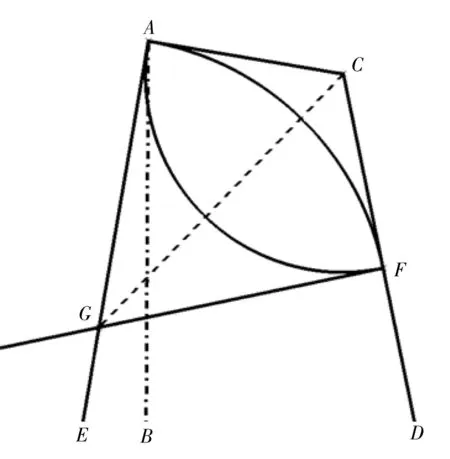
图4 半径扫掠法原理

参照图4，在该截面上作出与线段AC和线段CD同时相切的圆弧方法如下：

1)过A点作线段AC的垂线AE；

2)以点C为圆心，线段AC为半径作圆弧，圆弧与线段CD交点为点F；

3)作过点F并垂直于线段CD的直线，交线段AE于点G；

4)由全等三角形判断方法可知三角形ACG与三角形CGF为全等三角形，故AG与GF相等。则以点G为圆心，以线段GF为半径作圆弧，该圆弧必过点A，即点A和点F均为该圆弧的切点，由此可知该圆弧与线段AC和CD均相切。

上述过程分析了半径扫掠法在任一截面上的修形原理，具体到三维翼曲面，可以利用CATIA软件中扫掠模块，交替使用扫掠模块下的圆心半径扫掠功能和参考曲面扫掠功能，来实现圆弧截面翼尖修形。

基于半径扫掠法，在对某翼曲面进行翼尖修形的实际操作中，发现虽然修形后所得圆弧曲面与翼曲面可以做到完全相切，但同时圆弧曲面与端肋弦线有一定偏差，统计结果显示最大偏差值约为1.1mm，有80%的区域偏差小于0.5mm，如图5所示。

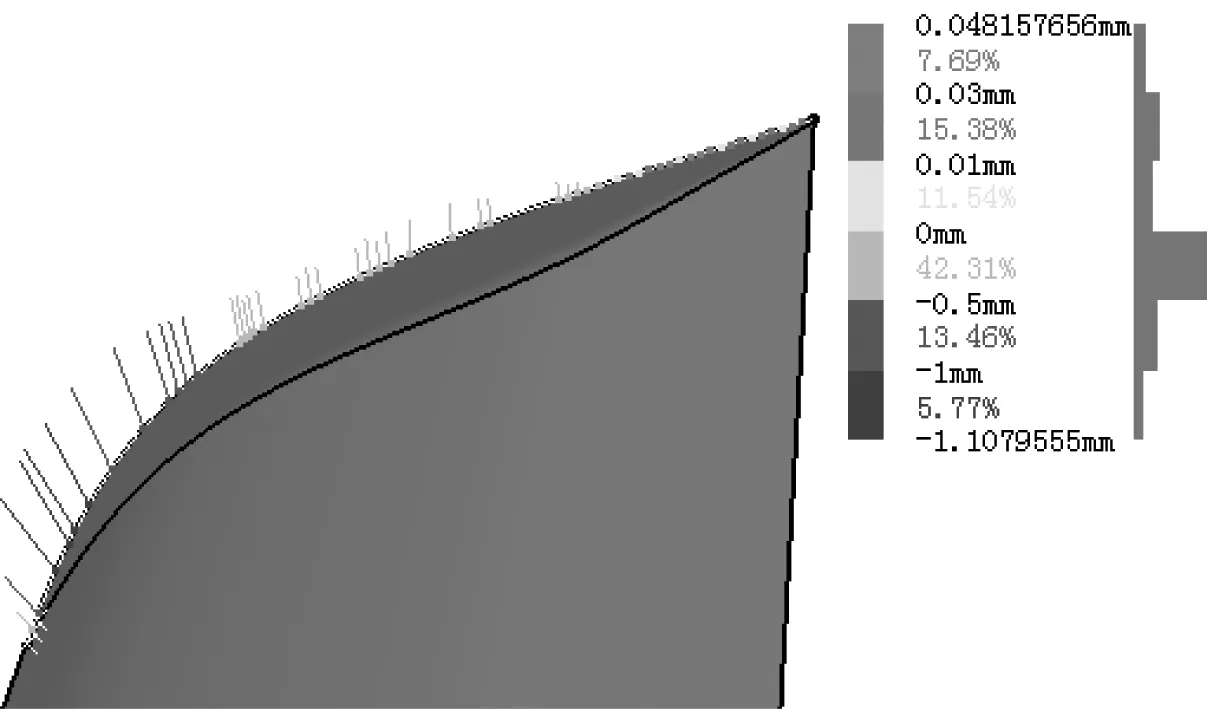
图5 偏差分析

分析问题原因，发现对于三维翼曲面，在翼尖处的任一截面与翼曲面的交线并非直线，即图4中CD为直线段的假设为理想状态，实际上CD为曲线，由此造成线段AG与线段GF不相等，修形后圆弧也就不通过点A。因此，对于不对称翼型翼曲面，两侧翼面分别修形后在端肋弦线处会产生间隙，故该方法仅适用于对称翼型翼曲面。

4 双切法

某单侧翼曲面在翼尖处沿垂直于弦线方向的截面如图6所示，其中设线段AB为翼曲面弦平面的截面线，线段AC为翼尖端肋平面的截面线，线段CD为翼曲面的截面线。

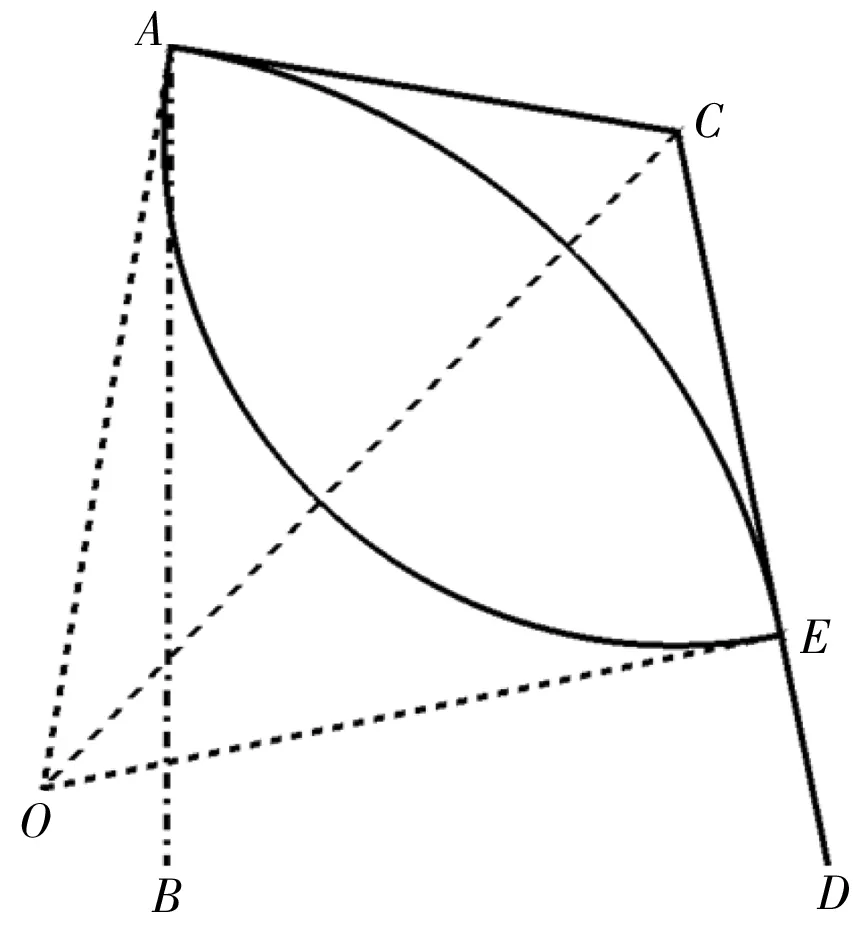
图6 双切法原理

参照图6，在该截面上作出与线段AC和线段CD同时相切的圆弧方法如下：

1)以点C为圆心，线段AC为半径作圆弧，圆弧与线段CD交点为点E；

2)过点A和点E，作一在点A处与线段AC相切的圆弧，圆弧圆心为O。因线段AC与线段CE相等，由由全等三角形判断方法可知三角形ACO与三角形CEO为全等三角形，故点E也为线段CD的切点，可知该圆弧与线段AC和CD均相切。

以上分析了双切法在任一截面上的修形原理，具体到三维翼曲面，可以利用CATIA软件中扫掠模块，使用扫掠模块下的圆心半径扫掠功能和双引导线相切面扫掠功能，来实现圆弧截面翼尖修形。

基于双切法法，在对某翼曲面进行翼尖修形的实际操作中，发现虽然修形后所得圆弧曲面可以和端肋弦线完全重合，但同时圆弧曲面与翼曲面的交线处并不完全相切，分析结果显示圆弧曲面与翼曲面连接处有约70%的区域切矢连续性偏差小于0.5°，如图7所示。

图7 连续性分析

分析问题原因，同样是由于翼尖处的任一截面与翼曲面的交线并非直线，即图6中假设的线段CD实际为曲线，故修形后圆弧与曲线CD在点E处不一定相切。针对这一问题，当切矢连续性偏差足够小时，工程应用中是可以忽略不计的，而对于切矢连续性偏差稍大的区域，可以进行局部二次光顺处理。事实上，翼尖修形曲面与翼曲面近似相切的情况，在不少机型上也均能见到。

5 应用实例

在某型号预研工作中，用到了本文所提到的两种圆弧形截面翼尖修形方法。

对于采用对称翼型的垂直尾翼，使用半径扫掠法，翼尖修形结果如图8所示。沿翼尖弦线均匀取截面线，可以看出翼尖截面处处为圆弧形，且修形面与主翼面切矢连续。

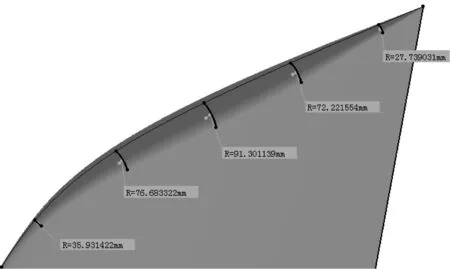
图8 半径扫掠法应用实例

对于采用非对称翼型的水平尾翼，使用双切法，翼尖修形结果如图9所示，可以看出修形后翼尖靠近前缘附近位置存在黑线，说明该处切矢不连续，其余位置均已做到切矢连续，且翼尖截面处为圆弧形。

图9 双切法应用实例

对于前缘附近切矢不连续曲面，对其局部裁切并做光顺修补处理，处理后的曲面已做的全部切矢连续，如图10所示。

图10 局部光顺处理

6 结论

本文对翼尖截面形状进行了研究，分析并总结出两种圆弧形截面的翼尖几何修形方法，并得出以下几点结论：

1)圆弧截面翼尖在设计唯一性、制造及制造符合性检测便利性方面均有一定优势；

2)半径扫掠法可以做到曲面完全切矢连续，但仅适用于对称翼型的翼曲面翼尖修形；

3)双切法适用于任何翼型的翼曲面翼尖修形，但翼尖修形曲面与翼曲面之间切矢连续性存在局部性偏差，工程应用时应考虑此偏差是否可忽略，否则需进行局部光顺处理；

4)为弥补半径扫掠法和双切法的不足，后续应进一步研究翼曲面的参数化表达，并通过软件二次开发来实现圆弧截面翼尖修形。

[1] 傅建明.低阻翼尖优化设计研究[J].民用飞机设计与究，1997，2.

[2] 程不时主编.飞机设计手册第5册：民用飞机总体设计[M].北京：航空工业出版社，2003.

Study of Shape Modification Methods for the Arc Profile Wing Tip

(Shanghai Aircraft Design and Research Institute, Shanghai 201210, China)

More and more attention is paid to the detail design of modern aircraft geometrical configuration. The local shape modification of the wing tip is one of the important aspect. Two methods of local shape modification for arc profile wing tip are summarized and analysed in this paper.

Wing Tip; Shape Modification; Arc Profile

10.19416/j.cnki.1674-9804.2016.04.013

V222

A