橡胶混凝土单轴压缩应力应变全曲线数学描述

胡仁桂

（江苏省建工建材质量检测中心有限公司，江苏 南京 210008）

0 引言

采用废旧橡胶颗粒制备橡胶混凝土能够有效减小废旧橡胶对环境的污染，同时能够充分利用橡胶韧性高和阻尼性能好等优点，为实际工程应用提供新的建筑材料[1-3]。文章探究了橡胶掺量对混凝土弹性模量和单轴抗压强度等力学性能的影响，并在此基础上建立了能够合理描述橡胶混凝土应力应变全曲线的统计损伤模型。通过模型计算结果与不同橡胶掺量条件下的橡胶混凝土单轴压缩试验结果进行对比，取得了良好的拟合效果，表明该模型能够用于描述橡胶混凝土的基本力学特性。

1 橡胶掺量对混凝土力学特性的影响

图1为不同橡胶掺量条件下橡胶混凝土的单轴压缩应力应变曲线实验结果。从图1可以看出，随着橡胶掺量的逐渐增大，试样的单轴压缩强度和切线模量均会逐渐减小，峰值强度对应的轴向应变则会逐渐增大，表明掺入橡胶颗粒能够显著提高混凝土的延性。

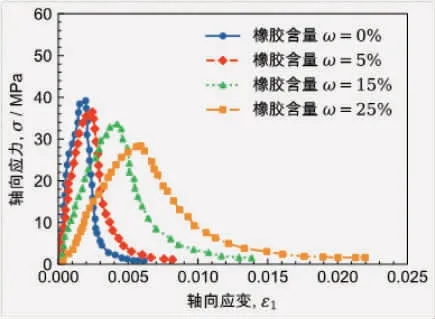
图1不同橡胶掺量混凝土的单轴压缩应力应变曲线

橡胶混凝土的弹性模量、峰值强度及其对应的轴向应变随橡胶掺量的变化规律如图2所示。从图2可以看出，弹性模量和峰值强度会橡胶掺量的增加而近似的呈线性减小趋势，而峰值强度对应的轴向应变则会逐渐增加。

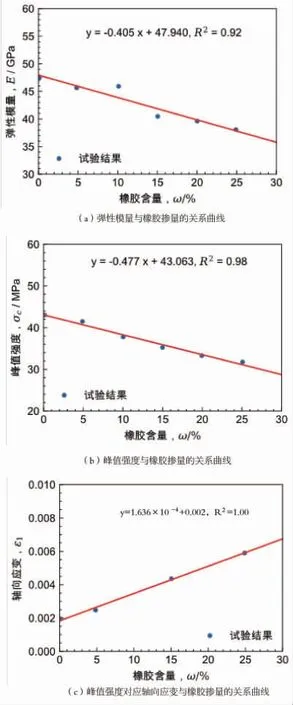
图2 橡胶混凝土的弹性模量、峰值强度及其对应的轴向应变随橡胶参量的变化规律

2 橡胶混凝土单轴压缩本构模型

2.1 统计损伤模型

在统计损伤力学中，通常定义已经破坏的微元数Nd与总的微元数N之间的比值为损伤因子D，如式（1）所示：

对于含N个微元的橡胶混凝土试样，在一定加载范围内发生破坏的微元数Nd，如式（2）所示：

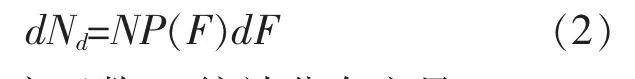
式中：P（F）概率密度函数，F统计分布变量。

假定微元破坏概率服从Weibull分布，并且是关于轴向应变ε1的函数，因此P（ε1）表示如式（3）所示：

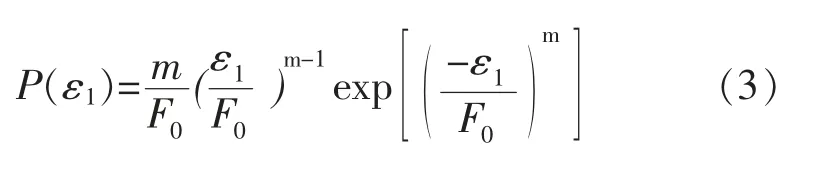
式中：m、F0-Weibull统计分布参数。

对式（2）进行积分并将其代入式（1）中，可以得到伤因子D关于轴向应变ε1的表达式如式（4）所示：

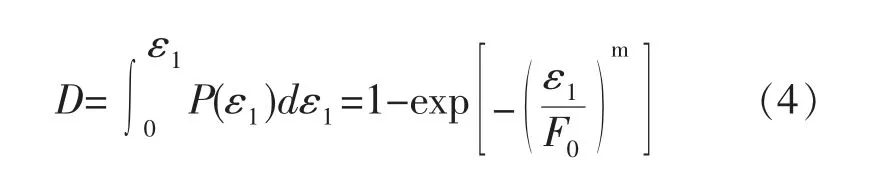
损伤因子D可以用于表征橡胶混凝土的损伤程度，当D=1时，根据Lemaitre应变等价性假定，橡胶混凝土内部将形成大量的空洞，并且完全丧失承载力。

根据Lemaitre应变等价性假设，在外部荷载作用下可以认为橡胶混凝土由损伤和未损伤两部分材料组成，并且损伤部分材料不具有任何承载能力。在此基础上，可以将橡胶混凝土的动态损伤模型如式（5）所示：

式中：E-橡胶混凝土的弹性模量；σ1-轴向应力。

材料参数m和F0可以根据橡胶混凝土的弹性模量E、峰值强度σpeak及其对应的轴向应变εpeak计算得到，如式（6）、（7）所示：

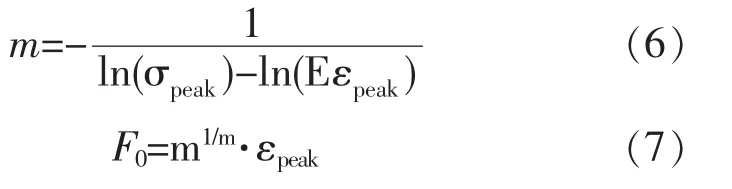
2.2 模型验证

为了验证上述橡胶混凝土的统计损伤模型的适用性，采用该模型对前文中给出的橡胶混凝土单轴压缩试验结果进行计算，材料参数如表1所示。

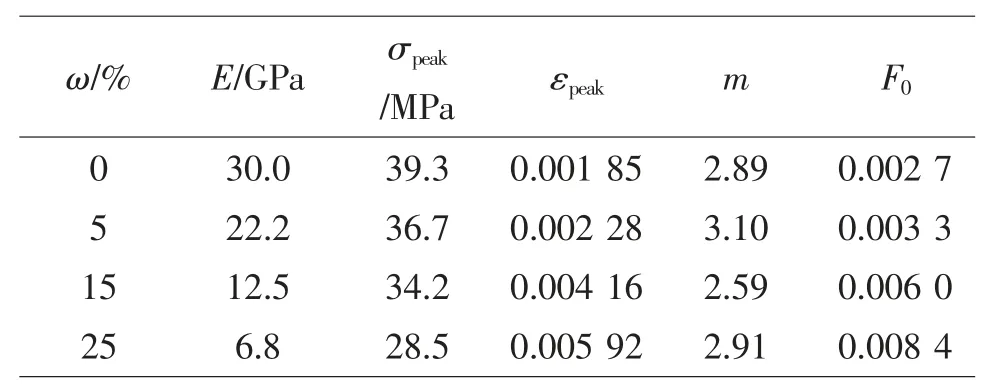
表1 橡胶混凝土统计损伤模型材料参数

不同橡胶掺量对应的橡胶混凝土的单轴压缩应力应变全曲线实验结果和模型计算结果如图3所示，两者十分接近，由此可以看出该模型能够合理地描述橡胶掺量对混凝土基本力学特性的影响。但是，模型计算得到的橡胶混凝土峰后应力应变曲线与实验结果之间存在一定的偏差，有必要对模型做进一步的修正。

图3不同橡胶掺量条件下混凝土的单轴压缩应力应变曲线实验结果和模型计算结果对比

模型计算结果同时表明，增大橡胶掺量会导致橡胶混凝土的峰值强度和切线模量明显减小，而试样的延性则会显著增加。不同橡胶掺量条件下试样的损伤因子D随轴向应变ε1的变化规律如图4所示。由图4可以看出，随着橡胶掺量增大，试样的损伤速率会逐渐减小，因此在外部荷载作用下试样更容易发生延性破坏。

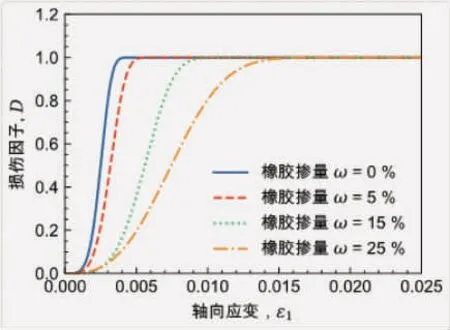
图4不同橡胶掺量条件下混凝土的单轴压缩试验损伤因子随轴向应变变化规律

3 结论

（1）橡胶混凝土的强度会随着橡胶掺量的增加而逐渐减小，但由于橡胶颗粒具有较好的阻尼性能，试样的峰值强度所对应的轴向应变会与橡胶掺量之间满足线性增长规律，此时试样更容易发生延性破坏。

（2）该模型具有形式简单且物理意义明确等优点，通过将模型计算结果与橡胶混凝土的单轴压缩试验结果进行对比，取得了良好的拟合效果，表明该模型能够合理的描述橡胶掺量对于混凝土基本力学行为的影响。

（3）模型计算得到的橡胶混凝土的峰后应力应变曲线与实验结果之间存在一定差异，在后续研究中需对其做进一步修正以改善模型的计算效果。