基于九轴惯性传感器的人体关节活动度测量方法研究

高 照，祝小波，寇晓洁

（陕西福音假肢有限责任公司，西安710016）

0 引言

现代医学康复领域通过让被测者做特定动作来测量其关节活动度，分析测量的结果后得出康复结论[1]。传统关节活动度测量方法为采用尺规法测量[2-3]，这种方法需固定关节另一端在已知角度且只能静态地测量关节的一维活动度；李文浩等[4]利用人体标记点配合摄像头测量被测者的关节活动度，该方法可实时测量关节活动度，但标记点若被阻挡会影响输出结果；使用惯性传感器测量人体关节活动度是一种无需依赖摄像头数量和环境光照的方法，赵晓皓等[5]提出了使用2 个六轴传感器分别在关节两端进行测量的方案，但2 个传感器需人为校准偏航角在同一坐标系内后方可进行测量，操作较为烦琐，除此之外，多个电路在分布式场景下同时测量还需要实现同步技术[6]。

鉴于此，本文采用九轴惯性传感器搭配无线处理器采集肢体的角速度、加速度、磁力原始数据，然后对这些数据进行校准，接着带入到Madgwick 算法求出在世界坐标系下的四元数，通过四元数计算出无需人为校准偏航角的欧拉角。最后通过将电路布置在关节两端的肢体上，求2 个电路输出的欧拉角差值得到该关节的活动度，与只测量关节一端肢体活动度的方法相比，本文方法不仅省去固定关节一端在已知角度的环节，而且能够减少因关节固定端肢体运动而造成的误差。

1 角度计算算法

常用的角度计算算法有以下3 种：（1）对角速度积分可求得响应较快的全姿态角度值，但该结果无法计算初始姿态角度并且受自身噪声累积影响会导致测量角度漂移；（2）对加速度计的三轴数据进行反三角函数计算可求得俯仰角和横滚角，但是其结果有滞后性且无法计算偏航角；（3）对磁力计的三轴数据进行反三角函数计算，可求得稳定的全姿态角度值，但是其结果也存在滞后性。为了结合这三者的优势，本文选择Madgwick 互补算法[7]进行姿态解算，并在姿态解算前选取均值滤波算法、几何校准算法[8-9]分别对角速度计、加速度计和磁力计进行校准。

1.1 Madgwick 算法

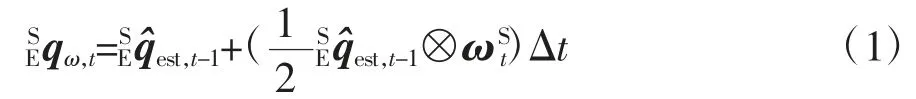
式中，Δt 为角速度计采样间隔。

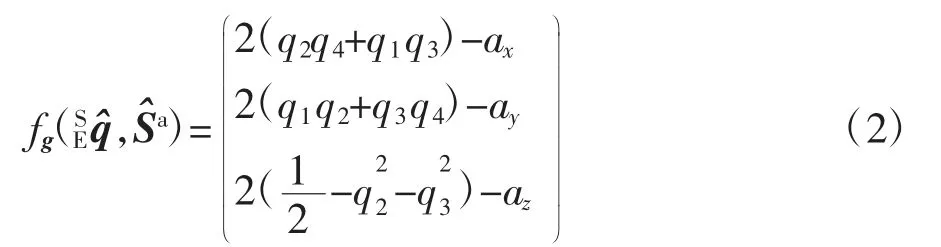
地磁场具有水平方向和垂直方向的分量，因此磁力计的向量式为=[0，mx，my，mz]，其中mx、my、mz分别是物体三轴磁力归一化后的值。记地磁向量为b^E=[0，bx，0，bz]，其中bx和bz分别为地磁场水平和垂直方向的分量，其目标函数可用公式（3）表示：

然而加速度计虽然可以快速计算出横滚角和俯仰角，但无法求出偏航角；磁力计虽然可以求出全姿态的欧拉角，但其响应速度远小于加速度计。因此需要将加速度计和磁力计的姿态进行融合，得到目标函数公式（4）。对公式（4）进行梯度下降可得公式（5），从而得到公式（4）中的最优解。 在公式（5）中μt为步长，梯度可通过求解目标函数的雅可比式得到，如公式（6）～（9）所示。

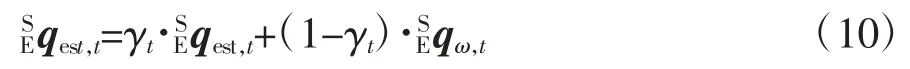
式中，γt为加权系数。

然而，若直接使用未校准的九轴惯性传感器数据进行姿态解算，其结果和真实姿态之间将存在很大偏差，因此在姿态解算前须对九轴惯性传感器进行校准。

1.2 角速度计校准

校准角速度计的目的是避免由于角速度计误差在长时间积分后导致姿态漂移，角速度计误差来源于传感器零偏、温度漂移。校准角速度计的数学模型为

式中，gyroraw为原始角速度数据；gyrooffset为偏移值。当角速度计静止的时候，原始数据减去偏移值应为零，因此可以通过将传感器静止放置一段时间后求得角速度计各轴的平均值来作为偏移值，参考设定的放置时间是60 s，则偏移值计算公式为

式中，gyrosum为60 s 内该轴角速度的数据和；samplesum为60 s 内该轴角速度的采样数量。

1.3 加速度计校准

在加速度计生产过程中，加速度计易产生零偏和敏感轴不正交，这会使得加速度计线性度漂移，影响俯仰角和横滚角的准确性。加速度计校准模型[10]如下：

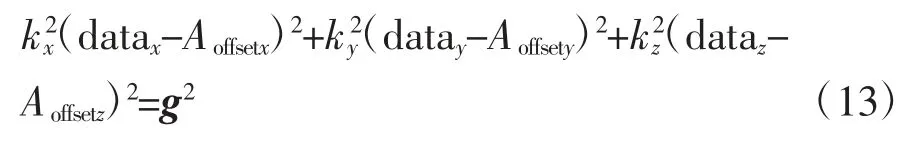
式中，ki为标度因子；Aoffsetx、Aoffsety、Aoffsetz分别为加速度计x、y、z 轴的加速度零偏；datai为归一化的三轴加速度计值（i∈{x，y，z}）。因为datai和g 是已知的，可知求出ki和Aoffseti需要采集6 个不同的姿态。本文选用的加速度计几何校准法流程图如图1 所示。具体流程如下：

图1 加速度计校准流程图

（1）摆放加速度计，在6 个姿态采集数据。6 个参考姿态分别与加速度计三轴正反方向重力轴方向一致。

（2）计算零偏。在计算零偏时需与第一步同步进行，在摆放加速度计姿态过程中对数据进行如下处理：

式中，M 为采集次数；Arawxi、Arawyi、Arawzi分别为加速度计三轴原始数据。使用高斯消元法[11]求解（XTX）β=XTY 中的加速度零偏矩阵β 后，记即加速度计x 轴、y 轴、z 轴的零偏Aoffsetx、Aoffsety、Aoffsetz。

（3）提取敏感姿态数据。加速度计三轴中某一轴加速度绝对值越大，则重力轴和该轴夹角越小。记绝对值最大的轴为敏感轴，为了保证计算标度因子准确性，需要求敏感轴与重力轴夹角在一定范围内，可设置剔除夹角阈值为10°，在采集加速度过程中，加速度计的轴向和重力方向夹角若大于10°，则剔除该部分数据。

（4）求解标度因子。使用加速度原始值减去第二步求得的零偏后，将公式（13）变换后可得到在不同位置提取的敏感轴原始均值减去零偏后的差值矩阵：

公式（16）中各项计算公式如公式（17）～（19）所示：

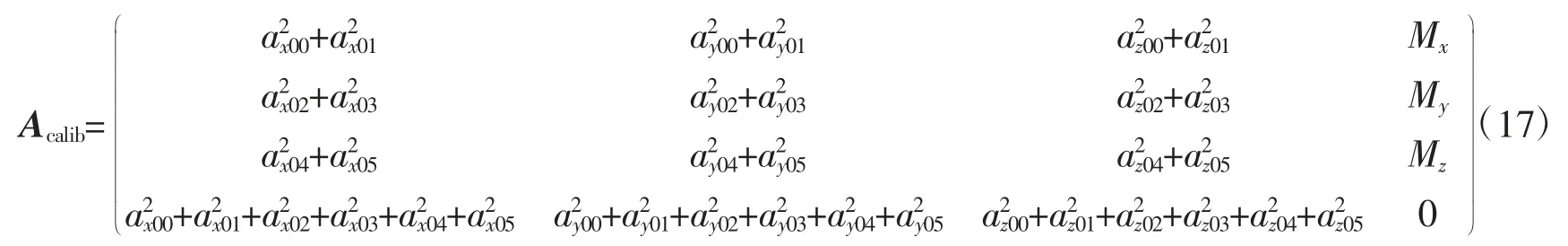
在矩阵Acalib中，aαβ、aαγ、aαδ（α∈{x，y，z}，β∈{00，01}，γ∈{02，03}，δ∈{04，05}）表示在不同位置提取敏感姿态数据后敏感轴原始值减去零偏后的均值；KS矩阵为标度因子矩阵；Mx、My、Mz为加速度计重力原始值的2 倍，MS为加速度计重力原始值的6 倍。求解线性方程公式（16）易得KS，最后对KS各元素开根可求得x、y、z 三轴的标度因子。

（5）将上述求得的零偏Aoffsetx、Aoffsety、Aoffsetz和标度因子kx、ky、kz带入到公式（20）中，即可校准加速度计。

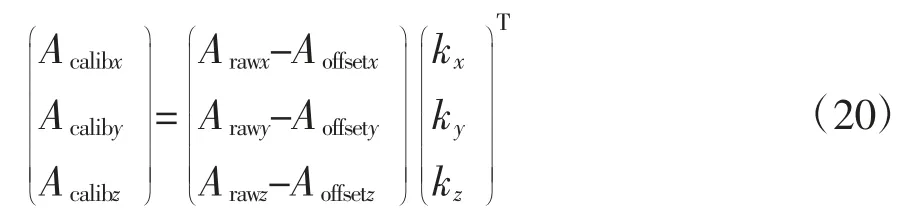
1.4 磁力计校准

因为每一个电路会受到不同软磁场和硬磁场干扰，这会导致偏航角数值不一致，所以磁力计校准的目的是将多个关节活动度测量电路的偏航角统一在世界坐标系内。本文基于几何校准法[8-9]列出磁力计零偏线性方程，使用高斯消元[11]求解磁力计零偏线性方程。校准过程中需将磁力计在空间中绕中心点自由旋转，磁力计的数据会组成一个球面[9]，经校准后该球面的球心坐标将处于（0，0，0）。以下是数据处理方法：

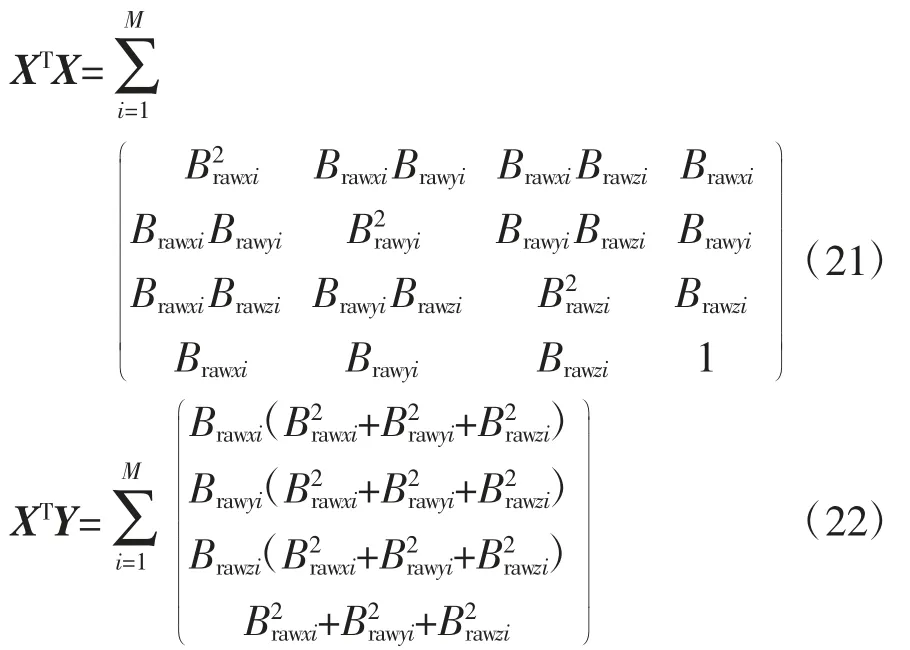
式中，Brawxi、Brawyi、Brawzi分别为磁力计三轴原始数据。求解（XTX）β=XTY 中的β 后，记即磁力计x、y、z 轴的零偏Boffsetx、Boffsety、Boffsetz，最后将磁力计各轴原始值和零偏作差即完成校准。

2 关节活动度测量电路设计

关节活动度测量电路由无线处理器、九轴惯性传感器、同步电路、电源管理模块和唤醒关机电路组成，如图2 所示。

图2 关节活动度测量电路框图

图3 为无线处理器电路原理图。其中无线处理器为ESP32-WROOM-32D 模组，该模组不仅支持蓝牙4.2，而且支持Wi-Fi 通信，还具有集成电路总线（inter-integrated circuit，I2C）、串行外设接口（serial peripheral interface，SPI）、通用输入输出（general purpose input output，GPIO）接口和通用异步收发器（universal asynchronous receiver/transmitter，UART）、模拟数字转换器（analog-to-digital converter，ADC）等[12]。图3 中C8 和C9 为电源滤波电容；IO34 为GPIO 输入模式，用于判断电路是否在充电；IO35 为ADC 模式，用于判断电池电量；IO13 为GPIO 中断输入模式，用于判断是否读取九轴惯性传感器的更新数据；IO18和IO19 为I2C 模式，用于与九轴惯性传感器通信；IO16为GPIO 中断输入模式，用于判断是否进行同步；IO4为GPIO 输入模式，用于判断是否开关机。

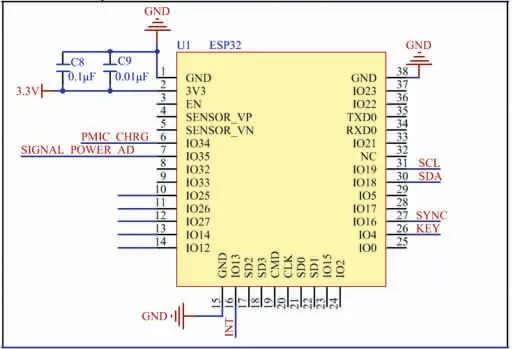
图3 无线处理器电路原理图

图4 为九轴惯性传感器电路原理图。传感器型号为MPU9250，该传感器集成角速度计、加速度计和磁力计，通信方式为I2C 和SPI，MPU9250 可以通过I2C配置为更新数据后INT 引脚输出脉冲信号[13]的模式。

图4 九轴惯性传感器电路原理图

图5 为同步电路原理图。其中R3 为充电保险电阻，其功能为过流保护；P1 是一种USB 插座，该插座的引脚4 与引脚5 不连接，其功能是将外部信号的地和关节活动度测量电路的地连接，还将P1 的引脚4 连接到无线处理器的IO4 引脚，由于外部电路已经和关节活动度电路共地，因此IO4 可以接收外部电信号。多个测量电路可用同步装置[14]同时输入一个电平信号，无线处理器可被触发GPIO 中断，其在中断服务中可清零内部时间戳，若计算机此时开始接收数据包，并且由于网络拥挤导致数据包接收顺序错误，可根据数据包上带有的时间戳重新对数据排序就能解决多个设备协作冲突的问题。其中数据包格式包含帧头、数据包长度、设备编号、数据值和时间戳。

图5 同步电路原理图

电源管理模块由电源管理芯片电路和稳压电路组成，其电路原理图如图6、7所示。电源管理芯片型号为LTC4067EDE，其中引脚4、5和P1 的VCC_IN 连接，当充电器件P1 的引脚1 有5 V 电源接入时，LTC4067EDE 的引脚10 可给外接电池充电，同时使得其引脚2 变为低电平通知无线处理器此时为充电状态。R7、R8 和R10 组成的分压电路对锂电池电压进行分压，锂电池分压后的低压节点SIGNAL_POWER_AD 和无线处理器主引脚IO35相连，无线处理器使用模数转换功能可实现电池电量的采集。稳压芯片型号为TPS73133，其中引脚1以及引脚3 与电源管理芯片电路的VOUT 连接，分别用于给TPS73133 输入电能和使能芯片；磁珠L1和电容C3 组成滤波电路，使TPS73133 引脚5 输出的电源纹波降低。

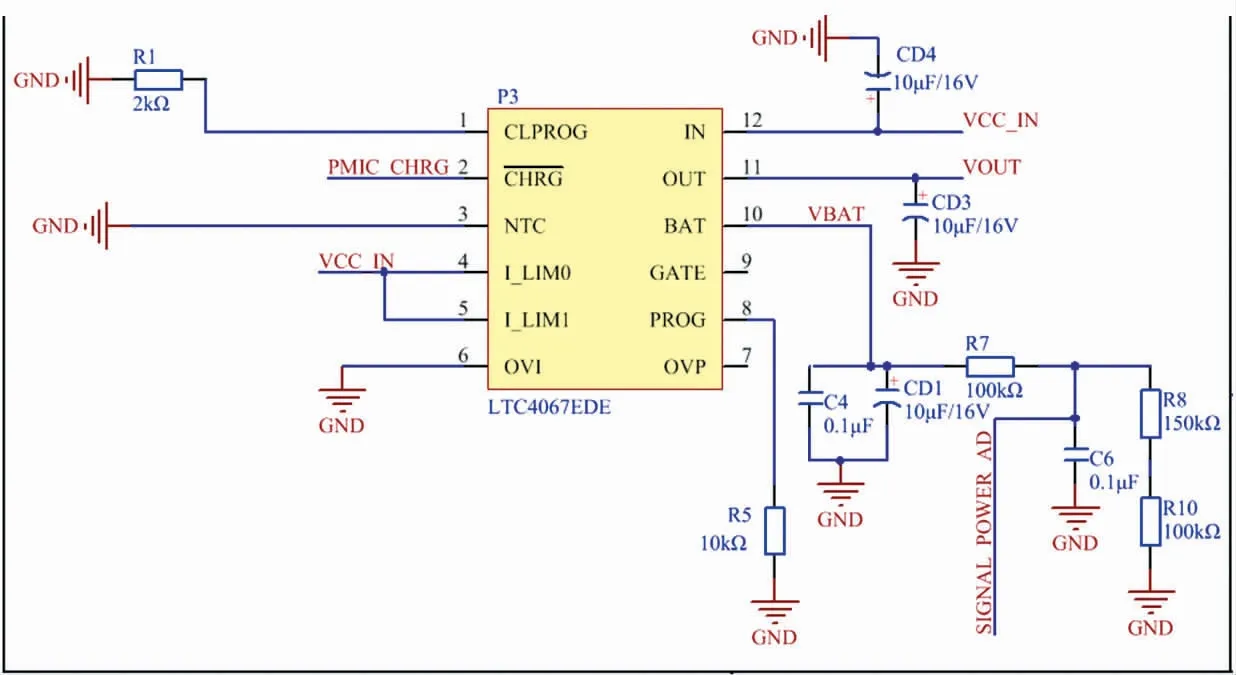
图6 电源管理芯片电路原理图

如图8 所示，唤醒关机电路包含上拉电阻R17、微动按键P15 和滤波电容C17，当微动按键按下后KEY 节点为低电平，无线处理器根据KEY 节点电平状态与持续时长实现唤醒与关机功能。

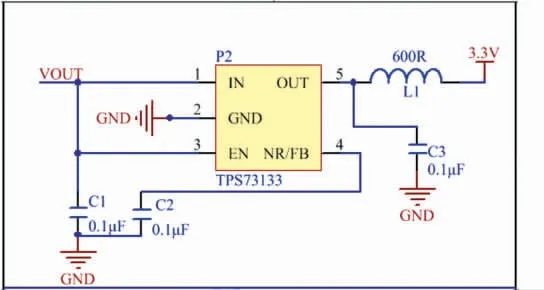
图7 稳压电路原理图

图8 唤醒关机电路原理图

整个电路可通过Wi-Fi 或蓝牙和计算机进行交互，计算机需配备无线路由器或蓝牙适配器。图9 为关节活动度测量电路电路板实物图，电路板的尺寸为30 mm×35 mm（长×宽）。

图9 关节活动度测量电路电路板实物图

3 校准结果和同步功能测试结果

3.1 角速度计校准结果

图10、11 为角速度计校准前后自身的噪声变化对欧拉角的影响。由图10 可看出，校准前角速度计的噪声长时间积分导致欧拉角漂移。由图11 可看出，校准后角速度计噪声降低，从而减少了欧拉角的漂移误差。

图11 校准后的角速度和欧拉角波形

3.2 加速度计校准结果

图12（a）、（b）为加速度计校准前的原始值，轴向绝对值近似8 000，图12（c）、（d）为加速度计经过校准后的原始值，轴向绝对值近似5 000，乘以最小有效位（1/4 096）g（g 为重力加速度）进行校准后，加速度计真实值更接近1g。对比表1 和表2 中6 个姿态下的俯仰角、横滚角及三轴加速度值，可知校准前后加速度计所测得的角度与关节量角器的测量结果相比，误差明显减少，分别为±2°～±7°与±1°。因此加速度计的校准提高了欧拉角精度。

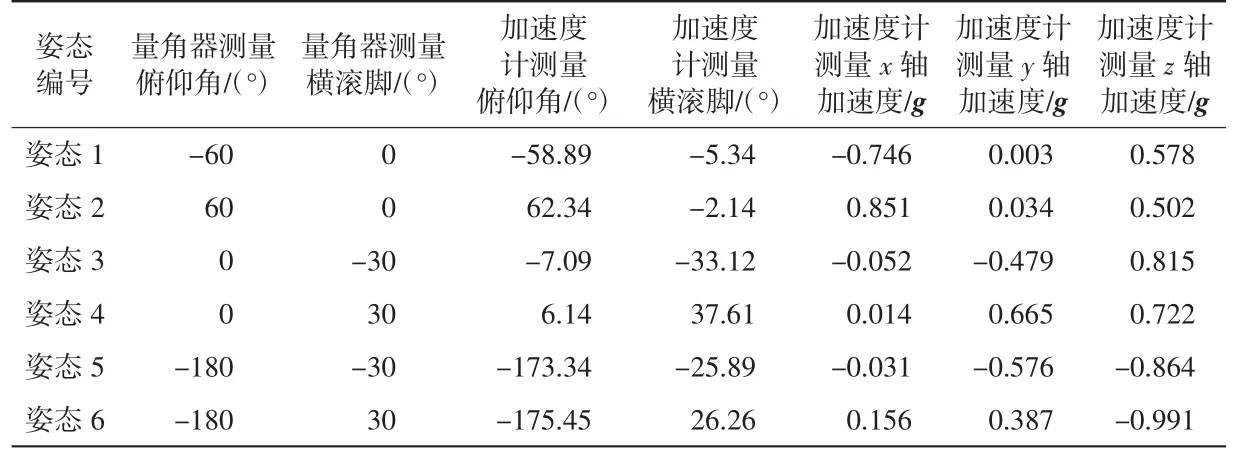
表1 校准前的加速度、欧拉角测量结果

表2 校准后的加速度、欧拉角测量结果

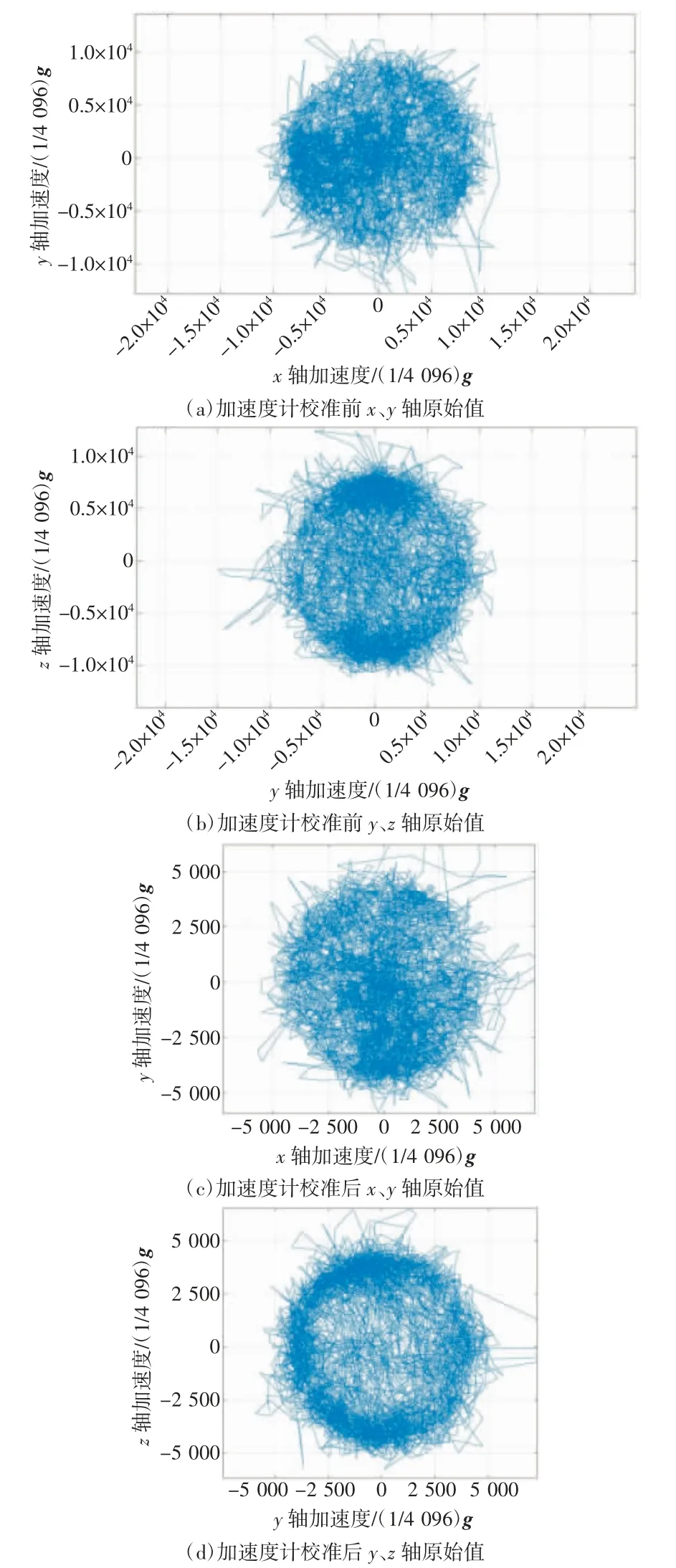
图12 加速度计校准前后原始值

3.3 磁力计校准结果

由图13 可以看出，磁力计校准前磁力球面圆心坐标为（-0.1，-0.2，0），进行校准后磁力球面的球心回到（0，0，0），这意味着几何校准算法消除了软硬磁场的干扰。

在校准了磁力计后，开始验证引入磁力计是否会使得偏航角一致。在验证过程中需保证2 个关节活动度测量电路的姿态一致，再通过这2 个电路输出的角度数据判断误差，其一致性测试结果见表3。由表3 可知在4 个姿态下2 个电路的俯仰角和横滚角误差为±1°，偏航角误差能达到±1°，说明引入了磁力计使得偏航角得到了统一，而且没有降低俯仰角和横滚角精度。

表3 一致性测试结果 单位：（°）

3.4 同步功能测试

开启2 个关节活动度测量电路向计算机发送数据，未同步的数据包接收示意图如图14（a）所示，可以看出同一时间点下，2个电路的数据由于内部时间戳（TS）不一致，上位机无法辨识在现实环境中2 个数据是否为同时测量的，因此无法进行数据分析。从图14（b）同步后的数据包接收示意图可以看出，内部时间戳一致时可以对数据进行协同分析。另外图14（b）中还模拟了一种由于数据堵塞导致电路2 没有及时处理t2时间段的数据包的场景，但由于时间戳（TS）是统一的，因此在t3时刻接收来自t2的数据包后，仍可通过计算机将2 个电路的数据按时间戳重新排列求差，进而获取关节活动度。

图14 数据包接收示意图

4 颈椎活动度测量实验

为了使测量结果不失一般性，使用关节活动度测量电路测量一名志愿者的颈椎活动度。将测量电路分别佩戴在志愿者额头及胸部中央，开始测量前对2 个电路进行同步操作，然后引导志愿者头部左右侧屈、前后屈伸、左右旋转，测量电路通过Wi-Fi 将头部、胸骨体欧拉角发送到计算机，使用MATLAB 将头部欧拉角减去胸骨体欧拉角获得颈椎关节活动度。实验结果表明颈椎活动度符合人体特征。

4.1 颈椎前后屈伸活动度

颈椎前后屈伸活动度波形如图15 所示。其中图15（a）中俯仰角为兴趣角度，-77.33°、-156.20°分别表示头部前屈、后仰角度。从图15（b）中可知，颈椎前后屈伸过程中身体无法保持完全静止，会随着颈部活动向同侧倾斜，产生误差，对应的角度为-113.70°和-116.00°。当用头部欧拉角减去胸骨体欧拉角后，其余2 个角度基线降低至0°，俯仰角分别为36.37°和-40.20°，而颈椎前后屈伸范围[15]是35°～45°，因此该结果符合人体关节活动度特征。

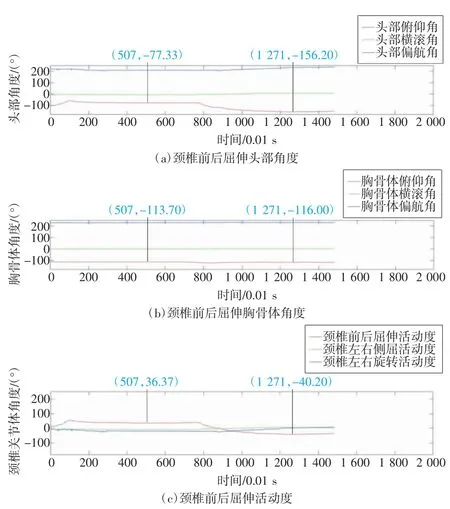
图15 颈椎前后屈伸活动度波形

4.2 颈椎左右侧屈活动度

颈椎左右侧屈活动度波形如图16 所示。由于测量方式和4.1 章节类似，只是兴趣角度改为横滚角，因此使用相同的处理方法，用头部横滚角减去胸骨体横滚角，最终得到颈椎左右侧屈活动度分别为30.37°和-30.04°，该结果也符合颈椎左右侧屈特征（0°～45°）[15]。

图16 颈椎左右侧屈活动度波形

4.3 颈椎左右旋转活动度

在测量颈椎左右旋转活动度过程中，为了规避万向节死锁问题，需改变电路摆放方向，所以图17 中头部和胸骨体的初始俯仰角和横滚角为0°。最终，颈椎左右旋转活动度剔除误差后的结果分别为62.60°和-60.14°，该结果同样符合颈椎左右旋转活动度特征（60°～80°）[14]。

图17 颈部左右旋转活动度波形

5 结语

本文提出了一种基于九轴惯性传感器的人体关节活动度的测量方法，并针对该测量方法提出了相应的角度计算算法和电路设计方案。其中角度计算算法使用均值滤波算法和几何校准算法对传感器进行校准，然后再使用Madgwick 算法计算姿态角度，保证输出的欧拉角在同一坐标系内且精度为±1°。提出的电路测量方案具备无线传输功能和硬件同步功能，使电路可布置在关节两端协同测量。另外，在颈椎活动度测量实验中利用关节两端肢体角度差值来反映关节活动状况，可降低因关节另一端运动引起的误差，验证了测量方法的准确性和有效性。

但本研究也存在一些不足之处：（1）在测量过程中由于欧拉角存在万向节死锁的问题，要根据测量情况调整电路摆放位置，后续研究可以寻求新的角度计算方法。（2）应用实验只使用2 个采集电路测量了颈椎活动度，后续研究可以利用更多传感器同时采集多个肢体活动度并加入神经网络算法、支持向量机等算法来得到辅助性的诊断意见。