基于IGA-SVR随机Hough变换的预制构件螺栓孔节点定位

段中兴，郭沛菁

(1.西安建筑科技大学 信息与控制工程学院，西安 710055；2.西部绿色建筑国家重点实验室，西安 710055)

0 引言

预制混凝土构件是装配式建筑的基本元素，构件干式连接技术是指在连接时不浇筑混凝土的情况下，直接将预制构件焊接或使用螺栓连接，在螺栓连接装配过程中，构件边缘预留螺栓孔，将螺杆穿束进入相邻构件的螺栓孔中完成安装[1]。传统的装配过程主要由建筑机械设备将预制构件运送至指定地点，在人工搬扶的配合下完成安装。这样的过程效率低下且安全保障困难。在如今工业生产现场大量使用机器人的环境下，可将自动装配机器人与机械设备结合进行安装工作。因此预制构件节点定位是自动装配机器人待解决的关键问题。

螺栓孔是一种圆形结构，对于圆形检测技术，Paul Hough提出了霍夫变换，将二维平面空间的边缘点映射到参数空间，用大多数曲线边沿点所满足的特定参数模型去描述图像中的边界曲线，但传统的霍夫变换需要累加统计峰值，计算复杂且鲁棒性较弱。蔡佳等[2]针对霍夫变换类圆检测方法所需参数较多的问题，提出一种基于梯度的局部增长和距离矩形统计图的快速圆检测方法。根据梯度模量值和方向的局部增长得到圆弧线段求解圆心。该方法对不同尺寸的圆有良好检测效果，但对于尺寸较小的圆检测精度欠佳。王宪等[3]提出一种应用区域估计的方法检测有背景干扰下的多个圆，根据霍夫变换前2帧图像初始化Sage-Husa滤波器，对有效区域进行估计结合图像增强方法实现多圆精确定位，测试精度显著提高。彭永志等[4]提出了一种基于DBSCAN随机圆检测算法，通过DBSCAN聚类算法分割感兴趣的圆形特征，根据最小二乘法和径向扫描得到圆形外边缘点，利用重复圆检测得到圆心。但算法中参数需通过实验估计，因此结果具有不确定性。Scitovski等[5]提出了一种利用改进k-mens算法的圆形定位方法，利用Hausdorff距离区分各圆。Jiang[6]提出了一种使用概率密度和改进兴趣点的随机霍夫变换，通过改进样本特征点并寻找候选圆来提升随机霍夫变换的检测效率，但对于图像存在噪声较大的情况还需进一步改进。

以上研究通过不同方法对Hough变换算法进行改进均取得良好效果。但近年来利用人工智能算法结合Hough变换的研究较少。本文针对预制构件螺栓孔节点在定位时现场环境复杂，图像采集角度多变以及螺栓孔存在凸起凹陷并非规则平滑圆形导致定位精度及定位效率低下的问题。对遗传算法(GA，genetic algorithm)引入收缩包围与螺旋更新机制改进算法局部搜索能力，并对交叉变异算子引入收敛因子提高后期搜索效率，优化支持向量回归(SVR，support vector regression)参数，训练逼近螺栓孔圆形的超平面方程，对该模型运用随机Hough变换确定螺栓孔圆心坐标，通过视差计算螺栓孔三维坐标，实现对预制构件螺栓孔节点的定位。

1 相关原理介绍

1.1 随机Hough变换算法

Hough变换通过大多数边缘点都满足的特定参数表达式去描述图像中的曲线，将二维直角坐标系下图像中的直线或曲线转换至参数空间中的一点，通过不断累积形成峰值，使复杂的图像问题转换为局部极大值检测问题，是圆形检测的有效方法[7-11]。对于普通二维坐标系下的一个圆，其半径为定值，而圆周上边缘点组成的点集映射到参数空间中为一系列以各边缘点为圆心，半径相等的圆锥。三维参数空间的圆两两相交，随着映射点的增加，三维圆锥面会有一个共同的交点，此点即为所求图像圆心。其基本思想是证据累积，在进行圆形检测时将普通坐标系中圆上的点转换到参数空间，实际应用中，圆形边缘的每一点都需要参与计算，三维空间下证据累积所消耗的时间与存储空间较大，不仅加大系统存储，还降低了运行效率。因此，研究者们在Hough变换基础上提出随机Hough变换。通过随机选取圆周上3个不共线的点计算参数定位圆。

直角坐标系中圆一般方程为:(x-a)2+(y-b)2=r2，参数空间下的方程为：(a-x)2+(b-y)2=r2。二维空间中圆心(a，b)对应参数空间中(a，b，r)。如图1所示，对于二维坐标系下圆A边缘上一点(x1，y1)，转换到参数空间中对应着一个以(x1，y1)为圆心，r为半径的竖直三维圆锥。(x1，y1)约束了通过该点一簇圆的参数。对于圆周上其它两点(x2，y2)、(x3，y3)同理可得相应圆锥面，由图1可知，以r为半径的3个圆交点即为所求圆圆心。

图1 随机Hough圆检测原理图

1.2 支持向量回归分析

支持向量回归是一种基于统计理论的机器学习方法，通过样本训练找到一回归平面，使得集合中所有数据到该平面距离最短[12-14]。对于给定训练集，SVR线性回归模型为：

S={(x1,y1),…,(xn,yn)},xn∈R,yn∈Rf(x)=

ω·x+b

(1)

其中：ω为超平面法向量，b为常数。在SVR解决非线性问题时通过引入核函数Φ(x)将输入数据映射到高维空间，在高维空间中进行线性求解从而解决原空间的非线性问题，具有处理大规模数据集的能力，如图2所示，ε为容忍误差，是实际值y与f(x)之间的最大允许误差值，当y落入f(x)±ε内时，都被认为分类正确。尽可能使得f(x)与实际值y无限接近，当f(x)与y差值大于ε才计算损失。

图2 非线性SVR原理示意图

针对本文螺栓孔为圆形图案，样本均为非线性数据集，回归模型为：

f(x)=ω·Φ(x)+b

(2)

为包容回归平面部分异常数据点，引入松弛变量ζi、ζi*后SVR的目标函数可表示为：

(3)

且满足：

(4)

其中：C为惩罚参数，表示系统模型对误差的容忍程度。n为训练样本个数。引入拉格朗日乘子αi，αi*，最初的回归模型可表示为：

(5)

式中，K(xi,yi)为核函数，核函数的选择是影响SVR算法处理性能的关键之一，本文核函数选择高斯径向基核函数(RBF)，该核函数目前应用广泛、预测精度相对较高且函数插值能力较强。其数学表达式如下：

(6)

σ为核函数参数，表示高斯径向基核的核宽度。

1.3 遗传算法

遗传算法是基于达尔文生物进化论思想，模仿自然界生物进化机制的一种启发式优化算法[15-16]。该算法通过适应性函数来衡量每个解决方案的优劣，通过模拟自然界的物竞天择法则和遗传物质的交叉互换和突变现象不断更新和优化种群，保持适应度高的基因遗传到下一代，适应度低的基因被淘汰，直至搜索到种群最优值。主要通过选择、交叉、变异3个步骤寻找目标最优解。选择操作通过对种群适应度评估选择适应度高的个体到新种群中，交叉操作是指将种群中染色体交叉从而形成新的优秀个体，变异操作指在染色体的一点进行突变产生新个体。

正是由于选择、交叉、变异等步骤，使得遗传算法具有全局搜索能力且自适应性强。但这样的过程容易导致算法易“早熟”，局部搜索能力欠佳且后期收敛速度慢。

2 基于改进遗传算法的IGA-SVR随机Hough变换定位圆算法

2.1 基于动态收敛因子的交叉变异算子

对于遗传算法后期收敛速度慢、搜索效率低的问题，对自适应交叉变异算子引入收敛因子λ，可根据迭代次数快速调整当前交叉变异概率。收敛因子公式如下：

(7)

其中：t为当前迭代次数，tmax为种群最大迭代次数，参数λ反映了当前系统迭代情况。改进后交叉变异算子公式如下：

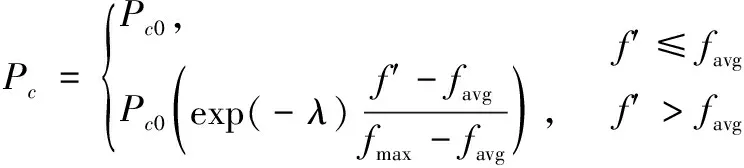
(8)

(9)

其中：Pc0为初始交叉概率，f’为交叉个体中较大的适应度值，Pm0为初始变异概率，f为变异个体当前适应度值，fmax为种群最大适应度值，favg为种群平均适应度值。

进化初期，种群间个体差异较大，适应度较低，此时交叉变异概率保持初始状态有利于丰富种群多样性，随着系统迭代次数增加，在迭代后期种群适应度逐渐趋于稳定且满足算法要求时，为不破坏种群中优质个体同时不影响算法的收敛速度，引入收敛因子，λ逐渐减小，搜索空间相应缩小，因此改进后的算法能够有效提高后期收敛效率以及搜索速度。

2.2 引入收缩包围与螺旋更新机制

在遗传算法进行变异操作时，对于种群内优质个体应采用较低变异概率与变异方式，对于劣质个体应采用较高变异概率与变异方式。同时，为了提高算法局部搜索能力，引入收缩包围与螺旋更新的局部寻优机制。根据参数A对种群局部搜索或全局搜索方式进行调节。

A=2ar1-a

(10)

(11)

其中：r1为[0,1]内的随机数，t为当前迭代次数，tmax为最大迭代次数。参数A随a的变化而变化，在种群迭代初期，a值较大，参数A较大，此时算法全局搜索能力较强；而在迭代后期随着不断更新优化，此时种群平均适应度较高，a值较小，参数A相应较小，当|A|<1时，种群通过收缩包围或螺旋更新方式进行局部寻优。两种局部搜索方式概率相同，均为0.5，当概率小于等于0.5则采用收缩包围方式进行寻优，当概率大于0.5时采用螺旋更新方式进行寻优，通过[0,1]范围内产生随机数p确定搜索方式。该机制公式如下：

(12)

其中：X*(t)为当前最优解位置向量，X(t)为当前解位置向量，b为常数参数，l为[0,1]内的随机数，D为种群最优个体与当前个体的距离，即：

D=|CX*(t)-X(t)|

(13)

C=2r2

(14)

式中，r2为[0,1]内随机数。

3 基于IGA-SVR的随机Hough变换预制构件螺栓孔节点定位流程

为使SVR训练出更准确的超平面方程，使用改进的遗传算法建立IGA-SVR模型，对SVR进行参数寻优，并结合随机Hough变换定位圆。算法流程如图3所示，具体步骤如下：

1)初始化算法各参数。设置初始迭代次数T=0，随机产生遗传算法的初始种群，对SVR参数进行编码，每个染色体表示为：{Xi:Ci，σi，εi}。

2)适应度评价。适应度是衡量种群及个体优劣的标准，下式为适应度评价函数。

(15)

其中：N为评估样本数目，为第i个输入的真实值，SVRi(xi)为支持向量回归对第i个输入的模型预测值。计算种群适应度并记录最优个体。

3)选择操作。采用轮盘赌法筛选出合适的个体作为下一代亲本。

4)根据参数A进行全局或局部寻优。若|A|<1，种群通过收缩包围或螺旋更新机制进行局部寻优，否则根据改进的交叉变异算子进行更新。

5)判断是否满足终止条件。比较当前个体与历史最优个体适应度，选择最优值作为本次迭代最优个体。当达到最大迭代次数或满足适应度要求停止循环，否则跳转至步骤2)。

6)SVR分析。将IGA得到的参数带入SVR模型并根据圆形训练集求得逼近螺栓孔圆形的超平面方程f(x)。

7)随机Hough变换定位圆。将螺栓孔测试集带入f(x)，判断是否属于圆形边缘点，任取圆周上非共线的三点进行随机Hough变换定位圆。

图3 改进算法流程图

4 实验及结果分析

为验证IGA算法有效性，实验分为两部分。第一部分选用4个标准测试函数验证IGA算法相较于GA算法的优化性能；第二部分将IGA算法应用于SVR参数寻优结合随机Hough变换对螺栓孔进行检测定位，并与仅使用随机Hough变换、基于GA-SVR的随机Hough变换检测结果对比，证明了IGA-SVR随机Hough变换算法的定位精度更高。计算机为Windows10 64 bit操作系统，2 G独立显卡，软件部分由Matlab R2019a完成。

4.1 测试函数实验分析

4个常用标准测试函数如表1所示，其中函数f1～f3为单峰值，f4为多峰值，全局最优值均为0。分别使用IGA算法与GA算法进行寻优，独立运行30次记录结果。种群初始规模设为50，迭代次数设为200，交叉概率初始为0.8，变异概率初始为0.1。

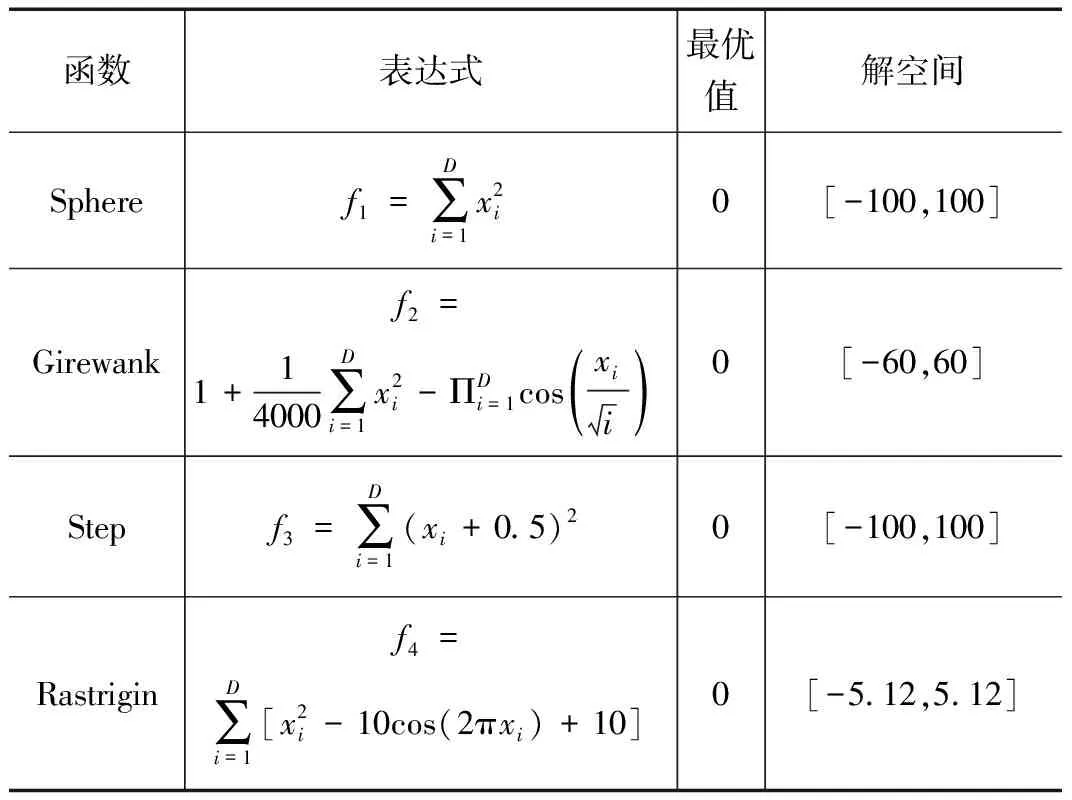
表1 标准测试函数

IGA算法与GA算法对各测试函数运行30次后结果如由图4与表2所示。由实验结果可知，4种测试函数在IGA算法与GA算法优化下均可收敛并得到函数最优值。如图4(b)、(c)所示，对于函数f2和f4，IGA算法可快速收敛到目标最优值，收敛速度快且有效避免了局部极值。图4(a)、(d)中，函数f1和f3都呈快速下降趋势，寻优精度分别达10-3、10-5，最终也能够找到最优解0。其中，Rastrigin函数收敛精度最高，寻优能力最强。

图4 4种测试函数迭代曲线

表2 4种标准测试函数实验结果

综上所述，对于选取的4个测试函数，改进后算法的最小值、平均值以及标准差均小于GA算法。可以看出该算法能够快速搜索到全局最优解，搜索精度高，最大收敛能力以及收敛速度更强且稳定性较好，是一种快速稳定的全局优化算法。

4.2 螺栓孔三维坐标定位实验

4.2.1 双目视觉相机标定

双目视觉是依据人体视觉系统的一种三维距离测量方法，通过设置两台摄像机仿照人眼，对同一目标点进行拍摄，根据视差获取目标位置[17-18]。平行双目视觉系统成像原理如图5所示。

图5 平行双目视觉系统原理图

Pw为定位目标点，Ocl、Ocr为双目相机的光心，两光心之间的距离为基线b，成像平面到摄像机光轴的距离为焦距f。根据相似三角形原理可得目标点深度信息，即：

(16)

因此为获取相机参数，本次标定实验采用张正友相机标定法[19-20]，利用Matlab完成摄像机标定。标定板为5×7棋盘格，单元格边长27 mm，在ZED相机视野范围内，通过不断改变棋盘格位姿，采集19组标定板照片。标定后，左右相机内参矩阵如下：

相机外参数旋转矩阵与平移矩阵分别为：

4.2.2 三维坐标定位实验

在使用本文所提算法进行螺栓孔节点定位时，遗传算法初始种群数M=50，最大迭代次数T=100。交叉概率初始为0.8，变异概率初始为0.1。当优化参数满足适应度要求或达到最大迭代次数终止程序并将参数带入SVR模型。经多次迭代，适应度曲线如图6所示，种群最优适应度达83.146%，此时，SVR惩罚参数C=153.294 3,σ=0.027 1,ε=0.460 3。

图6 改进遗传算法适应度曲线

针对预制构件中螺栓孔的检测，分别使用传统随机Hough变换、基于GA-SVR的随机Hough变换与本文所提的IGA-SVR随机Hough变换进行检测。双目相机获取图像后，对预制构件连接节点图像进行预处理，包括图像灰度化、提取螺栓孔边缘信息等步骤。之后进行圆形检测与定位，如图7所示。对比分析可以看出，对于圆形螺栓孔边缘不规则且噪点较多的情况，随机Hough变换检测结果偏差较大，IGA-SVR随机Hough变换检测到的圆较GA-SVR算法更加贴近螺栓孔实际位置。检测后的左右图像根据双目视差计算三维坐标，以左相机光心为原点，得到结果如表3所示。

表3 检测圆心三维坐标

图7 3种算法检测结果

4.2.3 实验结果分析

被测预制构件模型尺寸为50 mm×50 mm×100 mm，与双目摄像机距离155 mm，相邻螺栓孔圆心距为30 mm。双目视觉定位系统选取左相机为基准相机，世界坐标系原点为左相机的光心。表4为双目视觉检测圆心Z方向上测量坐标与理论距离的误差结果。最低误差为1.112%，最高误差为3.14%，平均相对误差为2.09%，绝对误差保持在3.25 mm，均在误差允许范围内。而A、C两点相对误差较大，这与构件模型纹理较弱，检测出的特征点与实际特征点还存在一定偏差有关，需进一步提升测量精度。

表4 Z方向定位精度

表5、表6、表7分别为传统随机Hough变换算法、GA-SVR随机Hough变换与IGA-SVR随机Hough变换定位误差结果。通过测量螺栓孔圆心坐标，将测量圆心距与实际圆心距进行对比，用以评价在X、Y轴的定位精度。传统随机Hough变换最大测量误差达7.860%，平均相对误差5.190%，误差较大，基于GA-SVR的随机Hough变换误差次之，本文提出的IGA-SVR随机Hough变换定位误差均小于以上两种算法，最大绝对误差为1.414 mm，平均相对误差为2.022%，有效提高了圆心测量精度。综上所述，基于IGA-SVR的随机Hough变换算法在定位螺栓孔圆心时满足精度要求并且能有效减小定位误差。

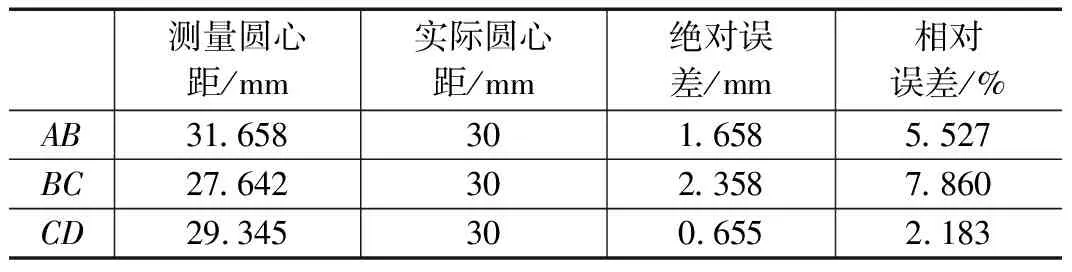
表5 随机Hough变换算法误差

表6 GA-SVR随机Hough变换算法误差

表7 IGA-SVR随机Hough变换算法误差

最后，分别统计3种算法实验耗时平均值，结果如表8所示。总体上传统的随机Hough变换算法检测时间最短，基于GA-SVR的随机Hough变换算法与本文所提IGA-SVR的随机Hough变换算法耗时相对稍长。这是由于随机Hough变换算法仅取圆上的三点坐标进行定位，数据量极少，但也导致了定位不精确的问题。联合算法运行时需通过遗传算法进行多次迭代选择最优SVR模型参数，SVR模型中核函数将低维数据映射到高维空间，在高维空间中构造训练数据的最优分类超平面，提高精度的同时增加了时间的开销。在后两种联合算法用时相近的情况下，改进后的算法定位精度以及稳定性更佳。

表8 各算法所需时间

5 结束语

本文提出了一种基于改进遗传算法优化SVR参数的随机Hough变换算法，并应用于检测预制构件螺栓孔节点三维坐标。通过对遗传算法引入收敛因子及收缩包围与螺旋更新机制，改进算法收敛速度慢的问题，同时提高局部搜索能力。通过实验分析，结果表明，基于IGA-SVR的随机Hough变换算法相较于传统随机Hough变换在定位误差中得到有效减小，螺栓孔平均定位误差由5.19%减至2.02%，最大绝对误差不超过1.5 mm，Z方向平均相对误差为2.09%，均满足工程定位精度需求，具有良好的定位效果。但在算法运行时间方面仍可进一步研究，尽量降低时间成本。