基于阵列式磁传感器的电力设备接地网定位方法研究

辛明勇，徐长宝，田 兵，刘 仲，刘子轩，3，鲁彩江，3

（1.贵州电网有限责任公司电力科学研究院，贵州贵阳 550002；2.南方电网数字电网研究院有限公司，广东广州 510000；3.西南交通大学机械工程学院，四川成都 610031）

0 引言

接地网的导体大多使用铜、镀锌钢或覆铜钢等材料，根据国内外相关研究可知，在腐蚀性强的土壤中接地网导体腐蚀速率可达3.4 mm/a，严重时可达8 mm/a。由于接地网一般敷设在地下0.3～1 m 深处，因此不能直观的判定其位置及腐蚀状况。传统的探测方法有整体开挖法、选点开挖检查法、摇表测量接地电阻法。传统探测方法的缺点在于盲目性大，在消耗大量人力、物力、财力的同时阻滞电力系统的正常工作[1-4]。

对接地网腐蚀状态进行探测前，首先要对接地网方位及深度进行探测。目前存在的接地网定位及腐蚀程度探测方法主要有电化学法、电网络法、多信息融合法以及电磁法等[5-8]。电化学法通过测量金属与土壤间腐蚀体系的电化学特性（包括击穿电位、腐蚀电流等）来确定接地导体的腐蚀情况，但是该方法无法判断出接地网的断点情况[9-11]。电网络法是指将接地网等效为纯电阻网络模型，通过测量接地引下线节点间的电气特性值而建立接地网诊断方程，求解并分析对应的电气特性（通常为电阻、电压）变化规律，但是当接地体存在局部侵蚀时，其电阻及电压变化值很难获取[12-17]。多信息融合法即结合多种方法对接地网状态进行探测，能够同时探测腐蚀程度和腐蚀速率等指标，提高接地网探测的可靠性和实用性[18-23]。电磁法是基于电磁感应原理的探测方法，通过测量接地网导体产生的磁场来判断接地网导体的方位、深度信息以及腐蚀程度[24-31]。

与电化学法、电网络法、多信息融合法相比，电磁法可准确判断出接地网的断点情况，且原理简单、应用方便。因此，本文基于电磁法的电磁感应原理，采用交流电激励测量法对电力设备接地网进行研究与探测，旨在解决测量装置移动不便以及难以精确探测接地导体方位及深度的问题，实验表明采用电磁法可为电力设备状态检测提供准确的数据依据。

1 传感器阵列结构设计与距离分析

1.1 传感器阵列结构设计

通过接地引下线施加异频正弦交流电时，接地网在其正上方地表处激发的磁感应强度主要取决于激励电流的大小、接地体埋设深度等因素。根据接地网磁感应强度探测范围及分辨率的需要，在工程实践中常用磁通门传感器以及各向异性磁阻（Anisotropic Magneto Resistance，AMR）传感器来采集磁感应强度。磁通门传感器的优点在于鲁棒性好，但其价格昂贵、体积大、频率响应较低、现场功耗较大。AMR 传感器的优点在于成本低、尺寸小、分辨率高、温度稳定性好、抗干扰能力强、现场功耗低等。在实际测量过程中为了尽量排除外部干扰，对频率响应有着较高的要求，同时考虑到现场功耗以及便携性，本文选用AMR 传感器来采集磁感应强度。

本文设计的接地网定位及腐蚀程度探测探头的传感器布局示意图如图1 所示。图1 中，x，y，z为三维空间坐标轴，1-5 号传感器在同一水平面上，Δh为5 号和6 号传感器之间的垂直距离，Δl为1 号与3 号传感器之间的水平距离。

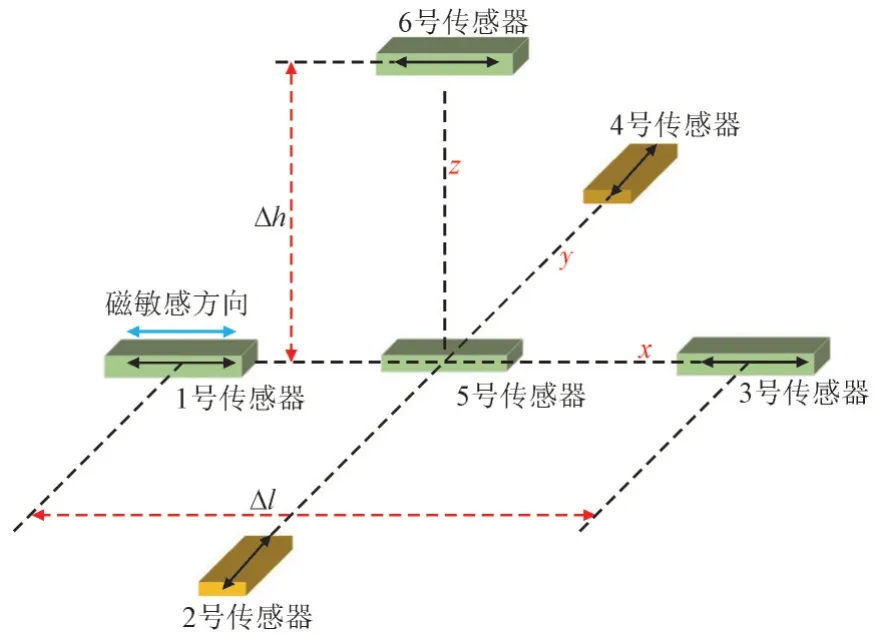
图1 接地网定位及腐蚀程度探测探头的传感器布局示意图Fig.1 Grounding grid positioning and corrosion degree detection probe sensor layout

由图1 可知，采用1-4 号传感器所测磁场数据可确定接地导体的方位，采用5 号和6 号传感器所测磁场数据可计算接地导体的深度，采用5 号传感器所得磁场数据可判断接地导体的腐蚀状态。

由于传感器的设置位置直接影响到探测深度的准确性，所以计算确定1 号与3 号、2 号与4 号、5号与6 号传感器之间的距离就显得十分重要。已知空间内某一点的磁感应强度与该点的三维空间坐标有直接关系，而探测接地网深埋时不仅与三维空间的坐标有关，更与5 号和6 号传感器之间的高度差值Δh有关。因此必须先确定传感器之间的距离，再通过控制变量法将后续测定接地网深度时的变量进行缩减，以保证计算结果的有效性和准确性。本文在对接地网定位及腐蚀程度探测探头传感器距离进行理论分析时，设定矩形接地装置边框值为16 m，接地网深度范围为0.3～2 m，探测探头距地面高度为0.1 m，将接地网深度和探测探头距地面高度相加得到探头探测深度为0.4～2.1 m。

1.2 传感器阵列距离分析

1.2.1 水平距离分析

图1 中，探测探头水平面上布置的1-4 号传感器主要进行接地导体的方位判断。由于4 个传感器距离探测探头中心的距离均相等，所以本文以1号传感器为例计算其到探测探头中心的最优水平距离为0.5Δl。本文选用的单轴线性磁阻传感器型号为HMC1001，其在水平面上测量磁场时与接地导体垂直方向测得的磁场值最大。由于接地网模型具有对称性，因此产生的磁感应强度也具有对称性。以第一卦限为例，对卦限内的磁感应强度（矢量）Bx分布进行理论分析与计算，即可计算出最优水平距离Δl。

传感器距离分析模型如图2 所示。

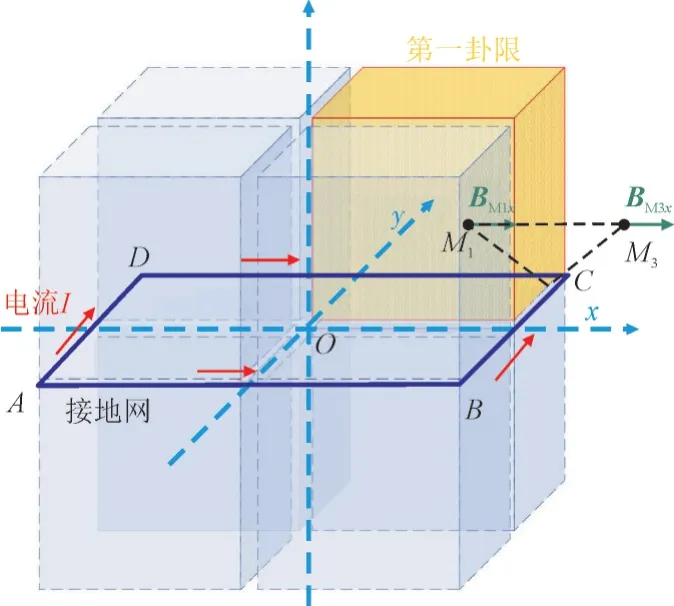
图2 传感器距离分析模型Fig.2 Sensor distance analysis model

图2 中，O为空间坐标系原点，A，B，C，D分别为接地网的4 个顶点，BM1x和BM3x（图2 中深绿色箭头表示其方向）分别为M1和M32 个点的磁感应强度。

本文利用CDEGS 仿真软件进行分析，由于阵列式传感器的体积不宜过大，因此传感器间水平距离的极限设置为0.4 m。本文选用接地导体材料为镀锌扁钢，每根接地导体长为16 m，横截面积为40 mm×4 mm，接地导体电阻率为1.78×10-7Ω·m，相对磁导率为200，激励电流的强度和频率分别为3 A和500 Hz，正极接点A 和负极接电C 的土壤电阻率均为300 Ω·m。

传感器间水平距离Δl值仿真验证结果如图3所示。图3（b）中，横坐标轴为图3（a）中观测线段L1L2上观测点在x轴上的坐标距原点O的距离。

图3 传感器间水平距离Δl值仿真验证结果Fig.3 Simulation results of horizontal distance Δl between sensors

由图3 可知，当1 号和3 号传感器之间距离Δl分别为0.10 m，0.15 m，0.20 m，0.25 m，0.30 m，0.35 m，0.40 m 时，测量并计算在观测线段L1L2上的1 号与3 号传感器的磁感应强度差值ΔB13的变化情况。观测线段起止点L1和L2的x，y，z轴坐标分别为L1（7.5，0，0.5）m，L2（8.5，0，0.5）m。无论Δl取何值，观测点位置越靠近接地导体，沿x轴方向上所测得的|ΔB13|值越小。在0.1～0.4 m 范围内，随着水平距离Δl的增大，ΔB13变化逐渐明显，最大值约为0.23 μT。探测探头传感器间水平距离Δl越大，磁感应强度差值ΔB13越大，越便于接地导体方位的判定。据此判断，探测探头结构尺寸不宜过大，本文选取Δl为0.4 m。

1.2.2 垂直距离分析

探测探头中5 号传感器位于探测探头的中心，6 号传感器位于5 号传感器正上方距离中心位置Δh处，通过联合计算5 号与6 号传感器测量磁场值可得到此时被测接地导体的深度信息。5 号传感器探测的沿x方向的磁感应强度为关于x，y，z的三元函数；6 号传感器探测的沿x方向磁感应强度为关于x，y，z，Δh的四元函数。

Δh为0.2 m 时，观测线段H1H2上计算深度与实际测量深度如图4 所示。观测线起止点H1和H2的x，y，z轴坐标分别为H1（8，0，0.4）m 和H2（8，0，2.1）m。

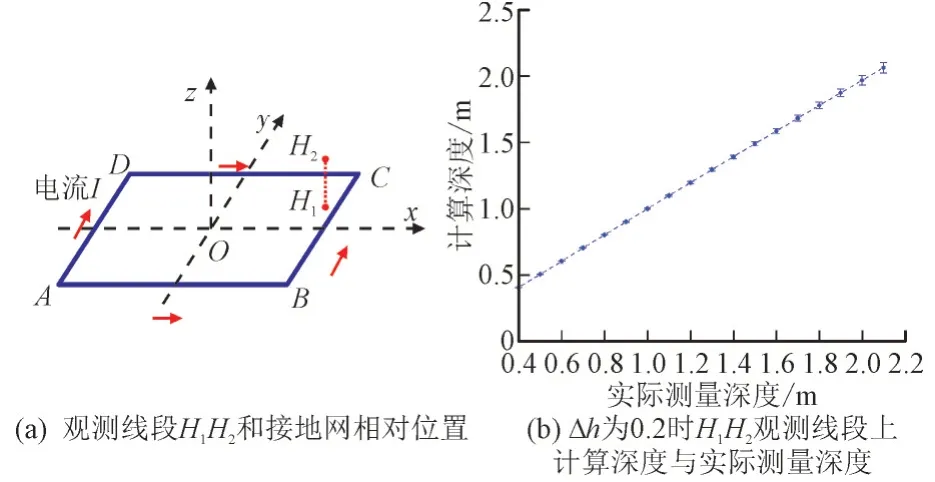
图4 观测线段H1H2上计算深度与实际测量深度Fig.4 Calculated depth and measured depth on observation line H1 H2

由图4 可知，当5 号和6 号传感器之间距离Δh为0.2 m 时，测量在观测线段H1H2上的5 号与6 号传感器的磁感应强度值，可计算出BC段接地导体的深度信息。随着实际深度的变化，计算深度值基本与实际深度一致，最大相对误差为1.86%。据此判断，在允许误差2%以内，本文选取Δh为0.2 m。

2 接地网定位方法

2.1 接地导体方位探测方法

对接地网进行定位首先要确定其埋设方向，方向指示方法如表1 所示。表1 中，B1，B2，B3，B4，B6分别为1，2，3，4，6 号传感器沿x轴方向上磁感应强度，表1 中方向参照图1，其中1，3 号传感器位置分别为正左和正右，2，4 号传感器位置分别为正前和正后，5 号传感器位置为居中。地下接地导体的埋设方位主要根据1，2，3，4，6 号传感器信号强弱进行判断，当B1，B2，B3，B4，B6满足表1 中的条件时可确定接地导体的埋设方位。

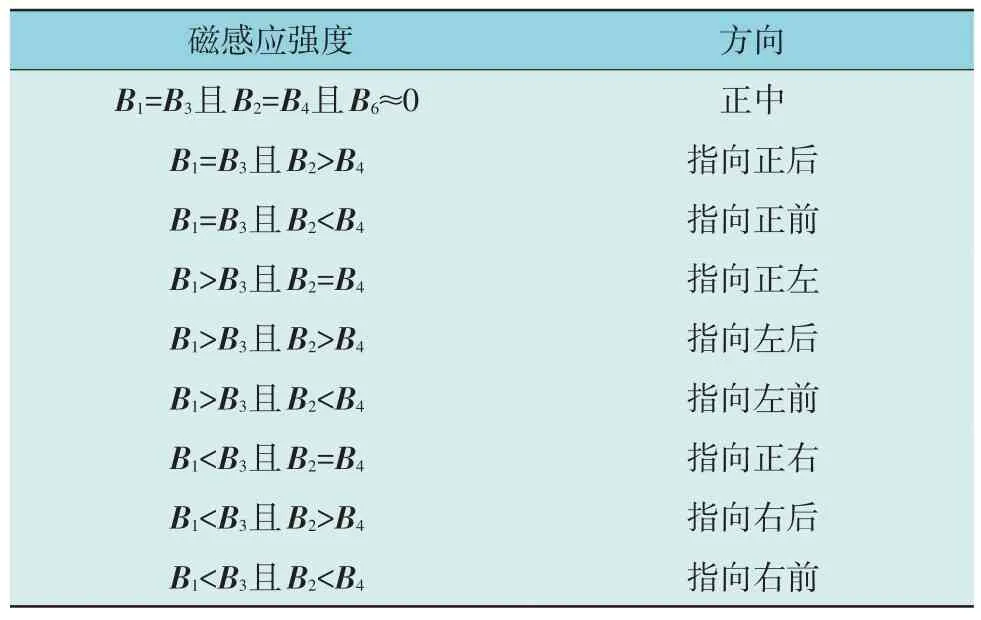
表1 方向指示方法Table 1 Orientation detection method

2.2 接地导体深度计算方法

在探测到接地导体的方位信息后，将探测探头置于被测接地导体中点的正上方（即ΔB13为0）。此时被测接地导体产生的磁感应强度远大于相邻接地导体在此处的磁感应强度，因此可只考虑被测接地导体产生的磁感应强度。利用5 号与6 号传感器的方位坐标联合计算5 号和6 号传感器测量值，得到被测接地导体的深度值。5 号与6 号传感器沿x方向的磁感应强度B5，B6分别为：

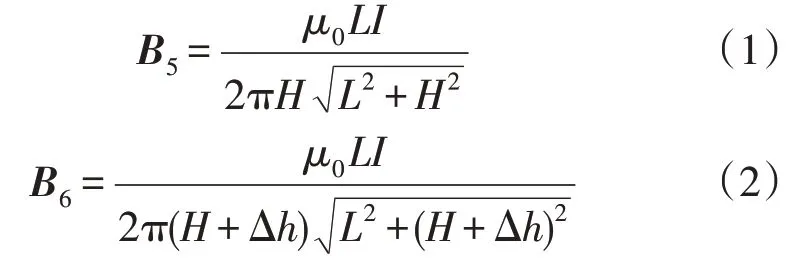
式中：μ0为真空磁导率；L为当前被测接地导体的长度；I为激励电流；H为探测探头距接地导体的垂直距离。

忽略外加激励电流不稳定的缺点以及泄漏电流对深度计算的影响，得到B5和B6的比值为：

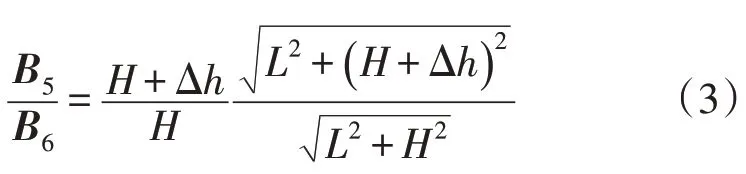
采用数值逼近的方法列方程求解H值为：

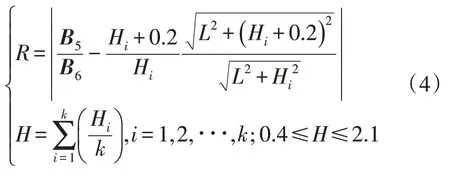
式中：R为深度计算精确值；Hi为第i次探测探头距接地导体的垂直距离；k为测量总次数。

为获得较为精确的深度计算值，R应尽可能小，本文取R≤10-6，即认为此时计算得到的H值符合探测要求。

3 接地网定位探测实验

3.1 接地导体方位探测实验

接地网由多根较长的接地导体相互组合而成，在进行局部接地导体方位探测时主要分为2 种情况：（1）在接地网连接拐点±1.5 m 以外，导体连接拐点处对接地导体探测影响很小可忽略不计，因此可等效为单根接地导体的方位探测；（2）在接地网连接拐点±1.5 m 以内，导体连接拐点处的导体敷设走向可等效为口字形接地导体直角拐点的方位探测。口字形接地导体方位探测图如图5 所示。

图5 口字形接地导体方位探测图Fig.5 Orientation detection diagram of mouth shaped grounding conductor

在进行接地导体方位探测时，分别对单根接地导体和口字形接地导体进行模拟实验，实验场地以单根长为6 m、横截面积为40 mm×4 mm 的镀锌扁钢为实验对象。接地导体方位探测实验测试结果和示意图如图6 所示。

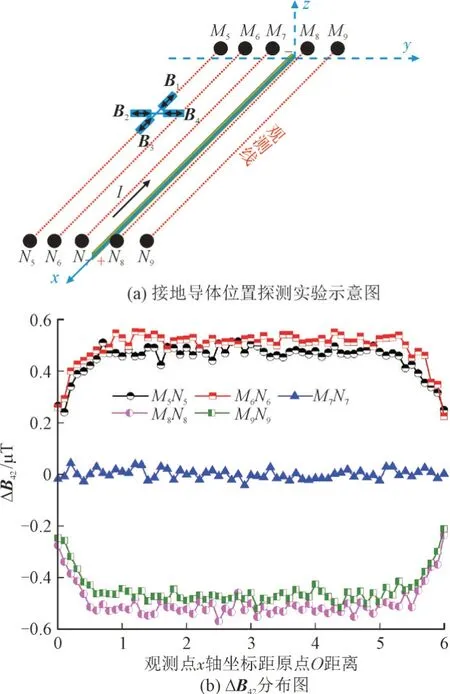
图6 接地导体方位探测实验测试结果和示意图Fig.6 Azimuth detection test results and diagram of grounding conductor

图6（a）中，B1，B2，B3，B4分别为1—4 号传感器位置上的磁感应强度，M5N5－M9N9为观测线段。4 号和2 号传感器所测磁感应强度差值ΔB42分布图如图6（b）所示。在探测区域内沿着同一观测线测量时，若4 号和2 号传感器所测磁感应强度差值ΔB42持续保持在0.4 μT 左右，而1 号和3 号传感器所测磁感应强度基本为0 时，说明在平行于该观测线的下方0.5 m 范围内存在接地导体。具体位置判断方法为：ΔB42＞0 时，接地导体在靠近4 号传感器一侧；ΔB42＜0 时，接地导体在靠近2 号传感器一侧；ΔB42≈0 时，接地导体在观测线的正下方。2 号和4 号传感器探测方式与之同理。在1-4 号传感器配合使用进行接地导体方位探测过程中，1 号和3 号为1 组探测传感器，2 号和4 号为1 组探测传感器。当1 组探测传感器差值变化明显，而另1 组探测传感器差值约为0 时，说明在差值变化明显的这1 组传感器垂直方向有接地导体的存在，沿着该组传感器连线水平方向移动，可知接地导体在磁感应强度测量数值较大的一侧。

M5N5—M9N9观测线段起止点坐标如表2 所示，观测步长为0.1 m。表2 中，M5－M9为观测线起点坐标值，N5－N9为观测线终点坐标值。

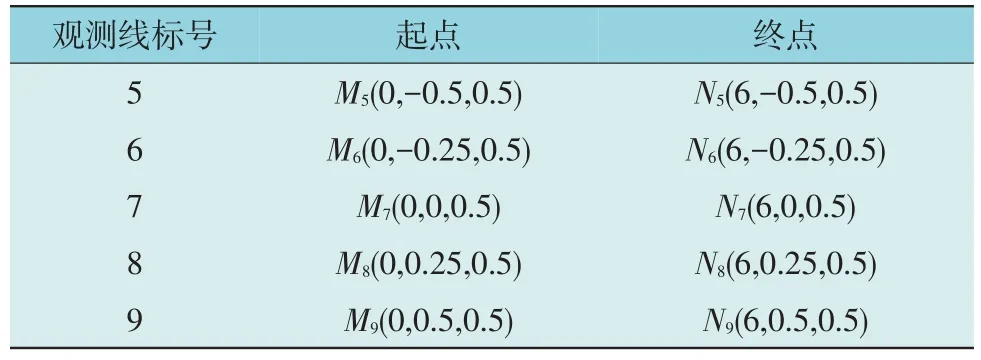
表2 M5 N5－M9 N9观测线段起止点坐标Table 2 M5 N5—M9 N9 observation line coordinates m

图5 中的口字形接地导体与单根接地导体探测区别的关键在于2 根导体连接处附近的探测。口字形接地导体方位探测示意图如图7 所示。

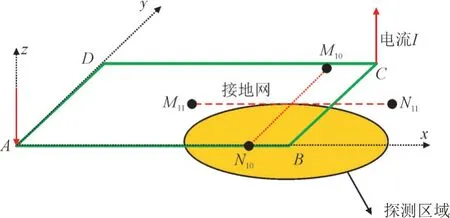
图7 口字形接地导体方位探测示意图Fig.7 Schematic diagram of mouth shaped grounding conductor orientation detection

图7 中，M10和M11分别为观测线起点，N10和N11分别为观测线终点。M10N10和M11N11观测线段起止点坐标如表3 所示。表3 中，观测步长为0.1 m。

表3 M10N10和M11N11观测线段起止点坐标Table 3 M10N10 and M11N11 observation line coordinates m

本文对口字形接地导体连接拐点半径1 m 范围内进行探测。口字形接地导体方位探测磁感应强度差值分布如图8 所示。

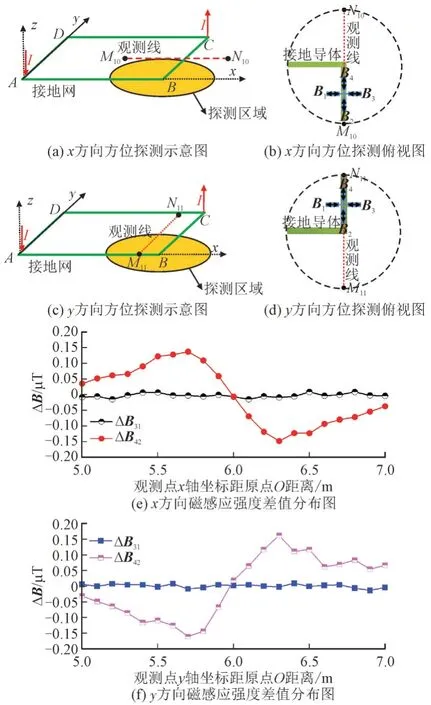
图8 口字形接地导体方位探测磁感应强度差值分布Fig.8 Difference distribution of magnetic induction intensity in orientation detection of mouth shaped grounding conductor

图8 中，观测步长为0.1 m，记录1-4 号传感器所测磁场，并计算3 号和1 号传感器所测磁感应强度ΔB31、4 号和2 号传感器所测磁感应强度差值ΔB42，所得x方向和y方向磁感应强度差值分布图如图8（e）和图8（f）所示。由图8（e）和图8（f）可知，在拐点半径0.5～1 m 范围内，ΔB31和ΔB42差别不大，因此在拐点0.5 m 区域外可等效为单根接地导体的测量；在拐点半径0.5 m 范围内，|ΔB42|明显大于|ΔB31|，探测探头过0 点时磁感应强度差值ΔB42的正负值变化明显（变化幅度高达0.3 μT）且ΔB31约等于0，由此可判定在垂直于观测线方向上存在接地导体，且接地导体连接拐点正好处于ΔB42为0 的观测点正下方。综上，通过配合使用1，2，3，4 号传感器，在拐点半径0.5 m 范围内可有效的判定接地导体连接拐点的位置。

3.2 接地导体深度探测实验

为验证接地导体深度计算方法的可行性，以4根长为6 m、横截面40 mm×4 mm 的镀锌扁钢连接成的口字形接地网为实验对象，观测步长为0.05 m，探测深度为0.4～1 m。M12N12－M15N15观测线段起止点坐标如表4 所示。

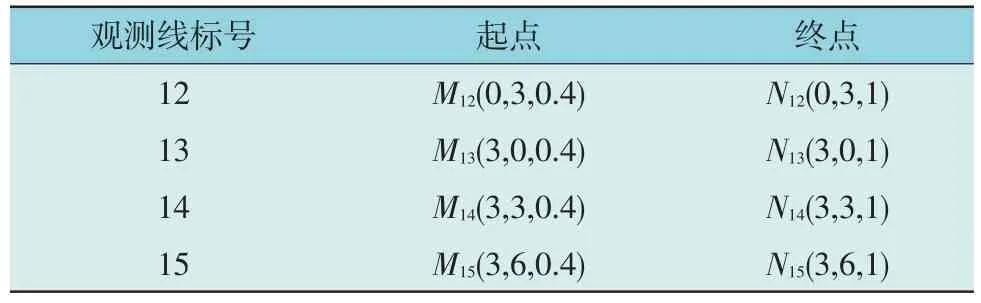
表4 M12N12－M15N15观测线段起止点坐标Table 4 M12N12－M15N15 observation line coordinates m

根据式（4），对观测线段M12N12－M15N15上测量到的磁感应强度值进行计算，口字形接地导体深度计算结果如图9 所示。

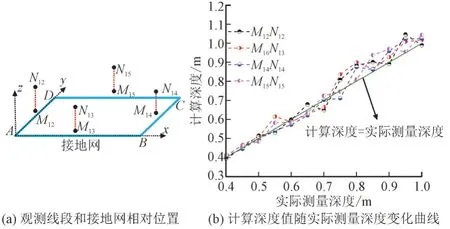
图9 口字形接地导体深度计算结果Fig.9 Calculation results of mouth shaped grounding conductor depth

由图9（b）可知，接地体在0.8 m 及以上深度探测时得到的深度值偏差较大；接地导体在0.4～1 m探测深度范围内得到的深度计算值与实际深度偏差最大为0.096 m。所以在0.4～1 m 探测范围内，本文的深度计算方法可有效的计算接地导体的深度值。

4 结语

本文基于电磁感应原理对电力设备接地网进行定位，提出了一种由6 个HMC1001 传感器组成的阵列式传感探头。所研制探头中，在同一水平面上的1-4 号传感器用于测量接地网水平距离的磁感应强度从而判定接地导体的埋设方位，5 号和6号传感器用于测量接地网垂直距离的磁感应强度从而判定接地导体的深度位置。实验结果证明，本文所提电力设备接地网定位探测方法的可行性与准确性较高，可应用于实际工程。