基于数据驱动的直流输电后续换相失败预判的研究
2022-08-26蔡东阁何思敏
陈 铁,蔡东阁,何思敏,曹 颖
(1.三峡大学电气与新能源学院,湖北宜昌 443002;2.三峡大学(梯级水电站运行与控制湖北省重点实验室),湖北宜昌 443002)
0 引言
高压直流输电系统广泛应用于远距离输电[1-2]。换流站采用12 脉动晶闸管作为换流器件时,极易因交流故障而引发换相失败[3]。首次换相失败通常影响小且可以自行恢复,而后续换相失败危害性较大,可能导致直流系统闭锁,严重威胁电网安全[4-6]。因此,为了能够及时制定和实施保护措施,保证直流输电系统的安全运行,有效进行后续换相失败预判具有重要意义[7-8]。
近年来学者对换相失败的影响因素进行了研究,但针对后续换相失败进行预判和预测的研究较少。文献[9]指出换相失败与换流母线电压、直流电流、越前触发角和过零点相位移有关。文献[10]指出换相失败预测判据的研究应考虑换流母线电压跌落、直流运行工况以及波形畸变等因素。文献[11]提出首次换相失败恢复过程中,换流母线电压、直流电流及触发延迟角的不协调可能导致系统换相能力不足而引发后续换相失败。
文献[12]通过换相失败后的直流电流预判后续换相失败的风险,方法不适用于不对称故障,且未考虑谐波和触发角的影响。文献[13]提出了基于换相电压时间面积的后续换相失败风险指标,忽略了非对称故障下电压畸变造成的影响。文献[14]采用临界电压预判连续换相失败的风险,忽略了故障下换相过程中触发角和交流电压的波形畸变,对直流电流上升幅度较大的情况预判结果误差较大。文献[15]基于触发角偏差量预判换相失败,忽略了故障下换相过程中交流电压和直流电流的变化。
换相过程与直流电流、触发角指令、换流母线电压等多个因素关系密切,但现有的方法对其恢复过程均做了一定程度的简化等效,削弱了模型的准确性和适用性。同时,这些方法都要精确计算换相电抗,多馈入直流输电受端交流系统结构及运行方式复杂,在受端发生短路故障的情况下,换相电抗的计算精度不够。
极限学习机[16](Extreme Learning Machine,ELM)是一种前馈神经网络,在暂态预测上有较好的性能,具有泛化性能好、训练参数少、学习速度快的优点。目前,ELM 已经应用在电力系统暂态稳定评估[17]、输电线路故障检测[18]、电力系统电压暂降源辨识[19]等方面。
本文将ELM 分类理论引入换相失败预判领域,提出了一种基于数据驱动的后续换相失败预判方法。采集首次换相失败后逆变侧换流母线电压、直流电流、触发延迟角数据,通过计算得到直流电流最大值、平均值、最小值等11 个特征作为ELM 分类器的输入,以后续换相失败信息作为输出,构建后续换相失败预判模型。利用电力系统电磁暂态仿真程序(Power System Computer Aided Design/Electro-Magnetic Transient Program for DC,PSCAD/EMTDC)建立高压直流输电模型,通过故障仿真获得大量数据样本,对模型进行训练和测试。结果表明,模型预判的准确率为88.33%,可对后续换相失败进行有效预判。
1 后续换相失败分析及特征
1.1 后续换相失败机理分析
关断角γ是决定能否成功换相的根本原因。当γ小于极限关断角γmin(频率为50 Hz 的工频条件下所对应的γmin=7°)时,将发生换相失败[20]。
根据换相电压积分面积理论,当系统能够提供的最大叠弧面积提供量不小于叠弧面积需求量时,换相成功,表达式为[20]:
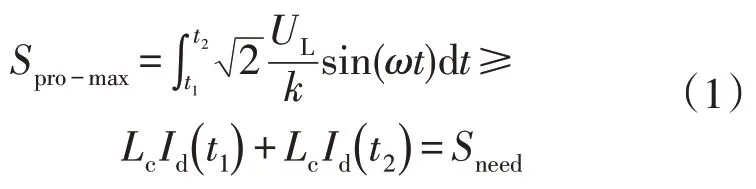
式中:Sneed为保证成功换相的叠弧面积需求量;Spro-max为系统能够提供的最大叠弧面积提供量;t1为触发时刻,对应于触发延迟角α;t2为叠弧面积提供量最大的时刻,对应于极限关断角γmin;ω为角频率;UL为逆变侧换流母线电压有效值;k为换流变压器变比;LC为系统等效换相电抗;Id(t1)为t1时刻的直流电流值;Id(t2)为t2时刻的直流电流值。
叠弧面积需求量由换相电抗和直流电流决定;最大叠弧面积提供量由逆变侧换流母线电压、触发延迟角、换流变压器变比决定。另外,换流母线电压波形畸变也会影响叠弧面积提供量。换流变压器变比和换相电抗均为系统结构参数,可不予以考虑。
1.2 特征指标
将恢复过程中重要的电气量和控制量作为特征指标进行后续换相失败预判。
首次换相失败后,逆变侧换流母线电压恢复较慢,处于较低水平或者出现二次跌落,均会使最大叠弧面积提供量明显减小,带来后续换相失败风险[21-22]。同时,直流电流恢复过快或再次超过稳态值,完成换相所需要的叠弧面积需求量也随之增大,若最大叠弧面积提供量不能满足需求量,将引发后续换相失败[11,23]。采用恢复过程中逆变侧换流母线电压有效值的最大值、最小值和平均值,直流电流的最大值、最小值和平均值及采样间隔作为特征指标表征逆变侧换流母线电压和直流电流的恢复过程。
交流不对称故障发生后,导致换流母线电压产生畸变,引起电压幅值下降和相位角φ前移,使叠弧面积提供量减小,即使直流电流、换流母线电压幅值都恢复到稳定值左右,也可能由波形畸变使得最大叠弧面积提供量不能满足需求量,引发后续换相失败[24]。
将故障后的逆变侧换流母线电压谐波电压总畸变率作为特征量,衡量电压波畸变程度,见式(2)—式(3)。

式中:THD,A,THD,B,THD,C分别为A,B,C 三相的电压波形畸变率;THD,u为谐波电压总畸变率;U1为基波电压有效值;Un为第n次谐波电压有效值。
换相失败后,直流控制系统会提前触发减小触发延迟角,增大最大叠弧面积提供量,促进换相[22]。将触发延迟角的最大值、最小值和平均值作为特征指标预判后续换相失败。
2 极限学习机基本原理
ELM 网络结构如图1 所示。

图1 ELM网络结构图Fig.1 ELM network structure diagram
对于N个不同的样本,其中,Xi=[xi1,xi2,…,xin]T∈Rn为第i个样本的输入特征;Yi=[yi1,yi2,…,yim]T∈Rm为第i个输入样本所对应的输出结果;Rn为所有样本的输入特征集合;Rm为对应的所有样本的输出结果集合;m,n分别为输出层节点数和输入层节点数;则ELM 数学模型[16]可表示为:
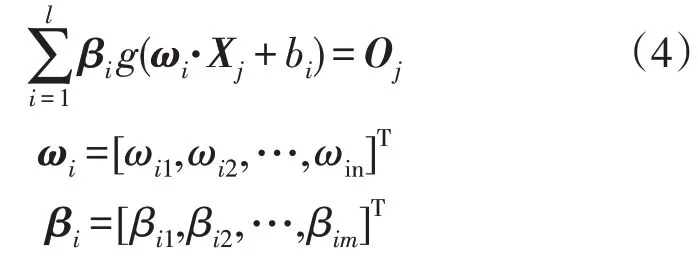
式中:l为隐含层节点数;g(·)为隐含层的激活函数;bi为第i个隐含层节点的阈值;ωi为连接第i个隐含层节点和输入节点的权重向量;βi为连接第i个隐含层节点和输出节点的权重向量;ωi·Xj为ωi和Xj的内积。
参考文献[16],激活函数为g(·)的l个隐含层节点的ELM 网络可以零误差逼近这N个样本,可表示为:
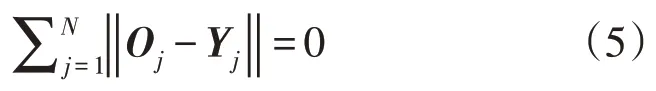
即,存在合适的βi,ωi和bi,使得
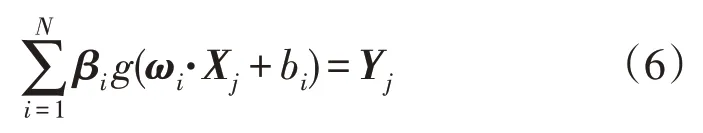
式(6)N个方程可以简写为:

其中,
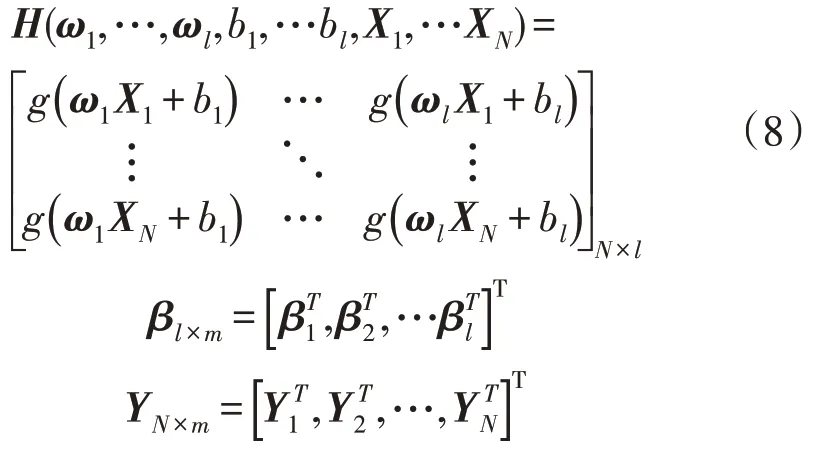
式中:H为隐含层输出矩阵;βl×m为输出权值矩阵;YN×m为目标输出矩阵。
ELM 网络的学习过程可看成一个非线性优化问题,当输入层权值和隐含层偏置随机产生被确定后,只需要求解出输出层的权值保证训练误差最小即可,其最优解为[16,25]:

式中:H+为隐含层输出矩阵H的Moore-Penrose广义逆矩阵,可用奇异分解法进行求解。
3 后续换相失败预判
数据驱动后续换相失败预判策略如图2 所示。
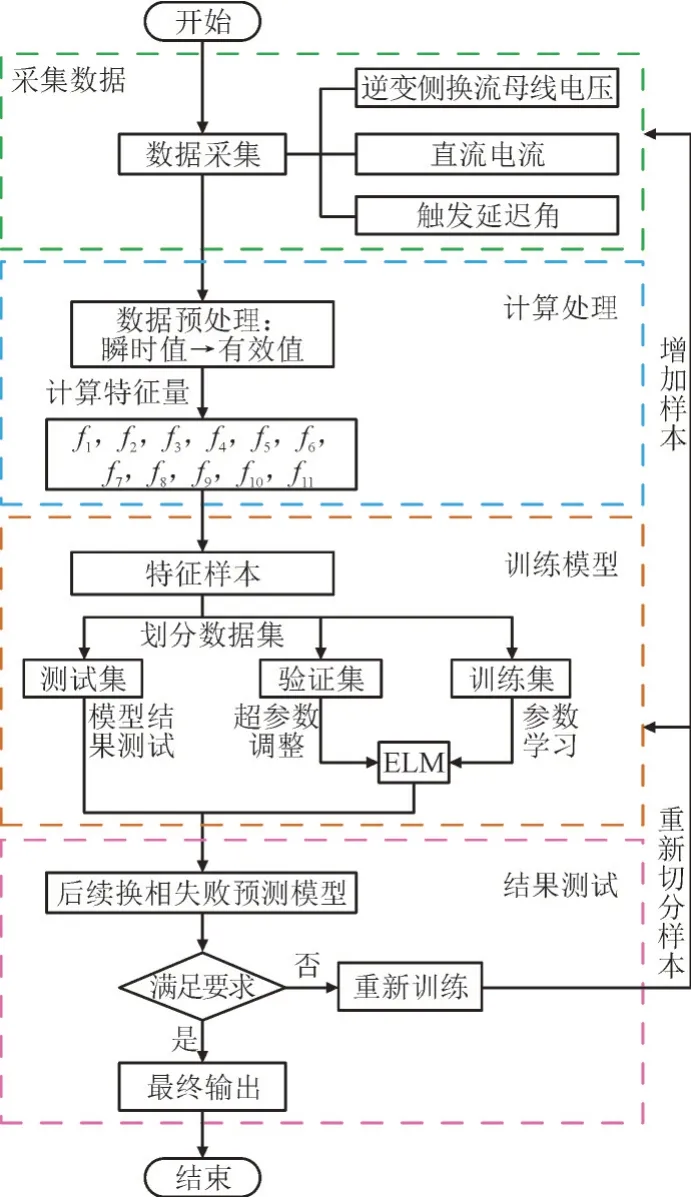
图2 数据驱动后续换相失败预测方法Fig.2 Data driven prediction method for subsequent commutation failure
具体实现过程如下:
1)采集首次换相失败后的逆变侧换流母线电压、直流电流、逆变侧触发延迟角作为原始数据样本集。首次换相失败的判定和采集时间通过捕捉关断角进行确定[12,26-28],当首次捕捉到实际关断角小于极限关断角时,确定首次换相失败发生,当捕捉到关断角恢复到参考值时,开始采集数据,捕捉到关断角再次降到参考值时,停止数据采集。其中,逆变侧换流母线电压需要进行2 次不同起始时间的采集,另一次的采集起始于故障发生时刻,终止于关断角降为参考值时刻。采样间隔为0.000 2 s。
2)将1)中采集的数据通过计算处理转化为特征量,其中,需要将开始于关断角恢复到参考值时间时刻采集的逆变侧换流母线电压计算成有效值,具体特征量如表1 所示。

表1 输入特征量Table 1 Input feature vector
3)将2)中特征集按照6:2:2 划分为训练集、验证集及测试集,以训练集和验证集对后续换相失败模型进行训练,具体训练步骤为:(1)选择满足无限可微的函数g(·)作为隐含层节点的激活函数,选取不同的函数作为激活函数,进行训练集和验证集准确率的对比,选出适用于后续换相失败预判的激活函数;(2)在激活函数确定后,对比不同隐含层节点数的训练集和验证集的准确率,选出适用于后续换相失败预判的隐含层节点数;模型训练完成。这时利用训练好的模型便可完成对测试数据的预测测试。
4)训练好的模型输入变量由换流母线电压、直流电流、触发延迟角等特征因素构成,输出变量为后续换相失败信息标签时,则可对模型进行结果测试。
采用分类准确率(Classification Accuracy,CA)(量值为AC)进行模型结果的测试。计算公式为[19]:

式中:对于给定的测试集,TP,TN分别为正类判定为正类和负类判定为负类的样本数;P,N分别为正类和负类的总样本数。
用测试集对模型的训练结果进行仿真测试,当结果达到预想效果时,将训练好的模型用于对后续换相失败预判;当效果不佳时,再增加样本或者重新切分样本集重新优选ELM 网络的输入参数,训练ELM 后续换相失败预判模型。
4 仿真验证
在PSCAD/EMTDC 电磁暂态仿真软件中,以IEEE 39 节点标准系统中增加4 回直流,构成如图3所示的仿真模型。其中,A,B,C,D 为4 回直流输电系统。直流输电系统均采用Cigre 标准模型,相关参数设置为:直流额定功率均为1 000 MW;直流额定电压均为500 kV;逆变侧关断角参数均为15°。
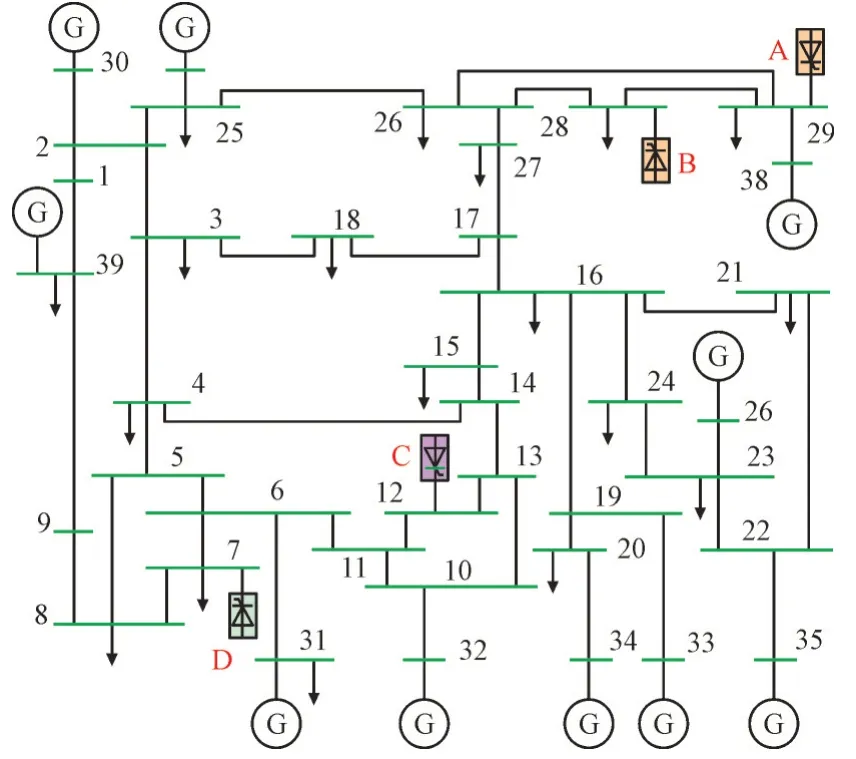
图3 含直流的IEEE 39节点修改系统Fig.3 IEEE 39 node modification system with DC
通过在逆变侧交流系统不同节点母线设置不同故障生成所需数据样本。故障相关参数如表2所示。
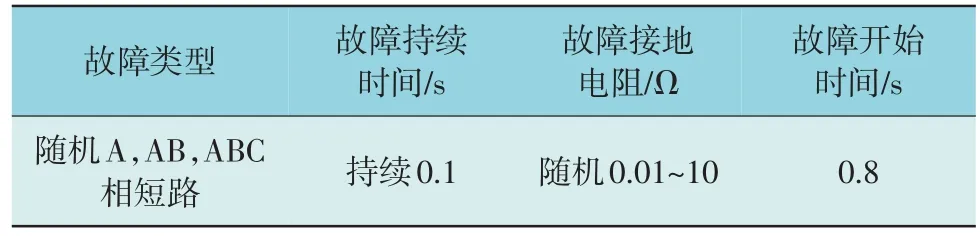
表2 故障设置相关参数Table 2 Fault setting related parameters
本文算例中用于分类预判的总样本数为1 200 个,不发生后续换相失败样本数为600 个,发生后续换相失败样本数为600 个。进行仿真测试时,不发生后续换相失败的类别标签为1,发生后续换相失败的类别标签为2。
4.1 ELM激活函数的优选
不同激励函数下的准确率对比如图4 所示。以训练集和验证集作为ELM 算法的输入,选取隐含层节点数为10—60,通过比较不同激活函数训练集和验证集的准确率进行激活函数的优选,所选取激活函数分别为:S 型函数(Sig)、正弦函数(Sin)和硬阈值函数(Hardlim)。
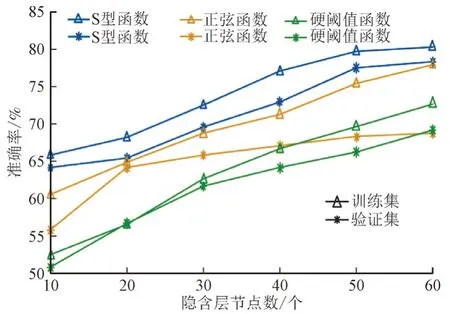
图4 不同激励函数下的准确率对比Fig.4 Comparison of accuracy under different excitation functions
由图4 可知,通过对不同激活函数的模型准确率对比,激活函数不同,模型准确率不同,激活函数为S 型函数时模型准确率最高,训练集准确率最高达80.28%,验证集准确率最高达到78.33%。因此,选择S 型函数对换相失败数据进行分析。
4.2 ELM隐含层节点数的优选
不同隐含层节点数下准确率对比如图5 所示。选取激活函数为S 型函数,进一步对比不同隐含层节点数的模型准确率。
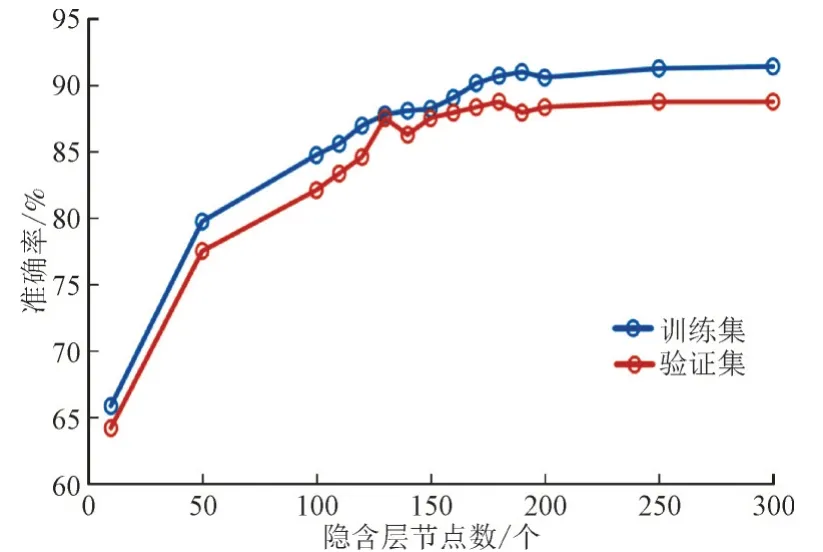
图5 不同隐含层节点数下准确率对比Fig.5 Comparison of accuracy under different nodes of hidden layer
由图5 可知,模型准确率受隐含层节点数影响,当隐含层节点数在0—50 之间,模型准确率急剧上升,训练集的准确率上升了13.89%,验证集的准确率上升了13.33%;当隐含层节点数在50—180 之间,模型准确率上升趋势有所变缓,训练集的准确率上升了10.97%,验证集的准确率上升了11.25%;当隐含层节点数在180—300 之间,模型准确率趋于平稳,训练集的准确率上升了0.7%,而验证集的准确率在隐含层节点为180 时达到了最高值88.75%且不再上升。即在隐含层节点数为180 之后再继续增加隐含层节点数不仅对提高准确率关系不大,反而会加大模型复杂度,增大运算量。因此,选择隐含层节点数为180 对换相失败数据进行分析。
4.3 预测结果
选择仅考虑换流母线电压幅值作为特征指标[29-31],选择直流电流和换流母线电压作为特征指标与本文特征指标进行对比分析,具体的分类结果如图6—8 所示。

图6 电压因素测试集的实际分类和预测结果(准确率80%)Fig.6 Actual classification and prediction results of voltage factor test set(accuracy 80%)
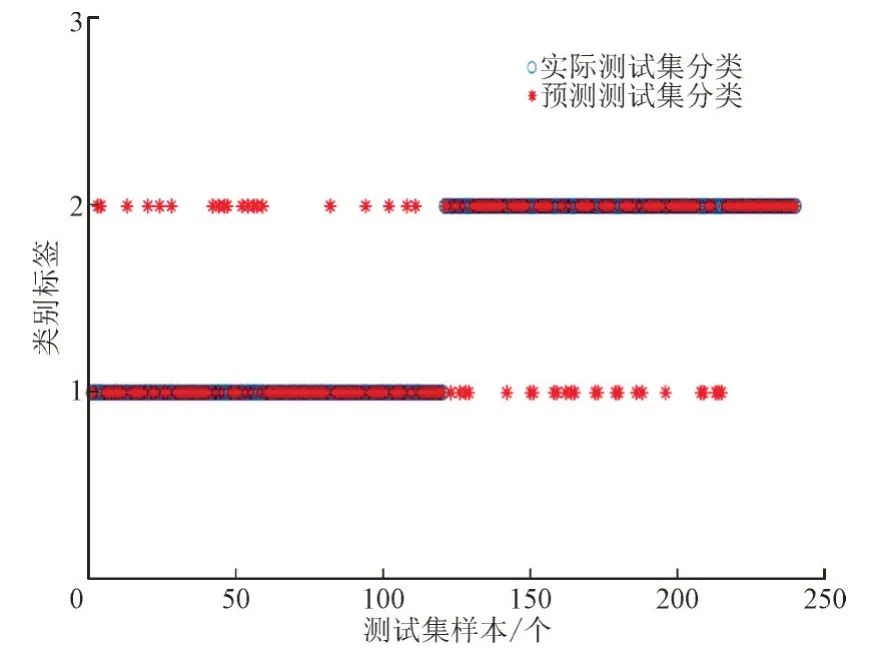
图7 电压、电流因素测试集的实际分类和预测结果(准确率81.67%)Fig.7 Actual classification and prediction result of voltage and current factor test set(accuracy 81.67%)
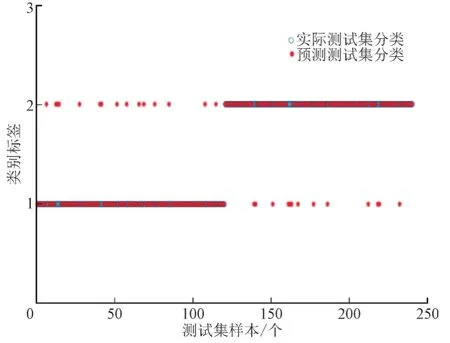
图8 多因素测试集的实际分类和预测结果图(准确率88.33%)Fig.8 Actual classification and prediction results of multi-factor test sets(accuracy 88.33%)
综上所述,经过仿真测试结果的验证,本文提出的模型准确率可达到88.33%,而只考虑单一交流电压因素和考虑交流电压、直流电流因素的模型准确率分别为80%和81.67%,证明了所提方法的可行性和有效性。
5 结论
针对后续换相失败影响因素复杂且主导因素具有随机性的问题,提出一种基于数据驱动的后续换相失败预判方法,通过仿真测试得出了以下结论:
1)本文在考虑多因素的基础上,提出的后续换相失败预判方法,相较于对恢复过程做了简化等效的方法,具有更高的准确率。
2)相比于对后续换相失败风险等级进行预判,本文所提方法能够对后续换相失败进行预判,而不是进行概率预判。
3)对比于现有对后续换相失败的预判方法,本文所提方法不需要对故障下进行换相电抗的计算并适合所有短路故障,对场景的适应能力强。
