基于双层随机规划的电力零售商短期决策模型

赵文杰，杨 萌，刘军会，邓振立，何雯雯

（1.国网河南省电力公司经济技术研究院，河南郑州 450000；2.西安交通大学电气工程学院，陕西西安 710054）

0 引言

对电力零售市场的开放促进了电力市场的自由化、竞争力和创新力。在放松管制的地区，终端用户零售客户有权选择其电力供应商，以更好地满足其电价偏好和服务需求[1]。至今，已经有超过25个欧盟国家和13 个亚太地区国家完全解除了市场管制[2]。如今，我国的电力市场建立了批发-零售两级市场机制，为电力零售商的报价决策带来了新的挑战[3-4]。根据国家统计局数据，截至2021 年7 月，以2019 年7 月为基期，风电发电量增长25.4%；太阳能发电量增长12.1%[5]。分布式可再生能源（Distributed Renewable Energy，DRE）是未来电力发展的必然选择[6]。但以光伏为代表的DRE 发电具有随机性、波动性、间歇性等特点[7]，为了尽可能降低这些不确定因素带来的负面影响，电力市场的风险管理成为近年来热门研究课题[3]。

在目前的电力零售市场中，现有的DRE 市场缺乏成熟的业务模式和交易机制，加上分布式系统的感知能力有限，使得DRE 市场对于许多电力零售商和负荷服务商“不可见”[1]。大多数文献只考虑了零售客户参与需求响应计划[8-9]。文献[10]提出要建立完善的辅助市场机制、价格机制，通过利用绿色证书交易来实现DRE 的优化配置。文献[11]提出将DRE 市场的保障性消纳纳入电力市场的机制。文献[12]提出要结合国家政策以及要考虑我国可再生能源发展中存在的问题，以重点计划项目为主以财税价格政策为辅推动DRE 的快速发展。文献[13]提出引入电力保险来转移可再生能源出力不确定性所导致的收益风险。文献[14]提出要考虑用户的策略行为，以用户效益为首要目标制定零售电价套餐。文献[15]考虑了电力用户的特点及需求影响，构建了用户、零售商及不同类型发电厂的电力模型。

综上，目前文献在模拟DRE 生产商和电力零售商的互动模型时只考虑了DRE 生产商之间的竞争，而没有考虑过零售层面的自由DRE 市场对电力零售商短期决策模型的影响。在此基础上，本文提出了一种基于双层随机规划的电力零售商短期决策模型，首先阐述了分布式可再生能源市场及双层随机规划模型框架，随后将双层随机规划模型转化为等效的单层混合整数线性模型，在此基础上考虑了日前市场和实时市场的电价、分DRE 产量、电力需求和电力零售商与其它负荷服务商（Load Serving Entities，LSEs）报价的随机性，最后，通过实例分析验证了该模型的有效性。

1 双层随机规划模型

1.1 DRE市场及双层模型框架

DRE 市场框架如图1 所示。在该框架下，DRE生产商可以将其剩余的能源直接出售给LSEs，其中包括正在商谈的电力零售商（以下简称电力零售商）及LSEs。LSEs 向DRE 生产商发送DRE 接下来1 d 每个时间段t的报价。另一方面，DRE 生产商对收到的所有价格做出反应，并确定向每个LSE供应DRE 的百分比。在拟议的框架内，假设所有LSEs 都提供了智能电网技术和交易平台，使LSEs之间能够安全高效地交互。

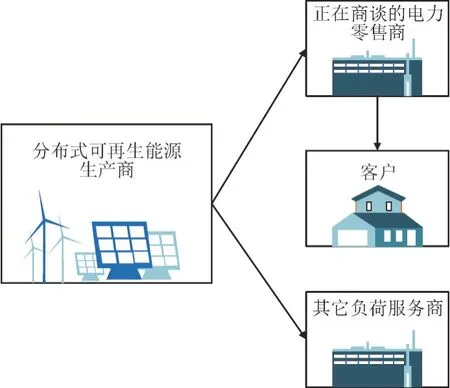
图1 分布式可再生能源市场框架Fig.1 DRE market framework

电力零售商和DRE 生产商的双层决策框架如图2 所示。上层的电力零售商在2 个阶段中最小化其期望采购成本。在第1 阶段中，电力零售商定义了日前市场的最优报价曲线，以及在没有日前和实时市场价格、DRE 产量、电力需求和DRE 份额信息的情况下，下一个工作日的每个时段DRE 报价。第一阶段的决策也称为此时此地决策，因为它们是在已知随机变量[16-19]之前做出的。接下来的运营日里，在日前市场出清以及DRE 产量、电力需求和DRE 份额已知后，电力零售商决策其在第二阶段的每个时间段参与实时市场的程度。第2 阶段的决策也被称为观望决策，因为它们是在已知随机变量后做出的。需要注意的是，实时市场，也称为平衡市场，是电力零售商修正其第一阶段电力偏差以确保能量供需平衡的平台。处于下层的DRE 生产者通过确定DRE 的百分比（即DRE 份额），以最大限度地提高他们的总收入。

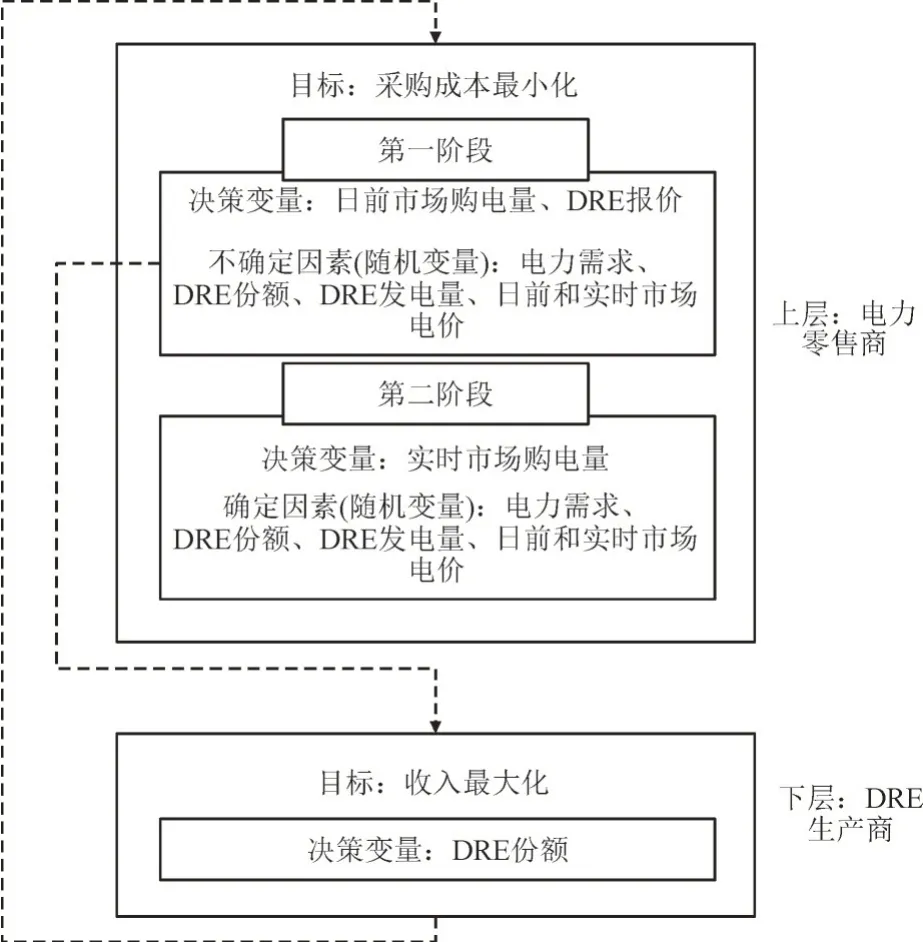
图2 双层决策模型框架Fig.2 Bilevel modeling framework

1.2 双层随机规划数学模型

将电力零售商的决策模型描述为双层随机规划问题。

对于上层模型，以电力零售商采购成本最小化为优化目标，上层问题的目标函数由2 部分构成：第1 部分为电力零售商在日前市场、实时市场和分布式可再生能源市场获取的预期采购成本；第2 部分为乘以一个权重因子的条件风险值[20-22]（Conditional Value at Risk，CVaR）。构建的目标函数如下：

1.2.1 上层问题的约束条件

电力零售商购买电力能源的平衡约束：

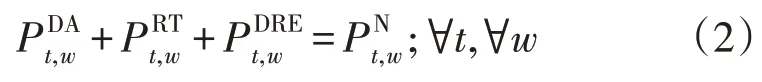
电力零售商购买DRE 电力最小量以及所需DRE 电力有如下约束：

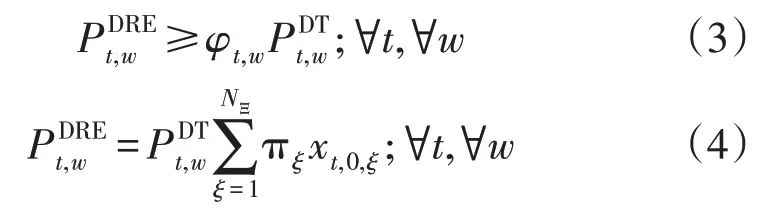
式中：φt,w为电力零售商在时间t和场景w中设定的最小DRE 购买百分比；ξ为下层问题中的不同场景，每一个场景ξ都代表了一个下层不确定性的组合，πξ为场景ξ的概率，且∑πξ=1；NΞ为场景ξ的总数；为时间t和场景w内并入本地电网的DRE 总量；xt,0,ξ为在时间t和场景ξ内出售给电力零售商的DRE 份额。

式（5）为日前市场的非预期性约束，式（6）定义了日前市场的递减供给曲线：

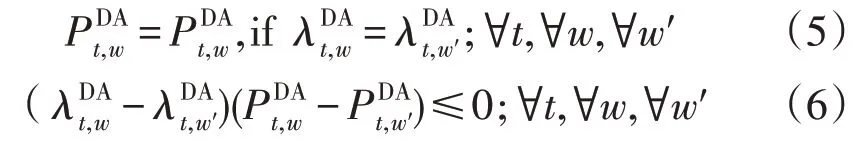
式中：w′为上层问题中不同场景。

式（7）用于计算每个场景w的CVaR，即：

式（8）为非负变量声明，即：

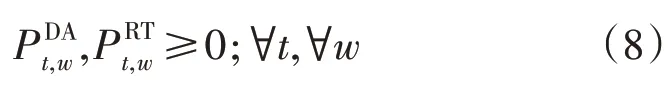
对于下层模型，以DRE 生产商的收入最大化为优化目标，构建的目标函数如：

1.2.2 下层问题的约束条件

出售给电力零售商和LSEs 的DRE 份额约束，即：

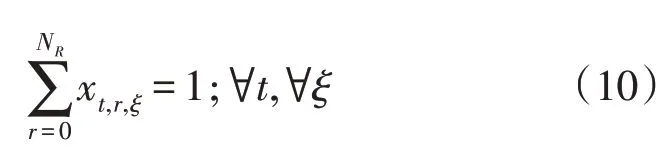
其中出售量均非负，即：

1.3 等效混合整数线性规划模型

下层问题的目标函数可写作：

下层问题式（9）—式（11）的拉格朗日对偶函数为：

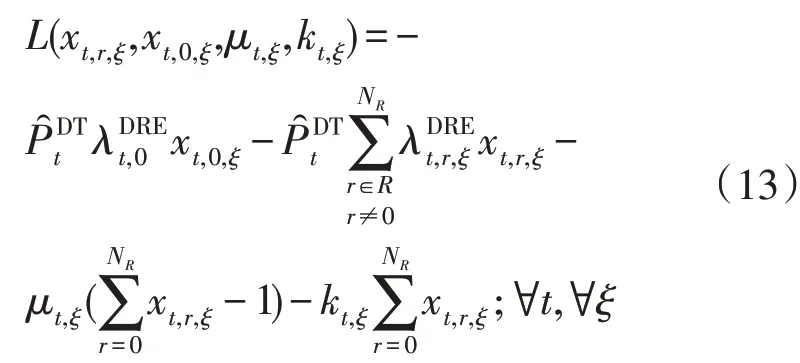
式中：μt,ξ和kt,ξ为拉格朗日乘子。

下层问题式（9）—式（11）的KKT 条件包括：

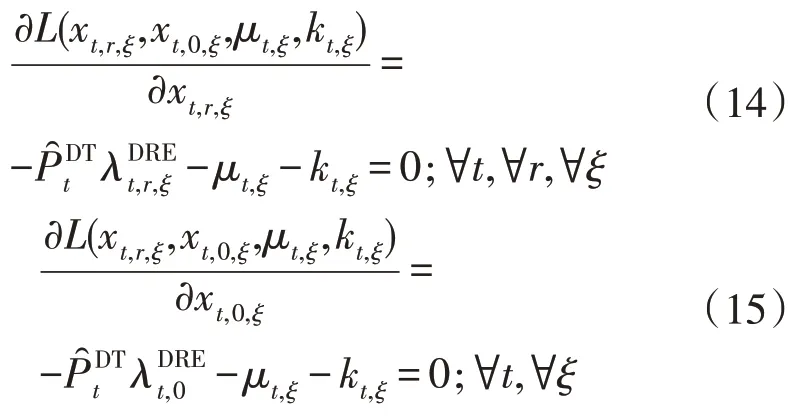
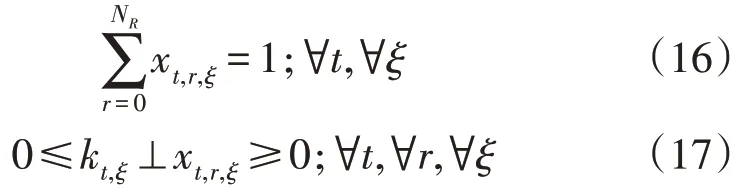
结合式（13）—式（15）可得：

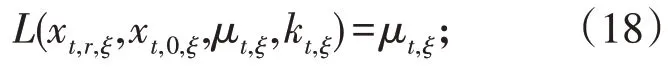
式（17）可通过大M 法[24]等效线性化，得：

结合式（19）—式（21），式（14）—式（17）可写作：

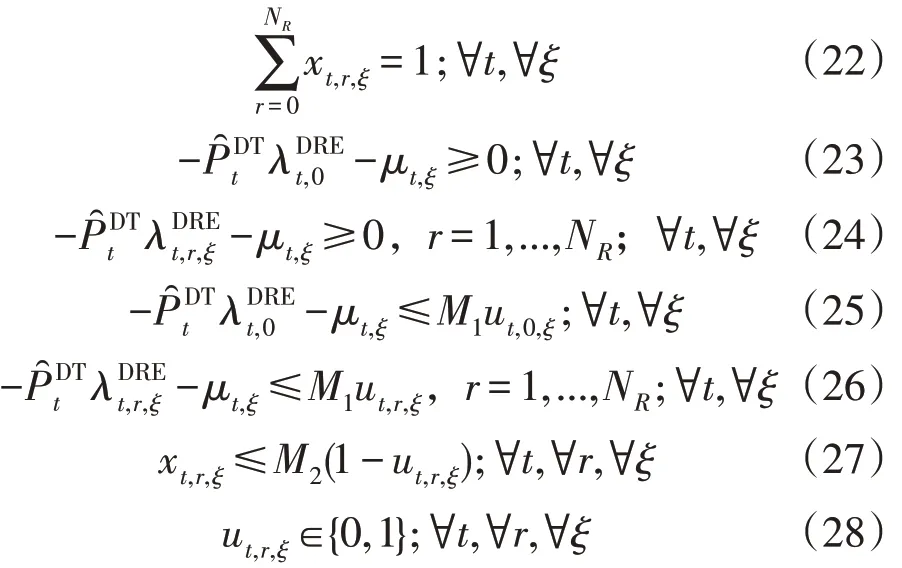
式中：M1，M2为惩罚因子；ut,r,ξ为布局变量。

需要注意的是，式（25）—式（27）中M1和M2为惩罚因子，且应当为充分大的正数，但取值也不能过大，否则容易引起计算误差[17]。

下层模型的对偶问题优化目标函数为：

根据强对偶理论，可得：

重新排列式（30）可得：

结合式（4）和式（31）可得：

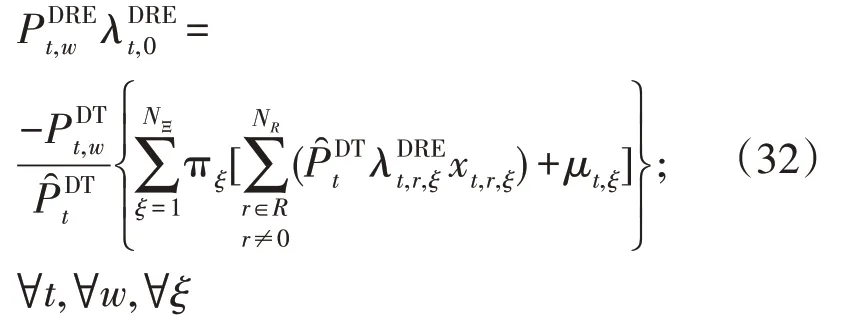
等效的MILP 模型目标函数为：

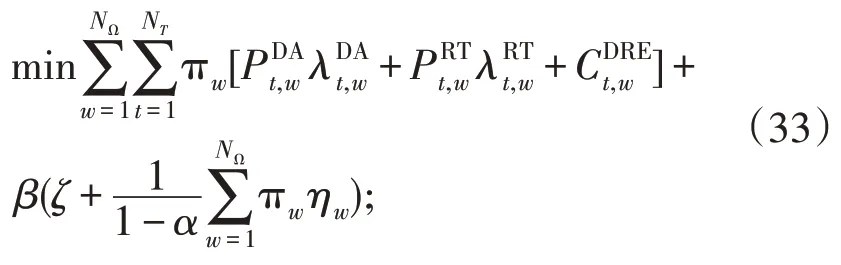
2 算例分析

2.1 算例参数

美国的电力市场运行相对平稳，交易机制较为完善，被世界上大多数国家认可[25]，研究美国电力市场对我国电力市场的建设有着积极的借鉴作用，本文收集美国电力市场历史电价数据进行分析。由于春季光伏产量丰富的时间主要为日间，故本文分析的电力市场运营时间为9:00 到18:00，在这10 h中，电力零售商和LSEs 可参与DRE 市场。此外，每个时段t对应1 h。本文通过2 个算例证实了所提模型的有效性。在算例1 中，每个时间段内的电力零售商与LSEs 关于DRE 报价的期望值与日前和实时市场价格的期望值几乎相同，且对应的标准偏差低于实时市场价格。在算例2 中，每个时间段内的电力零售商市场和LSEs 关于DRE 报价的期望值都高于日前和实时市场价格的期望值，且标准偏差低于实时市场价格。

2 个算例中电力零售商的净功率需求与并入本地电网的DRE 电力如表1 和表2 所示。

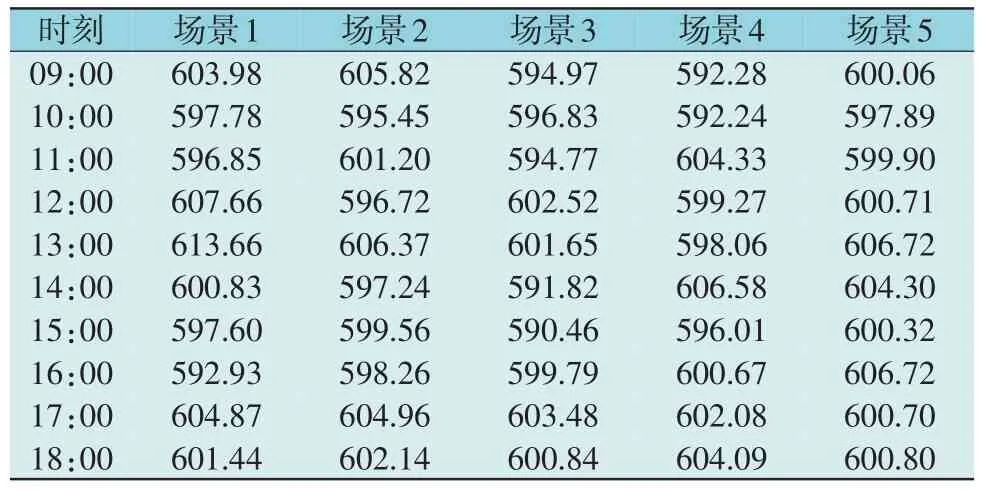
表1 净功率需求Table 1 Net power demand MW

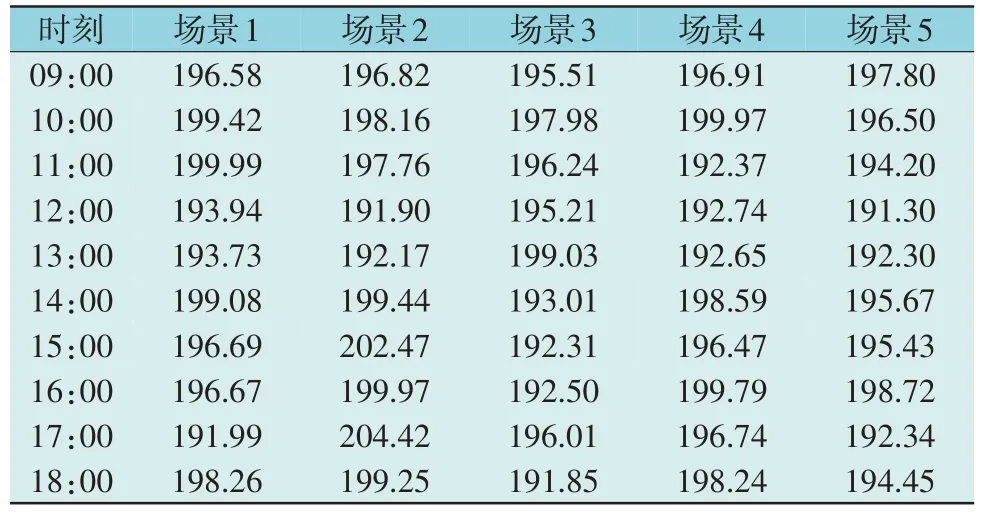
表2 并入本地电网的DRE电力Table 2 Total DRE integrated into local grid MW

2 个算例都采用Yalmip 语言进行建模，并使用Matlab R2018b 的Cplex 进行求解。

2.2 算例1及结果分析

算例1 中，日前市场、实时市场与电力零售商和LSEs 关于DRE 报价的期望值与标准偏差如表3所示。且在算例1 中，没有最小的DRE 购买量约束，即：φt，w=0。

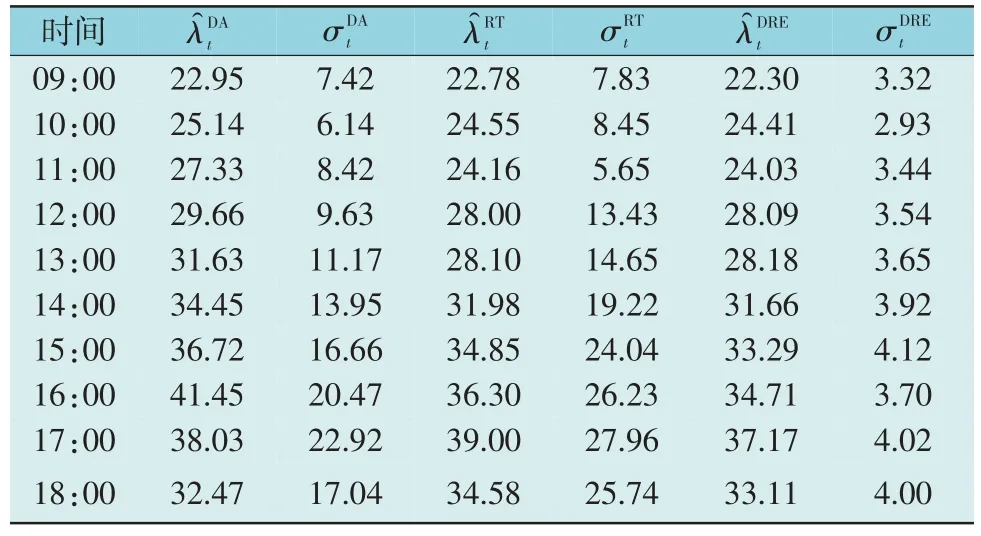
表3 日前市场、实时市场和电力零售商价格场景的期望值和标准值Table 3 Expected values and standard deviations of dayahead market，real-time market and electricity retailer[$·（MWh）-1]

最初，假设电力零售商是一个风险中立者，即：β=0。

图3 比较了电力零售商参与整个电力批发市场（日前市场和实时市场）的采购成本与参与电力批发市场和DRE 市场的采购成本。

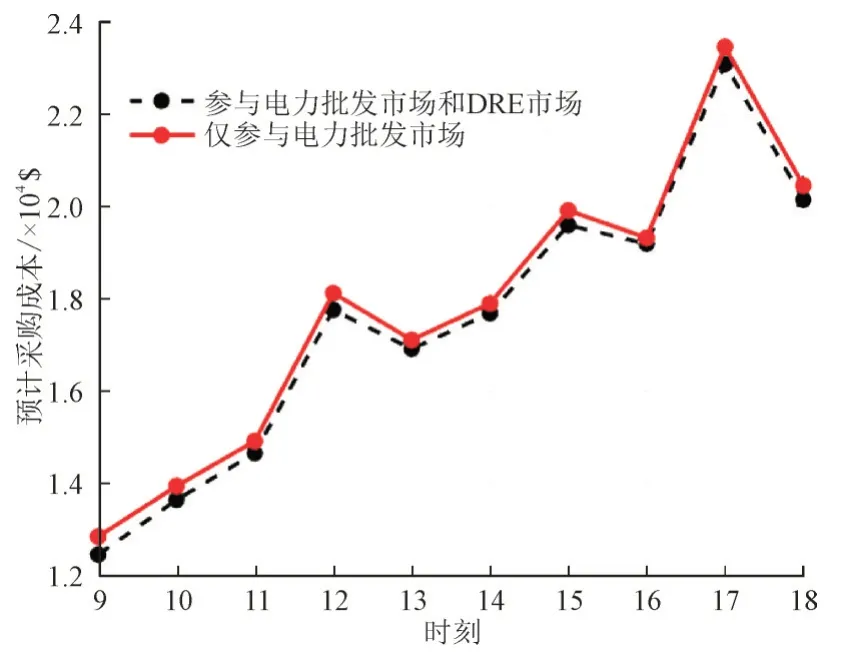
图3 电力零售商的预期采购成本Fig.3 Expected purchase cost of electricity retailer

图4 展示了电力零售商参与DRE 市场的每小时成本降低情况。

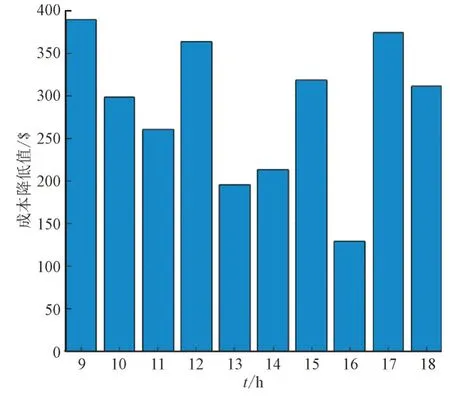
图4 零售商参与DRE市场后的采购成本降低值Fig.4 Hourly cost reduction of the retailer from participating in DRE market

图3 和图4 的结果表明，电力零售商通过参与DRE 市场可以在一定程度上降低成本。

为了分析风险厌恶对电力零售商决策和期望成本的影响，将单位置信水平α设置为0.95，风险厌恶参数β的取值范围为0～10，为了便于在曲线图中展示电力零售商从风险中立到风险厌恶变化的差异，故在算例分析中，所取的β值为0，1，3，5，8和10。

图5 展示了电力零售商总的预期采购成本Cexp和CVaR 值的曲线关系。

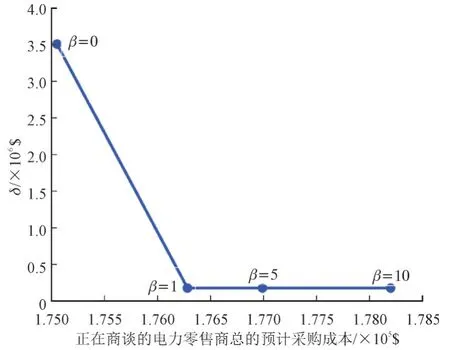
图5 不同β值下零售商的总期望成本和CVaRFig.5 Total expected cost and CVaR of the retailer for different values of β

图5 中，不同β表体所对应的CVaR 值与电力零售商总的预期采购成本关系如表4 所示。

表4 不同β 所对应的CVaR值与电力零售商总的预期采购成本Table 4 Total expected purchace cost of the retailer and CVaR for different values of β×106$

图5 的曲线说明风险中立条件下，电力零售商的期望采购成本更低，但CVaR 值更高；风险厌恶条件下，电力零售商的期望采购成本更高，但CVaR 值更低。因此，电力零售商应该自行权衡预期利润和CVaR。

图6 展示了风险管理对电力零售商13：00 时DRE 报价的影响。

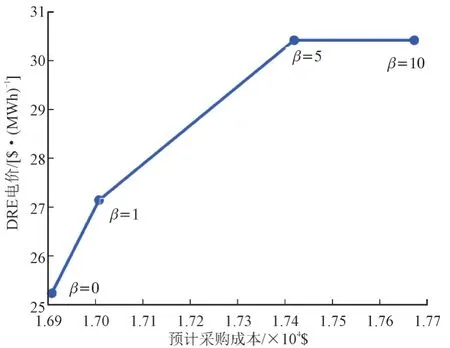
图6 不同β 值下电力零售商的DRE报价与13：00时预期采购成本Fig.6 DRE price bids of the retailer versus the expected cost at 13:00 for different values of β

图6 的曲线说明电力零售商的风险厌恶程度越高，其DRE 报价也越高，此举措是为了在DRE 市场上购买更多的电力能源，以应对不稳定电力池的价格波动影响。

图7 展示了风险管理对于电力零售商在13：00日前市场报价的影响。

图7 不同β 值下电力零售商在13：00时的日前市场曲线Fig.7 Day-ahead market curves generated by the retailer at 13:00 for different values of β

图7 的曲线说明风险中立条件下，电力零售商更加愿意在日前市场价格较低时购买尽可能多的电力能源，以避免DRE 市场电价波动的影响；另一方面，风险厌恶条件下，电力零售商则比较愿意在日前市场价格较低时少量购买日前市场的电力能源，剩余所需能源则在DRE 市场购买，其原因在于DRE 市场的价格波动较低。

2.3 算例2及结果分析

算例2 中，日前市场、实时市场与电力零售商和其它负荷服务商DRE 报价的期望值与标准偏差如表5 所示。

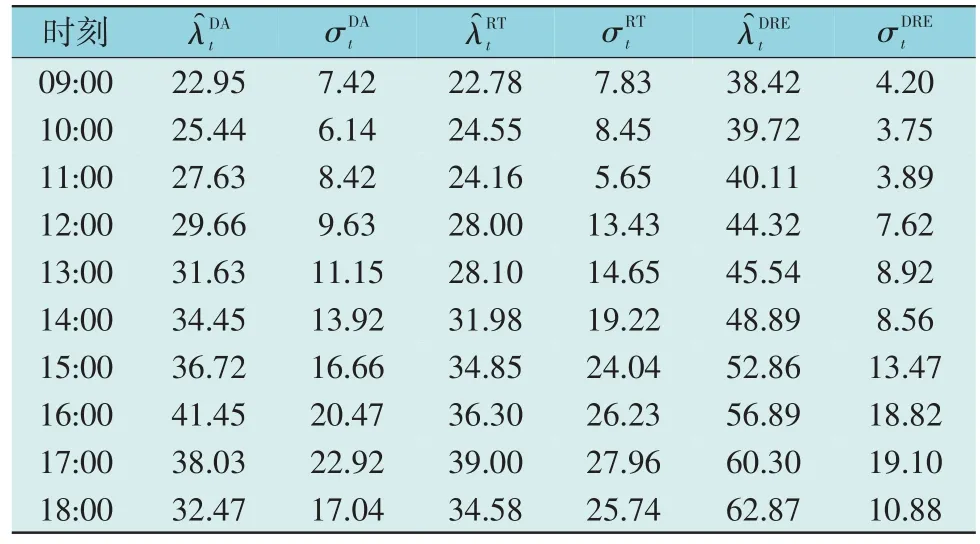
表5 日前市场、实时市场和电力零售商价格场景的期望值和标准值Table 5 Expected values and standard deviations of dayahead market，real-time market and electricity retailer[$·（MWh）-1]

为了分析不同φt,w（DRE 最小购买量）取值对正在商谈的电力零售商决策和期望成本的影响，将置信水平α设置为0.95，风险厌恶参数β设置为1，φt,w取值为0～1。

图8 展示了电力零售商在不同φt,w的情况下的DRE 报价曲线。

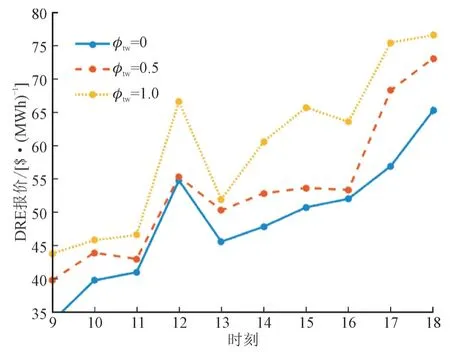
图8 不同φt,w 值下电力零售商的DRE报价Fig.8 DRE price bids of the retailer for different values of φt,w

图8 的曲线说明在同一时间段t内，φt,w当的值较低时，电力零售商的DRE 报价也较低；当φt,w的值较高时，电力零售商的DRE 报价也较高。

图9 展示了在不同φt,w值的情况下，电力零售商在日前市场13：00 时的供给曲线图。

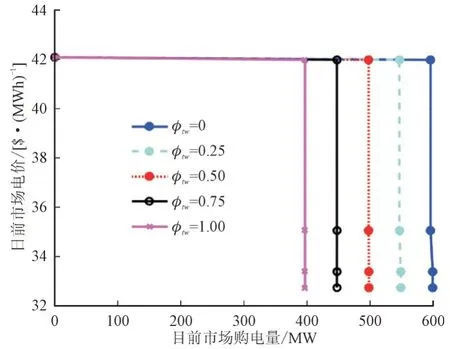
图9 13：00时电力零售商供给曲线图Fig.9 Retailer’s offering curves at 13:00

图9 的曲线说明，当电力零售商更倾向于购买更多的DRE 电力能源时，其在日前市场的报价会更低。

为了分析风险厌恶对电力零售商决策和期望成本的影响，将置信水平α设置为0.95，风险厌恶参数β取值范围为0～10。图10 展示了在不同φt,w值和β值的情况下，电力零售商总的预期采购成本和CVaR 值的关系曲线图。

图10 的曲线说明β值和φt,w值越大，电力零售商的总预期成本越高，并且对应的CVaR 值越低。电力零售商的预期成本增加是因为预期的DRE 价格高于日前市场和实时市场的价格。另一方面，电力零售商的CVaR 降低是因为DRE 价格的波动性低于日前市场和实时市场的价格。

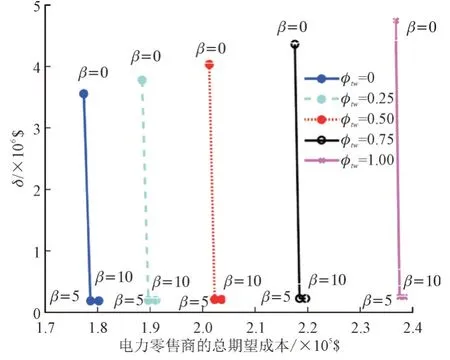
图10 不同β 值下电力零售商的总期望成本与CVaR值曲线图Fig.10 Total expected cost and CVaR of the retailer for different values of β

3 结语

本文提出了一个电力零售商参与自由化DRE市场的短期决策模型。当电力零售商市场代理的DRE 报价的预期值高于实时市场价格，且电力零售商设定了DRE 最小购电量时，日前和实时市场报价及DRE 报价会受到显著影响。针对这两种情况，本文所提出的模型都为电力零售商提供了不同风险厌恶水平下的最优决策。