The metric generalized inverse and its single-value selection in the pricing of contingent claims in an incomplete financial market

Zi WANG(王紫)

School of Mathematics Sciences，Harbin Normal University，Harbin 150025,China E-mail: zi_uwang@aliyun.com

Xiaoling WANG(王筱凌)t

Institute of Finance,Heilongjiang University of Finance and Economics，Harbin 150025,China.International School，Krirk Universitg，Bangkok 10220，Thailand E-mail: wangiaoling1985@alixun.com

Yuwen WANG(王玉文)

School of Mathematics Science,Harbin Normal University，Harbin 150025,China E-mail : wangyuwen1950@aliun.com

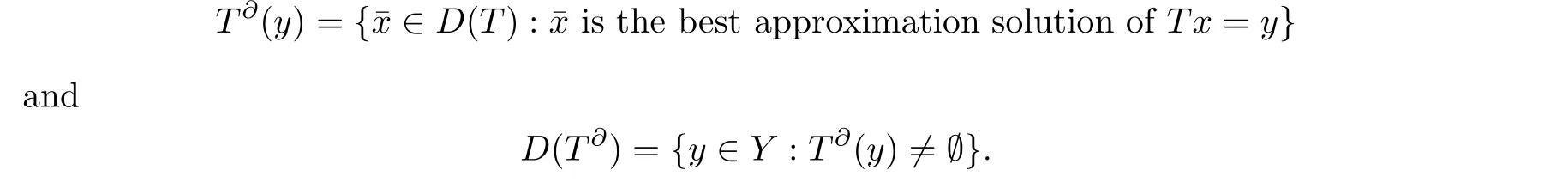
Set-valued mapping T∂: D(T∂) →2D(T)is called the (set-valued) metric generalized inverse[1] of T， where 2D(T)represents all the subsets of D(T).

A (generally nonlinear)single-valued operator Tσ:D(T∂)→X， satisfying Tσ(y)∈T∂(y)，is called the (single-valued) selection of (set-valued) metric generalized inverses.

In 1974， M.Z. Nashed and G.F. Votruba put forward research suggestions [1， 2] which showed that the problem of obtaining selections with nice properties for the metric generalized inverse merits study. Erdelyi and Ben-Israel[3]discussed the(single-valued)metric generalized inverse T∂for any linear operator T in a Hilbert space;in this case，denote it as T+. Y.M. Wei[4， 5] and J. Ding [4] studied the expression and perturbation analysis of the Moore-Penrose inverse and the weighted Moore-Penrose inverse in Hilbert space in 2001 and 2003，respectively.In 2003，H.Wang and Y.W.Wang[6]used the generalized Orthogonal Decomposition Theorem in Banach space to systematically study the general definition of the Moore-Penrose metric generalized inverse in Banach space and gave the basis of its existence and continuity. As a result， the foundation of the Moore-Penrose metric generalized inverse was laid [7]. Regarding the research suggestions proposed by M.Z. Nashed and G.F. Votruba [1]， it was not until 2008 that H. Hudzik， Y.W. Wang and W.J. Zheng [8] gave the condition of homogeneous (singlevalued) selection for the (set-valued) metric generalized inverse of the closed operator T in Banach spaces. In 2012， H.F. Ma， H. Hudzik and Y.W. Wang [9] gave the condition that the(set-valued) metric generalized inverse of the bounded linear operator T in a Banach space has continuous homogeneous selection. This paper continues the study of the research suggestions in[1]，and combines this with the pricing problem of incomplete financial markets，constructing a specific bounded linear operator A:ln1→l2from a non-reflexive Banach space ln1to a Hilbert space l2. The pricing problem is reduced to the (single-valued) selection Aσof (set-valued)metric generalized inverse A∂of A， and a selection with good properties (bounded linear) is obtained.

2 The Metric Generalized Inverse and its (Single-Value) Selection Model in an Incomplete Financial Market

In a financial market， it is generally assumed that the “contingent claims space” at time T in the future is the m=m(T)-dimensional vector space Rm. In view of the general assumption that the variance is limited， we let the l2norm ‖·‖2be given to Rm， where m is a positive integer related to T but is not fixed. In order to adapt to all considerations， we should choose

If θ takes over the vector in Rn(t)， then Aθ takes over the vector in Rm(T). We say that the financial market in a single time period [t，T] is complete. At this time， the price of each contingent claim in Rm(T)can be set by the price of the basic security through the linear pricing rule (equivalent to no arbitrage in the financial market) [10]. However， when the contingent claims do not belong to the range R(A) of the Pay-offmatrix A (when the financial market is incomplete， such contingent claims must exist)， or when the number of rows in the matrix is m(T) ＞n(t)， or the number of columns of the matrix is m(T) = n(t)， but the rank is r(A) ＜m(T)=n(t) of A， then the matrix A does not exists as the inverse matrix A-1， so we need to discuss the generalized inverse of A.

We must now ask: what kind of matrix generalized inverse is needed? This depends on the needs of the problem.

When the contingent claims space is selected as l2， for any positive integer n = n(t)， the financial market must be incomplete in the time period [t，T] (see [10]).

3 Main Result

4 Conclusion

For the contingent claim y ∈l2， since the financial market is incomplete， y may not be reachable，so it is impossible to price using a risk-neutral pricing method[10]. From the Hilbert property of the“contingent claims”space l2，the orthogonal projection PR(A)(y)∈R(A)satisfies

then it is the smallest according to the l1norm; that is， the absolute value of the proportion of shares invested in each risk asset is the smallest. Due to the non-strict convexity of the l1norm，the above set of x is a non-single point set. Direct pricing by all，satisfying(4.1)and the smallest x norm of l1， will violate the “law of one price”. However， ¯x=A+y is the only x that satisfies (4.1)， which is the smallest according to the l1norm and the smallest according to the l2norm point. Using ¯x = A+y to price PR(A)(y) not only satisfies the “law of one price”， but the weight of ¯x has reached the norm of l1and satisfied that the norm of l2is the smallest. The smallest norm of l2indicates that the “variance”of ¯x is the smallest， and the smallest norm of l1indicates that n risk assets are paired with the components of ¯x. The sum of the proportions of each share is the smallest.