Some equivalent conditions of proximinality in nonreflexive Banach spaces
2022-08-25ZihouZHANG张子厚YuZHOU周宇ChunyanLIU刘春燕JingZHOU周晶
Zihou ZHANG(张子厚) YuZHOU(周宇)Chunyan LIU(刘春燕)+Jing ZHOU(周晶)
School of Mathematics Phgsics and Statistics,Shanghai University of Engineering Science,Shanghai 201620,China E-mail: zhz@sues.edu.cn; roczhou-.fly@126.com; cyl@sues.edu.cn; zhoujing@sues.edu.cn


Obviously, the 1-Chebyshev set and the Chebyshev set are coincident; and the approximatively τ-compact 1-Chebyshev set and the τ-strongly Chebyshev set are coincident.
Remark 1.2 By [1, 7, 17], we know the following relations amongst the above proximinalities of a subset of X:
(1)τ-Strongly Chebyshev ⇒Approximatively τ-compact k-Chebyshev ⇒Approximatively τ-compact ⇒τ-Strongly proximinal ⇒Proximinal;
(2)τ-Strongly Chebyshev ⇒Chebyshev ⇒k-Chebyshev ⇒Compact Chebyshev ⇒Weakly compact Chebyshev ⇒Proximinal.
None of the implications can be reversed.
For a Banach space X, let X*be its dual space. For x ∈X, r >0, let S(x,r) = {y ∈X :‖y-x‖ = r}, B(x,r) = {y ∈X : ‖x-y‖ ≤r}. Let S(X) and B(X) be the unit sphere and the closed unit ball of X, respectively. Suppose that NA(X) is the set of all norm-attaining functionals on X and let S0(X*) = NA(X)∩S(X*). Let f ∈S(X*), JX(f) = {x ∈S(X) :f(x)=1}. Let x ∈S(X), JX*(x)={f ∈S(X*):f(x)=1}. Let {xi}ni=1⊂S(X),

(5) [3] nearly strictly convex (resp. weakly nearly strictly convex), if JX(f) is compact(resp. weakly compact) for any f ∈S(X*).
Remark 1.4 (1) By [13], we know that X is k-strongly convex if and only if X is nearly strongly convex and k-strictly convex; 1-strong convexity and strong convexity are equivalent.

(3) Sullivan [12] defined locally k-uniform rotundity (LKUR). Bandyopadhyay et al. [2]proposed almost locally uniform rotundity(ALUR)and weakly almost locally uniform rotundity(WALUR). It can be observed that LKUR, ALUR and WALUR are all generalizations of the classic locally uniform rotundity (LUR). From [13], we know that
LKUR ⇒k-strong convexity; Strong convexity ⇔ALUR; Very convex ⇔WALUR.
Proximinality is the core element of Approximation Theory, which characterizes the existence of the best approximation element. Because of the importance of proximinality in Approximation Theory, it is critical to clarify the relations between the type of proximinality.In this paper, we mainly study the following problem:
Problem 1.5 What are the conditions (necessary and sufficient or even just sufficient)that make the proximinality of a convex subset in Definition 1.1 equivalent?
In 2001, Fang and Wang [6] proved the following result:
Theorem 1.6 A Banach space X is nearly strongly convex (resp. nearly very convex) if and only if every proximinal convex subset of X is approximatively n-compact (resp. approximatively w-compact).
Theorem 1.6 is an interesting result, for it shows that nearly strong convexity(resp. nearly very convex) is the most appropriate structure for characterizing the equivalence of the relationship between the proximinality and the approximative n-compactness (approximative w-compactness) of convex subsets. Afterwards, Bandyopadhyay et al. [1], Guirao and Montersinos [10] and Zhang et al. [18] continued to explore this problem. Building offtheir results,we can obtain the following conclusions:
Theorem 1.7 Let X be a Banach space. Then the following statements are equivalent:
(1) X is nearly strongly convex (resp. nearly very convex);
(2) Every proximinal subspace of X is approximatively n-compact (approximatively wcompact);
(3) Every proximinal hyperplane of X is approximatively n-compact (approximatively wcompact);
(4) Every proximinal half-space of X is approximatively n-compact (approximatively wcompact).
Proof For the proof of (2) ⇔(3), see [1]. For the proof of (1) ⇔(3), see [10]. For the proof of (1)⇔(4), see [18]. □
The convexity of the subset in X is the key to proving Theorems 1.6 and 1.7. If the convex subset is changed to a general subset in the condition, are Theorem 1.6 and Theorem 1.7 still true? Motivated by this question, we naturally come to the following problem:
Problem 1.8 For the general subset of a Banach space, what are the necessary and sufficient conditions that make proximinal and approximatively τ-compact sets equivalent?
In this paper, we mainly focus on solving Problems 1.5 and 1.8. We obtain some equivalent conditions regarding the proximinality. In addition, we give characterizations which establish that a half-space is τ-strongly proximinal, τ-strongly Chebyshev, and approximatively τ-compact.
2 Main Result s


(2) Every proximinal convex subset of X is approximatively n-compact (resp. approximatively w-compact) k-Chebyshev;
(3) Every proximinal subspace of X is approximatively n-compact (resp. approximatively w-compact) k-Chebyshev;
(4) Every proximinal half-space of X is approximatively n-compact(resp. approximatively w-compact) k-Chebyshev;
(5)Every proximinal hyperplane of X is approximatively n-compact(resp. approximatively w-compact) k-Chebyshev.
Remark 2.5 By[13,Theorem 3.3],we know that k-strong convexity(resp. k-very convex)implies that we have (k +1)-strong convexity (resp. (k +1)-very convex), but the contrary is not true. Therefore, an approximatively n-compact (resp. approximatively w-compact)k-Chebyshev set implies an approximatively n-compact (resp. approximatively w-compact)(k+1)-Chebyshev set, but the contrary is not true.
By Theorem 2.4, we immediately get
Corollary 2.6 Let X be a Banach space. Then the following statements are equivalent:
(1) X is strongly convex (resp. very convex);
(2)Every proximinal convex subset of X is n-strongly Chebyshev(resp. w-strongly Chebyshev);
(3)Every proximinal subspace of X is n-strongly Chebyshev(resp. w-strongly Chebyshev);
(4)Every proximinal half-space of X is n-strongly Chebyshev(resp. w-strongly Chebyshev);
(5) Every proximinal hyperplane of X is n-strongly Chebyshev (resp. w-strongly Chebyshev).
In [1], Bandyopadhyay et al. proved the following conclusion:
Lemma 2.7 Let C be τ-closed subset of a Banach space X and let x0∈XC. Then C is approximatively τ-compact for x0if and only if C is τ-strongly proximinal for x0and PC(x0)is τ-compact.
By Theorem 1.6, Theorem 1.7 and Lemma 2.7, we can directly get
Lemma 2.8 Let X be a Banach space. The following statements are equivalent:
(1) X is nearly strongly convex (resp. nearly very convex);
(2) Every proximinal convex subset of X is n-strongly proximinal and compact Chebyshev(resp. w-strongly proximinal and weakly compact Chebyshev);
(3)Every proximinal subspace of X is n-strongly proximinal and compact Chebyshev(resp.w-strongly proximinal and weakly compact Chebyshev);
(4) Every proximinal hyperplane of X is n-strongly proximinal and compact Chebyshev(resp. w-strongly proximinal and weakly compact Chebyshev);
(5) Every proximinal half-space of X is n-strongly proximinal and compact Chebyshev(resp. w-strongly proximinal and weakly compact Chebyshev).
Lemma 2.9 Let X be a Banach space, and let r >0. Then X is nearly strictly convex(resp. weakly nearly strictly convex) if and only if every convex subset of S(0,r) is relatively compact (resp. relatively weakly compact).
Proof Suppose that C is a convex subset of S(0,r). From the separation theorem, there exists a f ∈S(X*) such that
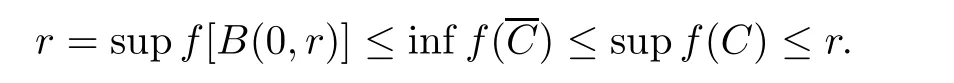

Conversely, since rJX(f) is a convex subset of S(0,r) for every f ∈S(X*), JX(f) is a compact set, by assumption. This means that X is nearly strictly convex. □
Lemma 2.10 Let X be a Banach space. Then the following statements are equivalent:
(1) X is nearly strictly convex (resp. weakly nearly strictly convex);
(2) Every proximinal convex subset of X is compact Chebyshev (resp. weakly compact Chebyshev);
(3) Every proximinal subspace of X is compact Chebyshev (resp. weakly compact Chebyshev);
(4)Every proximinal hyperplane of X is compact Chebyshev(resp. weakly compact Chebyshev);
(5)Every proximinal half-space of X is compact Chebyshev(resp. weakly compact Chebyshev).
Proof (1) ⇒(2). Let C be a proximinal convex subset of X. Then PC(x) /= Ø for all x ∈X. If C is not compact Chebyshev, then there exists a x ∈X such that PC(x) is not compact. Since PC(x) is convex, and for any y ∈PC(x), ‖x-y‖ = d(x,C) = d, we can get that the set S(x,d) contains a noncompact convex subset PC(x). However, by assumption, X is nearly strictly convex, and combined with S(x,d) = x+S(0,d), we know from Lemma 2.9 that every convex subset of S(x,d) is relatively compact. This is a contradiction. Hence C is compact Chebyshev.

Theorem 2.11 Let X be a Banach space. The following statements are equivalent:
(1) X is nearly strongly convex (resp. nearly very convex);
(2) Every proximinal convex subset of X is n-strongly proximinal and X is nearly strictly convex (resp. weakly nearly strictly convex);
(3)Every proximinal subspace of X is n-strongly proximinal and X is nearly strictly convex(resp. weakly nearly strictly convex);
(4) Every proximinal hyperplane of X is n-strongly proximinal and X is nearly strictly convex (resp. weakly nearly strictly convex);
(5) Every proximinal half-space of X is n-strongly proximinal and X is nearly strictly convex (resp. weakly nearly strictly convex).
Corollary 2.12 Let X be a Banach space. Then the following statements are equivalent:
(1) X is k-strongly convex (resp. k-very convex);
(2) Every proximinal convex subset of X is n-strongly proximinal k-Chebyshev (resp. wstrongly proximinal k-Chebyshev);
(3)Every proximinal subspace of X is n-strongly proximinal k-Chebyshev(resp. w-strongly proximinal k-Chebyshev);
(4) Every proximinal hyperplane of X is n-strongly proximinal k-Chebyshev (resp. wstrongly proximinal k-Chebyshev);
(5) Every proximinal half-space of X is n-strongly proximinal k-Chebyshev (resp. wstrongly proximinal k-Chebyshev).
Proof By Lemma 2.3 and Theorem 2.11, we have that (1) ⇒(2) ⇒(3) ⇒(4), (1) ⇒(2)⇒(5).
(4) ⇒(1). By Lemma 2.3, we have that X is k-strictly convex. Since k-strict convexity implies nearly strict convexity, we know, by Theorem 2.11, that X is nearly strongly convex.Hence, X is k-strongly convex, by Remark 1.4(1).
(5)⇒(1). The proof is similar to (4)⇒(1). □
Remark 2.13 According to the above results,we can get some sufficient conditions that establish the proximinality of a convex subset of X.



杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- THE GENERALIZED HYPERSTABILITY OF GENERAL LINEAR EQUATION IN QUASI-2-BANACH SPACE*
- NO-ARBITRAGE SYMMETRIES*
- O(t-β )-synchronization and asymptotic synchronization of delayed fractional order neural networks
- On the dimension of the divergence set of the Ostrovsky equation
- MAXIMAL L1-REGULARITY OF GENERATORS FOR BOUNDED ANALYTIC SEMIGROUPS IN BANACH SPACES*
- Weighted norm inequalities for commutators of the Kato square root of second order elliptic operators on Rn
