THE GENERALIZED HYPERSTABILITY OF GENERAL LINEAR EQUATION IN QUASI-2-BANACH SPACE*
2022-08-25RavinderKumarSHARMASumitCHANDOK
Ravinder Kumar SHARMA Sumit CHANDOK
School of Mathematics, Thapar Institute of Engineering and Technology, Patiala-147004, India E-mail: ravindersharma880@gmail.com; sumit.chandok@thapar.edu
Abstract In this paper, we study the hyperstability for the general linear equation
Key words Hyperstability; quasi-2-Banach spaces; fixed point; general linear equation
1 Introduction and Preliminaries
The main motivation for the investigation of the stability of functional equations was given by Ulam in 1940 in his talk at the university of Wisconsin [27]. Hyers [17] gave affirmative partial answer to the question of Ulam in Banach space. After that Aoki[3] generalized Hyers’Theorem for additive mapping and Rassias [26] generalized Hyers theorem for linear mapping by considering an unbounded Cauchy difference. In 1994, G˘avruta [14] generalized Rassias’theorem and discuss the stability of linear functional equation.
During the last four decades,many results concering the Hyers-Ulam stability of important functional equations have been obtained by several mathematicians (see [1, 19, 22, 28–30] and references cited therein).
A functional equation is hyperstable if a function satisfying the equation approximately is a true solution of it. In 1949, Bourgin [5] gave the first hyperstability result and concerned the ring homomorphisms. The hyperstability results of the several functional equation in the literature have been studied by many authors in recent years(see[4,6,7, 10–12, 15,20, 23,24]and references cited therein).

In this paper, we extend Theorem 1.1 in the setting of quasi 2-Banach space. Also, we obtian some results for the hyperstability of the general linear equation (1.1) in the setting of quasi-2-Banach spaces.
2 Properties of Quasi-2-Normed Space
In this section, we present some definitions and properties of quasi-2-normed space which will be used in the sequel.
In 1965, G¨ahler [16] introduced 2-normed spaces. One of the axioms of the 2-norm is the parallelepiped inequality, which is a fundamental in the theory of 2-normed spaces. Park [21]replaced precisely this inequality(analogously as in the normed spaces)with a new more general condition, and gave the concept of quasi-2-normed spaces and quasi-(2;p)-normed spaces.
Definition 2.1 Let X be a real linear space of dimension greater than 1 and ‖·,·‖ be a real valued function on X×X satisfying the following four conditions:
(N1) ‖x,y‖ = 0 if and only if x and y are linearly dependent in X;
(N2) ‖x,y‖ = ‖y,x‖ for all x,y ∈X;
(N3) ‖x,αy‖ = |α|.‖x,y‖ for every real number α;(N4) ‖x,y+z‖≤‖x,y‖+‖x,z‖ for all x,y,z ∈X.
Then function ‖·,·‖ is called 2-norm on X and the pair (X,‖·,·‖) is a called 2-normed space.
Definition 2.2 Let X be a linear space. A quasi-2-norm is a real-valued function on X ×X satisfying (N1),(N2),(N3) of Definition 2.1 and
(N5) ‖x+y,z‖≤K‖x,z‖+K‖y,z‖,for all x,y,z ∈X and K ≥1.
If ‖·,·‖ is a quasi-2-norm on X, then (X,‖·,·‖,K) is called quasi-2-normed space. The smallest possible K is called the modulus of concavity of ‖·,·‖.
A quasi-2-norm ‖·,·‖ is called quasi-p-norm (0 <p <1) if ‖x+y,z‖p≤‖x,z‖p+‖y,z‖p,for all x,y,z ∈X.
Every 2-normed space is a special case of quasi-2-normed spaces (for K =1).
Example 2.3 Assume that X = R3and x = x1i+x2j+x3k, y = y1i+y2j+y3k ∈R3.Define


Proposition 2.6 Every quasi-2-Cauchy sequence in a quasi-2-normed space is quasi-2-bounded.
Proof Suppose that {xn} is a quasi-2-Cauchy sequence in a quasi-2-normed space X.Thus by the definition, for all ε=1 >0, there exists N ∈N such that

Now, we have to show that {xn} is quasi-2-bounded; that is ‖xn,z‖ <M. Using triangle inequality, we have

and this is true for all n >N. By choosing the maximum of either 1 + ‖xN+1,z‖ or the maximum of the aforementioned set, we can find our M which bounds all the terms in the sequence. Hence, the result is obtained. □
Definition 2.7 Let X be a real linear space of dimension greater than 1. Quasi-2-norms|||·,·||| and ||·,·|| define on X are equivalent if it exists m,M >0 such that

Lemma 2.8 Let (X,‖·,· ‖) be quasi-2-normed space. There is a p(0 <p ≤1) and equivalent quasi-2-norm |||·,·||| on X satisfying |||x + y,z|||p≤|||x,z|||p+ |||y,z|||p, for all x,y,z ∈X.
Here, it is to note that quasi-2-norm is not continuous but its equivalent norm defined by(2.1) is continuous.

3 Fixed Point
The basic tool in this paper is the following theorem which assert the existence of a unique fixed point of the function T : YX→YX. This result is the extension of Theorem 1.1 from 2-Banach space to quasi-2-Banach space using Lemmas 2.8 and 2.9.


By combining (3.9) and (3.3), the sequence {(Tnφ)(x)} is a quasi-2-Cauchy sequence in the equivalent quasi-2-normed (Y, |||·,·|||). Using (2.2), {(Tnφ)(x)} is also quasi-2-Cauchy in(Y,‖·,·‖,K). Since Y is complete, there exists the following limit in (Y,‖·,·‖,K):



4 Hyperstability of Functional Equation
In this section, we obtain the hyperstability of functional equation (1.1) in the setting of quasi-2-Banach spaces using Theorem 3.1.
Theorem 4.1 (1)Let(X,‖·,·‖,K)be a quasi-2-normed space over the field F,(Y,‖·,·‖,K)be a quasi-2-Banach space over the field K and Z0be a subset of Y containing two linearly independent vectors.
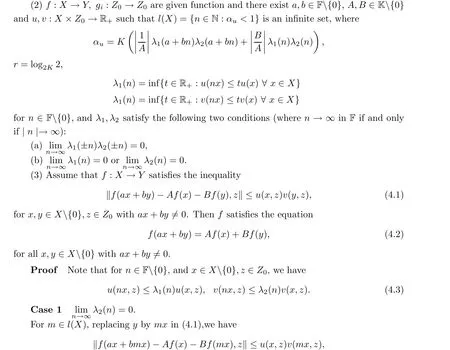





for all x,y ∈X{0} with ax+by /=0.

杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- NO-ARBITRAGE SYMMETRIES*
- O(t-β )-synchronization and asymptotic synchronization of delayed fractional order neural networks
- On the dimension of the divergence set of the Ostrovsky equation
- MAXIMAL L1-REGULARITY OF GENERATORS FOR BOUNDED ANALYTIC SEMIGROUPS IN BANACH SPACES*
- Weighted norm inequalities for commutators of the Kato square root of second order elliptic operators on Rn
- The discrete Orlicz-Minkowski problem for p-capacity
