Transonic shock solutions to the Euler system in divergent-convergent nozzles

Ben DUAN(段森)

School of Mathematical Sciences，Jilin University，Changchun 130012,China E-mail: bduan @jlu.edu.cn Ao LAN(兰傲)

School of Mathematics，Dalian University of Technology，Dalian 116024，China E-mail : alan18@mail.dlut.edu.cn

Zhen LUO(罗珍)+

School of Mathematical Sciences，Xiamen University，Xiamen 361005，China E-mail : zluo @rmu.edu.cn

In previous works，there have appeared numerous significant results about the Euler system for subsonic and supersonic flows;we refer interested readers to[3–8]and the references therein.Another important flow pattern is transonic flow. A flow is called transonic if it contains both subsonic and supersonic regions. Moreover， the subsonic and supersonic regions are connected by shocks and sonic curves， which， in general， are free interfaces. This leads to some essential difficulties for the mathematical analysis of transonic flows. In this paper， we aim to study the existence of steady discontinuous transonic flow patterns in a nozzle， that is， transonic shocks.

A steady transonic shock solution is a piecewise C1solution of (1.5) with two C1solutions separated by a shock connecting a supersonic state on the left to a subsonic state on the right.We give the strict definition of the transonic shock solution to (1.5)–(1.6) as follows:

Definition 1.1 A transonic shock solution located at x*∈(-L，L)to the boundary value problem (1.5)–(1.6) can be formulated as

We would like to investigate the existence of transonic shock solutions to system(1.5)–(1.6)in a quasi-one-dimensional divergent-convergent nozzle (see Figure 1). Suppose that the cross section of the nozzle A(x)＞0 is a C1function and satisfies the conditions

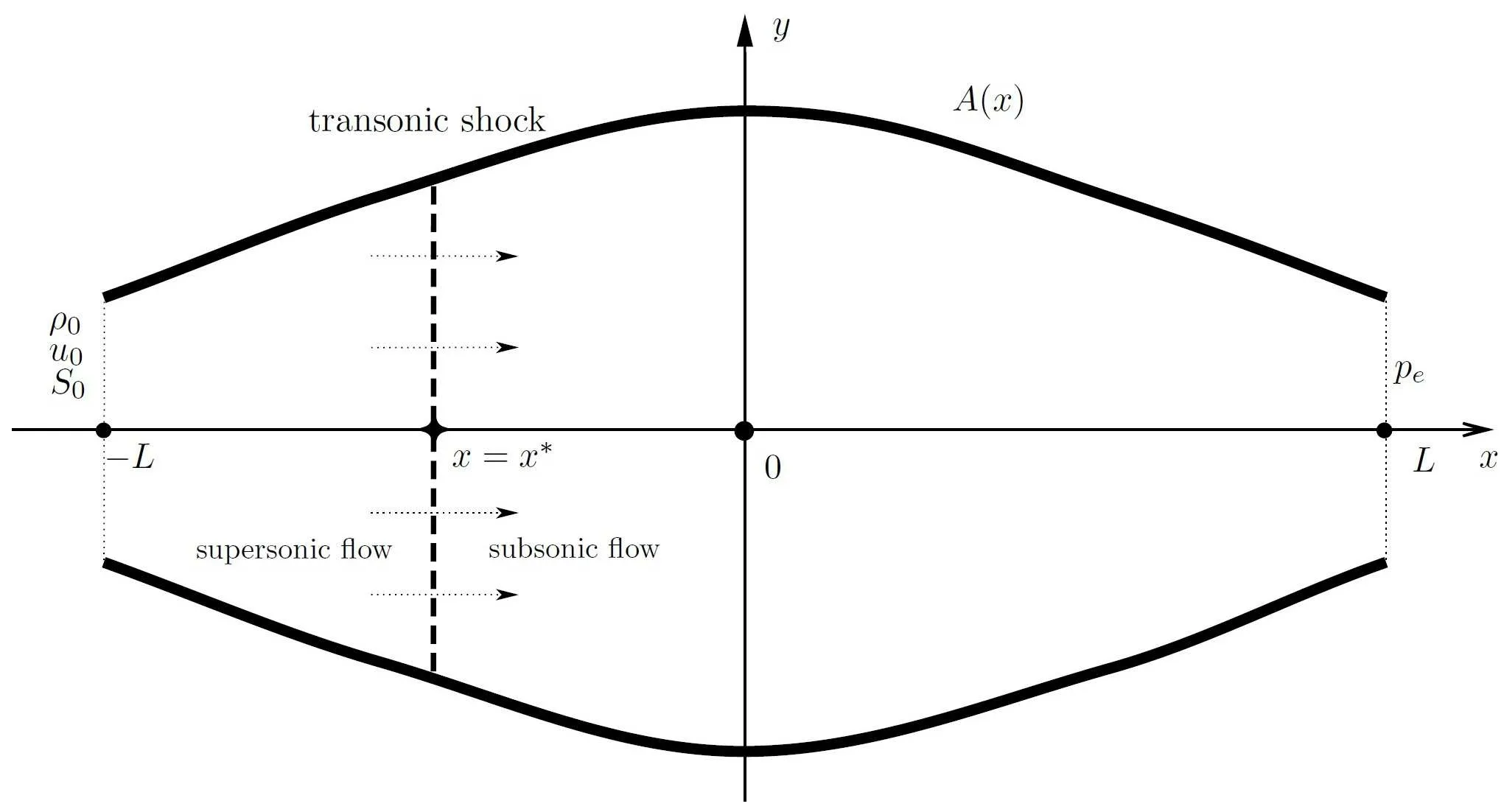
Figure 1 Divergent-convergent nozzle

It follows from the first equation in (1.5) and (1.12) that

In [9]， Courant and Friedrichs described the transonic shock phenomena in a de Laval nozzle，stating that if the receiver pressure lies in a certain interval，subsonic inflow will become sonic at the throat of the nozzle， and will then accelerate to supersonic at a divergent nozzle.Finally， the flow will become subsonic after a shock front. However，there have not been many theoretical analyses of this transonic shock phenomena. According to the above phenomena，Chen [10] and Li， Xin and Yin [11] showed the well-posedness of the transonic shock problem with a prescribed flow on the entrance and suitable pressure on the exit of a divergent nozzle.In two dimensional and three dimensional nozzles，the existence and stability of transonic shock solutions were obtained by giving some additional restrictions; please refer to [12， 13]. Later on， for a multidimensional divergent nozzle with an arbitrary smooth cross-section， Bae and Feldman [14] obtained non-isentropic potential transonic shocks with a given exit pressure.Based on the theory in [15]， Xie and Wang [16] constructed a single transonic shock wave pattern in an infinite nozzle which asymptotically converges to a cylinder. They also obtained the stability of the uniform transonic wave. Chen [17] proved the stability of the planar steady shock in a straight two dimensional tube. Recently， Chen and Fang studied the stability of multidimensional transonic shock solutions in a steady supersonic flow in [18]. For the quasione-dimensional system， there have been many important results obtained by Liu [2， 19] and by Rauch， Xie and Xin [20]. Some other important progress on the existence and stability of transonic shocks in a nozzle were achieved in[21–24]. There also exists smooth transonic flows;please see [25， 26] and the references therein.

However， in all of these fruitful and significant results on nozzle flow problems， there is at most one transonic shock solution with a physical boundary condition. In [27]， Luo and Xin investigated the steady isentropic Euler-Poisson system， and obtained the non-uniqueness of transonic shock solutions for a class of boundary conditions. Motivated by their creative work，we study the existence of exactly two transonic shock solutions to the non-isentropic Euler system in quasi-one-dimensional divergent-convergent nozzles. For the given supersonic inflow and appropriately large receiver pressure pe， if the receiver pressure pelies in a certain interval，then it can be proved that there exist exactly two transonic shock solutions (see Theorem 1.2).Furthermore， the location of the transonic shock is monotonic with respect to the pressure downstream (see Lemma 3.1).

Our existence theorem of transonic shock solutions is the following:

Theorem 1.2 For the given positive constants L， J and γ ＞1， there exists a non-empty parameter set B such that if (ρ0，u0，S0) ∈B， then there exists an interval I = (p，p)， and the boundary value problem(1.5)–(1.6)，(1.10)–(1.12)admits exactly two transonic shock solutions on [-L，L] for downstream pressure pe∈I.

Remark 1.3 Following the framework of Liu in [2， 19]， the dynamical stability of the two transonic shock solutions obtained in Theorem 1.2 can also be analyzed. It seems that the transonic shock solution is dynamically stable if the shock location is at the divergent part，and the other transonic shock solution with shock location at the convergent part is dynamically unstable. It would be interesting to study the dynamical stability of these two solutions， but this is left for the future.

The rest of this paper is organized as follows: in Section 2， the existence of C1transonic shock solutions to the boundary value problem (1.5)–(1.6) on [-L，L] is obtained. Section 3 is devoted to proving the monotonicity between the location of the transonic shock and the exit pressure; this yields the existence of exactly two transonic shock solutions.

2 Solvability of Transonic Shock Solutions

In this section， we construct transonic shock solutions to problem (1.5)–(1.6) on [-L，L]when the entrance data lies in a suitable non-empty set.

3 Proof of the Main Theorem

In this section， the monotonicity between the location of the transonic shock and the exit pressure is obtained. Moreover， the existence of exactly two transonic shock solutions is established.

Lemma 3.1 Let L，J ＞0， γ ＞1 be given constants. For any upstream boundary data(ρ0，u0，S0) ∈B and any x*∈(-L，L)， let (ρ，u，S)(x) be the transonic shock solution located at x*to the boundary value problem (1.5)–(1.6) on [-L，L]. Assume that p+(L;x*) is the

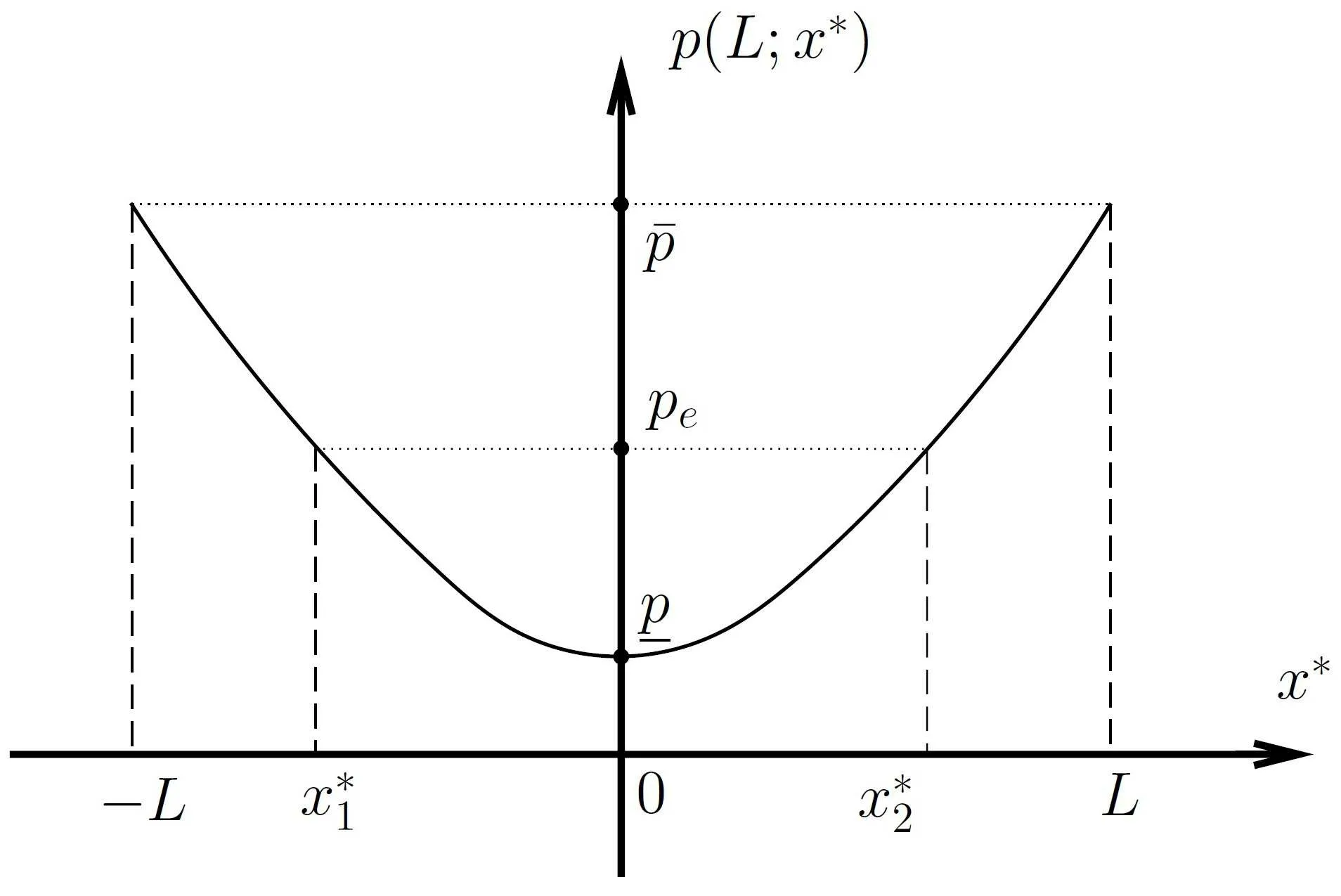
Figure 2

Indeed， (ρ-，u-，S-)(x*) is solved by the supersonic solution with the initial value (ρ0，u0，S0) ∈B， while (ρ+，u+，S+)(x*) is obtained by (2.13). (ρe，ue，Se) is obtained by the subsonic solution with the initial value (ρ+，u+，S+)(x*). Furthermore， by Lemma 2.2， the entropy condition holds.

This completes the proof of Theorem 1.2.