The stability of the delta wave to pressureless Euler equations with viscous and flux perturbations
2022-08-25SijieLIU刘思杰WanchengSHENG盛万成
Sijie LIU(刘思杰)Wancheng SHENG(盛万成)1
Department of Mathematics,Shanghai University,Shanghai 200444,China E-mail : lsj999@shu.edau.cn; mathwwcsheng@shu.edau.cn



Physically, viscous perturbation can be seen as a regularization originating from fluid mechanics, and flux perturbation can be used to govern some dynamical behaviors of fluids. Thus it is quite meaningful to study the existence of Riemann solutions to (1.11) and the limit of Riemann solutions as ε,κ →0.
There are two respects in which our result goes beyond [7]. One is that there are two perturbations in system (1.3): viscous and flux. The limit of solutions to (1.11) regards to parameters ε,κ. The second respect is that we conclude that the Riemann solutions to (1.11)cannot be uniformly bounded with respect to ε,κ, thus the weak limit of Riemann solutions to(1.11) can only be the delta wave.
This paper is organized as follows: in Section 2, we recall the solutions of (1.3) and (1.12).In Section 3, we present the existence of classical solutions of (1.13) and (1.14). In Section 4, we consider whether the solutions of (1.13) and (1.14) are uniformly bounded with respect to parameters ε,κ when u->u+. In Section 5, we prove that Riemann solutions of (1.11)converge to a delta wave in the sense of distribution in the case u->u+.
2 Riemann Solutions of Systems (1.3) and (1.12)
The system(1.3)has a double eigenvalue λ=u with the corresponding right eigenvector →r =(1,0)Tsatisfying ∇λ·→r =0,hence system(1.3)is non-strictly hyperbolic and the characteristic field is linearly degenerate.
Consider the self-similar solutions of the Riemann problem (1.3) and (1.12):


3 Existence of a Solution to the Regularized Problem (1.13)–(1.14)
In this section, we present the existence of classical solutions to the regularized systems(1.13)and(1.14). We mainly discuss the situation in which the delta wave appears. Henceforth,we assume that





4 ρε,κ(ξ) Cannot be Uniformly Bounded Regarding ε,κ


From Theorem 4.4, we get that the unique discontinuity of (ρ(ξ),u(ξ)) appears at ξ = θ.However,u->u+shows that u(θ-)/=u(θ+). Thus,the Rankine-Hugoniot condition does not hold, which implies a contradiction. Thus, for any subsequence {ρεn,κn(·),uεn,κn(·)} cannot be uniformly bounded, where εn,κn→0 as n →∞.
By Theorem 4.1, Theorem 4.2, and Theorem 4.3, we obtain that only the following occur:
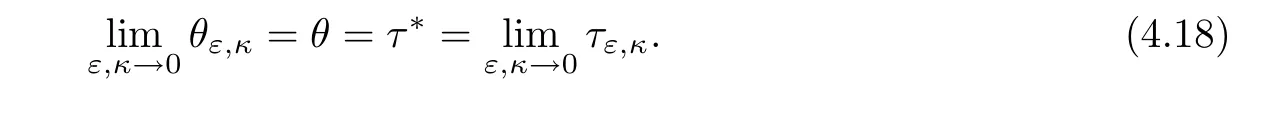
5 The limit of Solutions to (1.11)–(1.12) as ε,κ →0




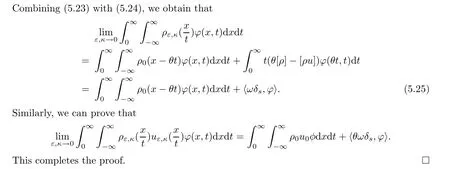
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- THE GENERALIZED HYPERSTABILITY OF GENERAL LINEAR EQUATION IN QUASI-2-BANACH SPACE*
- NO-ARBITRAGE SYMMETRIES*
- O(t-β )-synchronization and asymptotic synchronization of delayed fractional order neural networks
- On the dimension of the divergence set of the Ostrovsky equation
- MAXIMAL L1-REGULARITY OF GENERATORS FOR BOUNDED ANALYTIC SEMIGROUPS IN BANACH SPACES*
- Weighted norm inequalities for commutators of the Kato square root of second order elliptic operators on Rn
