A new proof of Gaffney’s inequality for differential forms on manifolds-with-boundary:the variational approach á la Kozono-Yanagisawa

Siran LI (李思然)

School of Mathematical Sciences,IMA-Shanghai & Key Laboratory of Scientific and EngineeringComputing (Ministry of Education)，Shanghai Jiao Tong University，Shanghai 200240,China E-mail : siran.li @sjtu.edu.cn

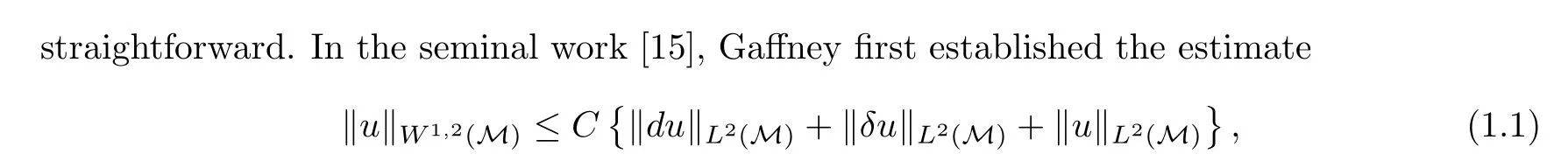
where M has an empty boundary and u is a differential k-form on M for any k;see also Gallot–Meyer [16] and the exposition in Schwarz [29] (especially Corollary 2.1.6 and Theorem 2.1.7).

The proof of Equation(1.1)for general r ∈]1，∞[(i.e.， with W1，2and L2replaced by W1，rand Lr， respectively) in boundary value spaces is more technical. Iwaniec–Scott–Stroffolini[21] utilised the “freezing coefficient” argument to prove the Lr-Gaffney inequality via essentially local and Euclidean computations. Global proofs of Equation(1.1)on manifolds without boundary can be found in the literature; cf. Scott [30] for a potential-theoretic proof via the Lr→Lrboundedness of Riesz transforms. Extensions to various classes of open manifolds are also available (Amar [1]， Auscher–Coulhon–Duong–Hofmann[3]， etc.).

In contrast， in the Hilbert case (r = 2)， global， geometric， and simple proofs of Gaffney’s inequality on Riemannian manifolds-with-boundary and Euclidean domains can be found in the literature. Wider classes of boundary conditions and the determination of best constants have also been investigated; see Georgescu [17]， Cast´o [6]， Cast´o–Dacorogna [7]， Cast´o–Dacorogna–Kneuss [8]， Cast´o–Dacorogna–Sil[9]， Cast´o–Dacorogna–Rajendran[10]， and Mitrea [25].

Brought to our attention have been two global proofs for the Lr-Gaffney inequality for general r ∈]1，∞[ in Dirichlet/Neumann boundary value spaces. Using a Campanato method，Sil [31] established the boundary regularity for more general classes of elliptic systems of differential forms in boundary value spaces. Also， Kozono–Yanagisawa [24] proved a generalised Lax–Milgram theorem and used it to deduce the Lr-Hodge decompositions for differential forms with Dirichlet/Neumann boundary values. The Lr-Gaffney inequality was obtained along the way in [24， 31].

In this note， we present an alternative proof of the Lr-Gaffney inequality for differential forms of arbitrary order on manifolds-with-boundary. As opposed to the above two approaches，i.e.， the functional-analytic arguments by Kozono–Yanagisawa [24] and the Campanato space estimates by Sil [31]， we demonstrate the Lr-Gaffney inequality – which，in greater generality，shall be formulated on Riemannian manifolds-with-boundary–via global geometric arguments.

More precisely，our approach to the Lr-Gaffney inequality is based on the Bochner technique and integration by parts (i.e.， the Stokes and/or Gauss–Green theorems)， together with a variational characterisation of W1，r-differential forms in boundary value spaces `a la Kozono–Yanagisawa [24]. In addition， we make use of a polarisation trick to exploit the symmetry of boundary integrals. We learned this trick from an earlier work [5] by Chern.

1.2 Boundary value Sobolev spaces for differential forms on manifolds-with-boundary

Let us first introduce the relevant function spaces. Our notations largely follow those of Schwarz [29].

Throughout this work， (M，g0) is a Riemannian manifold-with-boundary of dimension n.Denote by Ωk(M)the space of differential k-forms on M. One can define in standard ways the Sobolev spaces of differential forms; see Hebey [18]. We write

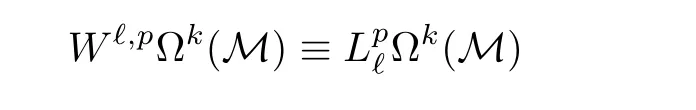
for the space of k-forms on M with Wℓ，p-regularity in the interior.

We write d:Ωk(M)→Ωk+1(M)for the exterior differential operator，and δ :Ωk+1(M)→Ωk(M) for the codifferential (i.e.， the formal L2-adjoint of d). Throughout， the L2- and any other Sobolev norms on M are all taken with respect to the underlying Riemannian metric g0.The Hodge star ⋆:Ωk(M)→Ωn-k(M) is also defined via the Riemannian volume measure.

On the space ˚W1，rΩk(M) :=｛u ∈LrΩk(M): du ∈LrΩk+1(M)， δu ∈LrΩk-1(M)｝， we can define the Dirichlet and Neumann trace operators t and n as follows:

is the Riemannian volume (surface) form on ∂M.

For background materials on global/geometric analysis， we refer to Petersen [28]， Hebey[18]， and the first chapter of Schwarz [29].

1.3 Main Theorem

1.4 Variational approach

The case for n = 3， g0= the Euclidean metric， and k = 1 is due to Kozono–Yanagisawa[23]，and based on this a new，refined proof of the Hodge decomposition theorem for vectorfields is obtained. We shall essentially follow the strategies in [23] to prove Theorem B.

1.5 Organization

The remaining parts of this note are organised as follows: first， in Section 2 we collect a few preliminary results on geometry. Next， in Section 3， a proof of Theorem B shall be given by generalising the arguments in [23] for vectorfields on 3D domains. This shall be utilised in Section 4 to prove Theorem A. Indeed， our arguments in Section 4 are global. Finally， several concluding remarks will be given in Section 5.

2 Preliminaries

Let us first note the following commutation relations between the differential， the codifferential， the Hodge star， and the trace operators:

Lemma 2.1 For any sufficiently regular differential k-form ω and (k+1)-form η on the manifold-with-boundary (Mn，g0)， we have

3 Variational Inequalities

3.1 The case of Rn

In this subsection (·，·) always denotes the standard Euclidean inner product. We shall prove

3.2 The case of

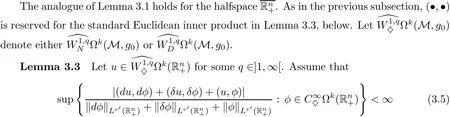
3.3 The case of a small chart

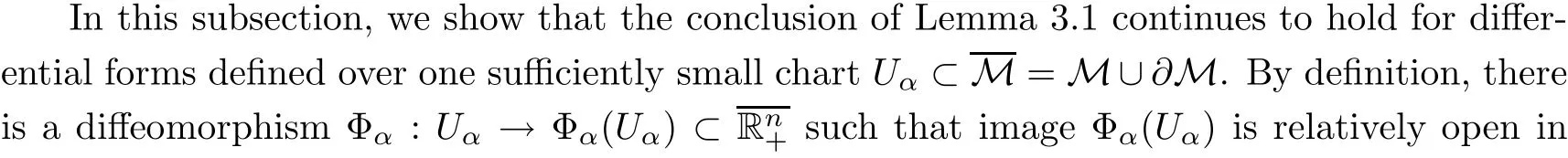
3.4 Proof of Theorem B

Finally， we are in position to conclude the proof of Theorem B. The cases ◇= D and N shall the treated simultaneously.

Since M is bounded， when q ≥r there is nothing to prove (as LqΩk(M) ⊂LrΩk(M)).Thus we assume throughout， in the sequel， that

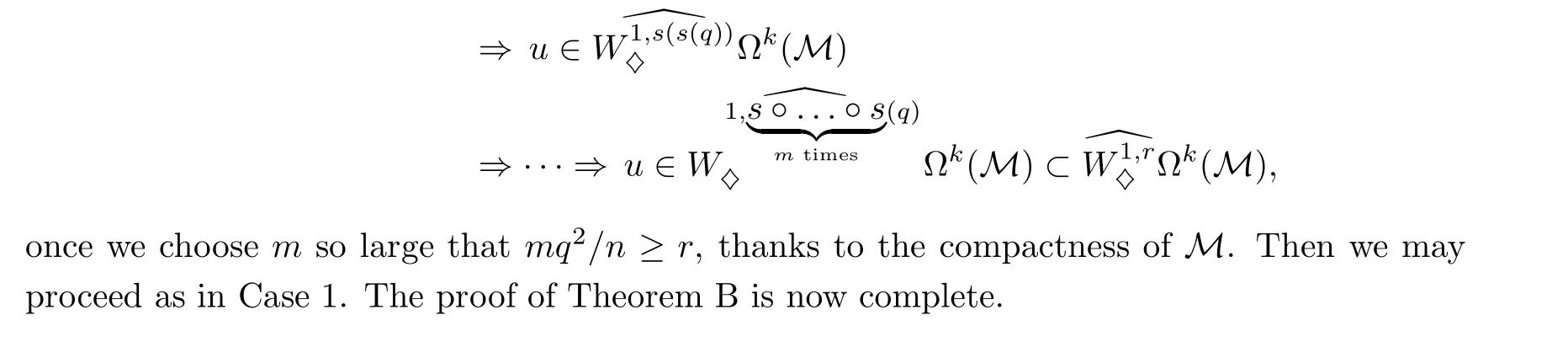
3.5 A Remark

4 Proof of Gaffney’s Inequality

As φ is purely perpendicular at the boundary，∇βφ is too for any tangential index β /=ν. Thus，the first term on the right-hand side of the final equality vanishes constantly on ∂M. The other two terms contain no derivatives of φ， therefore the covariant derivatives fall on eγ(for tangential γ)， and hence can be expressed in terms of the Christoffel symbols.

Putting the above arguments together， we deduce from D(u，φ) = I + J the following expression:

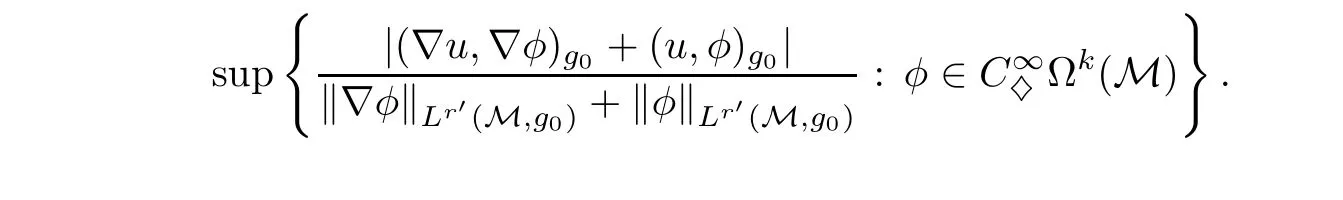
5 Concluding Remarks

Gaffney’s inequality is the key estimate for the Hodge decomposition theorem for differential forms in boundary value Sobolev spaces. With Theorem A established， we can easily deduce the Hodge decomposition from standard functional analysis;see the exposition by Schwarz[29]and Iwaniec–Scott–Stroffolini [21]， as well as the classical papers of Helmholtz [19]， Weyl [34]，Hodge [20]， Kodaira [22]， Duff–Spencer [12]， Friedrichs [14]， Morrey [26， 27]， and the recent contributions by Dodziuk [11]， Borchers–Sohr[4]， Simader–Sohr [32]， Wahl [33]， etc.

One should remark that all the results in this paper remain valid for manifolds-withboundary (M，g0) with C1-bounded geometry.

Our arguments in Section 4 circumvent the local computations in Euclidean space via the so-called Bochner technique. Very roughly speaking， the Bochner technique seems to be more suitable for the L2-setting. In this note， nevertheless， we have successfully applied it in non-Hilbert settings. This is precisely due to the variational characterisation of the W1，r-norm of differential forms in Theorem B `a la Kozono–Yanagisawa[23].

Acknowledgements We are deeply indebted to Gyula Csat´o and Swarnendu Sil for kind communications and discussions on recent developments concerning Gaffney’s inequality.Gratitude is also extended to Pengfei Guan， from whom we learned about Chern’s work [5]and the polarisation trick therein. We also thank the referees for their careful reading of the manuscript and for their constructive suggestions， and for pointing out the references [17， 24].