The existence and blow-up of the radial solutions of a (k1, k2)-Hessian system involving a nonlinear operator and gradient
2022-08-25GuotaoWANG王国涛ZedongYANG杨泽栋
Guotao WANG(王国涛)Zedong YANG(杨泽栋)
School of Mathematics and Computer Science,Shanai Normal University,Taiyuan 030031,China E-mail: wgt2512@163.com; yangzd1229@163.com.
JiafaXU (徐家发)*
School of Mathematical Sciences,Chongqing Normal University,Chongqing 401331,China E-mail: rujiafa.292@sina.com
Lihong ZHANG(张丽红)
School of Mathematics and Computer Science,Shanai Normal University,Taigyuan 030031,China E-mail: zhanglih149@126.com
1 Introduction
The aim of this paper is to show the positive radial solutions of the following(k1,k2)-Hessian system involving a nonlinear operator and gradient:


where N ≥2, G is a nonlinear operator on Λ={G ∈C2([0,+∞),(0,+∞))|, and there exists a constant α >0 such that for all 0 <l <1,G(ls)≤lαG(s)}.
Inspired by the above works, by using the monotone iterative method, we investigate the existence of entire positive bounded and blow-up radial solutions of the nonlinear (k1,k2)-Hessian system (1.1) involving a nonlinear operator. Our results complement the works of many authors([1–15,18–24]),and are also closely related to some recent works by the iterative method ([25–29]) for various differential equations.
2 Main Results
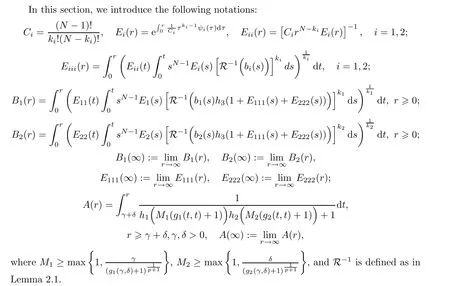

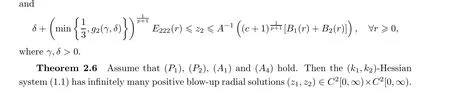
3 Proofs of the Main Results







3.1 Proof of Theorem 2.4

3.2 Proof of Theorem 2.5


3.3 Proof of Theorem 2.6

猜你喜欢
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- THE GENERALIZED HYPERSTABILITY OF GENERAL LINEAR EQUATION IN QUASI-2-BANACH SPACE*
- NO-ARBITRAGE SYMMETRIES*
- O(t-β )-synchronization and asymptotic synchronization of delayed fractional order neural networks
- On the dimension of the divergence set of the Ostrovsky equation
- MAXIMAL L1-REGULARITY OF GENERATORS FOR BOUNDED ANALYTIC SEMIGROUPS IN BANACH SPACES*
- Weighted norm inequalities for commutators of the Kato square root of second order elliptic operators on Rn
