The discrete Orlicz-Minkowski problem for p-capacity

Lewen JI (季乐文)|Zhihui YANG(杨志辉)

School of Science,East China University of Technology，Nanchang 330013，China E-mail : jilewen2008@163.com; yang-zhihui@aligun.com

Abstract In this paper，we demonstrate the existence part of the discrete Orlicz-Minkowski problem for p-capacity when 1 ＜p ＜2.

Key words Convex polytope; Orlicz-Minkowski problem; p-capacity

1 Introduction

The Minkowski problem is a characterization problem for a geometric measure generated by convex bodies， and asks the following: given a finite Borel measure µ on Sn-1， what are the necessary and sufficient conditions on µ so that µ is the surface area measure S(K，·) of a convex body K in Rn? This problem was solved by Minkowski himself for the discrete case at the end of the 19th century. In 1938， Aleksandrov [1] and Fenchel-Jessen [14] independently solved the problem for arbitrary measures by adopting the variational method to transform the Minkowski problem with an optimization problem. This had a strong influence on both the Brunn-Minkowski theory and fully nonlinear partial differential equations for the study of Minkowski problem， because the solution of the Minkowski problem is equivalent to solving a completely nonlinear partial differential equation; for details， see [32].

In recent years， the Orlicz-Brunn-Minkowski theory originated from the work of Lutwak，Yang， and Zhang; see [29， 30]. Haberl， Lutwak，Yang and Zhang proposed in [17] the following Orlicz-Minkowski problem: given a suitable continuous function φ:(0，+∞)→(0，+∞) and a Borel measure µ on Sn-1， is there a convex body K such that for some c ＞0，

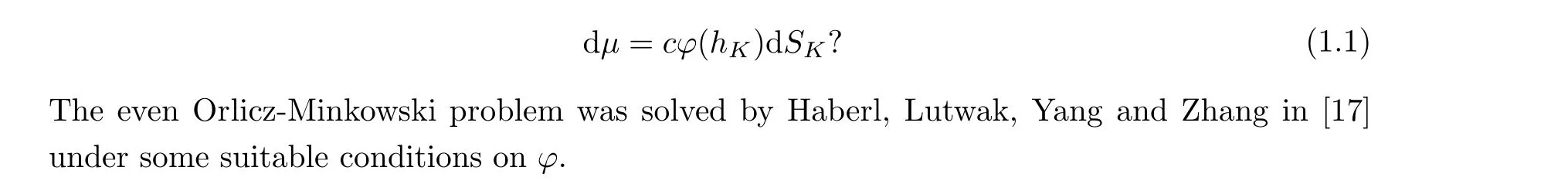
Sometimes， the Orlicz-Minkowski problem is called the LφMinkowski problem， and correspondingly， the Orlicz surface area measure is called the Lφ-surface area measure. The LφMinkowski problem includes the classical Minkowski problem when φ is a constant function and the LpMinkowski problem when φ(t)=t1-p. For the development of the Minkowski problem，see [3–10， 16–19， 22， 25–28， 33， 34， 36–40] and Schneider’s book [32].

Replacing the surface area measure by the p-capacitary measure for p ∈(1，n)， the related Minkowski problem is named the p-capacitary Minkowski problem: under what conditions on a given finite Borel measure µ defined on Sn-1can one find a convex domain (i.e.， the interior of a convex body) whose p-capacitary measure is equal to µ? Jerison in[23， 24]solved the case p= 2. In 2015， Colesanti， Nystr¨om， Salani， Xiao， Yang and Zhang in [12] solved this problem for p ∈(1，2). The normalized (nonlinear) p-capacitary Minkowski problem for all p ∈(1，n)was solved by Akman， Gong， Hineman， Lewis and Vogel [2].

In view of Orlicz-Minkowski problems， Hong， Ye and Zhang in [19] proposed the following question: under what conditions on a given function φ and a given finite Borel measure µdefined on Sn-1can one find a convex domain such that the origin o is in its closure and

Corollary 1.3 Suppose that 0 ＜q ＜1， 1 ＜p ＜2 and that µ is a discrete measure on Sn-1satisfying condition (A2). If a1，a2，...，aN＞0， and u1，u2，...，uN∈Sn-1are not contained in any closed hemisphere， then there exists a polytope P which contains the origin in its interior and c ＞0 such that

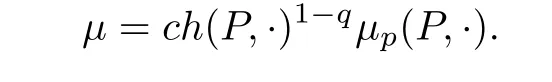
The rest of this paper is organized as follows: in Section 2， we provide some preliminaries about convex bodies and p-capacity. In Section 3，we state the extremal problem to the Orlicz-Minkowski problem. In Section 4， we complete the proof of the main result.

2 Preliminaries

In what follows， we collect some basic facts on the theory of convex bodies and p-capacity(see also Schneider’s book [32]).

Let Knbe the set of convex bodies (compact convex subsets with nonempty interiors) in Rn， and let Knobe the set of convex bodies containing the origin in its interior，denoting by Bnthe unit ball. Int(K) and bd(K) are the interior and boundary， respectively， of a set K. The support function hKof convex body is defined by

Obviously， for P ∈P(u1，u2，...，uN)， P has at most N facets， i.e.， (n-1) dimensional faces，and the outer normals of P are a subset of {u1，u2，...，uN}. We write PN(u1，u2，...，uN)as the subset of elements P(u1，u2，...，uN) such that a polytope P ∈PN(u1，u2，...，uN) if P ∈P(u1，u2，...，uN) and P have exactly N facets.

2.2 Basic facts on p-capacity

Letting 1 ＜p ＜n， recall that the electrostatic (or Newtonian) p-capacity Cp(Ω) of a compact set Ω is defined by

3 An Extremal Problem to the Orlicz-Minkowski Problem

In this section， suppose that a1，a2，...，aN(N ≥n + 1) ∈R+， that the unit vectors u1，u2，...，uN∈Sn-1are not contained in any closed hemisphere， and that P ∈P(u1，u2，...，uN). We now define the function Φφ(P，·):P →R by

For brevity， let x(t)=xφ(β(t)Pt).

Lemma 4.3 Under the assumptions of Lemma 3.1，if the n-dimensional polytope P solves problem (4.1) and xφ(P) = o， then P has exactly N facets， the normal vectors of which are u1，u2，...，uN.