基于改进t分布混合模型的路面裂缝图像分割方法研究
2022-08-25段明义李祖照崔奥杰
段明义,李祖照,崔奥杰
(1. 郑州工程技术学院 信息工程学院,河南 郑州 450044; 2. 广西交科集团有限公司,广西 南宁 530007)
0 引言
近20年来,伴随着我国交通事业的发展,汽车保有量也随之迅猛增长,人们对行车的要求也在不断转变,尤其体现在安全性、经济性以及舒适性等方面的需求。这使得路面养护变得重要和紧急[1]。目前,对于公路状况的检测手段,国内外常见的是人工方法和半自动方法,这些方法的缺点是效率低、强度大以及准确性不够等。道路在投入使用后,随着使用年限的增长,会产生不同程度的裂缝,裂缝是评价公路质量的一个重要指标。裂缝的类型和裂缝的程度关系后期的维护修补策略[2]。相对于采用人工检测的方法,利用计算机技术进行裂缝检测具有高效、非接触、精度高等优点,图像分割是其中最常用到的技术之一。
一种常用的图像分割方法是K-means聚类划分[3],原理简单、易实现,缺点是参数值的设置需要事先由人工来完成。同时,该方法在含噪声图像上运行效果欠佳[4]。因此,实际应用中,一般需要对标准K-means聚类进行优化,然后再使用其进行分割。本研究采用花粉算法(Flower Pollination Algorithm,FPA)[5]来对其进行改进,该算法参数少,易实现。数理统计中,比较常用的数据模拟模型是高斯模型[6],随着待模拟数据量的增加,可以采用多个高斯模型加权的形式来构造模型进行模拟,即高斯混合模型(Gaussian Mixture Model, GMM)[7]。学生t分布(Student’st-distribution)[8]是另一个常见的数据模型,具有较长的尾部,更适合用来处理裂缝图像,因此,本研究采用其来代替高斯分布,多数据模拟的情况采用t分布混合模型(t-distribution Mixture Model, TMM)[9]。
在本研究中,针对公路裂缝图像的特点,以t分布混合模型为基础,对其在参数优化和求解方面进行改进,本研究方法为K-means改进t混合模型法(K-means Improvedtdistribution Mixture Model,KITMM)。
1 方法
1.1 学生t分布
学生t分布的概率密度函数为:
(1)
式中,v为自由度参数,Γ(·)为Gamma函数。根据文献[10]可知,通过调整自由度参数v,可以将t分布调整为柯西分布或高斯分布,从而实现自适应变异。
1.2 聚类算法
1.2.1K-means算法
对于含有N个数据点的裂缝图像,这N个数据点分别为X={x1,x2,…,xN},其中xi表示像素灰度值。K-means算法利用预设的聚类个数值K,将裂缝图像自动划分为K个部分M1,M2,…,MK,每个部分称为一个子集或者聚类,其中心分别为c1,c2,…,cK。
其目标函数如式(2)所示:
(2)
式中x为来自裂缝图像子集Mj的样本。
当目标函数取得最小值时,利用式(3)计算并更新各聚类中心c1,c2,…,cK。
(3)
式中,cj为子集中心,Nj为子集样本个数。聚类算法主要采用迭代的方法,逐步更新子集位置,直至不再更新或者满足预设迭代次数为止。
虽然原理简单且易实现,但标准K-means缺点也很明显,每次运行算法前都要进行参数设置,在有些情况下,这一步不容易实现,本研究对此采用花粉算法改进提高。
1.2.2 花粉算法
自然界中的显花植物,经过亿万年的演化史,已经发展出来一种独特的、行之有效的授粉方式。花粉算法(Flower Pollination Algorithm,FPA)[5]主要采用全局和局部两种授粉方式,两者之间可以通过参数p控制转换的概率,p∈[0,1]。
鉴于植物与动物的不同,其活动性基本为0,授粉大部分发生在局部区域,即局部授粉在总体授粉活动中占很大比例p。根据文献[5],p=0.8。设种群规模为N,i∈[1,N],X代表种群中的花朵。
全局授粉方式为:
(4)
(5)
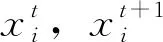
(6)
(7)
局部授粉方式为:
(8)

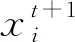
(9)
利用式(10)~(11)进行更新:
(10)
(11)
式中,fit为算法求解过程中使用的适应度函数。算法运行结束时,输出g*,fit(g*)。
实际运行中,FPA算法前期易落入局部最优,后期逼近最优点的速度较慢。本研究采用改进方法,该方法主要借鉴文献[12],对花粉状态Xi=(xi1,xi2,…,xin)进行自适应t分布变异,定义如下:
(12)
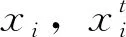
本研究首先运行FPA算法获得一个初始解,然后以该解为输入,运行K-means算法,发挥其特性进行局部寻优,聚类结束,求取一个最优解。然后将该解作为下一步混合模型参数求解的初始值。
1.3 t分布混合模型
学生t分布(Student’st-distribution)是除高斯分布之外另一常用的分布,它较高斯分布具有更长的尾部,更适合用来模拟裂缝图像。
多维(p维)学生t分布可以用式(13)表示:
(13)
式中,δ(x,μ;Σ)=(x-μ)TΣ-1(x-μ)。采用与高斯模型相似的方法,将多个学生t分布模型进行加权,即学生t分布混合模型[9],如式(14)所示。
(14)
式中πk为混合系数。
有限混合模型中未知参数的求解有很多种方法,本研究中采用EM算法[13]。
E步:
(15)
(16)
M步:
(17)
(18)
(19)

(20)

重复执行式(15)~(16)的E步,以及式(17)~(19)的M步,直到满足结束条件,即可求出混合模型的参数,从而确定该模型。利用贝叶斯公式,可计算每个像素的后验概率以确定其所属类别,完成最终分割过程。
1.4 算法流程图
算法整体流程如图1所示。

图1 算法流程图
2 试验结果与分析
2.1 试验环境及评价准则
试验环境由软件和硬件两方面组成,软件方面主要为Matlab 2012b,硬件方面主要为8 GB内存,Intel 3.2 GHz CPU以及2T硬盘。试验图像主要由合成图像以及实际公路裂缝图像组成。合成图像由Photoshop软件生成,实际裂缝图像由道路养护人员现场采集。
试验部分主要通过以下两个指标值来对算法性能进行衡量:误分率(MCR)[14]和概率随机(PR)索引[15]。
MCR=Ne/N×100%,
(21)
式中,MCR取值位于[0,1]区间,其值越小表示分割结果越好。Ne为误分像素数;N为像素总数。
概率随机索引PR定义为式(22)。
(22)
式中cij=1表示在测试分割结果Stest中像素i和j属于同一聚类,否则cij=0。pij的值可以利用式(23)定义的样本均值估计得到。
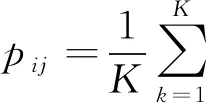
(23)
式中K表示基准集的个数,是一个恒等函数,当像素i和j属于基准集中同一聚类时,它的值等于1,否则它的值为0。PR∈[0,1],值越大表示分割效果越好。
2.2 结果与分析
试验部分主要在合成[16]和实际两类图像上进行分割,以对本研究算法的性能进行验证。
对比算法包括TMM[9],SMM-AM[17],SCSMM[18],本研究方法为KITMM。
试验方案为:首先在噪声污染后的合成图像上运行本研究算法以测试其有效性,然后将该算法在真实裂缝图像上运行,同时运行对比算法以测试其优越性。
2.2.1 合成图像试验结果与分析
图2(a)~(c)分别为合成图像原图以及含噪声图像,图2(d)和(e)为分割结果。

图2 合成图像分割结果
图2结果显示,本研究方法在含噪声图像上也能够实现分割,这说明算法具有抗噪性。图3为在不同噪声水平下分割算法鲁棒性测试结果。

图3 分割算法鲁棒性测试结果
图3结果显示,算法分割误差随着噪声的增大而增加,说明噪声对算法有影响,但整个曲线增幅不大,说明算法抗噪性好。
2.2.2 实际路面裂缝图像试验结果与分析
为进一步测试本研究算法的有效性,取4种公路裂缝样本,如图4(a1),(b1),(c1),(d1)分别运行各对比算法,进行分割。其中图4(a1),(b1)为单条裂缝,图4(c1),(d1)为网状裂缝。
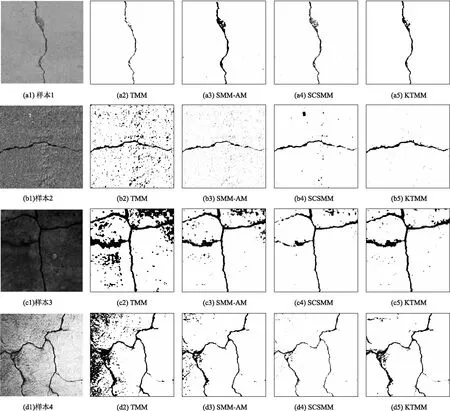
图4 实际裂缝图像分割结果对比
图4结果显示,4种算法都能够将公路裂缝部位分割出来,但分割效果不同。传统t混合模型(TMM)和自适应均值滤波t混合模型分割的结果中,除了裂缝本身,还含有一些其他的背景信息。样本1因为背景比较单一,该问题不是很突出。样本2中表现比较明显,样本3结果中,TMM方法具有较多背景信息,SMM-AM方法背景信息主要集中在图形上部区域,样本4中主要集中在左侧区域。这些部位,因为灰度值较大,被保留了下来。基于马尔科夫随机场的t混合模型分割结果,与其他3种算法分割结果相比,对裂缝部位保留得最好,且其他部位剔除得最干净,但其分割出来的裂缝部位,不够清晰,存在断裂现象,比如样本2的右侧部分,样本3的左侧两支裂缝,以及样本4的中部和下部,都存在断裂。本研究方法(KITMM)分割的结果,优于其他3种算法,在最大限度保留裂缝部位信息的同时,也能够分割出清晰的裂缝图像。定量结果如表1所示。
表1结果表明,从评价指标MCR和PR来看,本研究算法各图像分割结果都较优。时间指标表明本研究算法处于劣势,原因在于对分割算法的改进增大了算法本身的复杂度,从而消耗了更多的运行时间,也即是在提高分割效果的同时,增加了时间成本。
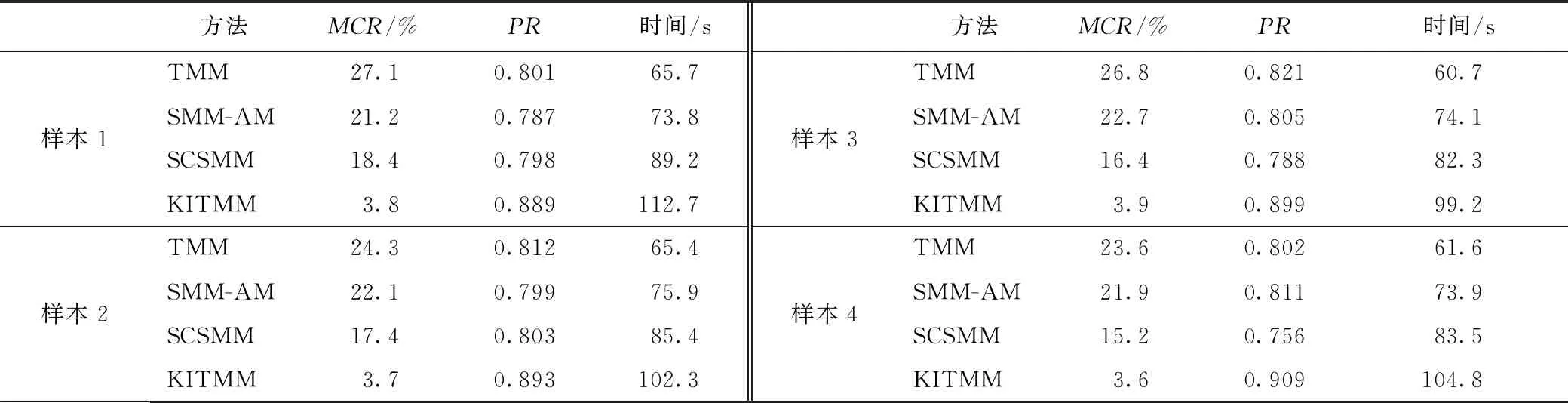
表1 定量评估结果
3 结论
在分析公路裂缝图像特点之后,本研究基于t分布模型构造一种图像分割方法,主要用来实现公路裂缝图像分割。该方法主要在模型初始参数计算、模型最终参数求解等方面进行改进提高分割效果。试验部分构造了软硬件环境,仿真图像和实际公路裂缝图像测试结果表明改进算法抗噪性强,精度高并且分割效果好。
