阶梯圆柱壳屈曲问题的哈密顿方法
2022-08-25赖安迪赵建宇周震寰徐新生
赖安迪,赵建宇,周震寰,徐新生
(大连理工大学 工程力学系和工业装备结构分析国家重点实验室,辽宁 大连 116024)
0 引言
现代工程中,阶梯圆柱壳结构应用非常广泛,分布式的刚度有助于减轻整体结构重量,大大增强薄壁结构的适用性.然而,若结构中存在材料缺失和不均匀的缺陷,会导致壳的整体应力分布发生显著变化,复杂的屈曲形式也给结构的稳定性评估带来挑战.圆柱壳作为传统的结构之一,已被众多学者深入研究,在REDDY J N[1]和沈惠申[2]的著作中对此有详细的概述.早期圆柱壳轴压屈曲的实验与理论预测值之间较大的差异,激励了许多学者对其进行研究.目前普遍认为在制造或使用过程中产生的缺陷是导致圆柱壳承载能力降低的最重要原因,细微的缺陷或壳体厚度不均匀也可能导致圆柱壳的临界荷载和屈曲变形发生很大改变.乔丕忠等[3]对圆柱壳稳定性问题的研究进行了详细概述,其中包括了缺陷对圆柱壳屈曲影响的重要研究进展.张东等[4]对简支边界条件下纵横加筋圆柱壳在轴压和温度载荷联合作用下的屈曲问题进行了理论分析,给出临界屈曲载荷解析表达式.吴双华等[5]为提高变刚度圆柱壳的临界载荷,提出两种铺丝方案并运用径向基函数模型优化了方案中的相关参数.桂夷斐等[6]建立了阶梯圆柱壳径向位移控制方程,得到应力波反射后的动态屈曲分叉条件.结果表明,阶梯圆柱壳更容易发生轴对称屈曲.胡服全等[7]采用专用的轴压屈曲试验平台,扫描了壳体屈曲的三维实际形貌.潘力等[8]采用线性屈曲分析模块,模拟凹陷位置、凹陷半径及深度对圆柱壳轴向临界载荷的影响,得出球冠状凹陷对圆柱壳轴向临界载荷的影响规律.结果表明:凹陷位置变化使得轴向临界载荷近似呈现正弦规律,凹陷半径增加使得轴向临界载荷减小,且临界载荷变化率逐渐降低.陈志平等[9]从理论、实验和数值模拟等几个方面,介绍了圆柱壳轴压屈曲研究进展,总结了等壁厚和不同类型变壁厚圆柱壳轴压屈曲临界载荷的求解方法.万福腾[10]采用实验研究与有限元数值模拟相结合的方法,对纵向加筋薄壁圆柱壳的轴压屈曲问题进行研究,结果表明:加强筋的数量、截面积和高宽比对薄壁圆柱壳轴压屈曲临界载荷的影响较显著,而圆柱壳径厚比和高径比无显著影响.曹国伟[11]使用多种方法,详细研究了任意变壁厚和开孔这两种因素对圆柱壳轴压屈曲临界载荷的影响.XU X S 等[12]建立了圆柱壳在轴向压缩冲击载荷作用下屈曲问题的哈密顿对偶方程,并对方程进行了数值求解.结果表明,壳体的屈曲可分为短波屈曲和长波屈曲两类.SUN J B等[13]在哈密顿体系下研究了圆柱壳在外压、扭转和轴压联合作用下的屈曲行为,同时考虑了对称和非对称边界条件.结果表明,对于较长的圆柱壳,外压对屈曲的影响比轴压显著.此外,释放轴向约束会显著降低屈曲载荷和周向波数.
在哈密顿体系下,建立多区域的哈密顿方程,并利用连续性条件及边界条件,求解轴压作用下阶梯圆柱壳的特征值屈曲问题,并给出缺陷诱导壳体局部屈曲现象的解析解描述.作为一种理性求解法,具有显式和简洁的特点,并且可适用于阶梯区域厚度较大突变、局部力学量急剧变化的情况.
1 基本理论
考虑如图1的薄壁圆柱壳模型,长为l,半径为r,厚度为h,弹性模量为E,泊松比υ.壳体受轴压N0作用.阶梯区域为x1≤x≤x2,厚度为h0.取圆柱坐标系(r,θ,x),径向位移w.圆柱壳的中面应变与中面位移关系为
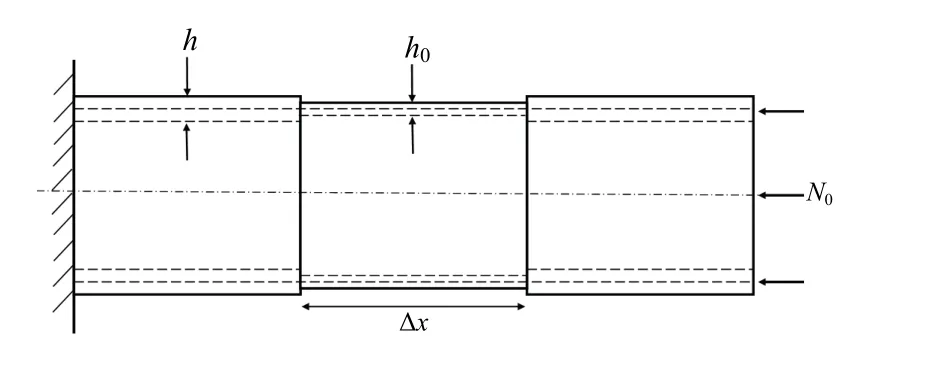
图1 受轴压的阶梯圆柱壳Fig.1 stepped cylindrical shell subjected to axial pressure
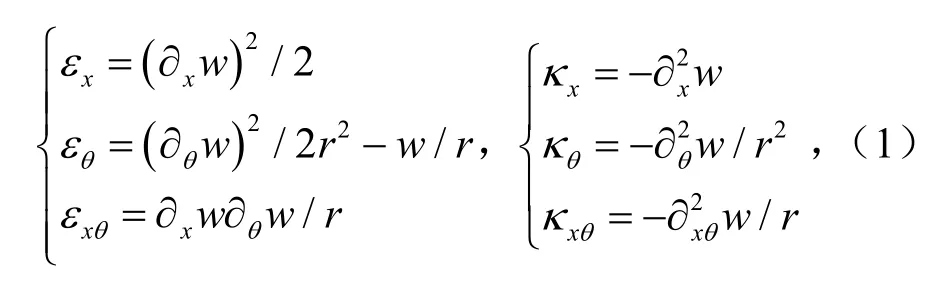
内力与中面应变的关系为
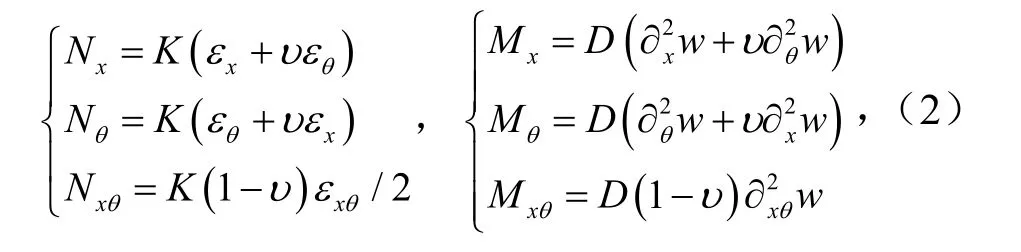
式(1)~式(2)中,抗拉伸刚度为K=Eh/(1-υ2),抗弯曲刚度D=Eh3/12(1 -υ2).假定壳体发生屈曲时,横截面承受均匀压载荷.壳体的应变能,即拉格朗日函数表示为
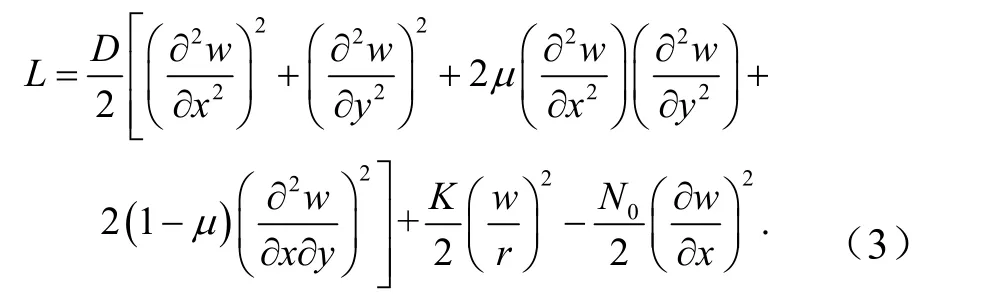

2 哈密顿系统
用θ坐标模拟时间坐标,记F′=∂xF和,定义原变量q=[w,φθ]和对偶变量.其 中φθ=-w˙ 为θ方 向 的 转 角,为θ方 向 的 等 效 剪 力,为θ方向的等效弯矩.对拉格朗日函数进行勒让德变换,哈密顿函数为
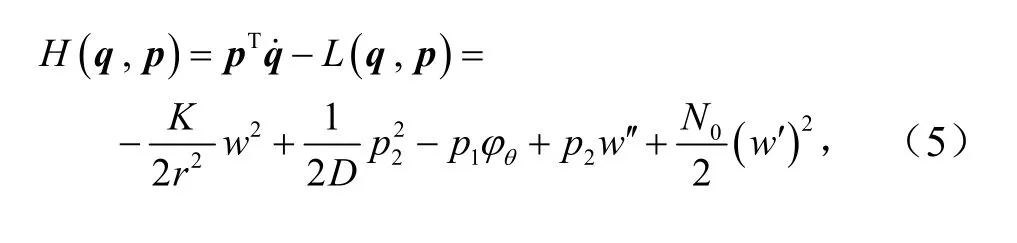
由
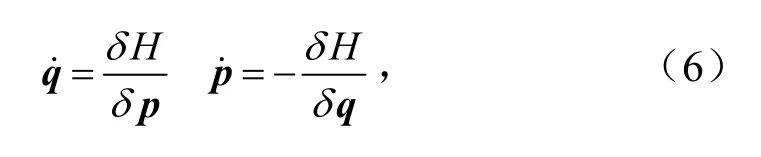
可建立哈密顿方程 =˙Hψψ,矩阵形式为
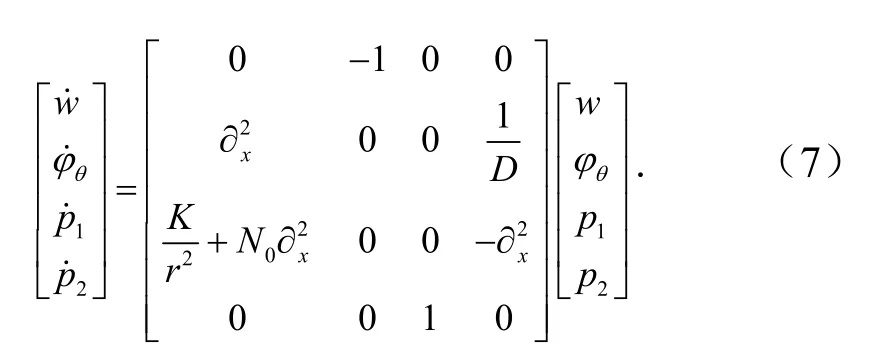
方程(7)为线性哈密顿体系,可适用广义分离变量法ψ(x,θ) =φ(x)euθ,注意到圆柱壳环向的周期性条件ψ(x, 0 ) =ψ(x,2π),可得u= in,其中n=±0 ,1,2····.根据微分方程组的理论,哈密顿方程的解为
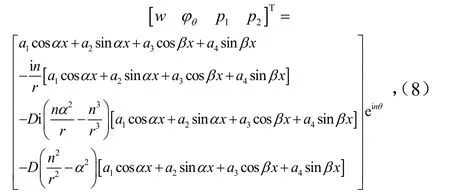
式中,
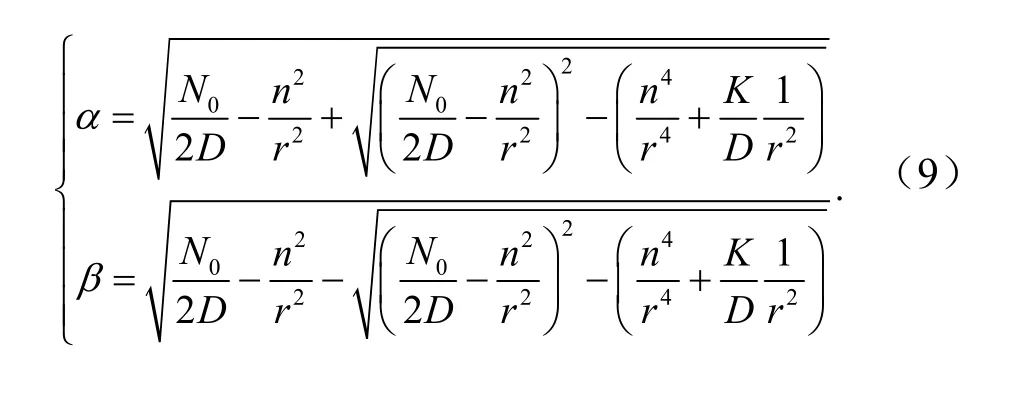
对于阶梯区域x1≤x≤x2,刚度D变为D′ 后,α→α′,β→β′.3个区域的径向位移为
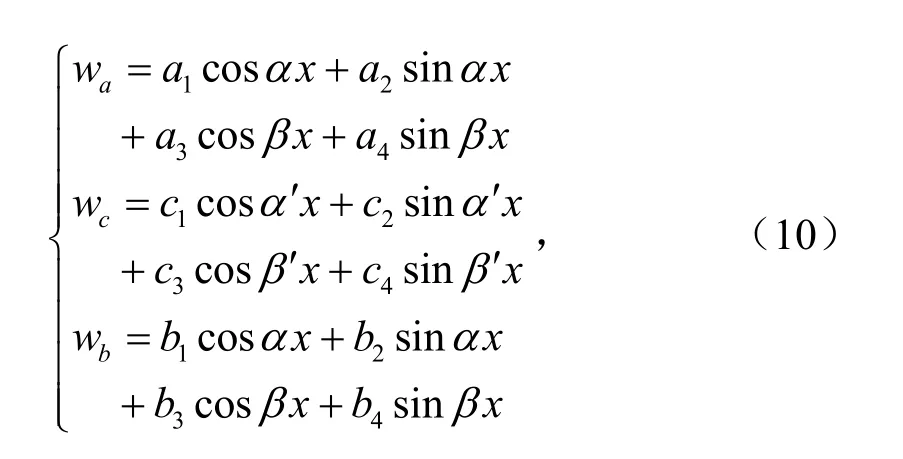
不同区段哈密顿方程的解可表示为
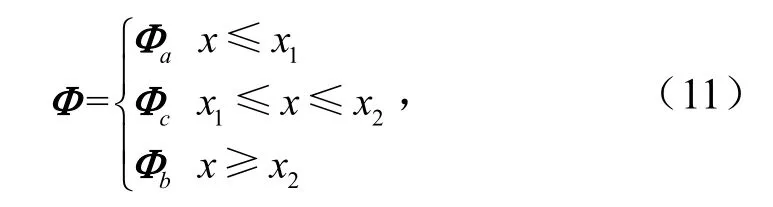
式中,
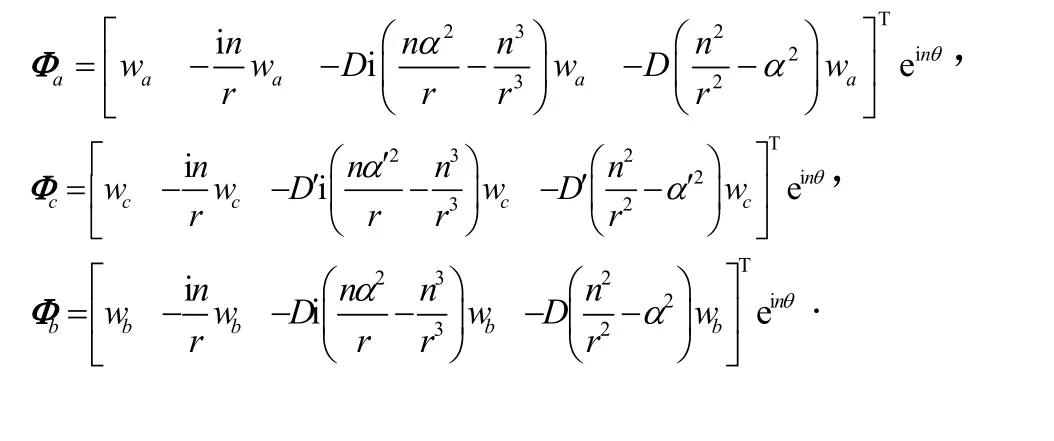
3 边界条件及连续性条件
阶梯圆柱壳的解(11)有12个未知系数,需要结合边界条件及连续性条件求解.对于两端固支圆柱壳,边界条件为
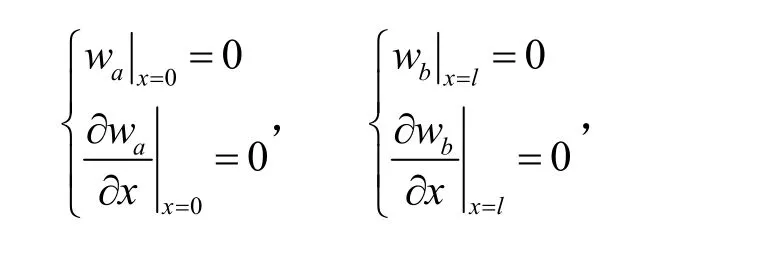
连续性条件要求在阶梯变化处有
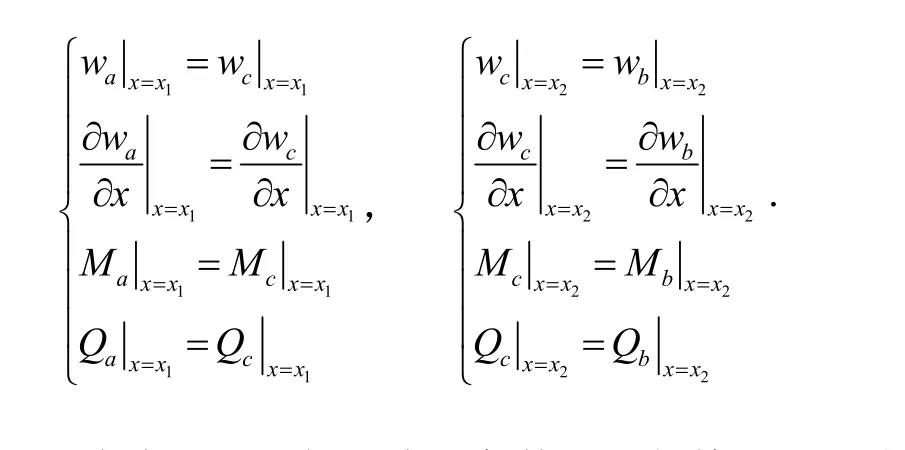
将式(11)代入边界条件,可得特征方程为
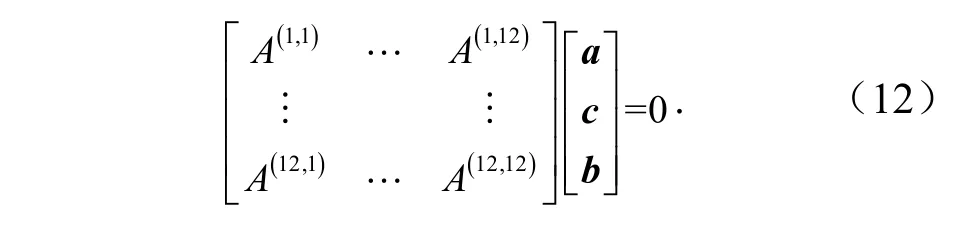
阶梯圆柱壳屈曲临界载荷的求解问题,转换成齐次方程特征值问题,令系数矩阵行列式
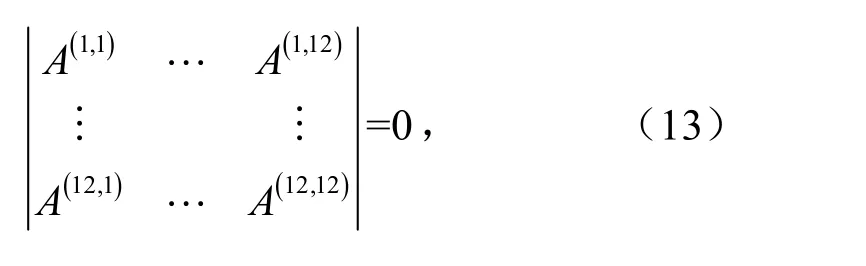
即可求解N0,进而得到特征向量a,b,c,可确定阶梯圆柱壳的屈曲模态.
4 数值结果及分析
计算两端固支阶梯圆柱壳的轴压屈曲,取l=5 m,r=1 m,h=0.02 m,泊松比 0υ= ,定义无量纲屈曲系数k=N0/D和阶梯区域与外部区域的厚度比ε=h0/h,阶梯区域中心位置为x0,宽度为Δx.计算x0=0.5l、Δx=0.1l时,不同ε下的屈曲系数,并与有限元进行对比,结果见表1.从数值上可以看出,2种方法所得结果接近,相差不超过1.1%,且都显示出了临界载荷对局部材料的缺失的敏感性,少量的厚度改变可导致屈曲载荷显著下降.
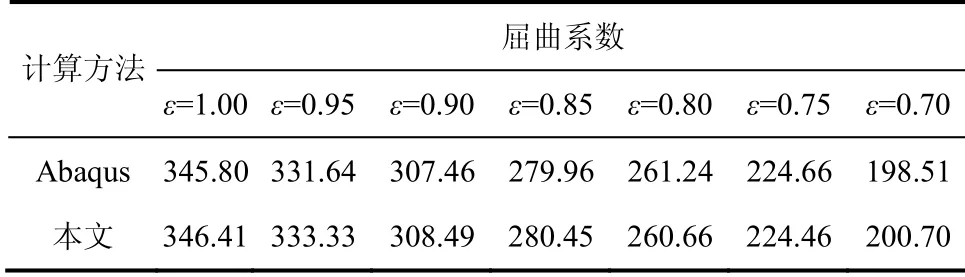
表1 不同厚度比ε下的屈曲系数Tab.1 buckling coefficients of different thickness ratios ε
图2为宽度Δx=0.2l时,不同厚度比ε下的圆柱壳的最低阶屈曲模态,从图2可以看出,随着阶梯区域材料的缺失,材料屈曲的范围越来越集中在局部.相比之下,阶梯区域以外的壳体屈曲不明显.ε=0.90时,屈曲的范围已经大部分集中在阶梯区域段.并且,随着厚度比ε进一步下降,阶梯区域与外部的分界愈发明显.整个结构的屈曲形式从整体屈曲转变为局部屈曲.
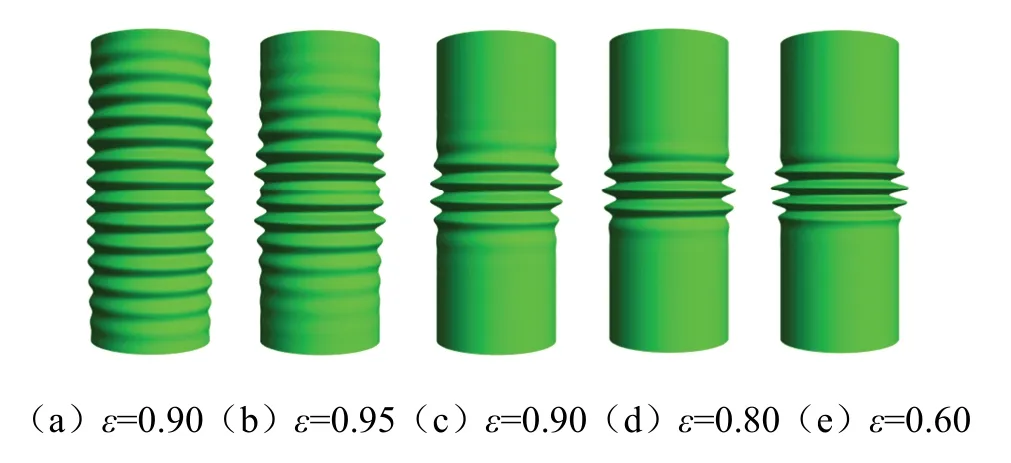
图2 不同厚度比下的屈曲模态Fig.2 buckling modes at different thickness ratios
图3 为宽度Δx=0.2l时,厚度比ε=0.60时阶梯圆柱壳的前5阶屈曲模态.n=0时为轴对称局部屈曲;n>0时结构的屈曲模态为非轴对称局部屈曲形式;n=2时壳体呈现出局部扭曲的模态,并且随着n值越大,相应的屈曲载荷会逐渐增大,局部环向的屈曲波纹数会逐渐增多.
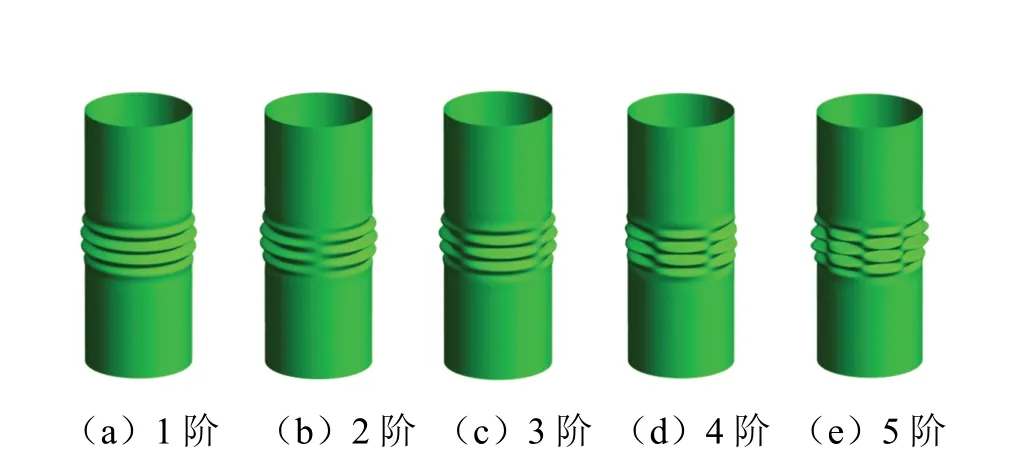
图3 前5阶局部屈曲模态Fig.3 buckling modes of first five steps
通过分叉条件求解x0=0.5l、ε=0.90时,不同阶梯宽度下的屈曲系数,结果见图4.从图4可知,缺陷尺寸不同,相应的屈曲系数也有很大不同.当阶梯区域很窄时,不管区域深度如何,屈曲系数都与完整圆柱壳的数值接近,但随着宽度逐渐增大,屈曲载荷迅速下降.从图4中还可以看出,ε越小,结构的临界载荷对阶梯区域的宽度Δx越敏感.在ε=0.90的情况下阶梯区域宽度增加至壳体长度的4%,相比于完整圆柱壳,屈曲载荷仅下降了不到3%.而在ε=0.60情况下,阶梯区域宽度同样增加至壳体长度的4%,相比于完整圆柱壳,屈曲载荷下降了35%.
图5 为Δx=0.2l时,屈曲系数随阶梯区域的中心位置x0的变化情况.从图5中可以看出,当材料缺失的区域靠近端部时,由于端部的支撑作用,屈曲系数会有所上升,如ε=0.60情况下,靠近端部,壳体的抗屈曲能力增加了12%.在远离端部的大部分区域,屈曲系数变化不明显.因此在实际工程中,在阶梯区域靠近端部时,应考虑端部对临界载荷的影响.而在远离端部的大部分区域,壳体的临界载荷对位置不敏感,评估结构只需考虑缺陷区域的尺寸大小对临界载荷的影响.
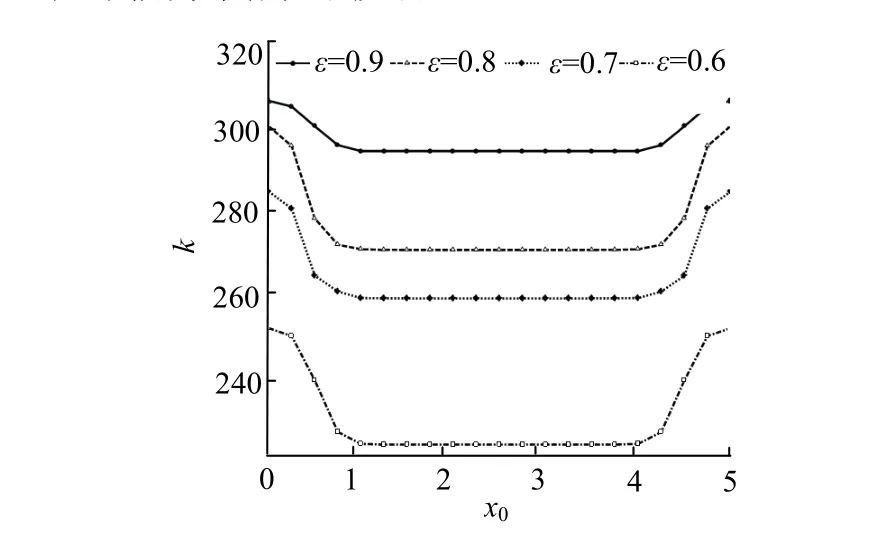
图5 屈曲系数随阶梯区域中心位置变化Fig.5 buckling coefficient varies with central position of stepped regio
5 结论
在哈密顿体系的框架下,提出了一套精确求解阶梯圆柱壳屈曲问题的辛方法.数值算例对影响圆柱壳临界荷载和屈曲模态的主要因素进行了详细分析,揭示了阶梯区域的深度、宽度、位置等因素对圆柱壳屈曲行为的作用规律,主要结论如下.
(1)阶梯区域的材料缺失会降低圆柱壳的抗屈曲能力,当阶梯区域的深度或宽度增加时,壳体的抗屈曲能力会迅速下降.
(2)随着阶梯区域的深度和宽度不断增加,壳体屈曲模式会由整体屈曲转变为局部屈曲.此时继续增加阶梯区域的宽度,临界荷载变化不大,但继续增加阶梯区域的深度,临界荷载还会继续下降.
(3)当阶梯区域靠近壳体端部时,由于边界的支撑作用,临界荷载会有所上升,但在远离端部的大部分区域,壳体的临界载荷对阶梯区域位置不敏感.因此评估结构的稳定性时应重点考虑阶梯区域深度与宽度两个因素,并考虑局部屈曲对结构整体的影响.本文方法具有显式和简捷的特点,可用于阶梯圆柱壳的稳定性评估.
