仿生材料结构取向对力学性能的影响
2022-08-25袁文玺张泽辉
王 昊,袁文玺,叶 梯,张泽辉
(1. 沈阳大学 机械工程学院,辽宁 沈阳 110000;2. 成都城电电力工程设计有限公司 输电设计部,四川 成都 610000; 3. 中国民用航空飞行学院 航空工程学院,四川 成都 610000)
0 引言
人类社会的进步伴随着材料的生产和技术的革新,材料的每一次发展与突破都推动了社会生产力的发展[1].复合材料是材料科学领域的研究热点.近年来学者们通过使用各种先进的实验设备和方法,取得了令人瞩目的研究成果[2-3].对于仿生领域,国内外学者们很早就开始了研究,并且在结构仿生、过程仿生和仿生设计方面都取得了一定的进展.仿生材料是模仿生物各种特点研制而成,很好地将材料与仿生概念结合在一起,是一种建立在自然界原有材料、人工合成材料、有机高分子材料基础上的可设计智能材料[4].自然界中物种丰富,生物材料具有形态多样性,大多数生物材料本质上是可以看作是一定尺度下的复合材料,且至少包含具有不同力学性能(尤其是刚度)的两相材料[5].骨骼的组成可以认为是两相组合的例子.图1为微观尺度下骨骼的结构层次[6],图1(b)是图1(a)的局部较大,图1(c)是图1(b)的局部放大.骨骼的宏观排列有的是致密的或松质的,有的是海绵状的或松质的.致密骨由包围和保护血管的骨单元组成,骨单元具有层状结构,每个单独的板层由排列成几何图形的纤维组成.

图1 微观尺度下骨骼的层次结构Fig. 1 hierarchical structure of bone at micro scale
在生物学中,层次系统是具有多个尺度的结构,其中层次结构由相同的重复几何组成.许多生物系统具有分层的界面和关节结构,它们承受和传递载荷、吸收能量、适应生长、呼吸、运动.LI Y N等[7]通过建立弹性确定性复合材料力学模型,定量地研究了结构层次对缝合界面刚度、强度和失效的影响,并指出当其它结构几何和参数在生物学上具有挑战性时,自然界中的生物材料有明确的功能序列和有效的几何结构策略,可以在有限的材料选择前提下获得不同的性能.经过长时间的进化和演化,自然界中贝壳、牛角、骨头、龟壳等一类生物材料具有优异的力学性能,与块体材料相比,该类生物材料的优异力学性能主要源于其基本组成单元,是通过有序的层状结构构筑而成[8].研究材料结构取向对层状仿生材料力学行为的影响,对设计力学性能优异的仿生复合材料具有重要的意义.
近年来学者对仿生复合材料的增韧机制和微观力学性能方面进行了大量研究.侯祥龙等[9]研究贝壳珍珠层“砖墙”式微观结构,对微结构组合方式进行优化设计,利用光固化3D打印技术制备了具有“砖墙”构型的仿贝壳珍珠层及其结构优化的复合材料,探究了这类复合材料在准静态拉伸条件下对力学行为的影响.材料力学性能的提高常常受到不同参数之间一系列矛盾关系的制约,例如强度与损伤容限、机械刚度与稳定性、柔度[10].寻求材料学科与力学学科的综合解决方案来避免这种冲突是可取的,这也是人造材料系统中的一个关键点和难点.LIU Z Q等[11]从材料和力学的角度出发,认为仿生材料在变形过程中,适应性结构的重新定向是多种生物复合材料的一种运行机制,这种机制不仅是一种被动反应,能够提高灵活性,同时也提供一种有效增强刚性、坚固性、机械稳定性和损伤容限的手段.生物体善于通过装配具有空间变化的机械性能保护表面,可通过制造功能梯度材料来抵抗接触变形和损伤.尽管目前学者对生物材料的增韧机制和微观力学性能进行了大量研究,但微观结构取向对力学性能的影响研究较少.
从实验角度研究生物复合材料需要精密的仪器设备,消耗量大,时间周期长,相比之下,计算机仿真具有灵活性大,不受实验条件的限制,研究结果可视化的优势[12].因此,选择有限元模拟方法,进行两相仿生复合材料力学性能的分析,建立两相生物复合材料微观模型,并将计算结果与理论模型结果进行对比,研究仿生材料的结构取向对刚度的影响,为仿生复合材料性能的探索提供一定思路和借鉴.
2 两相仿生复合材料模型
2.1 模型描述
为探索两相生物材料的结构取向对其力学性能的影响,以贝壳的微观结构为研究对象,从复合材料角度出发,建立不同角度下两相仿生材料力学模型,见图2.

图2 取向角不同的两相仿生材料的力学模型示意Fig. 2 mechanical model signal of two-phase biomaterials with different orientation angles
两相仿生材料力学模型是由软相A和硬相B两部分组成的二维模型,软相A充当具有柔韧性有机物或弱界面,而硬相B主要以矿物或仿生材料中的亚结构成分,该模型能够描述广泛的两相仿生材料.沿模型的水平方向施加载荷,θ表示结构取向,当θ= 0o时,如图2(a)为并联仿生复合材料模型,当θ= 90o时,如图2(c)为串联仿生复合材料模型,通过变换角度可以得到不同取向下仿生复合力学模型.为简化分析,假设软相和硬相材料都满足均匀性和各向同性,而不考虑其内部复杂性.VA和VB分别为软相和硬相的体积分数,且满足VA+VB=1.两相仿生材料有限元模型建立过程中使用有限元软件Abaqus.如图2所示,建立两相生物材料有限元模型,通过图2(d)连接约束(Tie)进行绑定,采用分析步(Static/General),有限元模型采用左侧简支,右侧施加位移载荷.
2.2 方法验证
基于复合材料力学可以获得仿生复合材料串并联模型的理论解[13],生物复合材料的表观弹性模量,可以根据复合材料在等应变和等应力状态下的规则进行简单描述.
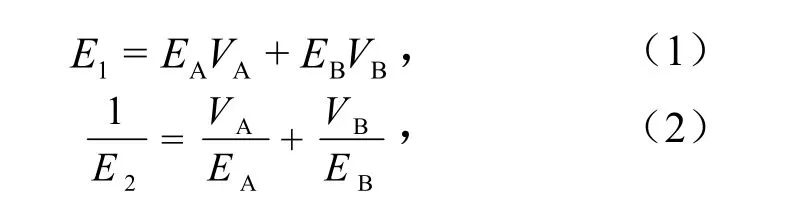
式(1)、式(2)中,E1和E2为不同方向的弹性模量,GPa;EA和EB分别为软相A和硬相B的弹性模量,GPa;根据文献[13]提出任意取向仿生结构弹性模量EB理论模型,可以获得沿任意取向角的表观弹性模量为
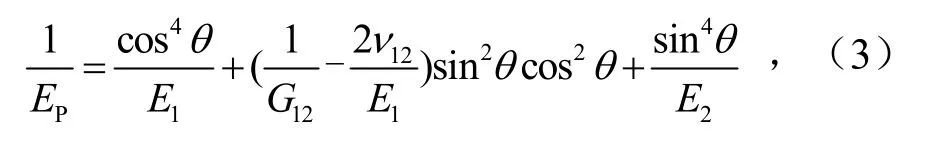
式中,G12为复合材料的剪切模量,MPa;θ为取向角,°;υ12为复合材料的泊松比.
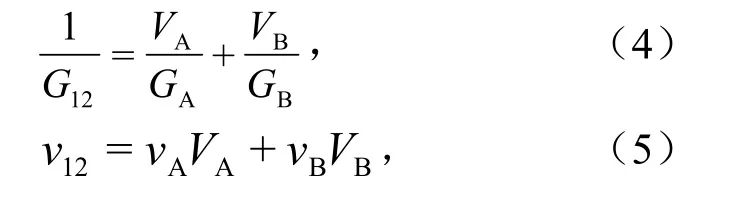
式(4)~式(5)中,GA、GB分别为软相和硬相的剪切模量,MPa;vA、vB分别为软相和硬相的泊松比[11].
通过式(5)得到复合材料的弹性模量为
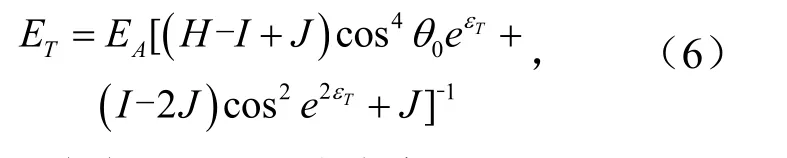
式中,θ0为取向角,°;εT为应变,εT∈[0,lnθ0].
式(6)中H、I、J分别为
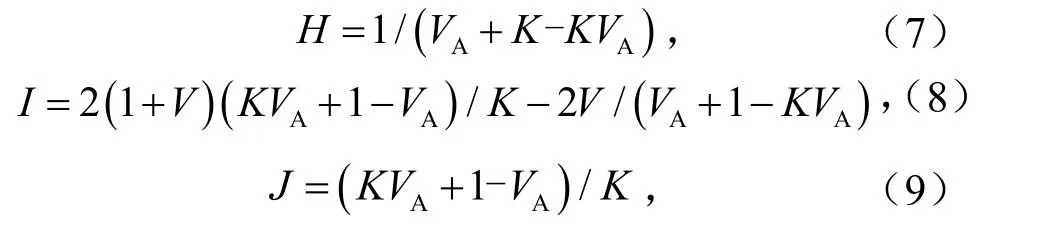
式(7)~式(9)中,V为体积mm3;K为硬相和软相的弹性模量之比.
3 数值结果与讨论
为了与理论模型一致,有限元模型中软相和硬相采用相同的泊松比0.3,有限元模型长宽分别为100 mm和50 mm,模型左边固定不动,右边施加了位移载荷,材料属性取自天然贝壳[14].硬相弹性模量为60 GPa,软相弹性模量为3 GPa,当K等于10时,硬相体积分数为VB等于0.6.通过Abaqus软件分析,提取相关应力和应变的数据,计算不同取向下的弹性模量,本结果与理论数据比对见表1,本结果与文献[13]结果的误差为7%,个别数据点计算误差偏大,但整体不超过20%,充分验证了模型的有效性.
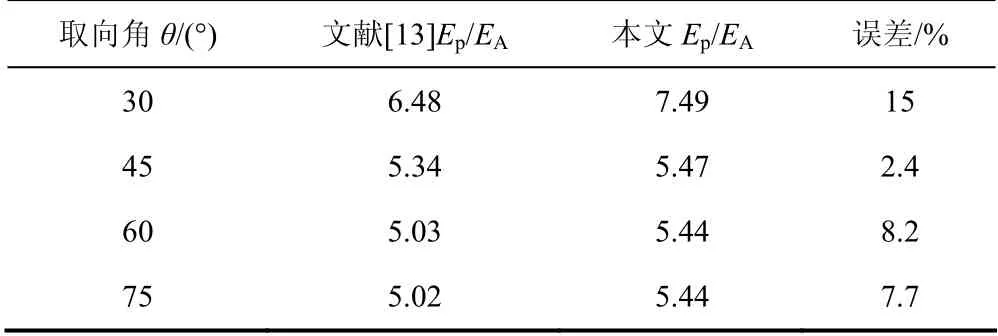
表1 取向角所得结果与参考文献结果对比结果Tab. 1 comparison of analog computation results and reference results
选取向角为30o、45o、60o、75o,并建立两相仿生复合材料模型,有限元模型对应单元数分别为10 992、22 916、25 401、23 134,对应节点数分别为8 902、19 883、22 001、19 601.从Abaqus中提取数据,使用Origin绘制不同取向角的应力-应变曲线,见图3.
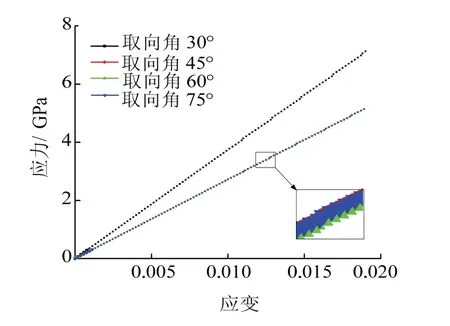
图3 不同取向角的应力-应变关系Fig.3 relationship of stress-strain with different orientation angles
由图3可知,随着仿生复合材料取向角的增大,在相同体积分数和相同材料参数下生物复合材料的弹性模量逐渐减小,这是结构取向对材料刚度的影响.为了更好地说明取向角对仿生复合材料力学性能的影响,绘制不同取向角仿生复合材料的米赛斯应力云图,见图4,在相同米塞斯应力标尺下,材料的取向角越小,仿生复合材料内的应力越小,表明结构的刚度越好.
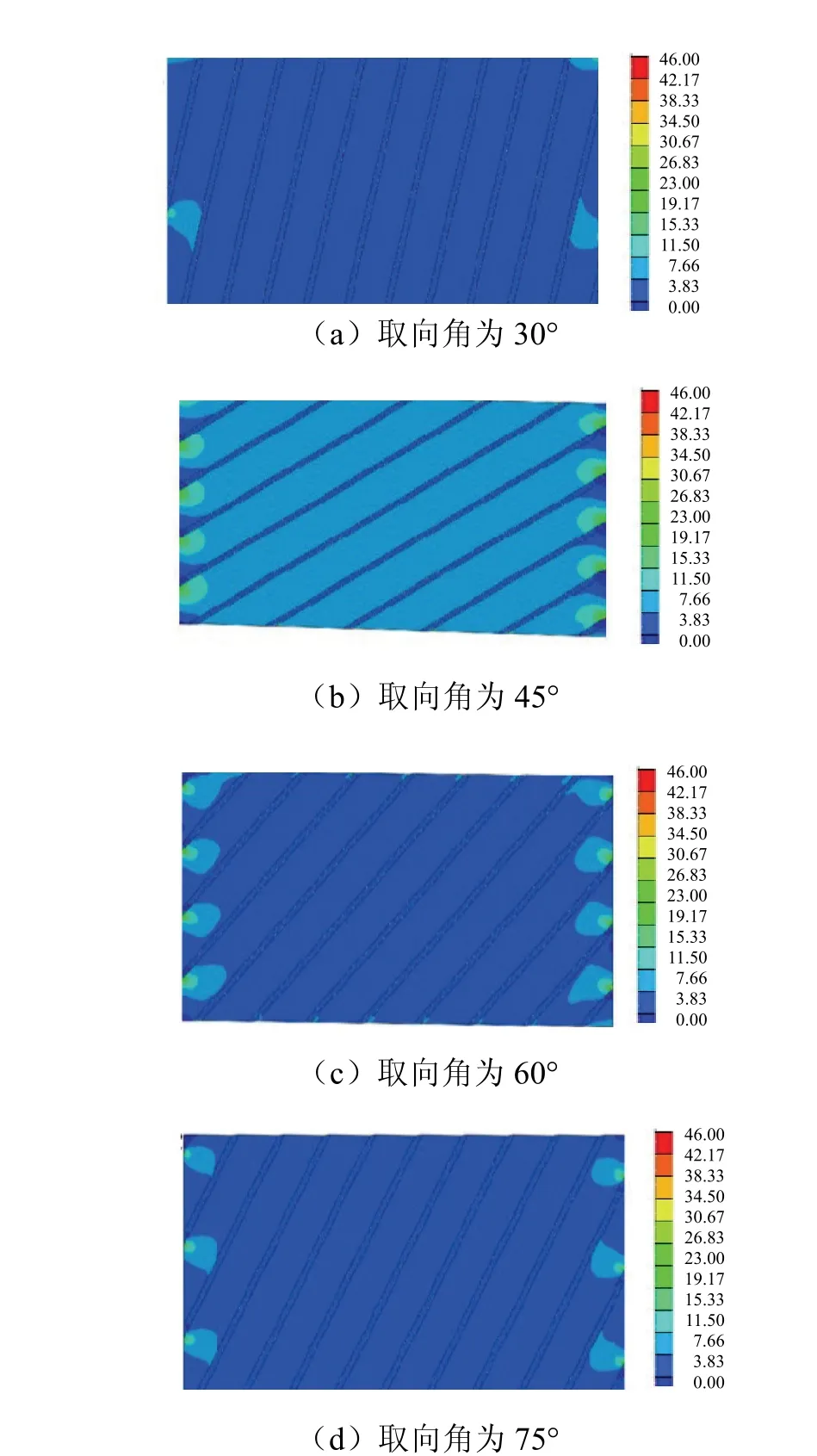
图4 不同取向角仿生复合材料的米赛斯应力 (单位:MPa)Fig.4 mises stress of bio composites with different orientation angles (unit:MPa)
生成相同应力标尺下米赛斯应力云图对单个模型的应力分布,见图5.从图5中可以看到在左右边界处应力分布不均匀程度增加,随着取向角的增大,不均匀性较强,这与结构软相出现尖角有关.当取向角为30o时,软相内的应力小于硬相,通过软相的调节增加了材料的整体韧性.
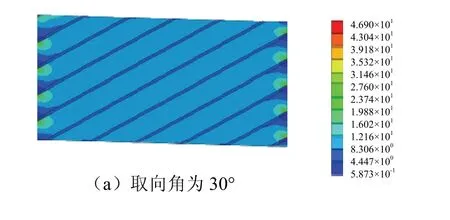
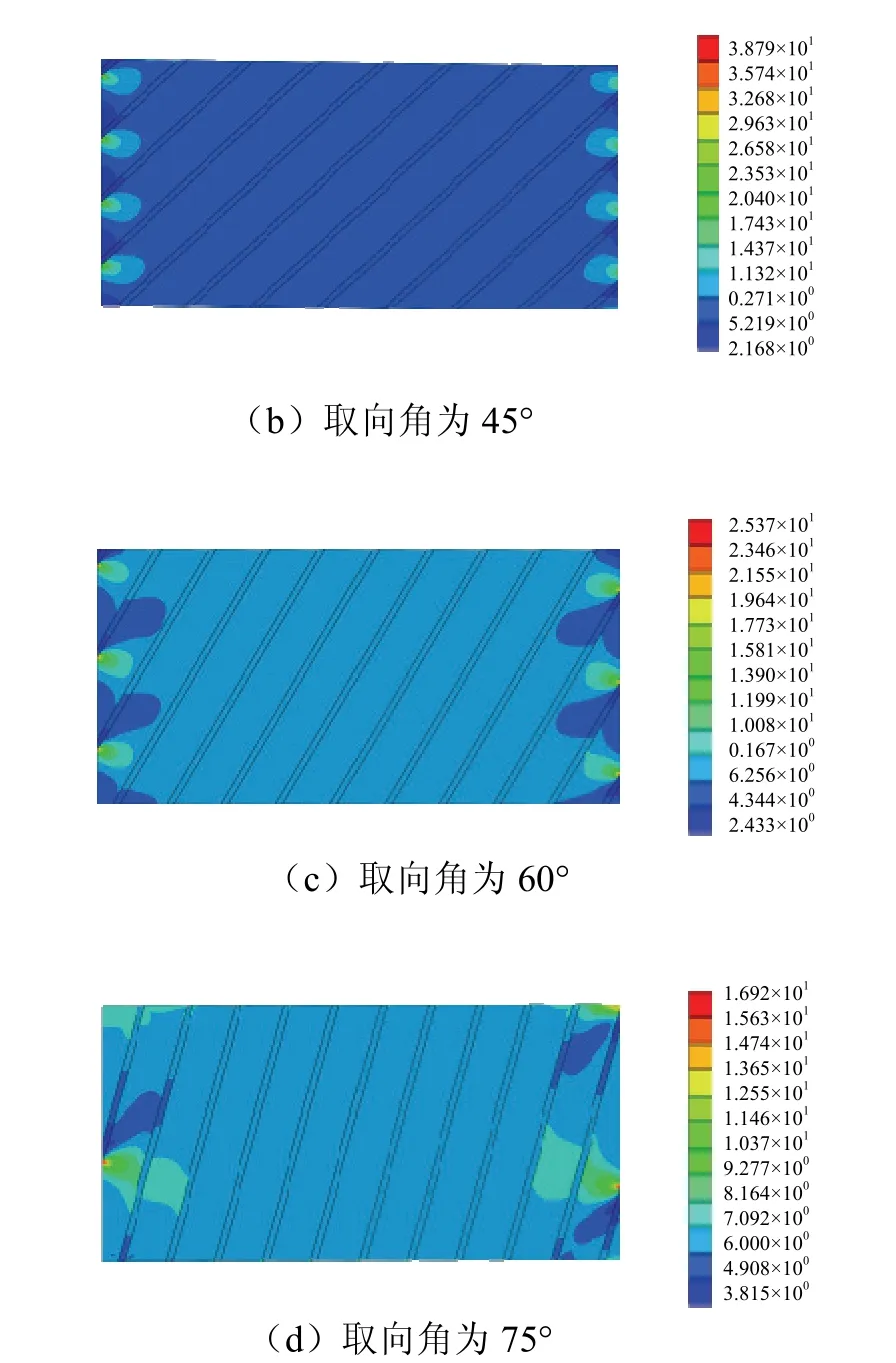
图5 局部标尺下不同取向角仿生复合材料的 米赛斯应力(单位:MPa)Fig. 5 mises stress of bio composites with different orientation angles under local scale (unit:MPa)
4 结论
利用Abaqus软件建立两相仿生复合材料微观模型,计算不同角度下仿生复合材料的弹性模量,绘制弹性模量曲线,得出弹性模量与应力、应变和取向角关系.
(1)弹性模量随着仿生复合材料取向角的增加而减小.
(2)在相同体积分数和相同材料参数下,仿生复合材料的弹性模量逐渐减小,材料刚度降低.
