码垛机器人底座轴承应力特性分析

李小姣，田军亮，李玉龙，段 朋

（1.兰考三农职业学院，河南 开封 475300；2.郑州科技学院，河南 郑州 450052）

0 前言

滚动轴承作为码垛机器人的重要组成部分，在工作中起着支撑和导向作用。滚动轴承的寿命和承载能力是决定码垛机器人主要技术性能指标的关键因素之一。传统滚动轴承的承载能力和疲劳寿命主要采用经验公式和分析方法来计算轴向力和径向力，并通过有限元分析和计算方法得出滚动轴承应力变化规律，然后将应力用于滚动轴承的疲劳分析和评估。本研究利用Adams软件[1]中的动力学分析计算模块，在码垛机器人正常工作的情况下完成动力学分析计算，得到滚动轴承运行时的动态载荷变化，并对其进行仿真，采用有限元分析计算方法得到接触应力的变化规律，并以此作为滚动轴承疲劳寿命分析和评估的依据。

1 码垛机器人动力学分析及仿真

Inventor的应用简化了复杂三维模型的创建，有利于将更多的精力集中在设计功能的实现上[2]。本研究利用Inventor的建模功能，建立了码垛机器人的三维模型数字样机，并通过数据文件将码垛机器人模型导入Adams软件进行动力学仿真。码垛机器人三维模型如图1所示。

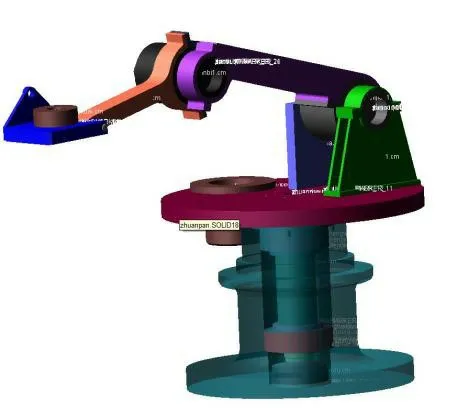
图1 码垛机器人在Adams软件中的仿真模型

为了能够准确地进行码垛机器人的动力学仿真，需要进行如下操作。首先，码垛机器人的每个部分都应该有材料属性，机器人的底座采用铸铁，手臂采用铝合金材料，轴承采用轴承钢。其次，必须将约束添加到每个连接部件，以便码垛机器人进行仿真，因此，除了基座和地面被固定约束外，其他旋转关节和轴承被添加为旋转铰链约束。最后，根据机器人的轨迹和初始条件为每个关节添加正确的驱动关节，以便在调整合适的视角和仿真时间的情况下进行动力学仿真基础轴承的受力分析[3]。

根据码垛机器人的动力学分析计算结果，在Adams后置处理器中对动力学分析结果进行校核，并对码垛机器人进行动力学分析，得到轴承内圈与轴之间铰链接触力沿三个方向的变化曲线[4]。三个方向的变化曲线图分别如图2、图3和图4所示。

图2 X向轴力图

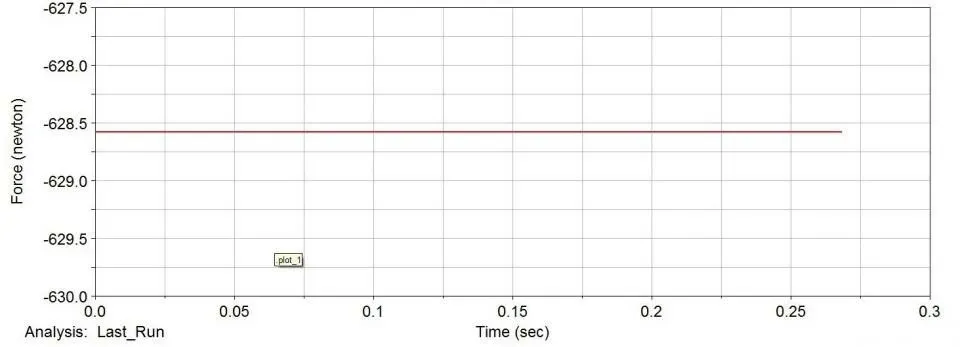
图3 Y向轴力图

图4 Z向轴力图

通过Adams后置处理器的曲线编辑功能，准确地获得了滚动轴承质心的最大力。即Fx=7 891.26 N；Fy=628.5 N；Fz=7 924.96 N，Fx为径向力，Fz为轴向力。因此，轴向力和径向力的最大值分别为Ft=628.5 N和Fr=11 183 N。然后用3D绘图软件测量轴承内表面和上表面的面积，Sinner=13 483.72 mm2，Sup=7 389.03 mm2。通过压力公式P=F/S，得出轴承内表面的压力为Pinner=0.829 MPa，轴承上表面的压力为sup=0.085 MPa。

2 滚动轴承的有限元分析

2.1 滚动轴承的材料特性与啮合

由于滚动轴承属于完全对称模型，因此只需对滚动轴承的1/4模型进行分析和计算。内圈、外圈和滚动体均采用轴承钢GCr15SiMn，密度为7 820 kg/m3，弹性模量为2.16×105MPa，泊松比为0.3，抗压强度为1 813 MPa，屈服强度为1 323 MPa。有限元分析软件Abaqus[5]选择了属于8节点六面体线性非协调有限元的单元C3D8I作为计算单元，因为它具有许多优点。例如，非协调模式可以克服线性完全积分单元中的剪切锁定问题，因此，在单元变形较小的情况下，位移和应力的计算结果更准确。然后利用Abaqus软件中的扫描网格划分技术对滚动轴承的结构网格进行划分，得到69 512单元网格，图5为三维网格模型，图6为接触对的定义图。

图5 三维网格模型

图6 接触对的定义

2.2 定义约束和载荷

码垛机器人滚动轴承正常工作时，外圈固定在机架上，内圈随主轴转动。因此，在滚动轴承外圈上应定义一个固定约束。滚动轴承的分析计算采用1/4实体模型，因此对平面XOY和YOZ施加对称约束。此外，通过码垛机器人动力学分析得到的滚动轴承动载荷必须施加在滚动轴承的相应位置上，因此，滚动轴承的约束和载荷结果如图7和表1所示。

图7 定义了约束和负载

表1 滚动轴承的约束和载荷结果

2.3 压力结果的分析和总结

Mises应力[6]滚动轴承应力特性的等效云如图8所示，它是在Abaqus中完成滚动轴承的网格生成、约束定义和施加载荷后，通过滚动轴承有限元模型的数值迭代计算得到的。

图8 滚动轴承应力特性的Mises应力等效云

首先，外圈的Mises应力[7]云，如图8（a）所示。其显示最大Mises应力为60.52 MPa，出现在滚动体表面与外圈接触区域的顶部，然后Mises应力沿内圈轴线（X）逐渐减小；外接触区的径向最大应力均出现在接触面上。

其次，滚动体的Mises应力云如图8（b）所示，其表明轴向应力主要集中在滚动体与内外环接触面的顶部和底部，中间应力相对较小；此外，滚动体的轧辊径向应力主要出现在接触面上，最大值为224.9 MPa。

再次，内圈的Mises应力云如图8（c）所示。该图显示最大Mises应力为140.2 MPa，出现在内圈内表面的底部，然后Mises应力沿轴（X）逐渐减小；应力主要出现在内圈的底部。

总体而言，滚动轴承的Mises应力云如图8（d）所示。其最大等效Mises应力出现在内部和滚动体之间接触区域的底部，为224.9 MPa，应力主要出现在滚动体与外圈和内圈之间的接触面上[8-9]。这些现象表明，滚动轴承的疲劳损伤主要在接触面上形成。在接触面上出现小的疲劳裂纹，然后逐渐形成疲劳点蚀和冲蚀，最终缩短轴承的使用寿命。

3 结论

本研究以码垛机器人的典型轨迹和给定的载荷条件为基础，利用Adams软件的动力学分析计算模块，在码垛机器人正常工作的情况下进行了动力学分析计算，得到滚动轴承运行时的动载荷变化，进而得出码垛机器人的动力学特性。通过有限元分析[8-9]计算方法得出了接触应力的变化规律，并以此作为滚动轴承疲劳寿命分析和评估的基础[10-11]。从分析计算结果来看，滚动轴承在外载荷和动载荷共同作用下的接触应力分布与常用滚动轴承应力疲劳破坏现象相似，该方法能有效克服传统滚动轴承疲劳寿命计算方法只考虑静态载荷的不足。