一种双余度机电伺服系统设计仿真与优化
2022-08-25张益齐张国林朱阳贞魏泽宇
牛 涛,张益齐,张国林,朱阳贞,魏泽宇
(1. 北京精密机电控制设备研究所,北京,100076;2. 航天伺服驱动与传动技术实验室,北京,100076)
0 引 言
近年来,机电伺服系统因其绿色环保、质量较轻、运营及维护成本较低的优点得到广泛的研究和应用,美国及欧洲均资助了大量机电作动技术科研课题,某些飞行器的辅助飞行操舵系统上部分采用了机电伺服系统。波音公司也在积极探讨机电作动器应用于新一代飞行器的优势和可行性。机电作动器一般由永磁同步电机、滚珠丝杠副等组成,如果要代替液压作动器,安全性和可靠性是主要解决的问题。众所周知,丝杠的卡死故障为机电作动器的致命性故障,有些事故的发生就是因为机电作动器无法容错而导致的飞行控制失效。吴昊等提出在伺服机构在一度故障时,通过隔离故障通道可以提高伺服机构的可靠性。所以,故障容错和余度技术是机电作动器发展的重要方向。
罗战强等完成了双余度稀土永磁无刷电机伺服系统转矩均衡性研究,解决了双余度电机电磁转矩纷争的现象,但其研究内容不涉及丝杠等传动部件;Rottach 等对一种容错的作动系统进行优化设计,但其研究内容只考虑电机容错的内容;和阳等主要研究了高可靠双冗余电动舵机控制器;马瑞卿等致力于研发基于双余度直流无刷电机的双余度舵机,但涉及的电动舵机传动部件还是单点工作模式;付永领等提出的应用于驱动转鳍机构的推挽式机电作动器,是两台作动器同时工作,但不能解决传动机构卡死后的容错问题。
本文提出了一种双余度机电伺服系统,该系统具有余度功能,可以保证传动机构、伺服电机以及控制驱动器出现故障时依然能正常工作。此外,通过建立系统的MATLAB/Simulink 仿真模型,对系统的性能进行仿真分析,验证了该系统结构和控制方法的可行性。
基于以上研究成果,本文对双余度直线式机电伺服系统的机电作动器结构进行优化,减小两路传动环节多个零件的惯量,增加传力结构的刚度,并优化相关控制参数,通过对优化后的伺服系统进行仿真分析,验证优化方法的有效性,从而得到动态性能更优的双余度机电伺服系统方案。
1 双余度机电伺服系统
双余度机电伺服系统主要由双余度机电作动器和控制驱动器组成,如图1 所示,针对高可靠机电作动领域的应用需求,机电作动器采用永磁同步电机,LVDT 传感器测量丝杠的线位移并反馈给控制器,可以使作动器精确定位;控制驱动器在软硬件设计上采用备份和多通道形式,具备故障容错能力,通过交叉反馈技术和在线余度管理策略的复合控制结构,进一步提高系统在故障情况下的瞬态响应特性和容错性。

图1 一种双余度机电伺服系统Fig.1 A Jam-tolerant Electromechanical System
1.1 机电伺服系统的组成
双余度机电作动器具有高比功率、紧凑型的特点,如图2 所示,包括双电机、嵌套式丝杠副和滚珠花键等结构,有主工作模式和备份工作模式两种传动模式,当主工作模式发生故障时,可以切换到备份工作模式,从而保证机电作动器的正常工作。嵌套式丝杠副是双余度机电作动器的重要传动部件,主要由内丝杠和外丝杠装配组成,外丝杠在主工作模式工作,内丝杠在备份工作模式工作;外丝杠在主工作过程任何位置卡死时,内丝杠能够完成行程补偿并实现直线输出,从而使作动器能正常工作。
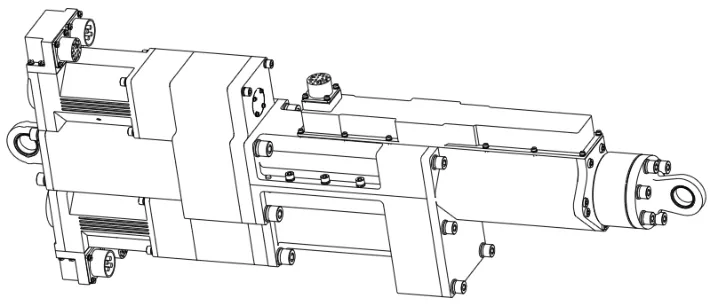
图2 双余度机电作动器模型Fig.2 Double Redundancy Electromechanical Actuator Model
1.2 机电伺服系统的工作原理
a)主工作模式:电控信号指令下,制动器断电制动,将电机2 输出轴抱死,滚珠花键齿轮处于锁止状态,内丝杠锁止,电机1 带动减速器运转,驱动外丝杠工作,将旋转运动转化为直线运动,内丝杠和滚珠花键-齿轮副随外丝杠丝杆做直线运动,输出直线位移。
b)备份工作模式,在主工作环节发生故障时,如外丝杠卡塞等,备份工作模式启动,备份工作模式的工作原理是:在电控信号指令下,制动器将电机1 输出轴锁止,外丝杠锁止,电机2 解锁,驱动减速器运转,并通过传动齿轮,带动滚珠花键-齿轮副运转,驱动内丝杠工作,从而输出旋转直线位移,并在输出端支耳的作用下,消除旋转运动,输出直线运动。
2 建模与参数计算
2.1 建 模
a)永磁同步电机。
采用永磁同步电机,选用MATLAB 库中的电机模型,根据永磁同步电机(PMSM)的等效电路方程、电磁转矩方程等建立PMSM 模型。
b)减速器。
行星减速器的传动关系等效为以下模型:
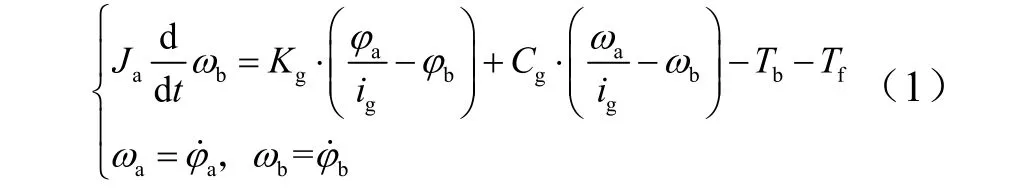
式中为摩擦力矩;为输入转矩;,分别为输入和输出转角;,分别为输入和输出转速;为减速器的减速比;,分别为阻尼和扭转刚度;为转动惯量。
c)其它传动部件。
滚珠丝杠副等传动部件整体模型(除减速器),输入转矩的与输出线性位移的公式为
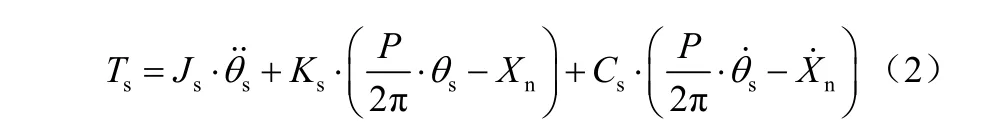
式中,分别为扭转阻尼和扭转刚度;为输出位移;为丝杠的导程。
d)舵面模型。
根据伺服系统的实际工作情况建模,机电作动器推动舵面绕转轴摆动,建立舵面模型的动力学方程为
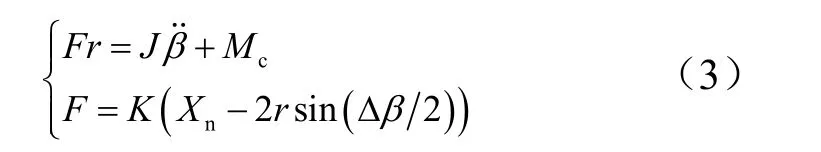
式中为摇臂长度;为机电作动器推力;为综合刚度;为摇臂与舵面的初始角度;为舵轴转动惯量;为摩擦转矩。
e)控制器模型。
伺服闭环控制算法采用PID 控制,算法见图3。
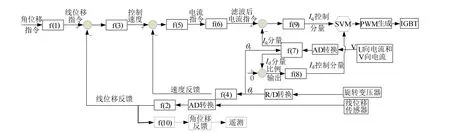
图3 伺服控制框图Fig.3 Servo Control Method
f)间隙影响。
滚珠丝杠副因为施加了预紧力矩,消除了间隙,轴系之间的平键连接为过盈装配,传动无间隙,所以,在建模时只考虑行星减速器的间隙。
行星减速器模型引入死区模型作为间隙模型的表述,表达式如下所示:
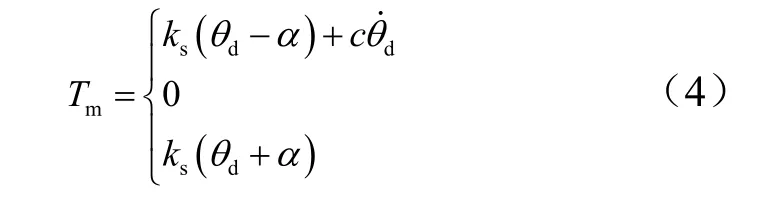
式中为减速器输入轴的力矩;为减速器的扭转刚度;为输入端与输出端经过折算后的相对转角;为单边间隙;为阻尼。
2.2 参数计算
a)惯量计算。
1)主工作模式下各传动环节惯量计算。
电机2 被制动器抱死,电机1 在指令输入后工作,带动减速器工作,并将运动通过外丝杠传递到作动器支耳,输出直线运动。
该工作模式包含的惯量环节主要有:电机转子、制动器转子、行星减速器组件(太阳轮、行星轮、外齿圈等)、角接触球轴承、主工作齿轮、锁紧螺母、外丝杠螺母以及平动的其它组件(包括嵌套式丝杠其余部分、传感器连接部分、前支耳组件等)。
转动部件的转动惯量可以根据公式得到:

式中为回转体半径;为密度;为体积。
直线运动部件(包括嵌套式丝杠其余部分、前支耳组件等)可以根据以下公式完成惯量折算:

式中为平动部件的质量;为动量。
各传动部件惯量折算到电机轴惯量可得:

式中为电机转子的转动惯量;为传动部件的总惯量;为电机到传动部件的减速比。
2)备份工作模式下各传动环节惯量计算。
电机1 被制动器抱死,电机2 在指令输入后工作,带动减速器工作,并将运动通过传动轴和滚珠花键副传递到内丝杠,内丝杠螺母边旋转边直线运动,最后通过前支耳组件的作用,输出直线运动。
该工作模式包含的惯量环节主要有:电机转子、制动器转子、行星减速器组件、传动轴、传动齿轮、锁紧螺母、滚珠花键螺母、内丝杠螺母以及平动的组件(包括传感器连接部分、前支耳组件等)。
转动部件(制动器转子、传动轴、传动齿轮、锁紧螺母、滚珠花键螺母、内丝杠螺母、减速器等)惯量可以根据式(5)得到,直线运动部件(包括支耳组件等)可以根据式(6)完成等效惯量折算,各传动部件惯量折算到电机轴惯量可以根据式(7)计算。
b)刚度计算。
1)行星减速器扭转刚度。
行星减速器刚度主要包括输入轴刚度、输出轴刚度、太阳轮刚度、行星轮刚度和行星架刚度。
在计算过程中,选取输出轴锁定,对于输入轴和输出轴,扭转刚度用以下公式计算:

式中l为轴受扭矩作用的轴长度;为轴的抗扭截面强度; I为极惯性矩;对于输入输出轴,=1,2。
齿轮的刚度可近似用下面公式计算:

式中为齿宽;为齿厚;为齿轮材料弹性模量;为齿轮节圆半径;为齿高。对于3 个齿轮,=3,4,5。
减速器总扭转刚度:

2)滚珠丝杠副刚度。
由于外丝杠与内丝杠的导程、接触角、滚珠直径、螺纹滚道曲率半径相同,故接触刚度与内丝杠的相同。
内丝杠螺母、外丝杠螺母,刚度K计算方法如下:

式中E为弹性模量;为截面积; l为配合长度。
内丝杠丝杆、外丝杠丝杆由连续的变截面结构组成,刚度用公式计算:

式中为弹性模量; A为截面积;l为结构长度。
内丝杠接触副和外丝杠接触副的刚度通过接触理论公式计算得到。
滚珠与丝杠滚道的弹性趋近量:
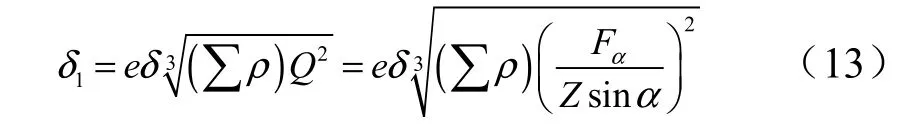
式中为作用滚珠数量;F为作用力;为接触角。
滚珠与螺母滚道的弹性趋近量:
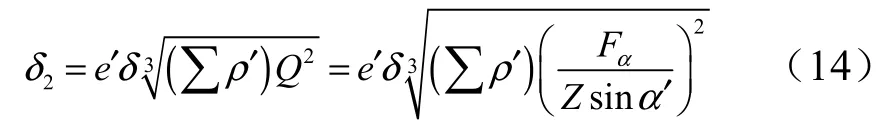
则丝杠滚道与螺母滚道的轴向弹性趋近量为

滚珠丝杠副轴向接触刚度为
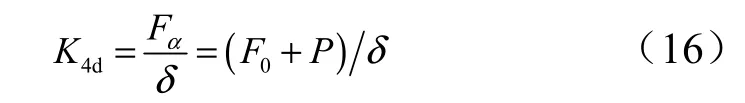
式中为丝杠预紧力;为外加轴向载荷。
刚度环节为串联关系,滚珠丝杠副的总刚度计算:

通过以上的计算,得到伺服系统主工作模式和备份工作模式的惯量和刚度,以此作为仿真模型的参数,进行后续的仿真计算。
3 故障切换控制策略
表1 为各故障模式。在伺服系统工作过程中,若通过表1 中监测方法检测到对应的故障模式,则从主工作模式切换到备份工作模式,从而保证伺服系统继续工作。
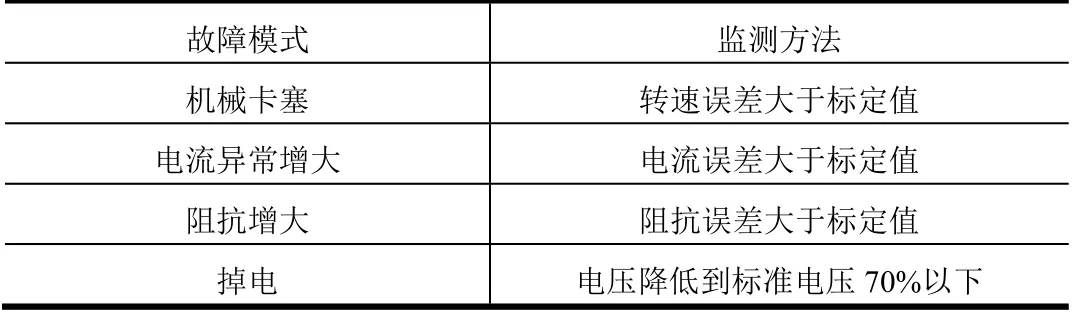
表1 故障模式表Tab.1 Failure Mode
由于主工作模式和备份工作模式的机械传递路线不同,转动惯量、刚度等特性不相同,在遇到故障进行余度切换时,需要针对两种工作模式提出不同的控制策略和控制算法。这两种控制算法分别适应主备工作模式,使得切换以后,机电伺服系统的功能和性能都应满足要求。
4 仿真分析
4.1 模态仿真分析
分别针对两种工作模式,完成两种条件下的仿真分析,从而得到正弦扫频指令信号下,伺服系统的输出和信号之间的关系。
基于控制方法,对不同模式的工作情况进行仿真分析。仿真结果展示了作动器主工作模式下的频率响应曲线(见图4),以及备份工作模式下的频率响应曲线(见图5)。通过频率特性曲线可知,主工作模式下,幅值衰减到-3 dB 时,频率约15 Hz,对应相频约-63°,而在备份模式下幅值衰减到-3 dB 时,频率约14.6 Hz,对应的相频约-66°。两种工作模式下,备份工作模式的动态特性比主模式稍微差一点,但都满足要求。
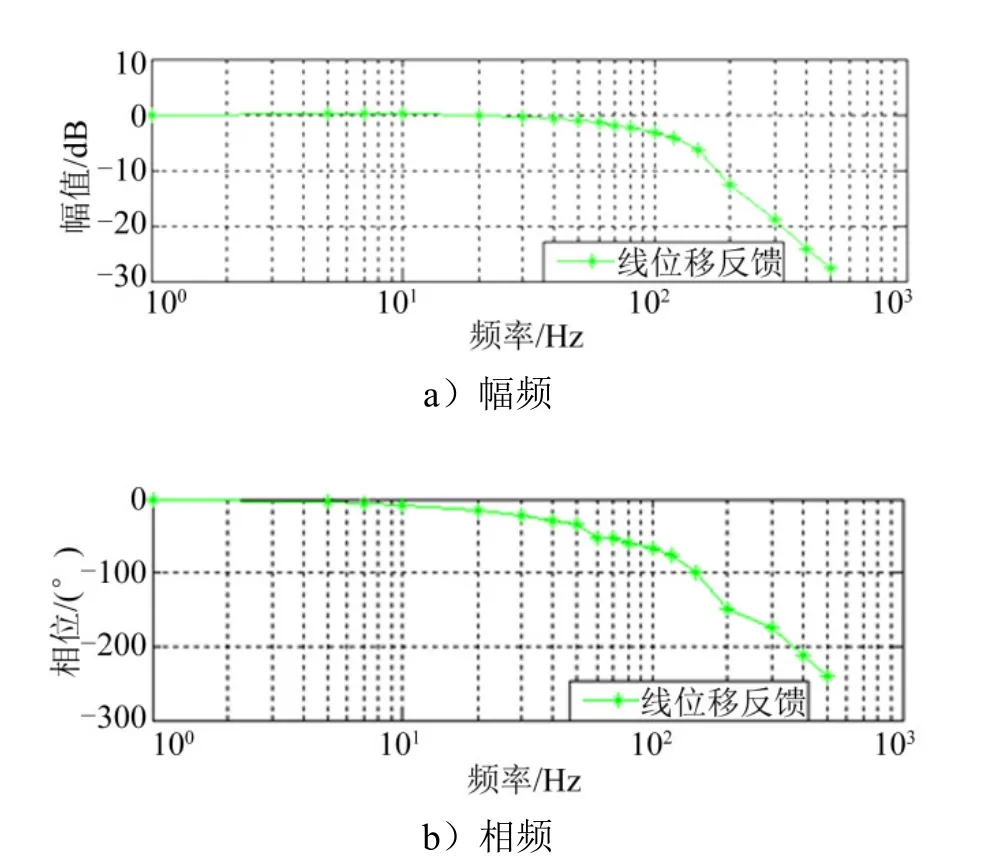
图4 主工作模式的频率特性响应曲线Fig.4 Frequency Response Curve in Main Operating Mode
图5 备份工作模式的频率响应曲线Fig.5 Frequency Response Curve in Backup Mode
4.2 优化设计
通过对主工作模式和备份工作模式的传动齿轮、电机、滚珠丝杠副、滚珠花键等结构进行优化,减小转动部件的转动惯量,同时优化控制参数,以提高两种工作模式下的动态响应能力。
4.3 优化后模型仿真分析
将优化后的物理参数和控制参数输入到仿真模型中,对两种工作模式再分别进行仿真分析,得到主工作模式的仿真结果如图6 所示,备份工作模式的仿真结果如图7 所示。通过频率特性曲线可知,在主工作模式下,相比原动态性能,优化后的模型动态特性指标由15 Hz 提高到18.5 Hz,而在备份工作模式下,优化后的模型动态特性指标由14.6 Hz 提高到17.5 Hz。经过优化结构和控制算法,两种工作模式的动态特性均有提高,主工作模式动态性能提升更多。
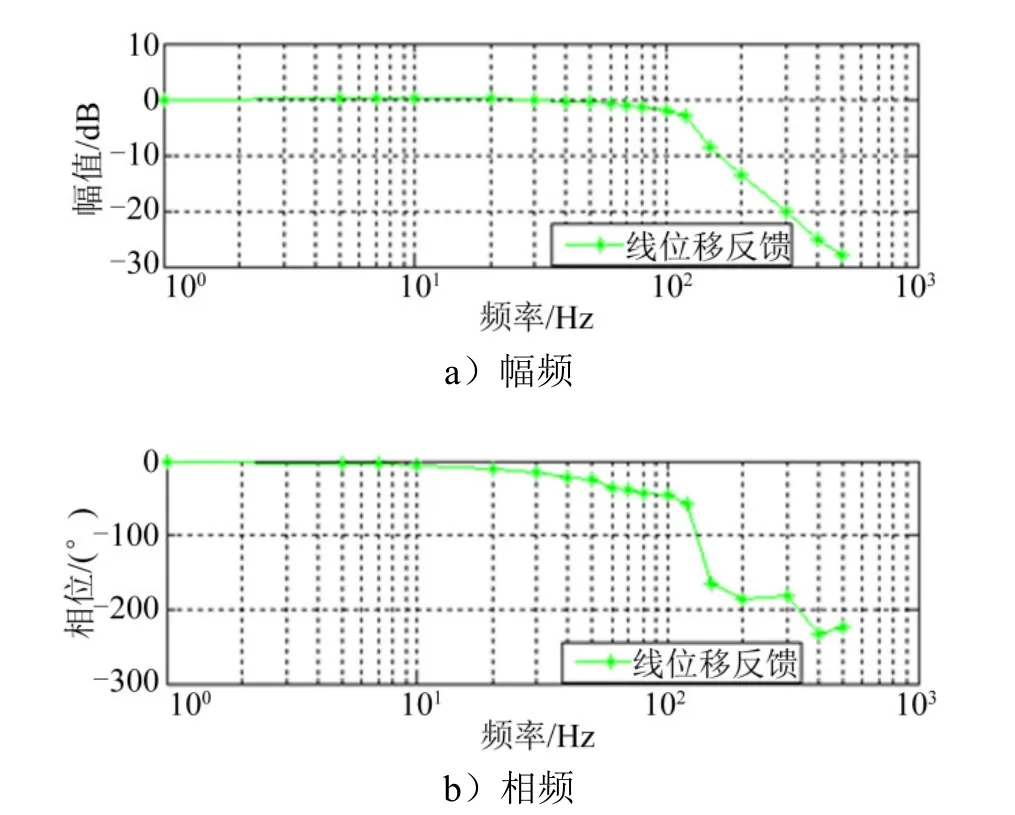
图6 优化后主工作模式仿真结果分析Fig.6 Simulation of the Main Working Mode after Optimization
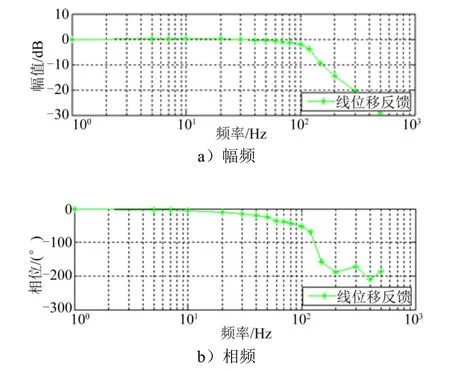
图7 优化后备份工作模式仿真结果分析Fig.7 Simulation of the Main Working Mode after Optimization
5 结束语
本文提出一种双余度机电伺服系统,通过主备两种工作模式实现伺服机构双余度的功能,满足单路故障时系统的正常工作要求。通过建立系统的MATLAB/Simulink 仿真模型,对伺服系统的性能进行仿真分析,并在分析结果的基础上,优化伺服系统的模型和控制算法,从而提高了该系统的动态响应能力。
