再入飞行弹道解析计算方法研究

朱恒伟，肖 振，曹晶莹，杨 丁

（空间物理重点实验室，北京，100076）

0 引 言

从20 世纪50 年代起，科研人员就开始了对于滑翔弹道解析解的研究。在定升阻比的条件下，Chapman给出了再入弹道的近似解析解；在此基础上，Loh放宽约束条件，得到了升阻比变化条件下的再入弹道近似解析解；Vinh 等则给出了定升阻比平衡滑翔纵向弹道解析解；Bell将问题扩展到三维，分析了定升阻比和定倾侧角条件下的平衡滑翔三维弹道解析解。随着预测校正制导技术的发展，研究重点转向了高精度的纵向弹道解析。郭兴玲等提出用包含地球旋转效应的常滑翔角飞行段近似实际滑翔飞行轨迹的方法，并基于该方法推导得到了长航时纵向远程滑翔飞行轨迹近似解；李邦杰等则给出了平衡滑翔最大升阻比条件下的高度、弹道倾角、飞行时间和射程的解析解；徐明亮等在准平衡滑翔条件下，假设速度倾角是常值，得到了航程、高度和速度倾角三者之间的解析关系式；Yu 等通过给定纵向升阻比和横向升阻比关于能量的表达式，推导得到了准平衡滑翔轨迹的纵程、横程和速度倾角的解析解；胡锦川等将弹道分段，并将升力系数分解为横向分量、平衡滑翔纵向分量和平稳滑翔纵向分量3 部分，以此为基础推导得到了滑翔轨迹的解析解。

本文重点针对高速飞行器平衡滑翔阶段的弹道工程估算问题，推导出高速飞行器再入飞行的解析解。以滑翔弹道简化方程为基础，分别采用摄动法求解高度和弹道倾角的数值解，数值积分法求解航程与飞行时间的数值解，同伦分析法求解拟纬度和航向角的数值解，由此得到平衡滑翔阶段弹道的近似解。

1 弹道方程的简化

高速飞行器处于平衡滑翔阶段时，其弹道倾角及其变化率满足如下条件：

在高速再入的初期，飞行高度很高，弹道倾角很小，一般不能满足相容初始条件。如果飞行高度过低，在只能利用向上的升力时也难以满足相容初始条件（虽然可利用负升力维持平衡，但此时飞行器所承受的热载荷很大，不能长时间维持）。对于初始条件不可能相容的情况，都要经过特殊的拉平段飞行，使飞行器达到平衡滑翔的初始状态（称为弹道拉平），然后才能进行平衡滑翔飞行。

2 主要解析解推导

2.1 高度和弹道倾角的解

当忽略式（11）中关于的二次项时，就等于将式（10）右端所含直接变为的结果。

从物候期观测结果分析，各类月季均能正常发芽、开花、结果，在未采取冬季防冻、旱的情况下，除冷香玫瑰外，其余各品种均不能正常越冬，在西宁地区引种栽培均需采取防冻、旱措施。

由式（6）可得：

2.2 航程的解

由式（2）的第2 式、第4 式可得：

其实，内乡县衙大堂上还挂着一副对联：“欺人如欺天毋自欺也，负民即负国何忍负之。”建议当代官员们多念叨几遍这副对联，多照照镜子。没有民，哪有官，你给谁当官？官待民要不“欺”不“负”，要爱要畏，否则，为官者羞见内乡县衙的对联！

3 仿真分析

对滑翔飞行器的剩余航程进行估计，所得结果如图2 所示。

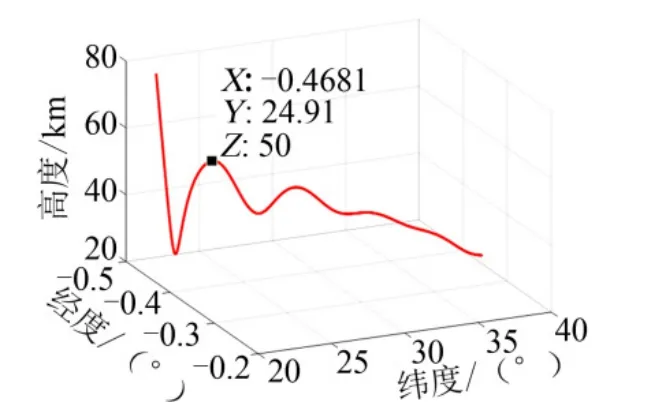
图1 某滑翔飞行器三维弹道（示例1）Fig.1 The Three-dimensional Trajectory of Glide Vehicle(Exampe 1)

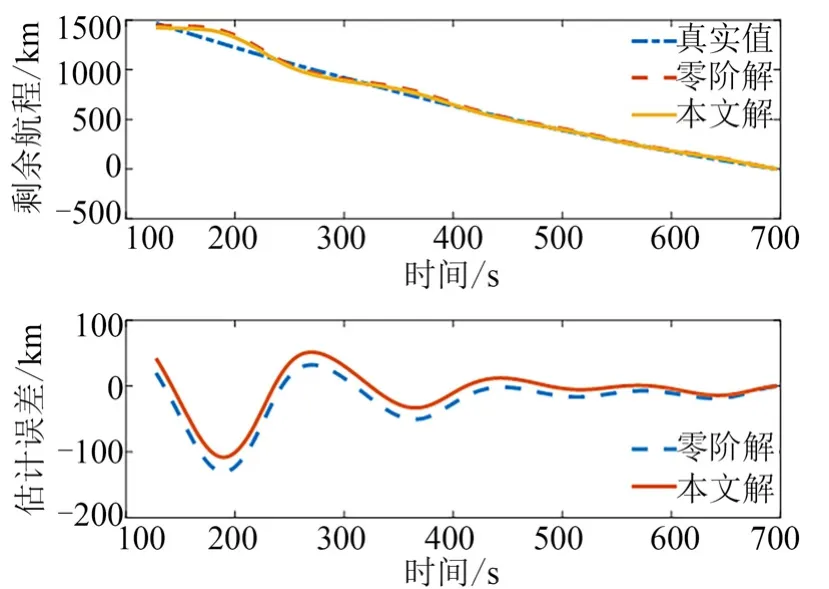
图2 剩余航程估计及估计误差（示例一）Fig.2 The Estimation and Its Error of Remaining Range(Exampe 1)

某滑翔飞行器示例2 的三维弹道如图3 所示，仿真中采用最大升阻比约为3.2 的某型滑翔飞行器的飞行数据，滑翔飞行器终端速度=1800 m/s，分别使用式（20）所示方法和工程中常用的零阶解方法对滑翔飞行器的剩余航程进行估计，所得结果如图4所示。

图3 某滑翔飞行器三维弹道（示例2）Fig.3 The Three-dimensional Trajectory of Glide Vehicle(Exampe 2)

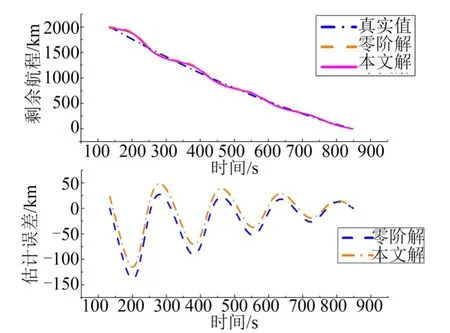
图4 剩余航程估计及估计误差（示例2）Fig.4 The Estimation and Its Error of Remaining Range(Exampe 2)

由仿真结果可看出，本文方法相比零阶解方法估计精度高，能够对零阶解方法估值略高的不足进行补偿，但本文方法求解的过程稍微繁琐，两种方法在具体的工程应用中需根据实际问题的需求进行选择。

4 结束语

滑翔飞行器解析解的研究能够为滑翔飞行特性的理论研究、基于解析解的轨迹生成和制导方法提供基础，本文针对平衡滑翔阶段的剩余航程估计问题进行了近似解的推导，所得结果能够实现对剩余航程更高精度的估计。