空间飞行器离轨段制导策略研究

肖 振，张箭飞，陈 芳，巩英辉，武 斌

（空间物理重点实验室，北京，100076）

0 引 言

随着天地往返技术发展，新型的空间飞行器不断涌现。空间飞行器主要负责将载荷进行定点投放，其运行轨迹按照飞行特点可以分为在轨段、离轨段。其中离轨段通过飞行器携带的轨控发动机制动反推进行减速离轨，减速至满足条件后将载荷投放；高精度离轨制动是确保载荷精准投送的前提，同时在离轨过程中也存在动力、测控等系统方面的各项约束，需通过离轨段制导策略设计进行统筹解决，因此高效可行的离轨制导策略是空间飞行器离轨制动的关键。

目前，对于需要按时返回的空间飞行器，例如神舟飞船、航天飞机、返回式卫星等，离轨均必须采用主动离轨方式，即经过制动前调姿、制动、过渡段惯性飞行3 个阶段，以精确到达再入点，并实施后续进入大气层的再入飞行。

基于空间定点投放任务，对离轨段总体设计条件进行分析，对离轨段设计约束进行梳理，针对设计约束开展制导策略研究，提出解决方案，通过仿真分析对制导策略设计的工程可实现性进行评估。

1 离轨制导总体设计条件分析

1.1 弹道剖面

在进入离轨段后，通过飞行器上携带的反推轨控发动机进行制动减速，降低轨道能量进而使轨道高度逐渐下降，满足离轨条件后，飞行器与载荷分离，完成定点投送任务。

1.2 制导设计条件分析

离轨段制导总体方案设计内容以及涉及到的总体参数如表1 所示。

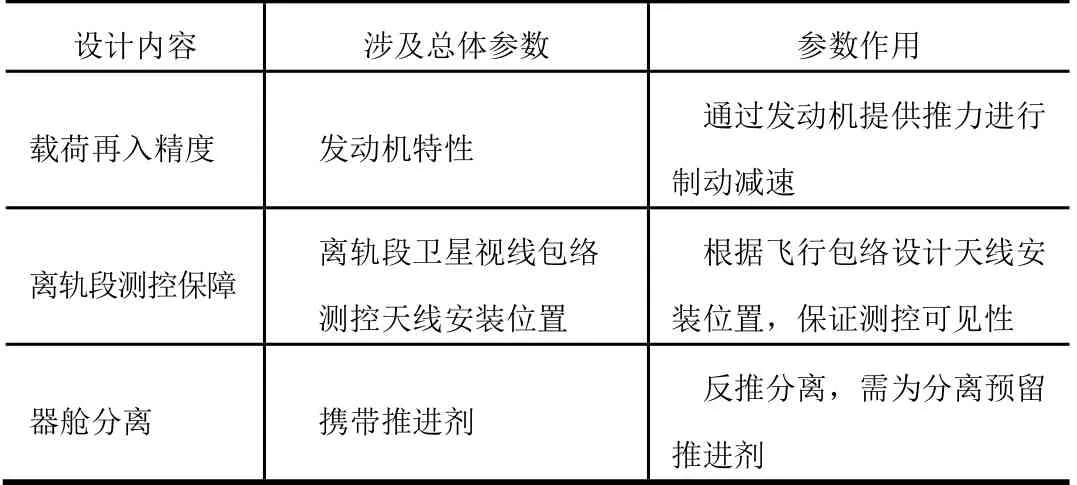
表1 制导设计条件Tab.1 Guidance Design Conditions

2 制导约束条件分析

2.1 定点投送精度约束

经过制动离轨后，飞行器与载荷分离，离轨分离时刻飞行航程精度直接决定载荷再入飞行距离，进而决定载荷飞行的力热剖面。选择合适的离轨制动策略，提高飞行器投送精度，可降低载荷再入过程中力热环境，确保其后续飞行安全。

2.2 推进剂约束

在总体质量确定的情况下，空间飞行器可携带推进剂量受运载能力的制约，离轨段的制动力除了要满足减速需求外，还需要为制动过程中控制飞行高度、弹道倾角提供控制力，同时在轨控发动机存在天地一致性差异的情况下，还需要考虑有限推力作用弧段的引力损失问题，需结合推进剂约束和灵活离轨策略来实现离轨再入的可靠性。

为减少携带载荷，空间飞行器采用反推分离设计方案，利用轨控发动机提供的制动力取代分离弹簧，满足分离条件后，在轨控发动机不关机的情况下进行分离装置解锁，利用轨控发动机产生的制动力，建立起飞行器与载荷的速度差实施分离。受运载器运载能力限制，飞行器自身携带推进剂有限，既要保证飞行器与轨控舱分离时尽量减速至满足再入条件，又要避免分离前轨控发动机推进剂耗尽，影响最终分离。

2.3 天基测控约束

天基测控是确保离轨制动任务可靠、安全实施的必要条件。离轨制动前后需完成制动前调姿、制动减速、分离前调姿、分离触发等关键时序，同时在离轨制动过程中，要监视飞行器位置、速度、姿态、发动机工作状态等遥测参数。天基测控对飞行器具有姿态需求，当天基测控的姿态需求与离轨制动的姿态需求产生矛盾时，应优先满足离轨制动需求，同时离轨制动需充分考虑测控条件的约束，最大化使用测控支持。

3 制导策略设计

针对上述任务剖面分析、设计条件分析以及设计约束分析，开展制导策略设计，针对再入点精度约束，设计了基于推力辨识的制动开机判据；针对推进剂约束与分离可靠性约束，采用视速度增量对剩余推进剂进行预示；针对天基测控约束，在不改变制动推力方向的前提下，通过选择中继星、优化天线安装角度来满足测控对星需求。

3.1 基于推力辨识的制动开机策略

轨控发动机推力偏差是造成离轨航程偏差的主要因素，为了提高航程精度，需在离轨段前获取轨控发动机实际制动加速度，在制动离轨前开启轨控发动机进行推力辨识，根据导航加速度计的输出计算实际推力加速度为

3.2 基于视速度增量的分离判据设计

为防止分离前推进剂耗尽，以离轨段轨控发动机开机为起点，采用视速度增量计算方法对轨控发动机消耗推进剂进行预示，每个导航周期内的视速度增量进行累加：

3.3 基于仿真的测控天线安装需求分析

a）确定飞行器所在位置。

在地球固连坐标系（原点为地心，轴指向格林尼治子午线，轴垂直于地球赤道面指向北极，轴由右手定则确定）对飞行器位置进行计算，已知飞行器经度、纬度、高度（，，）信息，转换至地固系位置：

b）进行覆盖性分析，筛选可见中继星。

由于地球曲率的影响，中继卫星对空间的覆盖区域受到限制，如图1 所示。根据中继卫星对地表的最大覆盖范围计算方法，单颗中继卫星覆盖的最大地球区域对应的半地心角为

图1 单颗导航卫星对地覆盖区域Fig.1 Ground Coverage Area

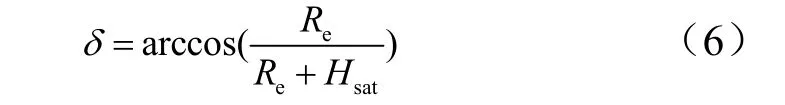
式中为地球轨道平均半径；为中继卫星高度。

中继卫星为地球同步卫星，轨道高度为36 000 km，地球平均半径为6371 km，代入式（6）计算得到中继卫星覆盖的半地心角约为81°。

式中为飞行器位置在地球固连坐标系下的表示。

当小于中继卫星覆盖半地心角时，认为中继卫星对飞行器是可见的，根据离轨段沿飞行轨迹计算结果选取可见的中继卫星。

c）根据仿真包络，计算天线安装角。

已知地固系下飞行器俯仰、偏航、滚转角为、、，建立地固系到弹体系转换矩阵如式（8）所示。

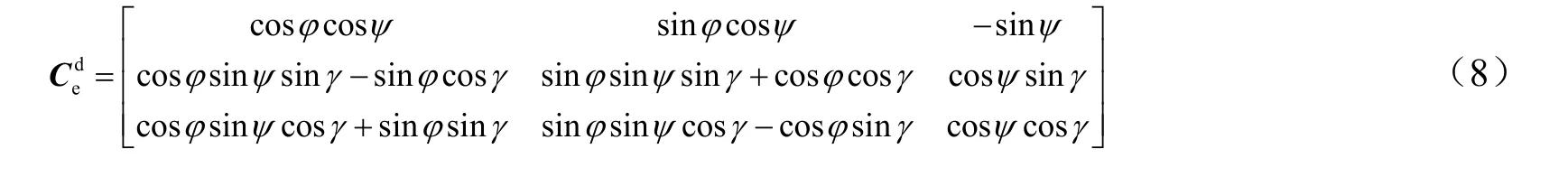
中继卫星在弹体坐标系下的位置矢量如式（9）所示。

矢量在弹体系的视线俯仰角、偏航角分别为

弹体系的视线俯仰、偏航角定义见图2，根据中继卫星及偏差组合下的飞行包络，计算视线角包络，以此为参考开展天线安装角设计，为测控方案提供支撑。

图2 弹体系下视线角定义Fig.2 Sight Angle Definition in Projectile System

4 仿真计算与分析

a）仿真参数。

离轨初始点轨道根数如表2 所示，中继卫星轨道根数如表3 所示。

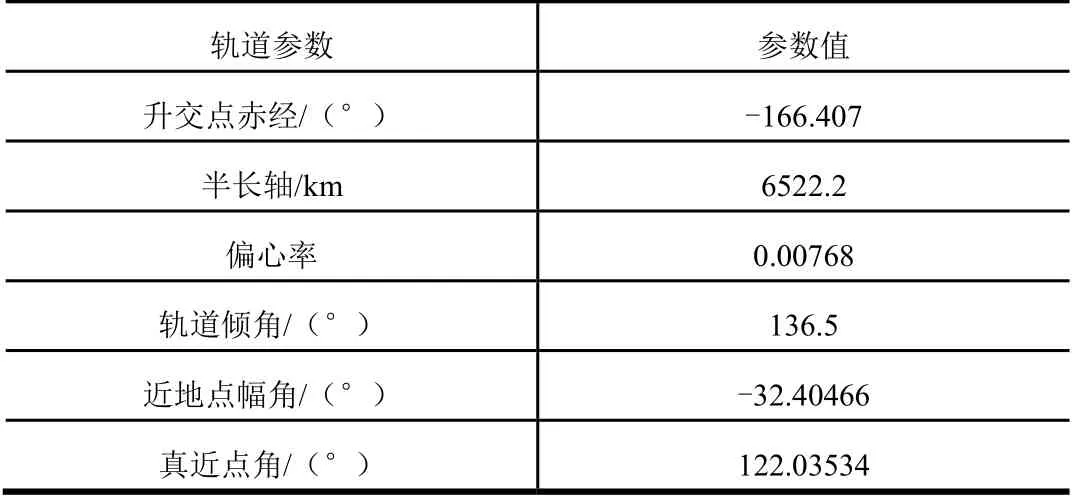
表2 离轨初始点轨道根数Tab.2 Track Parameters of Initial Departure Point

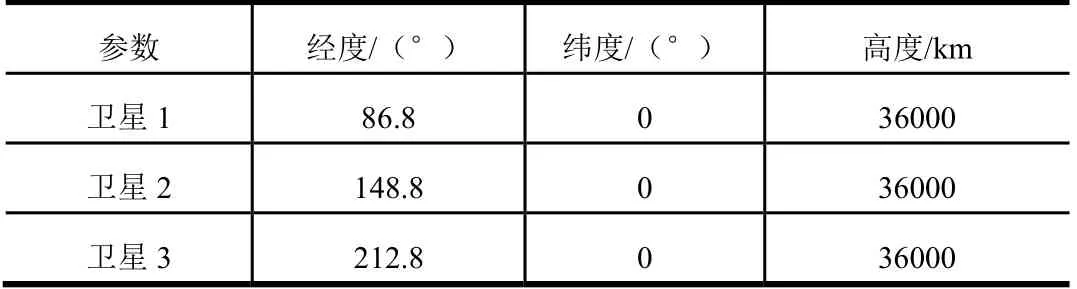
表3 中继卫星轨道根数Tab.3 Track Parameters of Relay Satellite

b）推力辨识制动开机策略仿真分析。

仿真工况中加入+10%的发动机推力偏差，对比有无推力辨识策略情况下的离轨段仿真见图3，3 种工况下的仿真具体指标见表4。通过仿真结果可以看出，在发动机推力偏差+10%的情况下，通过推理辨识策略修正制动起始时间，可以将航程偏差从216.8 km 缩小至69 km，大幅度提高再入点航程精度。

图3 各工况下的离轨段飞行距离Fig.3 Flight Distance of Deorbit Trajectory

表4 离轨段飞行距离Tab.4 Flight Distance of Deorbit Trajectory

c）视速度增量判据设计。

通过大规模仿真对Δ进行设计，在不考虑推进剂消耗上限并采取速度关机的情况下，通过大规模仿真得到视速度增量与推进剂消耗的对应关系见图4。

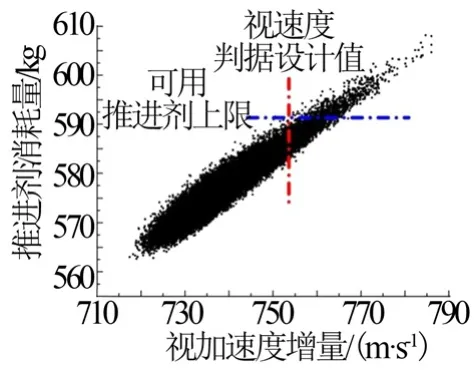
图4 视速度增量与推进剂消耗之间关系Fig.4 Relationship between Acceleration Increment and Propellant Consumption

根据总体方案，在排除用于反推分离、姿态控制所需的推进剂后，留给轨控发动机的可用推进剂最大值为592 kg。根据仿真结果可以看出，选择轨控消耗到达592 kg 对应的最小视速度增量754.195 m/s，根据式（4）计算后，将视速度增量判据Δ设计为752.324 8 m/s，仿真统计中可以看出，将Δ设计为该指标时，打靶仿真情况下约3.5%的偏差组合状态将会触发视速度增量判据引发器舱分离，飞行器的最大再入速度偏差约为33 m/s。

d）测控覆盖性仿真分析

根据中继卫星位置，沿离轨段弹道首先进行卫星覆盖性分析，仿真结果见图5，可看出离轨段飞行器与2 号中继卫星的地心矢径夹角小于中继星覆盖半地心角，与1 号中继卫星和3 号中继卫星的地心矢径夹角大于中继星覆盖半地心角，因此在离轨段飞行器与2 号中继卫星相互可见，与1 号、3 号中继卫星不可见。

图5 离轨段卫星覆盖性分析Fig.5 Satellite Coverage Analysis of Deorbit Trajectory

进行离轨段偏差组合仿真，得到偏差组合下的2 号中继卫星在弹体系下的视线角包络如图6 所示，可据此设计测控天线的安装角度以及天线波束角范围。

图6 弹体系下视线俯仰角、偏航角仿真包络Fig.6 Simulation Envelope of Sight Angle in Projectile System

5 结束语

基于空间定点投放任务，对离轨段总体设计条件进行分析，对离轨段设计约束进行梳理，针对约束条件进行制导策略研究，通过仿真分析验证了制导策略的正确性与工程可实现性，提高了空间定点投放精度，优化了离轨过程中推进剂使用效率，提升了离轨过程中天基测控的可靠性，为未来空间飞行器定点投送任务制导总体设计提供了支撑。