基于PBL教学模式的数学关键能力——建模能力培养的策略研究

北京市第十五中学 郑毅斌

《普通高中数学课程标准（2017年版2020年修订）》中提到，数学学科核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，是在数学学习和应用过程中逐步形成和发展的。高中数学确定了数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析六大核心素养。从数学学科核心素养的定义来看，数学关键能力是数学学科核心素养的必备成分，不可或缺，数学关键能力确保数学学科核心素养在内涵上实现了知识与能力的统一。

新课标指出要培养学生会用数学的眼光观察世界，会用数学思维思考世界，会用数学语言表达世界（以下简称“三会”）。“三会”既在一定程度上诠释了数学学科核心素养，也体现了学生从数学视角提出问题、分析问题、解决问题的能力。构建高中生数学关键能力操作性定义的基本结构，如图1所示，以数学观察、数学思考、数学表达作为一级维度。其中，数学观察维度包括数学抽象能力、直观想象与化归能力；数学思考维度包括数学猜想与论证能力、数学运算能力；数学表达维度包括数据分析与预测能力、数学建模能力。数学建模能力是一个不容小觑的数学关键能力。

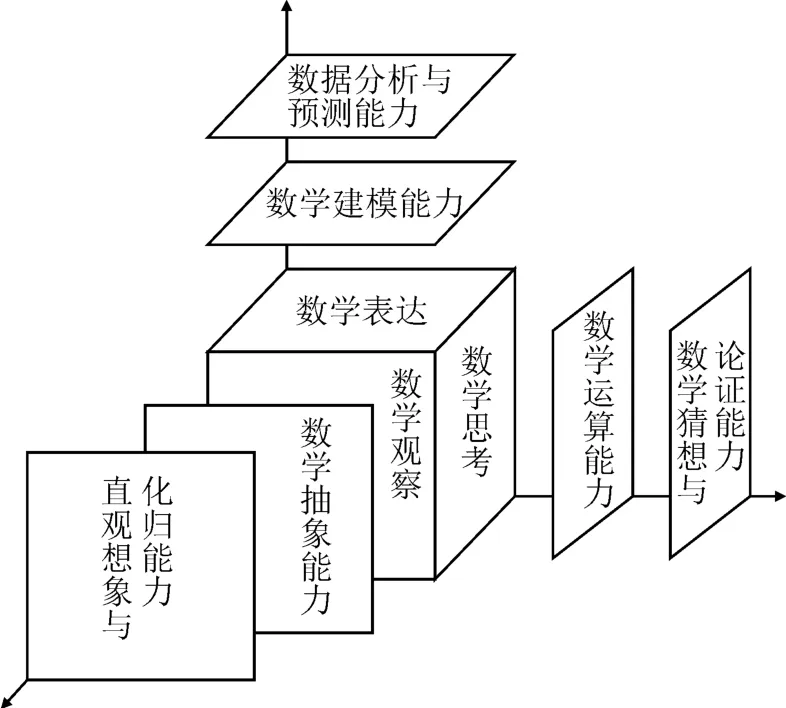
图1 构建高中生数学关键能力操作性定义的基本结构

一、PBL教学模式

PBL教学模式（problem－basedlearning），主要是以问题为导向的教学方法，体现了以学生为中心的教育理念，PBL教学模式是在传统教学的基础上，结合高中生认知规律与思维特征，以自主、合作理念为核心的新型教学方法，是一种以问题为中心的教学模式。教师通过设置合理的教学情境，鼓励学生自主探究、勇于提问，且通过分析、讨论与实践获得知识结构、应用技能的提升，以促进个体的全面综合发展。PBL教学模式有着很强的应用指向，学生通过独立思考、自主学习、合作交流，分析问题直至解决问题，挖掘问题中蕴含的数学思想和隐含的知识内涵，从而形成正确的数学思想方法，提高问题解决能力和自主学习能力。

PBL教学模式主要有以下特点：（1）以问题为教学的出发点，并将问题贯穿整个教学过程，学生的学习主要是通过问题进行构建的；（2）注重教学情境的创设，通过任务性教学活动提高学生分析问题和解决问题的热情；（3）体现学生的主体性，注重学生的独立思考与合作探究，是以学生自主学习为中心的教学模式。

二、数学关键能力——建模能力

数学建模能力是指学生在日常学习生活中发现问题并运用所学数学知识将实际问题抽象成数学问题，进而运用数学知识建立数学模型解决相关的数学问题，然后还原到实际问题中从而解决实际问题。数学建模能力的培养可以教会学生用数学的眼光发现问题，用数学的方法解决问题，可以极大地激发学生学习数学的兴趣，调动学生的学习积极性。正是学生主动地探索和研究，学生对数学知识的渴求度得到极大提升。

三、策略研究

PBL教学模式和数学建模活动都与解决现实生活问题紧密联系，都是以驱动型问题串作为主要的形式促使学生合作探究、动手实践，更多地关注学生学习的过程，而驱动型问题串的设置就要在合适情境下构建。我们尝试着从课上学生限时学习、课下学生拓展学习（选修课）、课外学生合作性学习这三方面做了探索。

（一）课上研讨，设置驱动型问题串

随着新教材的引入，建模能力的培养已经渗透进入教材，如每章的章前导语，以及每章最后的阅读材料或者拓展材料都提供了相关的实际问题背景，学生都十分感兴趣，如图2所示。

图2 阅读材料

章前导语正是这一章的起始课，当学生对要学的知识很茫然时，有了这种很好的问题背景，加上教师设置一系列的问题串，使学生带着问题继续后续的学习，而这些新的情境多是生活中真实发生的，学生的代入感比较强，可以调动学生的积极性。而学到的新知识也正是解决这些问题的数学模型。这样学生脑海里就形成了用数学知识解决实际问题的流程，即数学建模的流程。正是这样设置问题情境的问题串，使学生能带着问题思考，学生站位高，才能认识问题更深刻。

（二）开设校本课程，提高解决问题的能力

北京市第十五中学已经参加北京市高中数学建模比赛很多年，有很多学生在学校这种教学模式下，通过自身努力撰写的论文取得了很好的成绩。

例如，部分获一等奖数学建模论文如下：

《减少后视镜视觉盲区的探究》《大型汽车右后视镜的设计与摆放》《用小米手环探究跑步时对呼吸频率的影响》《关于双井桥路口东向路口交通拥堵状况的影响及其缓解方法的初探》《高峰时段西单站地铁换乘的优化选择》《出租车计价标准的合理性与优化》《教室LED照明规划与展望》《西单图书大厦收银台合理化配置》《函数模型在中国人脸型区分及对应发型选取》《信号控制交叉口左弯待转区设置的合理性分析》《手动跟踪太阳能光伏发电系统最大功率研究》，等等。

这些优秀论文所撰写的内容、解决的问题都是学生身边发生的事情，学生都能切身体会到。对高一、高二学生我们开设了论文研读课，通过阅读这些论文让他们自己感悟。素材很好，如何发挥出最佳效果呢？首先，我们将学生分组，每组至少四人形成学习的共同体。第一步，读懂论文；第二步，提出问题；第三步，评价论文并引发自己的想法。那么这三个环节中最关键的就是第一步，学生最先接触到的是论文的情境，根据情境每个学生各抒己见提出相关的问题，有的学生针对研究的价值和意义，有的学生针对解决问题的策略，有的学生针对数据的采集，有的学生针对采用的数学模型等。学生将这些问题汇总后，带着这些问题去研讨从而将论文彻底弄清楚。其次，学生对这个选修课很感兴趣，以小组形式汇报时很有感触和启发，为下一阶段的论文撰写打下基础。在这个过程中，学生带着问题在真实的情境下学习，极大地调动了学生学习数学的积极性，学生甚至会用批判式的眼光去看问题，极大地提高了他们分析问题、解决问题的能力。

（三）利用课下时间鼓励学生撰写数学建模论文

对学生而言，论文撰写难点是如何确定论文的题目。通过论文研读课他们很受启发，选题来源之一：用同样的方法研究与其相似的问题。选题来源之二：换个视角、增加问题的复杂性，进一步研究相关的问题；学生在深入学习之后，思路逐渐打开，视野逐渐放大，关注筛选热点问题、现实问题、身边问题。选题来源之三：用数学的眼光观察世界，发现研究的新问题。题目方向确定后，教师鼓励学生首先撰写论文提纲，提纲内容主要是设计成驱动型的问题串形式，如情境是什么，问题是什么，如何采集数据、数据处理、数学模型？……学生在解决这一系列问题过程中也就将自己的论文整体流程梳理得清晰明了，论文撰写也就水到渠成了。

正是通过这种课上教师设置问题情境，合理设置驱动型问题串，学生积极学习，选修课研读优秀论文，学生巩固丰富自己的能力，课下运用掌握的方法和策略完成建模论文，从而极大地提升了数学建模的能力，提升学生解决问题的能力。