潜没式高趾墙稳定抗力作用比系数预测的多元非线性回归模型

狄 鑫，孙淑华

（1.辽宁省水利水电科学研究院有限责任公司，辽宁沈阳，110055；2.安徽省合肥市肥西县柿树岗乡人民政府，安徽合肥，231200）

0 引言

在面板堆石坝工程中，常采用混凝土高趾墙来解决趾板区地形、地质条件缺陷及坝肩溢洪道、电站进水口等水工建筑物的协调布置问题。已建成的吉音混凝土面板坝[1]、新疆察汗乌苏面板坝[2]、黄河公伯峡面板坝[3]、甲岩面板堆石坝[4]等，均采用了混凝土高趾墙作为补充结构形式，且均运行正常，取得了良好的效果。但国内外亦不乏高趾墙附近部位出现破坏的工程，最典型的案例是尼日利亚的希罗罗面板堆石坝，该坝在蓄水至最大坝高的65%时，漏水量突然增加，潜水检查后发现河床部位面板与高趾墙连接处产生了裂缝。有学者认为，希罗罗坝周边缝处面板开裂是由高趾墙在水压力作用下发生转动倾覆造成的。

在面板堆石坝运行期，高趾墙大多潜没在水下，受堆石压力、水压力、扬压力等荷载共同作用，工作条件较常规挡墙复杂。稳定计算中，堆石压力的合理确定对计算结果的可靠性影响很大，目前规范中没有对堆石压力的计算方法作出明确规定，只能参考类似规范，如SL 379—2007《水工挡土墙设计规范》[5]，但该类规范中表面荷载的形式与潜没式高趾墙是不同的，直接套用可能会得出错误的结果，进而影响高趾墙稳定抗力作用比系数。近年来，学者们对高趾墙的稳定计算做了相关研究：傅中志等[6]对潜没式高趾墙土压力与稳定计算方法进行了研究，但计算方法较为复杂，对设计人员要求较高；吉恩跃等对潜没式高趾墙土压力分布及变化规律进行了研究，表明了由传统土压力理论（如库伦理论）计算得到的高趾墙土压力与实际土压力差异显著，不宜用于高趾墙稳定和应力计算。

回归分析方法是一种探求变量之间关系的技术方式，回归分析又分为线性回归分析和非线性回归分析，目前关于线性回归分析的研究方法和应用已相对成熟[7-9]，非线性回归分析的发展相对滞后且缓慢，需要庞大且复杂的计算过程。随着计算机技术的进步和计算软件的迅速发展，非线性回归分析的研究和应用也得到了快速发展[10-12]。在非线性回归分析中，多元非线性回归分析是通过对多个变量组成的非线性回归方程拟合获得模型，其中，通过非线性最小二乘法估计获取模型的未知参数是最广泛的做法。目前，多元非线性回归模型运用广泛[13-17]，如建立任意时刻基础沉降量与填筑高度、弹性模量、压缩层厚度、时间之间的多元非线性回归模型，并采用现场实测数据进行验证，证实模型的普适性[18]。研究多因素（掺和料种类、水胶比、养护龄期、加速腐蚀剂）作用对钢筋混凝土握裹力的影响，建立多因素共同作用影响钢筋混凝土握裹力变化的多元非线性回归分析模型[19]。

为了给设计人员提供一种方便又准确地计算高趾墙稳定抗力作用比系数的方法，加快设计进度，提出了面板堆石坝运行期潜没式高趾墙稳定抗力作用比系数计算的多元非线性回归模型。具体来说，首先通过接触算法模拟高趾墙与墙后填土、面板与垫层的相互作用及面板与趾板间周边缝的力学特性，计算面板堆石坝整体结构在自重荷载、水荷载作用下的内力情况；其次，采用积分运算得到高趾墙墙后土压力，进而采用材料力学方法进行稳定计算，得到稳定抗力作用比系数；最终，进行大量计算探究高趾墙上游坡比、下游坡比、顶宽、高度对稳定抗力作用比系数的影响规律，在此基础上结合工程实际并基于预测模型，建立面板堆石坝运行期潜没式高趾墙稳定抗力作用比系数预测的表达式。

1 本构模型及参数

1.1 有限元模型

以国内某面板堆石坝工程为例，最大坝高251 m，坝顶宽度12 m，上游坡比1∶1.6，下游综合坡比1∶1.72。高趾墙高度50 m，上游坡比1∶0.2，下游坡比1∶0.7。采用有限元计算软件进行大坝施工及蓄水过程模拟，面板堆石坝计算模型见图1。计算模型左侧为上游，右侧为下游，模型被离散为20 455个单元、20 964个节点，模型主体采用四边形单元，过渡部分采用三角形单元。

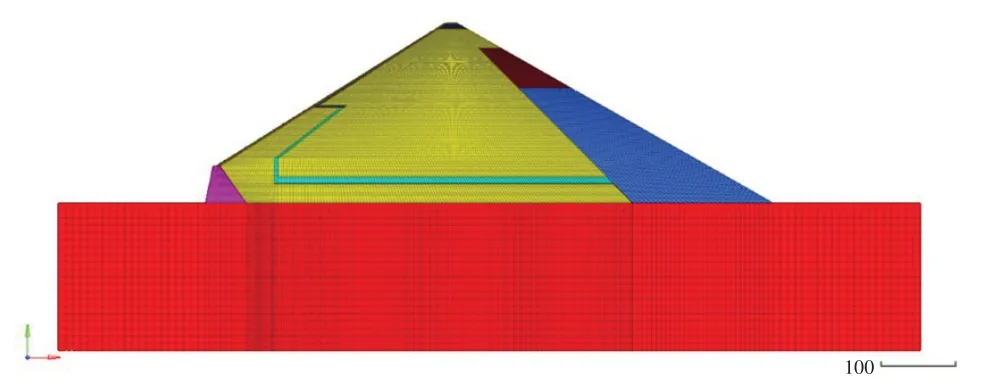
图1 有限元计算模型Fig.1 Finite element calculation model

1.2 本构模型及参数

土石坝设计规范中推荐采用邓肯-张（Duncan-Chang）E-B模型[20]计算面板堆石坝的应力变形特性，其中切线弹性模量Et表示为：

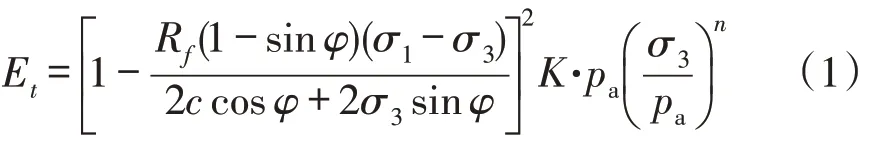
其中，σ1为第一主应力；σ3为第三主应力；K为切线模量基数；n为弹性模量指数；c为黏聚力；φ为内摩擦角；Rf为破坏比；pa为大气压力。卸荷状态下堆石料的弹性模量Eur可表示为：

其中，Kur为卸载弹性模量基数。切线体积模量Bt为：

其中，φ0为初始内摩擦角；Δφ为围压增加一个对数基数下内摩擦角的减小值。

高趾墙、面板、趾板及基岩采用线弹性模型，各材料的计算参数如表1所示。

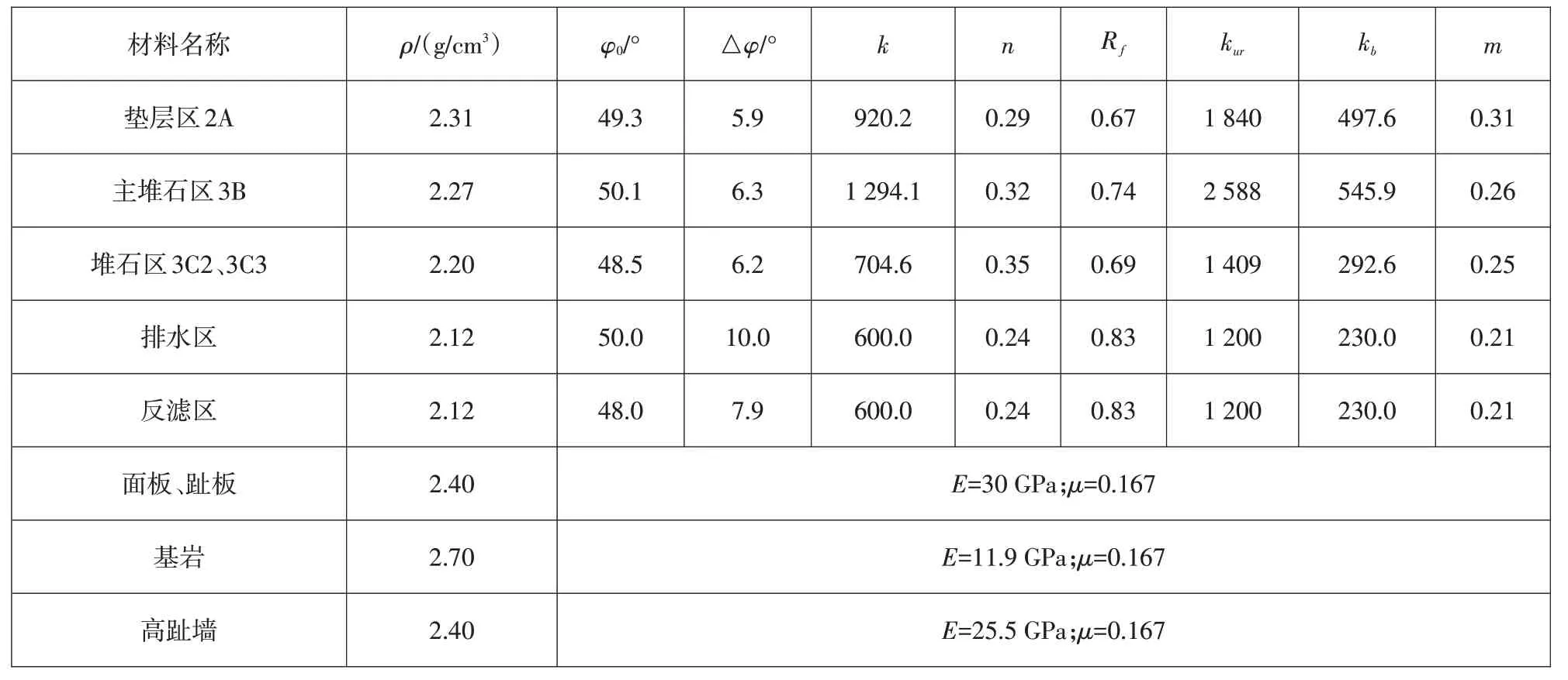
表1 材料计算参数Table 1 Material calculation parameters

面板与垫层、高趾墙与堆石料间相互作用采用Goodman单元模拟计算参数，见表2。Goodman单元模型是由Goodman等人提出的一种力学模型，在节点力{F}e作用下，两片接触面间的内力为：

表2 Goodman接触面单元模型参数Table 2 The parameters of Goodman contact surface element model

相应得两片接触面之间产生的相对位移为：

其中，τ为接触面上的剪应力；σn为正应力；ωs为相对剪切位移；ωn为法向位移。

在线弹性假定下，应力与相对位移成正比，关系式为：

其中，ks和kn分别为切向和法向的单位长度劲度系数，由试验确定，对于弹性材料为常量，若材料具有非线性特性，则为变量。

对于切向劲度系数ks，目前国内普遍采用克拉夫和邓肯等人依据直剪试验所提出的τ～ωs双曲线模型来确定，公式为：

其中，τ为接触面上的剪应力；ωs为相对剪切位移；a、b为决定接触面特性的试验参数。

克拉夫和邓肯认为剪应力和相对剪切位移之间符合双曲线关系，则ks1、ks2表示为：

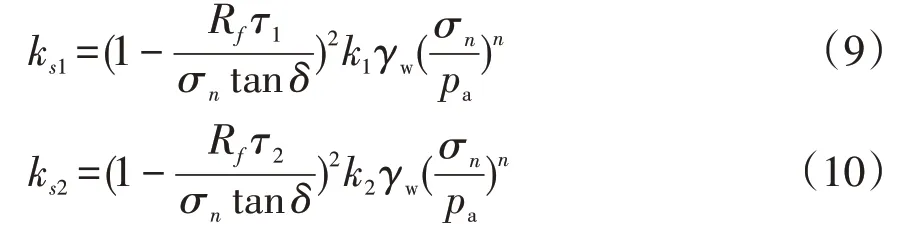
其中，k1、k2、Rf、n为非线性指标，通过试验确定；τ1、τ2为相应方向的剪应力；δ是接触面的界面摩擦角；γw是水的容重；pa是大气压。

该平面应变模型边界条件为：约束基岩底部节点x、y方向位移及基岩侧向x方向位移。

2 高趾墙参数对稳定抗力作用比系数的影响规律

采用控制变量法，研究各参数对稳定抗力作用比系数的影响规律。

（1）上游坡比：上游坡比影响高趾墙结构自重、水压力分布，从而影响稳定抗力作用比系数。因此，取上游坡比分别为1∶0.0、1∶0.2、1∶0.4，控制高趾墙高度50 m，顶宽10 m，下游坡比1∶0.9进行分析，得到规律如图2所示。由图2可知，稳定抗力作用比系数与上游坡比呈线性关系，稳定抗力作用比系数随上游坡比增大而增大。

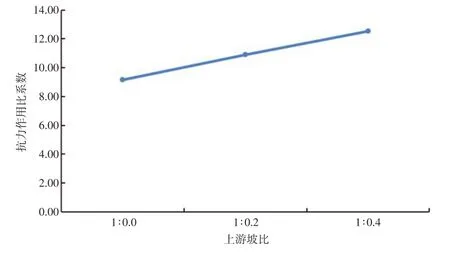
图2 稳定抗力作用比系数与上游坡比关系Fig.2 Relationship between ratio coefficient of stability resistance and upstream slope ratio

（2）下游坡比：下游坡比影响高趾墙结构自重、土压力分布，从而影响稳定抗力作用比系数。因此，取下游坡比分别为1∶0.9、1∶0.7、1∶0.5，控制高趾墙高度50 m，顶宽10 m，上游坡比1∶0.0进行分析，得到规律如图3所示。由图3可知，稳定抗力作用比系数与下游坡比呈线性关系，稳定抗力作用比系数随下游坡比减小而减小。

图3 稳定抗力作用比系数与下游坡比关系Fig.3 Relationship between ratio coefficient of stability resistance and downstream slope ratio

（3）顶宽：顶宽影响高趾墙结构自重、顶面水压力，从而影响稳定抗力作用比系数。因此，取顶宽分别为10 m、15 m，控制高度50 m，上游坡比1∶0.0，下游坡比1∶0.9进行分析，得到规律如图4所示。由图4可知，稳定抗力作用比系数与顶宽呈线性关系，稳定抗力作用比系数随顶宽增大而增大。

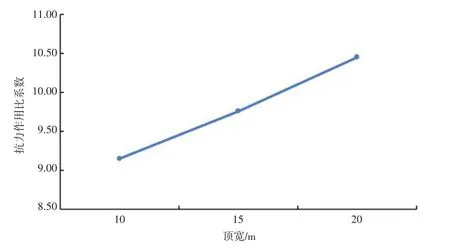
图4 稳定抗力作用比系数与顶宽关系Fig.4 Relationship between ratio coefficient of stability resistance and crest width

（4）高度：为了方便工程人员应用，本研究以堆石坝高度与高趾墙高度之比的表达方式来描述高趾墙高度。高趾墙高度影响高趾墙结构自重、土压力分布，从而影响稳定抗力作用比系数。因此，取高趾墙高度分别为50 m、60 m和80 m，即堆石坝高度与高趾墙高度之比分别为5、4和3，顶宽10 m，上游坡比1∶0.2，下游坡比1∶0.7进行分析，得到规律如图5所示。由图5可知，稳定抗力作用比系数与高度呈非线性关系，稳定抗力作用比系数随高度增大而增大。

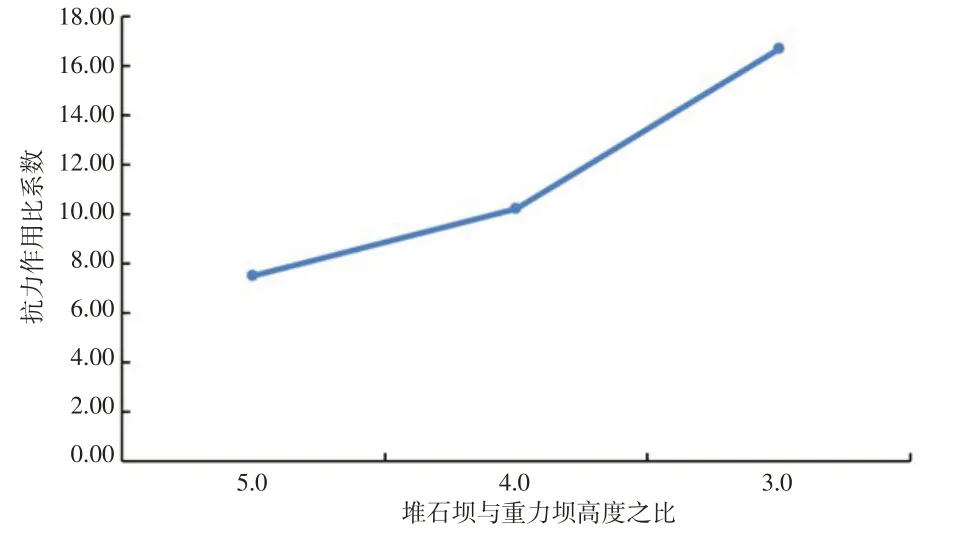
图5 稳定抗力作用比系数与高度关系Fig.5 Relationship between ratio coefficient of stability resistance and height

3 多元非线性回归模型

由上述分析可知，高趾墙高度、上游坡比、下游坡比、顶宽这4个因素都对高趾墙稳定抗力作用比系数影响显著。采用最小二乘法估计方法，建立影响因素与稳定抗力作用比系数间的非线性函数关系式。

高趾墙上游坡比、下游坡比、顶宽与稳定抗力作用比系数呈线性函数关系，所以稳定抗力作用比系数与高趾墙上游坡比、下游坡比、顶宽间的函数关系如下：

式中，y为稳定抗力作用比系数；x为上游坡比、下游坡比或顶宽，顶宽单位为m；k为系数。

堆石坝高度与高趾墙高度之比和稳定抗力作用比系数呈非线性函数关系，所以稳定抗力作用比系数与高度比的函数关系如下：

式中，y为稳定抗力作用比系数；x为堆石坝高度与高趾墙高度之比；k、n为系数。

高趾墙高度、上游坡比、下游坡比、顶宽这4个因素共同作用于稳定抗力作用比系数这一变量，并且4个自变量之间互相影响，为最大程度还原和模拟因变量与自变量间的函数关系，将函数形式设为：

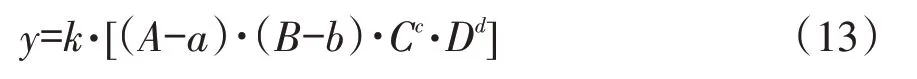
式中，y为稳定抗力作用比系数；A为堆石坝高度与高趾墙高度之比；B为上游坡比；C为下游坡比；D为顶宽，单位为m；a为堆石坝高度与高趾墙高度之比参数；b为上游坡比参数；c为下游坡比参数；d为顶宽参数；k为总体回归参数。

4 稳定抗力作用比系数预测

将不同类别的设计参数排列组合，形成36组水平组合，见表3。将表3中每一组水平组合作为高趾墙的几何参数，基于已建好的有限元模型进行计算，通过积分计算获取墙后土压力，进而采用有限元提取土压力计算高趾墙的稳定抗力作用比系数。将表3中的前30组样本作为模型拟合样本，以尽可能提高模型的精度；将后6组样本作为预测样本，对模型进行精度检验。

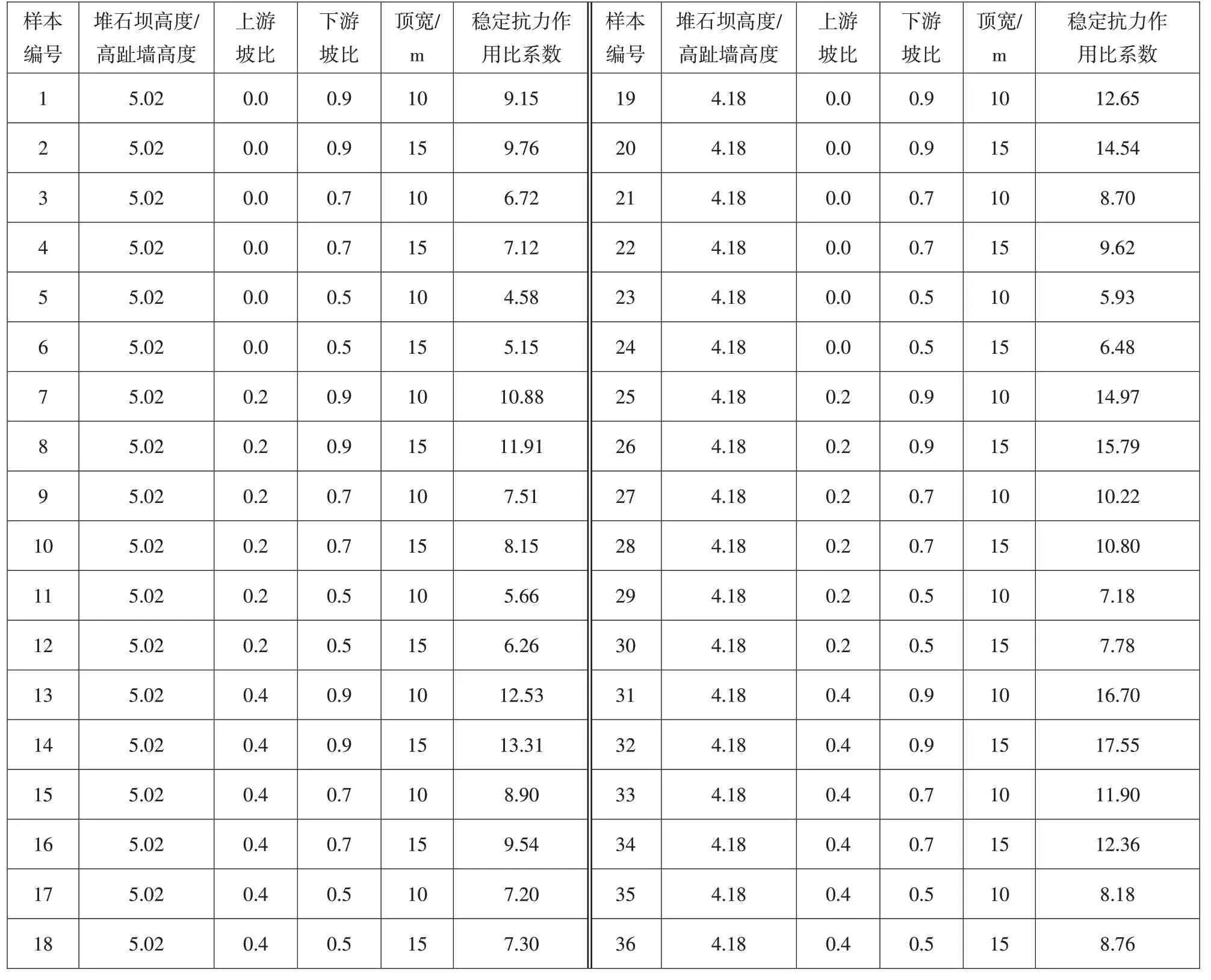
表3 设计参数组合样本Table 3 Samples of design parameters

对样本中的30组数据非线性拟合，根据最小二乘法建立稳定抗力作用比系数与4个因素的预测模型为：

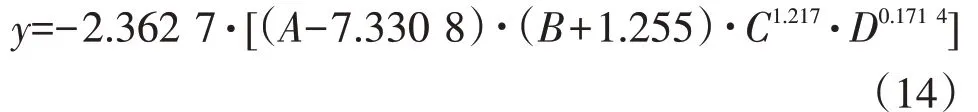
对该模型进行回归分析，计算得均方误差为0.210 4。利用函数返回得到置信度为95%的参数置信区间见表4。置信区间较窄，且不包含0，说明各个因素影响均不可或缺，模型较好。

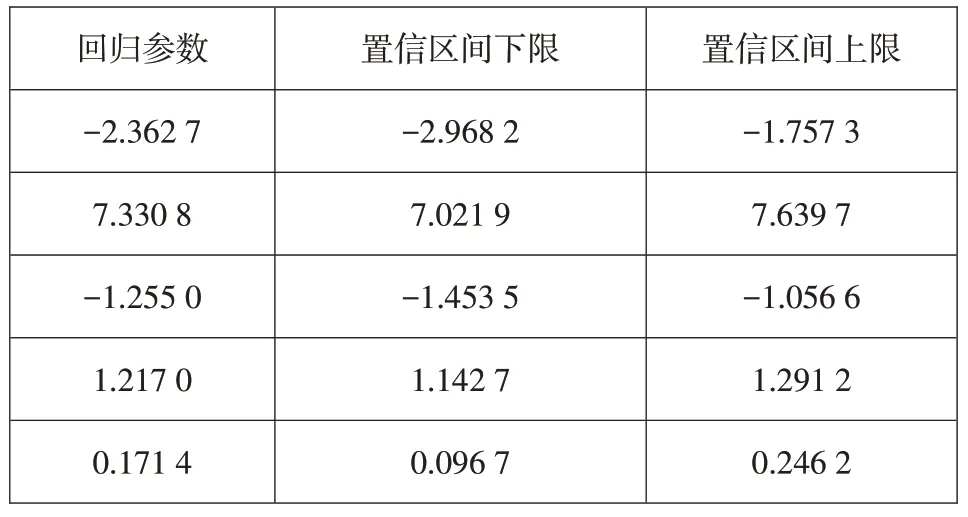
表4 回归参数置信区间Table 4 Confidence intervals of regression parameters

对该预测模型进行相关性分析，回归系数为0.991 8，说明该预测模型对数据拟合的效果较好。

由式（14）计算所得的稳定抗力作用比系数与真实值的对比见图6。由图中两曲线的对比可看出，该多元非线性回归模型的拟合效果较好。

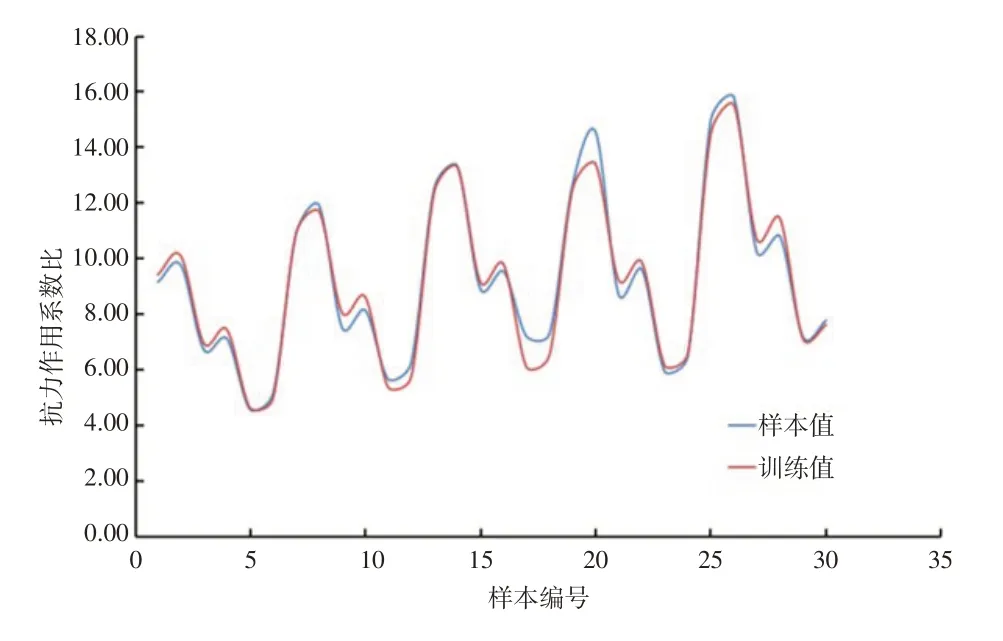
图6 多元非线性回归模型拟合效果对比Fig.6 Comparison of fitting effect of the multivariate nonlinear regression model

利用该非线性回归模型对6组样本进行预测，预测值与真实值对比见图7。由图7可知，该回归模型的预测结果较为准确。

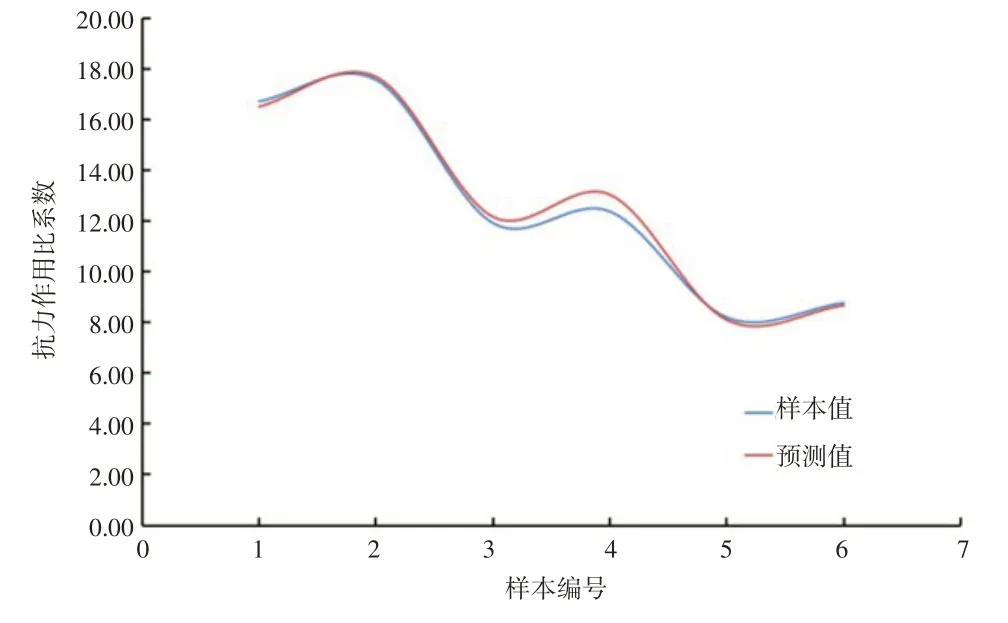
图7 多元非线性回归模型预测结果拟合曲线Fig.7 Fitting curves of prediction results of the multivariate nonlinear regression model

针对多元非线性回归模型的拟合样本和预测样本，计算预测绝对误差与相对误差，见表5。结果表明，36组样本的平均预测绝对误差为0.25，平均预测相对误差为2.02%，说明模型的预测精度较高。可见多元非线性回归模型的预测结果与真实值误差较小，在实际工程中，可以满足初设阶段设计人员对高趾墙稳定抗力作用比系数预测精度的要求。

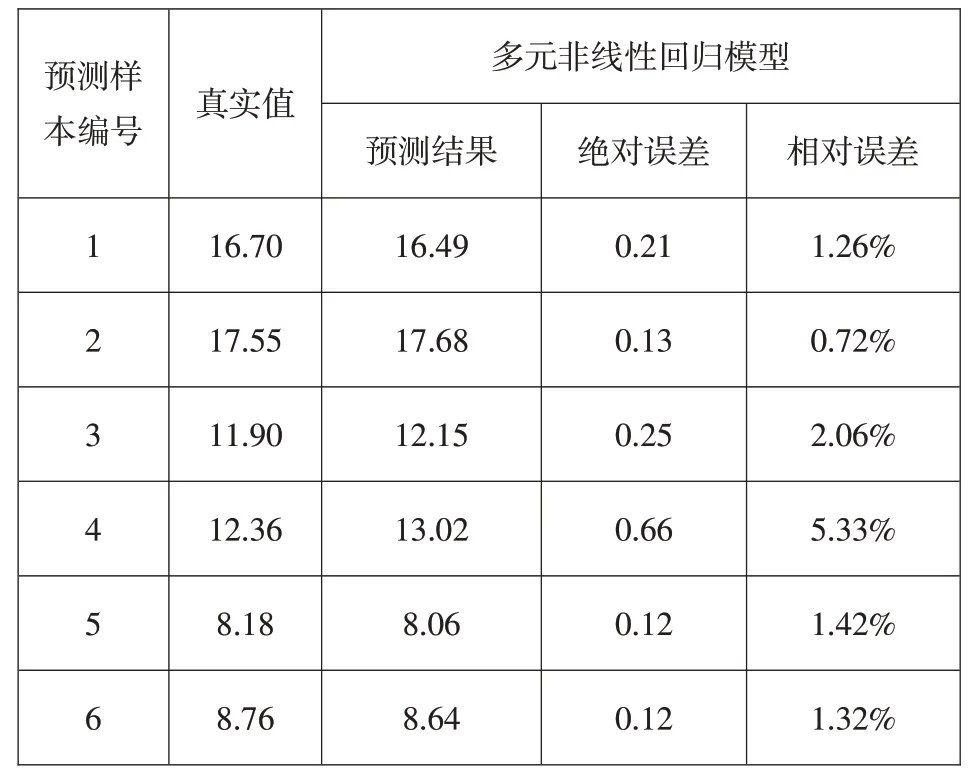
表5 预测样本的预测结果及误差Table 5 The results and errors of prediction samples

5 结语

基于大样本的有限元数值模拟，获得复杂受力及接触效应下高趾墙的稳定抗力作用比系数。具体来说，通过接触算法模拟高趾墙与墙后填土、面板与垫层的相互作用及面板与趾板间周边缝的力学特性，计算面板堆石坝整体结构在自重荷载、水荷载作用下的内力情况。采用积分运算得到墙后土压力，进而采用材料力学方法进行稳定计算，得到抗力作用比系数。探究高趾墙上游坡比、下游坡比、顶宽、高度对稳定抗力作用比系数的影响规律，研究发现，稳定抗力作用比系数与上游坡比、下游坡比、顶宽呈线性关系，而与高趾墙高度呈非线性关系。在此基础上，采用多元非线性回归分析方法得到面板堆石坝运行期高趾墙稳定抗力作用比系数预测模型，通过本研究样本的回归分析表明，所建立的预测模型回归系数较高，达到0.9以上，均方误差较小。36组样本的平均预测相对误差为2.02%，预测精度较高。整体而言，本研究所构建的用于潜没式高趾墙稳定抗力作用比系数预测的多元非线性回归模型，较为合理地反映了各个因素对稳定抗力作用比系数的影响关系，且形式简洁，便于工程应用，为初设阶段高趾墙设计参数的确定提供了简捷算法，加快了设计进度。