湖北强降水频次时空特征及基于GWR模型的地形关系分析

2022-08-24谌伟刘佩廷徐枝芳徐迎春杨海鹏

热带气象学报 2022年2期

谌伟，刘佩廷，徐枝芳，徐迎春，杨海鹏

(1.武汉市气象局，湖北武汉 430048；2.中国气象局武汉暴雨研究所/暴雨监测预警湖北重点实验室，湖北武汉 430205；3.国家气象中心，北京 100081)

1 引言

湖北省地处长江中游，属典型的东亚季风气候，每年汛期降水过程频繁，既有范围大、持续时间长的梅雨降水，又多发尺度较小的局地短时强降水，是强降水事件显著活跃的几个地区之一[1-2]。同时地貌多样，山地、丘陵、岗地、平原兼具，强降水的时空分布也受到地形影响。作为拥有最长长江干线省份，湖北防汛一直是大事，摸清强降水精细化演变特征及其与地形的关系对防汛工作至关重要，对防洪调度极其关键。

随着逐小时降水资料的积累，学者们在小时降水的时间变化、空间分布、持续性特征等方面取得了众多成果。由于不同历时的降水事件所突出的主要天气系统、影响机制也不一样，部分学者已按照降水持续时间的长短分类进行降水演变的精细化研究，如Yu等[3-4]、李建等[5]、计晓龙等[6]将降水事件分为长历时(＞6 h)和短历时(1～3 h)两类；戴泽军等[7]则按持续时间1～4 h、5～10 h、＞10 h分降水事件为三类；原韦华等[8]、梁苏洁等[9]将持续时间在6 h以上的降水事件记为持续性降水事件，而持续时间小于等于6 h的降水事件为短时降水事件；杨萍等[10]将北京夏季降水进行了长、中、短历时划分。但是，不将普通降水剔除仍会掩盖强降水信息的某些细致特征，针对强小时雨强，学者们对长江上游地区研究较多[11-18]，而长江中游相对匮乏。

影响降水空间分布的因素较多，其中地形相对定常，学者们多建立数学回归模型来定量分析降水与地形关系，如傅抱璞[19]建立半经验理论抛物线模式，蒋忠信[20]提出高斯曲线模式修正，俞洁等[21]则进一步完善为三参数高斯模式拟合曲线，舒守娟等[22]在中国区域应用偏最小二乘法，罗琦等[23]、周学云等[24]、周秋雪等[12]采用一元或多元线性回归拟合，等等。传统的线性回归为全局回归方法，只能反映区域整体上的平均拟合，难以刻画多中小尺度复杂地形影响。考虑到地理加权回归GWR(Geographically Weighted Regression，下文简称GWR)模型，可将传统的线性回归在空间展开，建立空间范围内每个站点的局部线性回归方程，描述降水的空间非定常性和局地变化，并通过控制回归的空间尺度，提高拟合优度，减少回归模型中的不可解释方差，近年来有学者已运用GWR回归模型定量研究降水与地形因子之间的关系[25-27]。

本文利用35年(1983—2017年)湖北省汛期(5—9月)逐小时降水资料，剔除一般降水，按强降水事件持续时间的长、短历时分类研究强降水频次时空特征，并运用OLS、GWR回归模型探讨强降水频次与地形海拔高度、坡度之间的关系，提高强降水事件演变规律的精细化认识。

2 资料与方法

2.1 数据来源与处理

湖北省西、北、东三面高起，中部向南敞开，长江、汉江两大河流穿行其间，“马蹄”状大地形下又孕育出较复杂的中小尺度地形，国家观测站点均匀分布其中(图1)。考虑到各站点数据资料的完整、连续，本文降水数据选定1983—2017年湖北省74个国家气象观测站的逐小时降水资料集进行分析，该数据来源于湖北省信息与技术保障中心，经过气候极值等质量控制。地形数据采用SRTM(Shuttle Radar Topogra-phy Mission)数字高程模型数据(Digital Elevation Model,DEM)、SRTM坡度数据等，分辨率为90 m，获取于地理空间数据云(http://www.gscloud.cn/)，每个站点地形数据(海拔高度、坡度)用其10 km半径范围内的所有SRTM格点数据平均值代表。

图1 湖北省气象观测站及其地形空间分布单位：m。

2.2 强降水事件定义与分类

本文定义强降水事件为单站一次降水过程有≥20 mm/h强降水发生，事件开始前、结束后至少2 h内没有降水，开始至结束的小时数为事件持续时间≤24 h[17]。强降水频次指统计时段内发生降水量≥20 mm/h次数。这里将湖北汛期强降水事件分为长历时(＞6 h)、短历时(1～6 h)两类进行时空特征分析。

2.3 普通最小二乘法回归模型

普通最小二乘法(Ordinary Least Squares，下文简称OLS)是统计分析中较常使用的一种全局回归方法。公式如下：

其中Y为因变量，Xi为自变量，βi为回归系数，ε为误差项。分别以湖北站点长、短历时强降水事件强降水频次(下文简称长、短历时强降水频次)为因变量Y，站点海拔高度、坡度为自变量X1、X2，构建长、短历时强降水频次的OLS模型。模型分析结果，能够描述湖北区域强降水频次受地形因子影响的总体情况，可评估各项数据能否适用于GWR模型。

2.4 地理加权回归模型

地理加权回归GWR不同于传统的OLS、多元等全局回归方法，能够解释估算点位置变化带来的空间非定常性，通过为估算点设计一个权重矩阵，根据样本与估算点之间的距离进行权重分配，距离越近，权重越大，以此来捕获估算点r半径范围内变量间关系的局部变化，可以调节拟合半径r来校准模型。GWR公式如下：

其中i为代表站点，(ui，v j)代表站点i的坐标，ui、v j即投影坐标系下的横、纵坐标位置，yi为因变量，k为独立自变量，xik和εik分别为i站点的第k个自变量和残差，βo为截距，βi为回归系数。回归系数随空间位置变化如下：

式中X为独立自变量矩阵，W(ui，v j)为第i个估算站点的空间权重矩阵，反映周围样本站点对估算站点的影响。W(ui，vj)由空间权重函数计算，这里采用高斯函数作为权重核函数：

其中dij为站点i、j之间的距离，b为带宽(即模型回归半径)，由Akaike信息准则(Akaike Information Criterion，AICc)最小化矫正确定最优带宽，这里选取100 km，分别以湖北站点长、短历时强降水频次为因变量yi，站点海拔高度、坡度为自变量xi1、xi2，构建长、短历时强降水频次各自的GWR模型，拟合每个站点强降水频次与地形因子之间的定量关系。模型计算结果需剔除干扰站点，一是回归半径内站点数少于3的估算站点，二是回归半径内最低与最高格点海拔高度差低于300 m的估算站点，三是回归半径内最低与最高格点坡度差低于10°的估算站点。

3 结果分析

3.1 长、短历时强降水频次年际变化特征

图2给出了湖北汛期长、短历时强降水事件逐年强降水频次(简称长、短历时强降水年频次)，可以发现：(1)长历时强降水年频次变化幅度远高于短历时，不仅低频年极值更低(2001年，79次)，而且高频年极值更高(1998年，294次)；(2)长、短历时强降水年频次变化分布不具有较好的一致性趋势，相关度较低，在35年中有14年增减趋势相反。上述现象应该与长、短历时强降水的生成原因有关，长历时强降水主要由较大尺度的系统性强降水过程造成，而短历时强降水则包含众多中小尺度局地热对流，很明显前者年频次与降水多寡年份相关度更高，而后者受其影响较低。

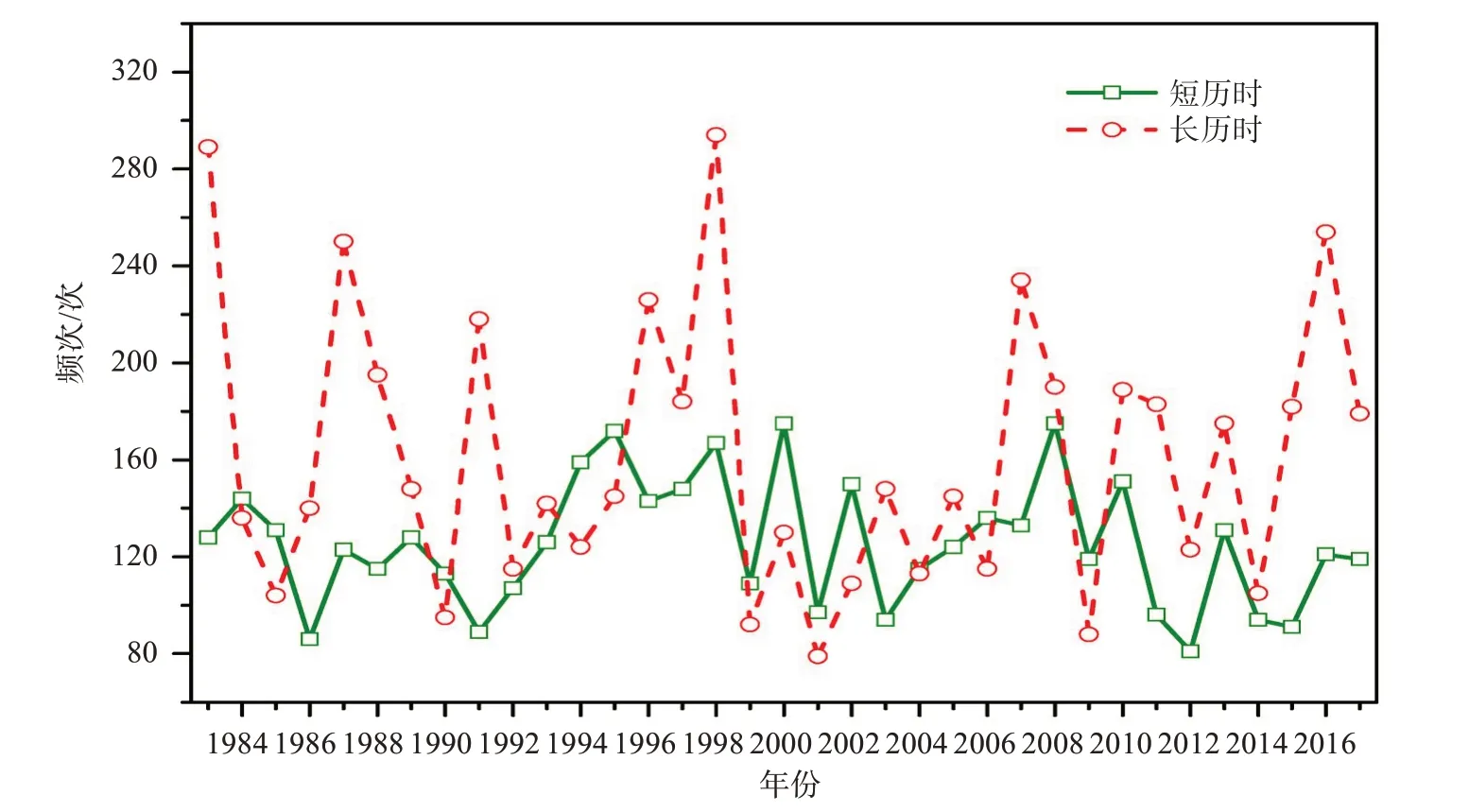
图2 湖北汛期长、短历时强降水年频次逐年变化图

将湖北汛期长、短历时强降水年频次进行Morlet小波转换(图3)。可以发现，湖北汛期长、短历时强降水年频次周期变化明显，正负值中心交替显著，年代际变化(≥10 a)存在1个主振荡模态，长历时周期为准10年、短历时为10～14 a；年代际以下尺度(＜10 a)存在2个主振荡模态，周期为4～6 a和准2 a。值得注意的是，短历时强降水年频次年代际变化周期相对于长历时表现更显著和稳定，而年代际以下尺度则反之。年代际周期变化，长历时强降水年频次大致经历了1985—1987年、1996—1998年、2006—2008年、2016—2017年4个偏多期，短历时强降水年频次则为1983—1985年、1994—1998年、2006—2010年3个偏多期。4～6 a年际变化尺度，长历时强降水年频次大致经历了1983年、1986—1987年、1991—1992年、1996—1998年、2002—2003年、2006—2007年、2011—2012年、2015—2017年8个偏多期，短历时强降水年频次则为1983—1985年、1988—1989年、1993—1995年、2000—2002年、2007—2009年、2015—2017年6个偏多期。

图3 湖北汛期长(a)、短(b)历时强降水年频次小波变换实部图实线和虚线分别为正、负值。

3.2 长、短历时强降水频次旬变化特征

湖北汛期长、短历时强降水事件逐旬强降水35年总频次(简称长、短历时强降水旬频次，图4a)反映，长、短历时强降水旬频次从5月中旬开始都存在一个急剧增长又减少的变化过程。长历时强降水旬频次在6月下旬出现一次跃升，7月上旬增长至顶峰，之后开始减少；短历时强降水旬频次则有两次跃升，分别在6月下旬和7月中旬，至8月上旬达到峰值。此外，7月上旬以前长历时强降水旬频次都远超短历时，而7月中旬至整个8月短历时强降水旬频次则反超长历时。而湖北夏季通常分为初夏、梅雨季、盛夏三个时段，从常年平均看6月16日入梅、7月8日出梅。可以看出，长、短历时强降水旬频次在6月下旬和7月中旬的大幅增长与梅雨季、盛夏到来有关。梅雨期降水过程多阻塞形势，强降水范围大、持续时间长，易形成长历时强降水事件；盛夏，副高经常控制湖北大部，长江中游一带高温高湿，午后到傍晚热力条件最旺盛时易产生局地雷雨天气，强度大、持续时间短，多形成短历时强降水。

3.3 长、短历时强降水频次日变化特征

图4b给出了湖北汛期长、短历时强降水事件逐时强降水频次，日变化曲线展示出显著的单峰结构特征。长历时强降水频次日变化曲线波谷(11时，北京时间，下同)临近中午，此后一路攀升至夜间21时达到顶峰，并在峰值附近维持到凌晨03时，之后下降；短历时强降水频次日变化曲线极低值出现在上午09时，12时以后频次增多，峰值出现在下午17时，20时以后急剧减少。长历时强降水频次日变化曲线相较短历时，峰值时段持续时间更长，低值维持时段更短，夜发性特征突出，短历时则主要发生于午后到傍晚时分。通常认为，太阳辐射日变化会使午后到傍晚大气层结更加不稳定[28]，有利于热对流发生，对应短历时强降水；而长历时强降水事件的夜发性因素较多，夜晚云顶辐射降温导致大气不稳定[29]、边界层内非地转风的惯性振荡导致夜间西南低空急流增强[30-31]、山地与平原之间的夜晚温度差异变大会强迫出局地热力环流[32-33]等。

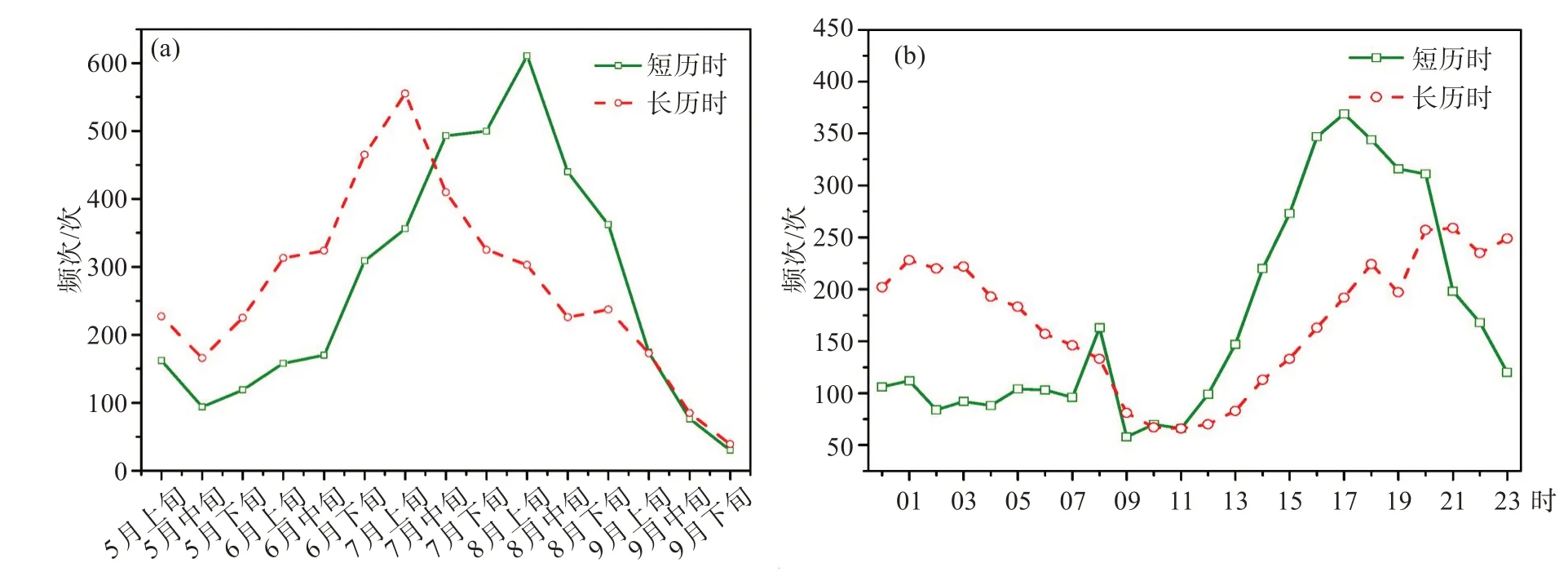
图4 湖北汛期长、短历时强降水35年总的旬频次(a)和日变化(b)

3.4 长、短历时强降水频次空间分布特征

图5给出了1983—2017年(5—9月)湖北站点长、短历时强降水频次空间分布，长、短历时强降水高频次站存在聚集性特点。短历时强降水高频次站(≥70次)主要分布于鄂西山地与江汉平原之间的斜坡式过渡带、大别山与幕阜山之间(即长江干流地带的武汉-黄石地区)、大别山东麓西侧和幕阜山北侧等地，其中极大频次位于咸宁赤壁站，达98次。长历时强降水高频次站(≥100次)更为集中，主要在大别山西麓南侧、幕阜山北侧，最大频次为黄冈红安站，达141次。

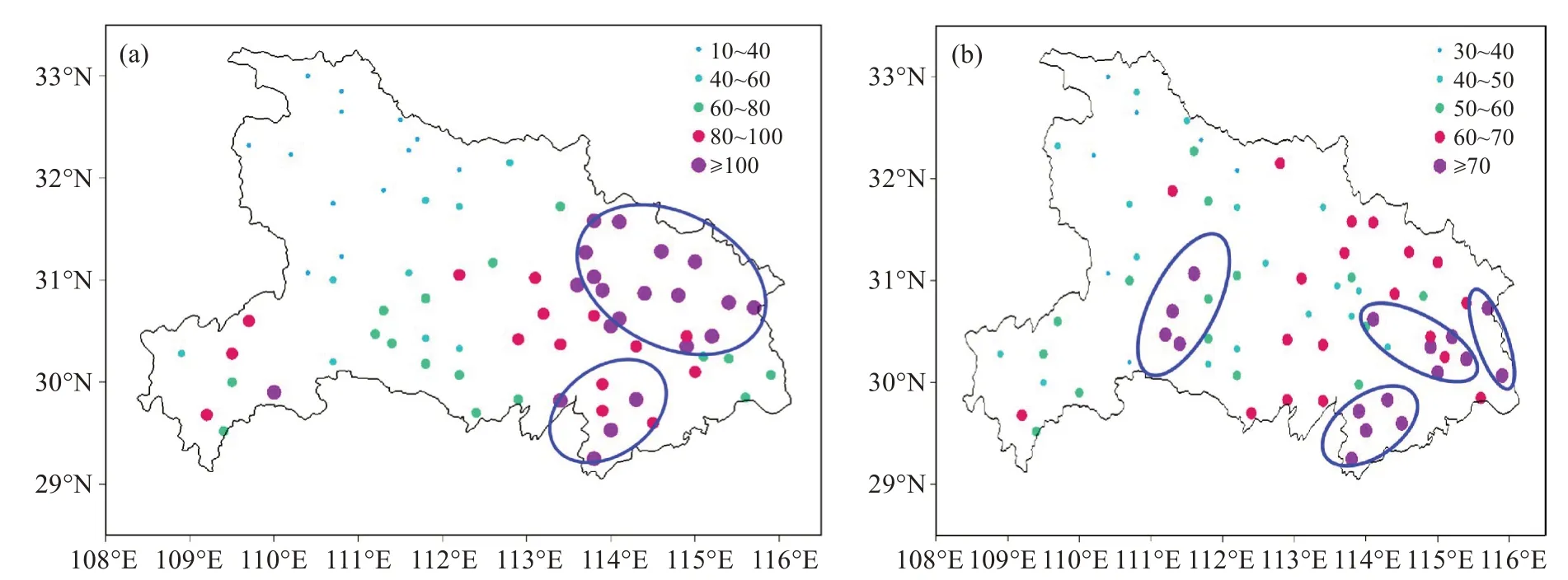
图5 湖北站点长(a)、短(b)历时强降水频次的空间分布

从长、短历时强降水频次的空间分布可以发现，高频次站点多出现在特定地形条件下，如大别山与幕阜山之间、鄂西山地到江汉平原的斜坡式过渡地带、大别山南侧或西侧、幕阜山北侧等。夏季地面，大别山与幕阜山之间、大别山南侧、鄂西山地到江汉平原的斜坡式过渡地带存在准定常的中尺度辐合线或涡旋[34]，另外，气流会顺着长江、沮水从江汉平原深入鄂西山地，受到地形抬升以及“峡管”加速，而大别山南侧、幕阜山北侧对西南气流也有阻挡抬升，这些在不稳定能量充足的情况下均可触发对流的发生形成短历时强降水，当高空有西风或者东风波槽叠加时，对流将进一步发展加强，影响范围和持续时间增加，有利于长历时强降水形成，如西风带低槽引导的对流系统行至大别山南侧时，雷暴出流会被阻挡并迫使东移的中尺度对流系统(MCSs)出现后向传播，造成长时间的区域性长历时强降水[35-37]。

3.5 基于回归模型的强降水频次与地形关系

3.5.1 OLS模型结果

OLS(最小二乘法)解释变量系数(表1)反映海拔高度与短历时强降水频次整体呈负相关，坡度与之呈正相关，坡度大于海拔高度的系数绝对值说明坡度对强降水频次的影响更大。VIF为4.711，小于7.500，没有冗余解释变量。Koenker(BP)统计量、联合F统计量、联合卡方统计量自由度均为0.00，表明OLS模型具有显著性。Jarque-Bera统计量为1.92，大于0.05，也表明OLS为有统计显著性非稳态的回归模型，可进行GWR分析。长历时强降水频次与海拔高度、坡度均呈负相关(表2)，且地形坡度对强降水频次的负影响更大，Jarque-Bera统计量为1.27，OLS统计模型也具有显著性。进一步分析OLS回归模型全局拟合系数，无论长、短历时，R2和R2Adjusted值都较低，均不超过0.2，说明模型虽然构建成功，但是不能较好地解释强降水频次与复杂地形因子之间的关系；散点图显示(图6)，长、短历时强降水频次在拟合线上下分布均过于散乱，也证实传统全局线性回归方法的不适用。

表1 短历时强降水频次OLS结果汇总

表2 长历时强降水频次OLS结果汇总

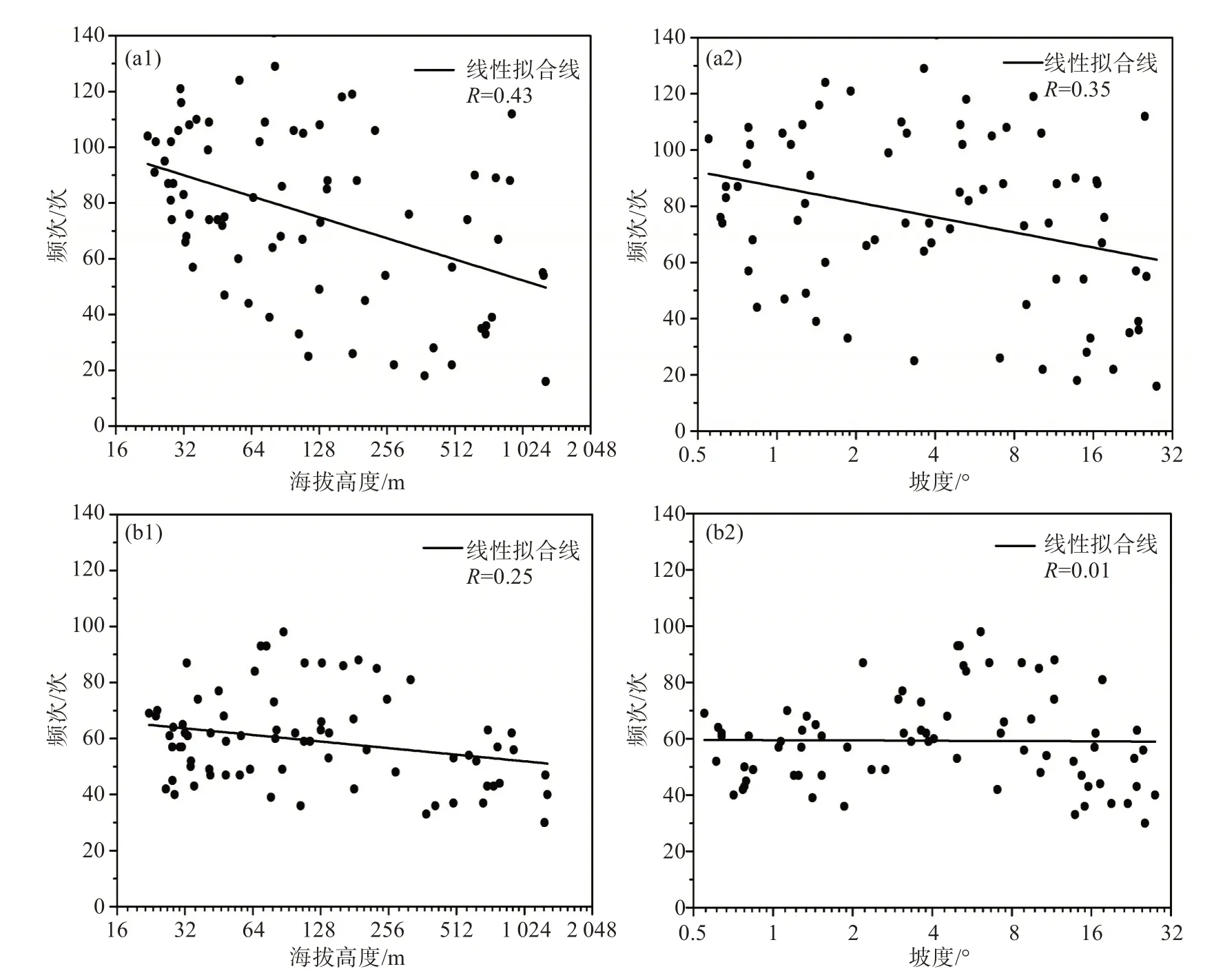
图6 长(a)、短(b)历时强降水频次与海拔高度(1)、坡度(2)的散点图

3.5.2 GWR模型结果

首先分析GWR模型估算结果评价指标(表3)。相比OLS模型，GWR模型R2和R2Adjusted值有了大幅提升，长历时分别为0.77、0.71，短历时分别为0.64、0.54；修正的AICc是诊断模型性能的一种度量，越小越好，这里显示GWR长、短历时值均较OLS低；残差平方和为观测所得值与模型估算值之间差值的平方和，也是越小越好，GWR长、短历时值远小于OLS。所以，GWR回归模型拟合强降水频次与地形因子之间的定常关系效果有了明显的改善。

表3 OLS、GWR模型估算结果评价指标

其次分析强降水频次与地形因子的GWR回归系数。从长历时看(图7a、7b)，强降水频次与海拔高度的正相关主要在鄂东，回归系数的正值中心位于大别山东麓西侧，其中黄梅站达到0.41次/米，负相关分布在广阔的湖北中西部，负值中心位于大别山西麓南侧，其中广水站达到-0.30次/米，35%站点回归系数通过了0.05或0.01显著性T检验；强降水频次与坡度的回归系数分布则相反，正相关在湖北中西部，正值中心位于大别山西麓南侧，广水站达到5.71次/度，负相关在鄂东，负值中心位于大别山东麓西侧，其中英山站达到-7.00次/度，通过显著性检验站点更少(20%)。从短历时看(图7c、7d)，通过显著性检验站点更多(70%左右)，但鄂西站点通过稀少，强降水频次与海拔高度均是负相关，负值中心在大别山东麓西侧、武汉-黄石地区，武汉站达-0.20次/米；强降水频次与坡度除鄂西个别站点都是正相关，正值中心也在大别山东麓西侧、武汉-黄石地区，武汉站达6.43次/度。

3.5.3 GWR模型结果分析

回归模型结果发现：(1)湖北中东部站点回归系数，短历时通过显著性检验远超长历时，说明大别山、幕阜山、大洪山等山脉组成的中小尺度地形结构对主要由较大尺度天气系统形成的长历时强降水影响较小，但对包含大量热对流等较小尺度短历时强降水影响更广，符合崔春光等[38]数值模拟1998年鄂东梅雨期沿江特大暴雨认为地形未起较大作用的结论；(2)鄂西山地站点回归系数可信度较差，可能是模型样本数偏少和站点密度偏小；(3)大量的海拔高度与坡度回归系数成正、负反相关，既是两个自变量与因变量关系的真实反馈，也与模型仅有两个自变量，必然存在相互影响这一局限性有关；(4)海拔高度与长历时强降水频次在大别山东麓西侧正相关最大，在大别山西麓南侧负相关最大，大别山东麓西侧多为西南暖湿气流迎风坡，地形扰流和强迫抬升作用利于连续性强降水的形成，大别山西麓南侧多为西南暖湿气流左前侧区域，这里海拔高度越低越利于北方南下冷空气的渗入，也利于受大别山东麓阻挡的MCSs雷暴出流朝此处后向传播；(5)坡度与长历时强降水频次在大别山东麓西侧负相关最大，在大别山西麓南侧正相关最大，大别山东麓西侧地形坡度较大不利于较大水平尺度的中尺度系统发生发展[39]，而大别山西麓南侧在海拔不高的情况下，坡度变化越大，越有利于地面气流在此形成准常定的中尺度涡旋或辐合线；(6)海拔高度与湖北中东部短历时强降水频次均为负相关，白天山区盛行辐合性热力气流虽然利于短历时热对流的发生发展[40]，但是湖北三面环山、中部低洼，经常出现对流在山上发生，受环境风场作用向山下平原地带移动，当叠加准定常的中尺度低涡或辐合线时对流进一步发展加强，这也是海拔越低的武汉-黄石地区，短历时强降水频次反而越多的原因；(7)坡度对湖北短历时强降水频次的最大影响在大别山东麓西侧以及沿长江干流的武汉-黄石地区，一方面地形坡度越大越有利于大别山东麓西侧迎风坡较小尺度的中尺度对流系统生成[39]，另一方面更需关注的是武汉、黄石这些人口密集、经济发达的沿江低洼城市区域由于地形起伏也存在较大坡度变化(图7e、7f)，利于准常定的中尺度涡旋或辐合线形成，易触发、促进短时对流的发生发展。

图7 长历时强降水频次与海拔高度(a)(蓝色箭头为冷空气侵入路线，红色箭头为西南暖湿气流进入路线，红色、蓝色圆圈分别代表正、负值中心区)、坡度(b)(红色、蓝色圆圈分别代表正、负值中心区)和短历时强降水频次与海拔高度(c)(红色箭头为山地发生的局地对流通常向平原地区发展的路线，蓝色椭圆圈代表通过显著检验区)、坡度(d)(红色椭圆圈代表通过显著检验区)的回归系数空间分布以及武汉-黄石地区海拔高度(e)与坡度(f)的地形空间分布