基于S波段双极化雷达的变分法的定量降水估计算法

刘陈帅，张阿思，陈生

(1.中山大学大气科学学院，广东 珠海519082；2.广东省气候变化与自然灾害研究重点实验室，广东 珠海519082；3.热带大气海洋系统科学教育部重点实验室，广东 珠海519082；4.南方海洋实验室（珠海），广东 珠海519082；5.广东省气象台，广东 广州510641；6.中国科学院西北生态环境资源研究院黑河遥感站和甘肃省遥感重点实验室，甘肃 兰州730000)

1 引 言

上世纪七十年代，美国科学家提出了双极化雷达理论。经过数十年的发展，双极化雷达已经步入业务实用阶段[1-2]。定量降水估计（QPE）是雷达气象学的主要任务之一，与传统的多普勒雷达相比，双极化天气雷达在QPE上有着优异的表现。雷达测量误差是雷达QPE的主要误差之一，在进行QPE之前，应当对测量的极化变量进行重构以消除测量中的随机误差。

传统的QPE一般是通过水平反射率因子与降雨率（R）之间的幂律关系来反演降雨率。而双极化雷达相较于传统雷达，可以提供更多的信息如差分反射率因子（ZDR），比差分传播相移（KDP）和差分相位（ΦDP），极化变量受到雨滴谱数据的影响更小，因此用极化变量估计降雨率有更好的表现[3]。

差分相位（ΦDP）为水平和垂直极化信号传播相移的差分，比差分传播相移（KDP）是ΦDP关于距离的导数。与基于水平反射率因子ZH降水估计算法R(ZH)相比，基于KDP的降水估计算法R(KDP)受雨滴谱影响更小。KDP是雷达的间接产品，在进行定量降水估计之前需要对KDP进行估计，如下面的公式（1）：

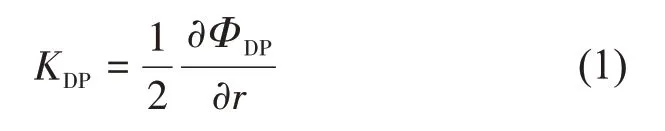
在实际应用中，传播中的随机误差和后向散射相位（backscattering phase）可能导致出现负值的KDP。Maesaka提出一种基于非负KDP的变分方法来估计ΦDP，通过计算边界条件，以测量值和理论值之间的误差为代价函数，通过逐次迭代来求解最优的KDP[4]。当径向数据中存在异常值或者大量连续缺失值时，Maesaka的方法不能准确求解出边界条件，进而导致错估KDP，而且计算边界条件的方法会损失较多的信息，本文设计了一种比较稳健的边界条件求解方法，在保留更多的信息情况下，得到准确的边界条件。

变分方法的优点就是在确定远-近边界条件后，可以有效地减小随机误差的影响，拥有较好的拟合效果，在加入低通滤波器的情况下，拟合曲线也十分光滑。不足之处就是不能展现出小尺度的变化。解决方法就是以ZDR、ZH和KDP三个极化变量构建的物理约束，通过ZDR和ZH两个极化变量反演出具有较好精细尺度的KDP。

虽然基于KDP的降水估计算法R(KDP)相较于R(ZH)更少地受雨滴谱影响，但是对于较小的降雨率，当ZH在20～30 dBZ时，基于KDP计算的降雨率估计并不理想[4-5]。Chen等[6-8]针对不同的水凝物采用不同的关系式。Zhang等[9]针对不同的KDP的值选取不同的降水估计方法进行定量降水估计，获得比较好的结果，本文中采用该方法进行降水估计。

2 基于物理约束的变分方法

2.1 质量控制

质量控制算法可以有效地剔除非气象回波的数据和地物杂波。其中由于地物杂波和异常传播造成高ZH值可以通过异常值检测的方法消除，但是由飞禽类等生物目标造成的低ZH值很难被消除。首先剔除信噪较小（SNR<20 dB）的观测值[10]。Valliappa Lakshmanan(2014)[11]提出了一种天气雷达的极化变量的质量控制方法，其主要是对水平反射率因子(ZH)、极化相关系数(ρHV)和差分反射率因子(ZDR)三个变量进行阈值控制，具体方法为：

对ZH在径向上使用1 km的滑动窗口进行滑动平均，对ZDR和ρHV在径向上使用2 km的滑动窗口。对于ΦDP的质量将在边界条件部分详细描述。由于本文应用的变分法对纯降水估测有效，因此选取融化层以下的数据。以0.5°仰角为例，选取150 km以内的数据，最大高度约为1.3 km，根据一些华南降水的研究[12-13]，可以确保所选择的数据在融化层高度以下。

2.2 物理约束

Scarchilli等[14]研究了水平反射率因子，差分反射率因子和比差分传播相移三者之间的关系，确定了三者之间的物理约束，即可以通过任意ZDR和ZH两个极化变量通过物理约束计算出KDP。三者之间的关系式如（5）式所示。

其中，ZH的单位是mm6/m3，ZDR的单位是dB，由ZH和ZDR两个变量估计得到,φi为根据物理约束得到的反演得到的差分相位，φ0为径向上的初始差分相位，本文中将近边界条件作为初始差分相位，具体计算过程在2.3节。Scarchilli等[14]使用大量S波段的观测数据进行拟合，得到了公式（5）的经验参数，其 中C=1.05×10-4、α=0.96、β=0.26。本文基于Scarchilli给出的经验参数，结合本地观测数据给出了本地化参数，其中C=1.37×10-4、α=0.88、β=0.20。通过公式（5）和（6）可以通过估计的KDP,进而对ΦDP进行重构。两组经验参数组合实际应用情况如图1所示，本地化参数可以很好反映出观测数据的趋势。

图1中的黑色星点为一条ΦDP径向观测数据,红色实线是基于Scarchilli给出的经验参数进行的ΦDP的重构，蓝色实线是基于本地化参数进行的ΦDP的重构。基于经验参数重构的ΦDP整体上高于观测数据，而基于本地化参数重构的ΦDP位于观测数据之间，较好地拟合出观测数据的大致走势。

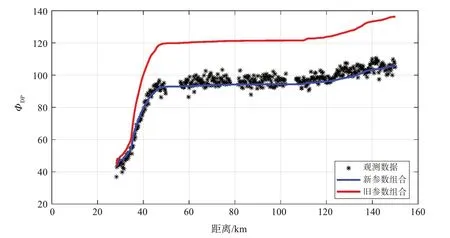
图1 基于物理约束的ΦDP重构

在经过异常值检测并剔除后，ΦDP径向观测数据可能会变得不连续，因此需基于物理约束重构的ΦDP对径向观测数据的缺失值进行填补。

2.3 边界条件

变分方法需要计算近端和远端的边界条件Φnear和Φfar，以保证重构的ΦDP在两个边界条件之间。由于Maesaka(2012)计算边界条件的步骤较为简单，对异常数据的影响较敏感，且计算边界条件需选取连续20个有效样本进行边界条件的计算，信息损失较大。基于上述缺陷，我们进行了一定的修正，在尽可能保留足够多信息的情况下，使边界条件的计算更加稳健。首先对ΦDP观测数据进行质量控制，以一条径向数据为例，在剔除ρHV<0.9的数据之后，通过遍历所有数据计算连续数组的切片索引。之后对索引进行如下处理。(1)若两索引之间间隔小于5，且前一个索引最后的数据和后一个索引的首个数据相差小于30°，将两个索引合并为一个索引。(2)若索引内的数据个数小于3个，将被视为孤立数据被删除。(3)遍历所有数据如果某个距离库的ΦDP的值与相邻的数据差值大于35°，则将该数据视为被杂波污染的数据并使用两个相邻数据的平均值进行替换。进行质量控制示意图如图2所示。橙色的距离库表示缺失值，红色的距离库表示异常值径向数据（a）有两个连续数组的切片索引，分别为（1，6）和（10，16），这两个索引对应的距离库间隔为3，小于5，则将两个索引合并为一个索引，即（1，16）。径向数据（b）有两个连续数组的切片索引，分别为（4，5）和（11，11），这两个索引对应的距离库长度均小于3，因此视为孤立点并删除。径向数据（c）有一个异常值，即 |φDP7-φDP8|>35°, |φDP6-φDP7|>35°，因此视为被杂波污染的数据并使用相邻的距离库的平均值进行替换。

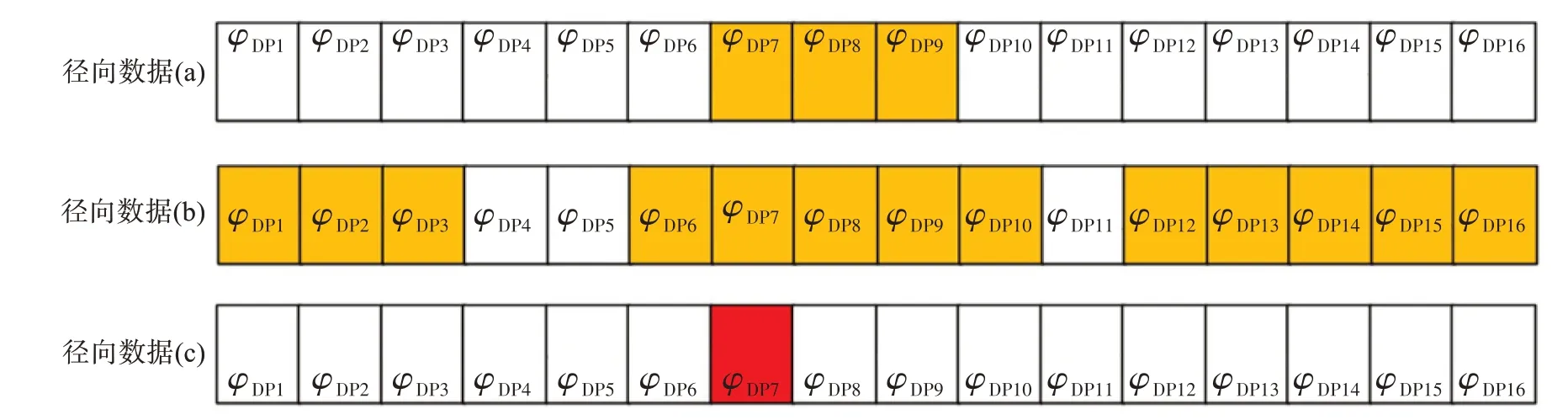
图2 ΦDP观测数据质量控制示意图

然后计算近边界条件Φnear，步骤如下。

(1)从头到尾遍历径向数据的索引，若索引所代表的数组元素大于20个，则该数组前20个数据作为近边界条件计算的样本。

(2)计算选取的样本(X1,X2,……,X20)与对应距离(r1,r2,……,r20)的线性回归的斜率K。

(3)如果K>0，则近端边界条件Φnear为最近距离r1的预测值，否则，近端边界条件为所取样本的中位数。

近边界条件可以等效视为系统初始差分相位φ0，在计算完近边界条件之后，可以使用物理约束重构ΦDP，然后对径向数据中的缺失值进行填补。远端边界条件Φfar的计算方法与近端边界条件相似。

(1)从尾到头遍历径向数据的索引，若索引所代表的数组元素大于20个，则该数组后20个数据作为远边界条件计算的样本。

(2)计算选取的样本(Xend-19,Xend-18,……,Xend)与对应距离(rend-19,rend-18,……,rend)的线性回归的斜率K。

(3)如果K>0，则远端边界条件Φfar为最远距离rend的预测值，否则，远端边界条件为所取样本的中位数。

图3为远-近边界条件计算方法的示意图，近边界条件为选取最近的20个有效样本点进行线性拟合，远边界条件为选取最远的20个有效样本点进行线性拟合，远近边界条件受到噪声的影响较小，在本文中，将近边界条件视为该径向方向上的初始相位ϕ0，初始相位可以在填补数据起到作用。

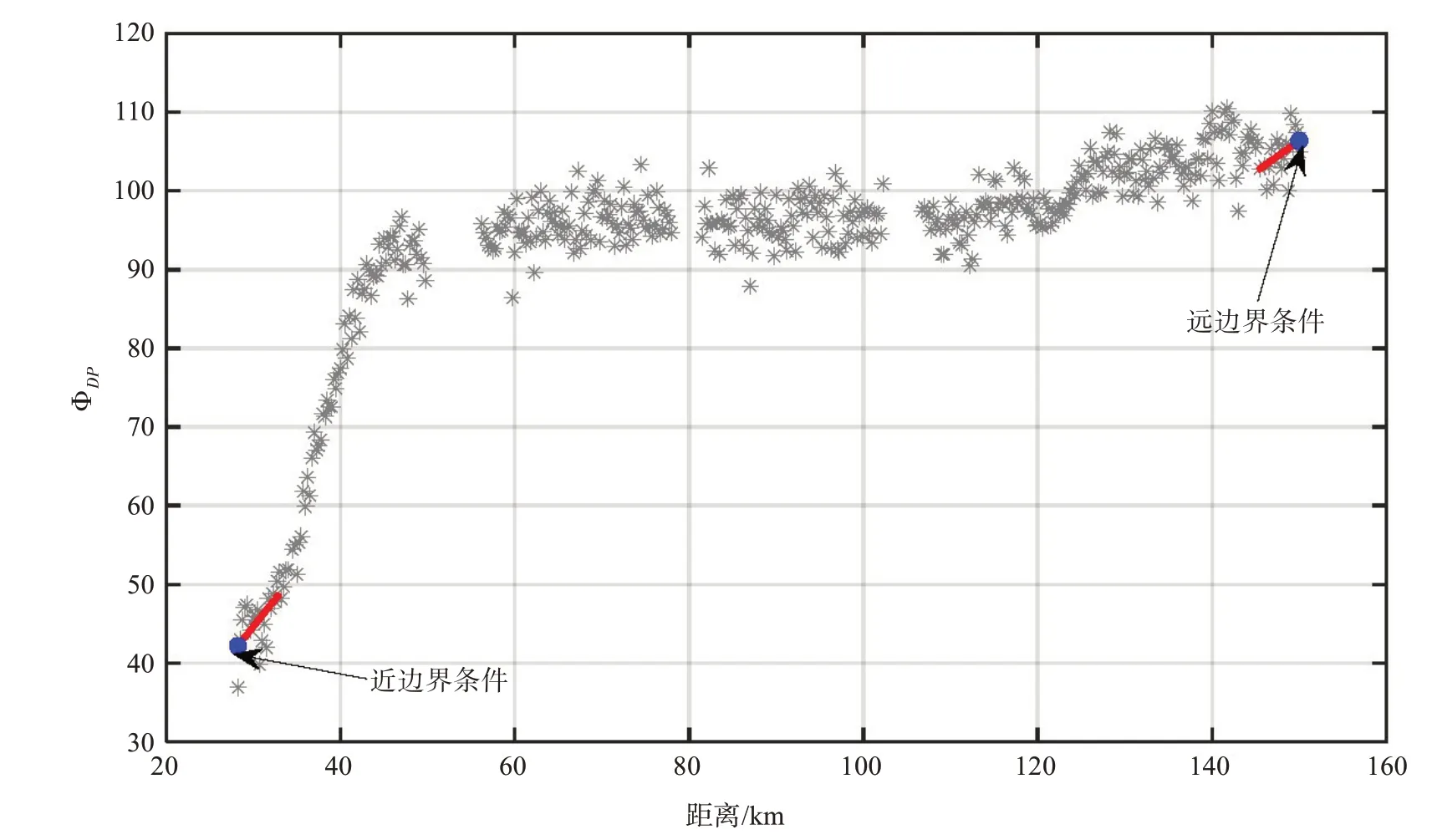
图3 边界条件计算

2.4 代价函数

在构造代价函数之前，需要构造几个中间变量，对于一条有N个距离库的雷达径向观测数据，本文定义差分相位观测值(ΦDP)i，理论的差分 相 位为(ϕDP)i，比差分传播相移(KDP)i，其中i=1,2,……,N。

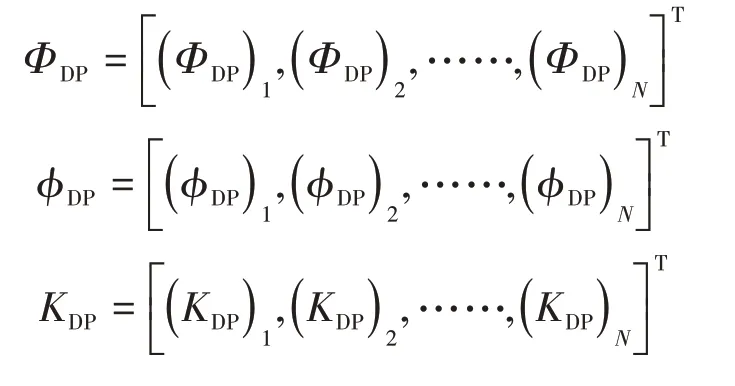
然后给出的φ的定义：

根据（1）式中所给出的K DP的定义，这里引入一个前向算子H1，φ可以表示为：

其中∆r是雷达距离分辨率。因为ΦDP是递增的，KDP是非负的，为了保证KDP非负，引入了k2，其表示如下：

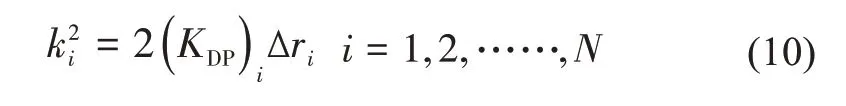
然后将式（10）带入式（9），φ的表达式可以写为：

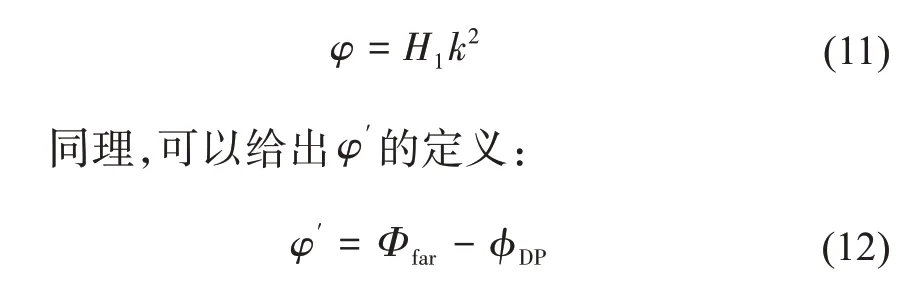
通过引入后项算子H2,φ'可以写成与式（11）相同的形式：

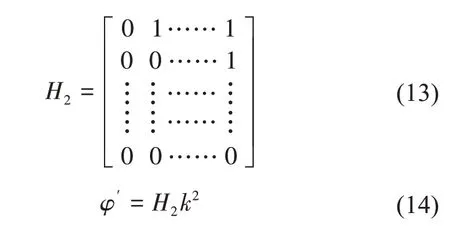
观测的差分相位与边界条件的差值为：

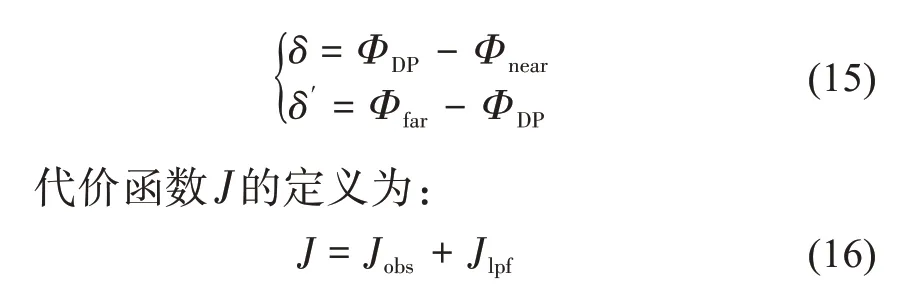
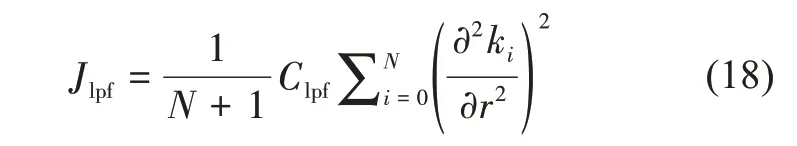
Jobs项是观测项和重构的理论项的均方误差，是代价函数中的主要部分，使重构的差分相位更好地拟合观测的差分相位。Jlpf是参数k的拉普拉斯算子，相当于一个低通滤波器，Clpf是滤波器的参数，一般取值较大。将当代价函数取最小值时的k作为最终的解，然后通过k计算KDP，本文选取的迭代方法为拟牛顿法，该方法需要代价函数的偏导数作为迭代方向。代价函数关于k的偏导数如下所示：

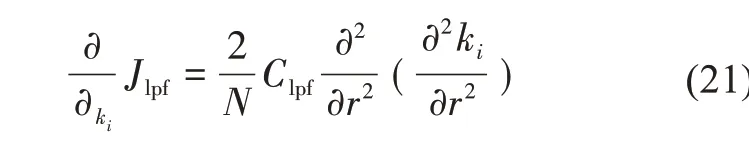
通过代价函数和关于k的偏导数，使用牛顿迭代法进行求解，最终重构ΦDP[15]。

图4为变分方法拟合和物理约束的效果图，其中黑实线为径向数据观测值ΦDP，蓝实线为变分拟合的ϕDP，红实线为变分拟合的KDP，紫色实线为物理约束KDP，绿色实线为物理约束基于物理约束KDP得到的ϕD（P简称物理约束ϕDP）。从图中可以看出变分拟合的ϕDP可以很好地反映出观测值ΦDP的趋势，并且消除了大部分的随机误差，物理约束KDP在30 km处有一个较大的异常值，相比于物理约束KDP，变分拟合KDP表现得更加平滑，且符合实际情况。

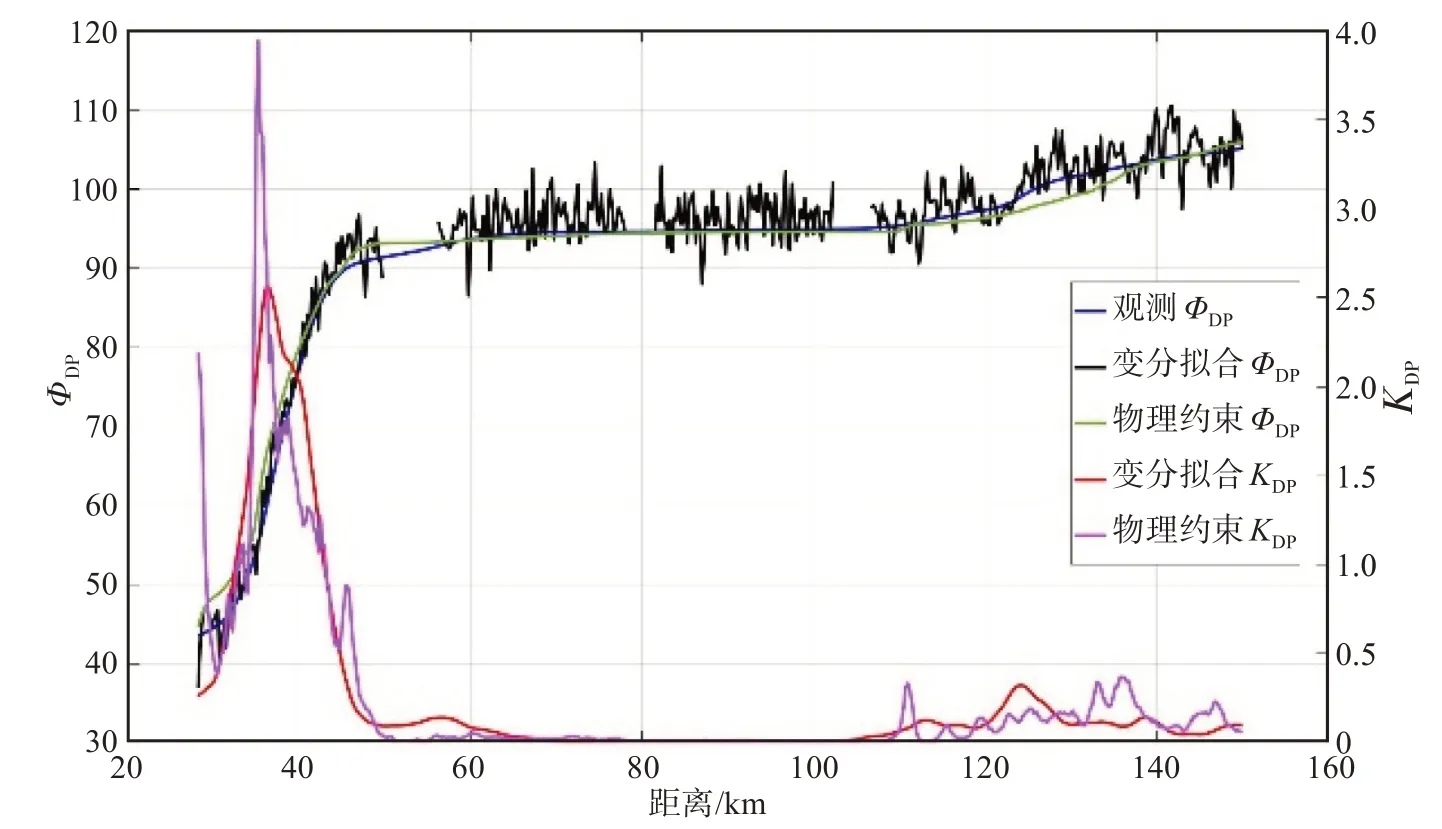
图4 变分拟合结果

2016年5月7日06点54分0.5°仰角ϕDP、KDP的扫描数据图如图2a~2b所示，经过质控和填补后的结果如图5c~5d所示。在ϕDP、KDP的原始数据里存在局部范围的缺失值，如雷达的东北方向和西北方向，在经过质量控制和物理约束的填补后数据在空间变得连续，过滤掉大部分的噪声，并且保留了主要的回波部分。图5e~5f是经过2.4节所描述的变分方法拟合后的数据图像，可以看出经过变分拟合后，ϕDP和KDP的数据在空间上变得光滑，可以更好地反映出雷达KDP的数据。

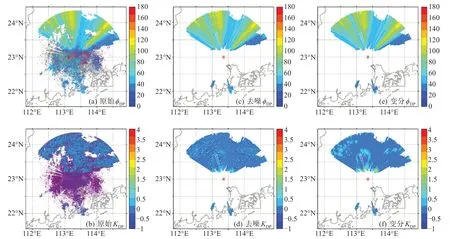
图5 2016年5月7日06点54分0.5°仰角ϕDP、K DP的数据图

3 实证分析

3.1 数据与降水估计方法

本文选取广东省2 400多个雨量站作为地面实际观测数据，主要研究2017年5月7日00—24时的降水事件，当天最大累计降水超过300 mm。雷达数据选取广东省广州市的一个S波段的极化雷达。

KDP对小雨滴的降水估计效果较差[8]。Zhang等[9]运用了一种组合降水估计方法（RQPE），该方法使用ZH、ZDR和KDP三个极化变量进行估测，并给出了基于2014年4月—2015年5月的位于广东省西南部的2DVD观测到的雨滴谱数据拟合的经验公式，经验公式如下所示：

其中，ZH(mm6/m3)是水平反射率因子，ZDRl=10ZDR/10是线性尺度上的差分反射率因子。本文使用经过变分重构后的KDP数据，基于Zhang等[9]的RQPE方法和经验公式进行降水估计，整个算法（V-RQPE）的流程图如图6所示。其中，T1=38 dBZ，T2=0.5 dB，T3=0.1°/km。

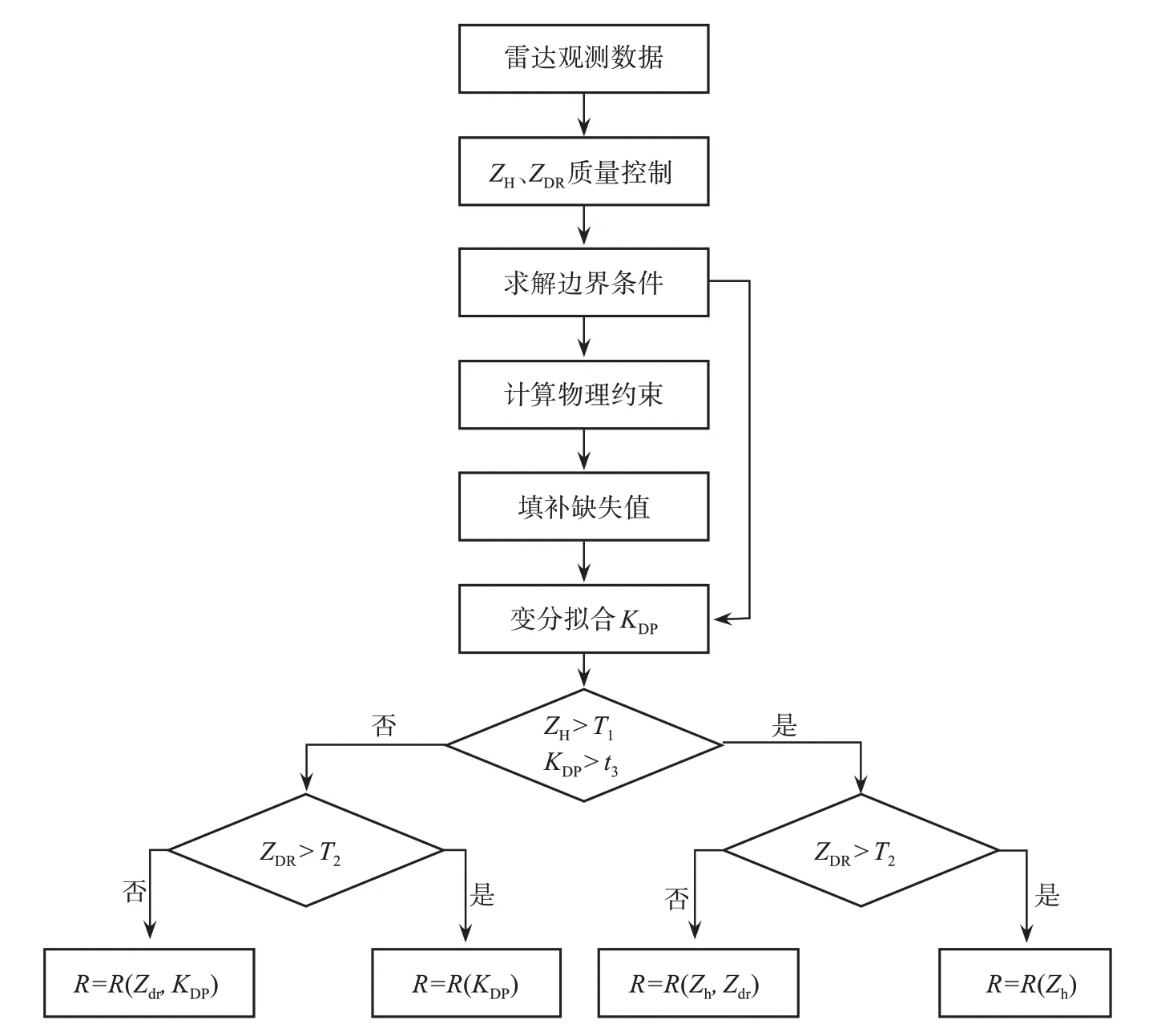
图6 V-RQPE算法流程图

首先用克里金插值方法（KRIG）将雨量站插值到0.1°×0.1°的网格场上，获得逐小时的降水产品，同时将基于V-RQPE估测的降水量也进行重采样转换到0.1°×0.1°的网格场上，以方便比较降雨事件的空间分布。图7为基于KRIG插值、VRQPE的24小时累计降水估测值图像，V-RQPE在雷达中心位置可以很好估计出降水量，但是在雷达的北部估测效果与实际值相比偏低。

图7 24小时累计降水观测值与估测值

3.2 评估指标

在该部分，本文选取了2017年5月7号广州市00—24时的降水过程进行试验，其中最大的降水量超过100 mm/h。在评估过程中，采用相关系数（CC）、均方误差（RMSE）、相对偏置（RB）和分数均方差（FRMSE）四个评估标准来评估该变分方法的性能：

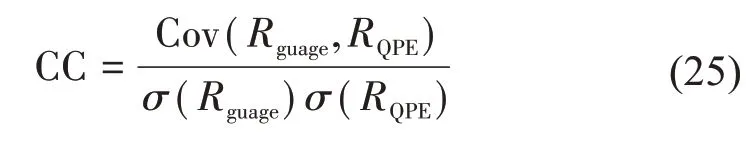
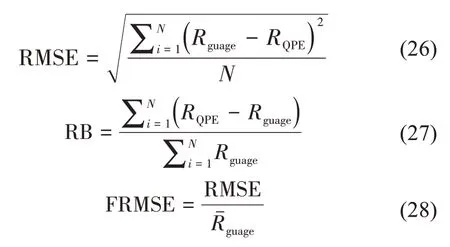
公式(25)~(28)分别是相关系数（CC）、均方误差（RMSE）和相对偏置（RB）的计算公式，其中Rguage表示雨量站的观测值，guage为Rguage的对应0.1°×0.1°的网格点的空间平均值，RQPE为估测的降雨率，QPE为RQPE的平均值。相关系数（CC）表示QPE估测值和实际观测值的相关关系，相关关系越大，估测效果越好。均方误差（RMSE）表示观测值与QPE估测值的差距，RMSE越大，QPE的估测效果越差。相对偏置（RB）表示QPE估测值与观测值的相对误差的程度，如果大于0则表示降雨率被高估，小于0则表示降雨率被低估。分数均方差（FRSME）为均方误差（RMSE）与观测值均值之比，是一个无量纲的统计量，在针对不同量级的降水事件时，可以更好评估估测误差。

3.3 累计降水估测效果

本文使用2017年5月7日00—24时的广州雷达第一仰角（0.5°）观测数据，图5a~5b为06点54分0.5°仰角ϕDP、KDP的PPI扫描图像。经过质量控制之后，使用基于物理约束的变分方法，对ΦDP进行变分拟合，然后利用3.1节所描述的RQPE算法进行降水估计，24小时累计降水估计如图7b所示。之后将雨量站进行重采样转换到0.1°×0.1°的网格场上的数据与RQPE算法估计的降水量数据绘制成散点图，并计算相应的评估指标，图8分别为1、3、6、24小时累计降水的散点图，其色标为散点相对密度，红色相对密度最大，蓝色最小。

图8 累计降水散点图

从图8中可以看出，对于不同时长的累计降水估计，RQPE的性能表现也有所差异。一般来说，随着时长的增加，相关系数会略微增大（CC从0.778到0.838），均方误差也会增大（RMSE从4.06到23.73），但是分数均方差（FRMSE）却有一个起伏的过程，从不同时间的累积降水对比图可以看出，小降雨量存在高估的现象，大降雨量存在低估的现象，产生这种误差的可能是雷达数据和雨量站数据的质量，RQPE算法中的不确定性造成的。

3.4 多种QPE方法比较

为了比较基于变分拟合的降水估计方法的性能，本文采用了六种不同的降水估计方案进行对比，具体方案如表1所示。

表1 六种QPE方案配置表

表1显示了六种不同的降水方案的配置，分别V-RQPE采用本文的变分拟合方法，使用RQPE的方法进行降水估计；RQPE采用Zhang等[9]的质控方法进行降水估计；R-Z采用公式（21）进行降水估计；R-Z-ZDR采用公式（23）进行降水估计；RVKDP采用公式（22），基于变分拟合的KDP数据进行降水估计；R-OKDP采用公式（22），基于滑动平均和物理约束填补的KDP数据进行降水估计。图9为上述六种QPE算法一小时累计降水估计的散点图。

从图9可以看出各种QPE方法的差异比较明显，除了R-OKDP方法外，其他五个QPE方法的相关系数均较高（CC>0.7）。两个组合算法V-RQPE和RQPE中，V-RQPE的CC（0.77）、RMSE(4.06)和FRMSE（2.769）相对较小，但是存在低估的现象。从图9b中看出，虽然RQPE的RB绝对值较小，但是对小降雨量存在高估现象，大降雨量存在低估的现象。其他四个单一算法里R-Z的相关系数最高(0.841)，但其低估严重（-72.77%），估测效果较差。R-Z-ZDR算法也拥有较高的相关系数（0.801 1），但是其在降雨率较大时估计误差明显增大。R-VKDP和R-OKDP两个算法相比，但是R-VKDP拥有更好的统计性能。就单一算法而言，R-VKDP估测效果较好。

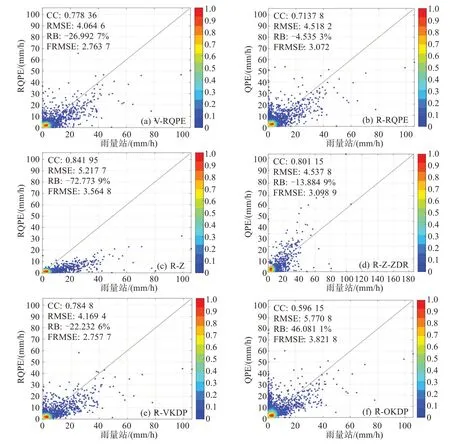
图9 六种QPE方法的1小时累计降水估计对比

表2为6种QPE方法计算的24小时累计降水的评估结果。与1小时累计降水估计相比，24小时累计降水的RMSE均有不同程度的增大，24小时累计降水由于误差累积，可能出现误差抵消，所以六种方法的相关系数都有一定升高。就四个评估指标而言，V-RQPE和R-VKDP的估测效果是最好的，RQPE次之，R-OKDP估测效果最差。

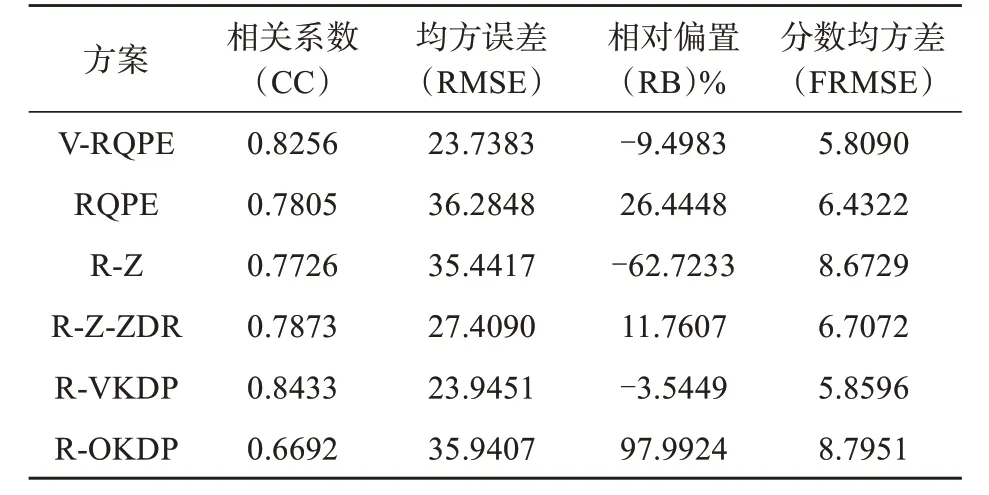
表2 六种QPE方法24小时累计降水估计评估表

4 结 论

本文将物理约束应用到ΦDP观测值的缺失填补中，使用了更加稳健的方法求解边界条件，这种方法可以在稳健地求解远近边界条件的同时，保留更多的原始信息。之后使用变分方法重构ΦDP，进而反演出非负的KDP，并将其应用到定量降水估计中。以2017年5月7日的广州S波段雷达的回波数据为例，使用了Zhang等[9]的RQPE方法进行降水估计，并使用了其他五种不同的方法进行对比，采用相关系数、均方误差、均方误差、分数均方差等指标进行评估，验证了基于变分方法的降水估计的性能。

（1）变分拟合的ϕDP保留了观测值ΦDP的大多数的信息，并消除了随机误差。对于24小时累计降水，RQPE算法可以较准确地估计降水中心的降水。不同时长的累计降水估计性能表现不同，但存在一定低估的现象。

（2）对于六种不同的降水估计算法，在1小时累计降水估计的评估中，V-RQPE拥有较高的相关系数（CC=0.77），较低的估计误差（RMSE=4.06，FRMSE=2.76）；R-Z相关系数最高（CC=0.84），但其低估严重（RB=-72%），估计误差也较大；R-ZZDR在降雨率大估计误差会变大；R-VKDP和RSKDP估计性能相似，但是R-SKDP会出现负的降雨率；R-OKDP表现最差。在24小时累计降水估计的评估中，随着时间的增加，降水量也会增加，RMSE在增加，但是无量纲的FRMSE在减小。六种QPE方法中，V-RQPE和R-VKDP的评估指标是最好的，拥有较高的相关系数、较低的估测误差。

本文所设计的变分方法可以很好消除KDP的误差，不论实在组合算法中还是单一算法中，都可以有效地降低定量降水估计中的不确定性，但是依然存在一定的低估现象，可能是由于雷达数据和雨量站数据的质量，RQPE算法中的不确定性造成的，也可能是由于平滑滤波器的选择问题，虽然最大限度地减少了随机误差，但可能会使KDP变小导致低估。消除误差会伴随着损失信息，两者如何才能达到均衡，是本文以后的主要研究方向。