多刚体动力学仿真的李群变分积分算法*

黄子恒 陈菊† 张志娟 田强

（1.北京理工大学 宇航学院力学系，北京 100081）（2.北京空间飞行器总体设计部，北京 100094）

引言

常用多刚体系统动力学建模方法有自然坐标方法[1]、欧拉角方法[2]、欧拉四元数方法[3]、李群李代数方法[4]等.自然坐标方法通过若干刚体上的基点以及若干内嵌在刚体上的单位向量表示刚体位姿，采用该方法可以得到含常数质量矩阵的多刚体系统动力学方程.其余常规动力学建模方法则通过刚体质心坐标与刚体的姿态来确定刚体的位姿，以姿态的不同表示方法进行区别.常用的姿态表示方法有欧拉角[2]、欧拉四元数[3]、李群SO（3）矩阵[4]等.欧拉角方法是常用描述刚体姿态的方法，计算简便.描述刚体在三维空间中的运动姿态可采用2类12种欧拉角系统，但无论采用哪种欧拉角系统，都不可避免会含有奇异点[5].欧拉四元数方法用4个有约束关系的参数描述刚体姿态，避免了奇异问题[5].然而，欧拉四元数方法的表述并不直观，内蕴约束方程会影响动力学方程的求解效率，其双值性甚至会导致刚体系统控制中的退绕现象[6].李群方法则采取指数映射进行迭代，使得刚体姿态旋转矩阵始终保持为正交矩阵.李群SO（3）对应的李代数空间so（3）同构于三维欧氏空间R3，因此李代数空间的元素由3个独立的坐标构成.在每一步迭代的过程中李群方法无需考虑多个参数之间的约束关系，有助于提高计算效率.

刚体的动力学应具备守恒性质，如保守系统的能量守恒，动量守恒等.为不与物理规律相悖，守恒律已经成为检验动力学建模与数值算法的重要标准.虽然用李群方法建模的性质优越，但由于李群自身的非线性性质，使得欧氏空间上的常规数值算法在求解多刚体动力学方程时失效，如常规的Runge-Kutta方法不仅无法保证首次积分守恒，还会产生较大的能量耗散与结构误差[7].目前主要用如下两种方法改进已有李群算法的不足：

方法一、采用新数值离散格式离散系统连续动力学方程.该方法通过引入李括号项可使系统的位形空间始终在真实的李群空间中迭代.例如，Munthe-Kaas基于经典Runge-Kutta算法，通过引入校正函数[7，8]提出了一种 Runge-Kutta-Munthe-Kaas（RKMK）算法.该算法能保证迭代过程在系统正确的微分流形上进行.Wieloch与Arnold[9]将BDF方法与李群方法相结合提出了BLieDF方法，在尽可能不丢失精度的同时使用更少的李括号项，提高了计算效率 .Brüls[3，10]基于两种描述刚体位形的李群（SE（3）与ℝ3× SO（3）），结合广义α方法提出了Lie-广义α方法.Lie-广义α方法已被成功应用于多种多体动力学建模与计算，例如：空间曲柄滑块[11]，柔性四杆机构[12]以及空间捕获飞网[13]等 .李亚男等[14]使用Lie-广义α方法求解指标为1的微分代数方程，使仿真过程中能够同时保持位移约束、速度约束与加速度约束，提高了计算精度.

方法二、李群变分积分算法[15].该算法采用离散Hamilton变分原理建立系统的动力学方程，获得系统的非线性方程组并求解，具有理想的保辛、保动量、保能量等性质.已有研究已构造了多种Hamilton变分过程中Lagrange量的多种离散格式，提出了相应的李代数离散格式下的李群变分积分算法.李群变分积分算法充分结合李群李代数方法与变分积分算法的优势，相较常规变分积分算法不仅能够直接减少参数之间的约束方程，显著提高计算效率，还能保持系统几何结构，提高计算精度.本文将基于差分方法推导的李群变分积分公式称为一般格式李群变分积分公式.一般格式李群变分积分算法已经被应用于空间双连杆机械臂[16]、无人潜艇[17]、无人机编队[18]、轨道控制[19，20]等动力学建模与控制研究中，在解决这些实际问题时表现出了保持系统能量与结构的特性.

进一步，Hante 和 Arnold[21]通过对数映射改进了以上一般格式算法中的李代数元素离散方式得到RATTLie变分积分算法.该算法在Cosserat柔性梁动力学分析中表现出较好的能量守恒特性.史东华和Zenkov[22]通过直接对李代数元素进行变分的方式提出了Hamel场变分积分算法.该方法已被应用于抓取机械臂[23]、柔性梁[24]等多体动力学与控制研究，展现出了较好的数值特性.Hall和Leok[25]提出了李群谱变分积分算法，重力作用下的单摆动力学算例研究表明：采用大积分步长，该方法同样能长时间保持系统能量与数值稳定.随着多自由度复杂约束动力学问题的出现，白龙等[26]通过Kelly变换与Newton迭代克服了李群变分积分算法的隐式求解问题，提高了计算效率.Lee等[27]提出了多体系统的线性变分积分器，通过离散递归牛顿欧拉算法（Discrete recursive Newton-Euler algorithm）求解残差向量，以及铰接体惯性算法（Articulated body inertia algorithm）计算更新迭代值，提高了计算效率.

本文基于李群李代数的离散Hamilton方程，建立了Hamilton体系下多刚体系统动力学两类李群变分积分算法.分别采用三种算法（一般格式的李群变分积分算法、RATTLie变分积分算法与Lie-广义α算法）计算了重力作用下空间刚体双摆的动力学问题，对比研究了各算法的能量误差、约束违约等特性.研究表明一般格式的李群变分积分算法与RATTLie变分积分算法在长时间保持系统结构、能量等方面存在显著优势，具有潜在工程应用前景，如：航天器轨道动力学问题、大型柔性空间结构在轨服务操作动力学问题等.

1 离散Hamilton体系下的李群变分积分算法

李群变分积分公式是通过离散的Hamilton变分原理得到的动力学方程组，而非对连续的动力学方程组直接进行离散.本文用G表示李群，用g表示李代数，用g*表示李代数的对偶空间.

2 多刚体系统动力学方程的两种离散格式

2.1 一般离散格式

图1 多刚体系统构形示意图Fig.1 Schematic view of a multi-rigid body system configuration

2.2 RATTLie离散格式

3 数值计算与分析

考察如图2所示的重力作用下的空间刚体双摆动力学特性.两根摆均为圆柱刚杆，杆1（OA）与杆2（AB）的质心为O1，O2，两根相同杆的基本参数为：密度ρ=7850kg⋅m-3，底部半径为r=0.05m，母线长为l=1m.杆1与杆2质量为m1=m2=61.6538kg，杆1与杆2的惯性张量矩阵为初始时刻t0=0时空间双摆模型状态如图2虚线所示，杆1一端球铰约束在固定点O，杆1与杆2由A处球铰连接.初始时两摆呈垂直关系，杆1的位形由位姿矩阵R1，0=I3×3与质心坐标x1，0=[0 0.5 0]T确定，杆2的位形由位姿矩阵与质心坐标x2，0=[-0.5 1 0]T确定 .初始杆 1 与杆 2的体角速度Ω1，0=Ω2，0=[0 0 0]T，初始杆1与杆2的质心平动速度1，0=2，0=[0 0 0]T.

图2 重力作用下的空间双摆模型示意图Fig.2 Schematic view of a spatial double pendulum under the gravity action

杆1的局部坐标系O1-X1Y1Z1与杆2的局部坐标系O2-X2Y2Z2如图2所示，两杆运动过程中只考虑重力影响，设经过时间tn后杆1可到达OA′处，杆2可到达A′B′处.

双摆系统有两处约束，O处球铰为约束1，A处球铰为约束2，综合写为

式（24）中的Xij为约束j处的球铰到摆i的质心的位置向量，本算例中X11=[0 -0.5 0]T，X12=[0 0.5 0]T，X21=[0 -0.5 0]T.表1给出了双摆对应的约束Jacobi矩阵表达.

表1 空间双摆的约束Jacobi矩阵Table 1 Jacobi matrix of the double pendulum’s constraints

采用Lie-广义α方法计算时，算法谱半径选取为0.9.另外两类Hamilton体系变分积分算法则直接求解非线性方程组.Lie-广义α方法，一般格式的李群变分积分算法与RATTLie变分积分算法均使用10-3步长进行计算.采用商业软件Recurdyn分别使用10-4、10-5两种步长进行计算.用“Lie-alpha”表示Lie-广义α方法，“DH”表示一般格式的李群变分积分算法，“RL”表示RATTLie变分积分算法.仿真总时间设为50s，使用Matlab进行编程，在一台具有Intel Core i7-7700 3.6GHz处理器及16GB RAM的PC机上运行.

图3为以上所有方法摆2的质心O2点位移矢量的X轴方向分量结果，图4为以上所有方法杆2的角速度矢量绕O2X2轴方向的分量结果.根据图3与图4可知：当步长为10-4时，商业软件Recurdyn在4s以后计算结果逐渐发散；当步长为10-5s时，Lie-广义α方法与李群变分积分算法（DH，RL）的所得结果与商业软件Recurdyn计算结果几乎重合，说明了本文建立的建模与计算方法的正确性.

图3 杆2质心O2点位移矢量的X轴方向分量Fig.3 X-component of the second pendulum’s mass center O2

图4 杆2角速度矢量绕O2X2轴方向分量Fig.4 Component of the second pendulum’s angular velocity about axis-O2X2

图5为DH方法、RL方法与Lie-广义α方法的能量波动情况对比图，其中图5（b）为图3（a）在7.5～10s的放大图.由图5可知：1、Lie-广义α方法的能量波动远远大于李群变分积分算法.2、当步长选取为10-3时，DH方法已经远远优于步长为10-4的商业软件方法，可知DH方法在计算过程中耗散极低基本保持稳定.3、RL方法在能量保持方面优于DH方法，可知数值离散的高精度格式可以提高计算精度.

图5 空间双摆的能量变化曲线对比图：（a）0～50s（b）7.5～10sFig.5 Comparison of the spatial double pendulum’s energy variations ：（a）0～50s（b）7.5～10s

图6为Lie-广义α方法，DH方法，RL方法的SO（3）正交性误差曲线对比图.SO（3）群元素R需要满足正交性条件，而‖I3×3-RRT‖表示SO（3）群元素R的正交性误差，可以反映算法迭代过程中的群结构保持情况.从图6中明显可以看出，三种方法的正交性误差保持量级均在10-14，算法使得系统的李群结构保持很好.

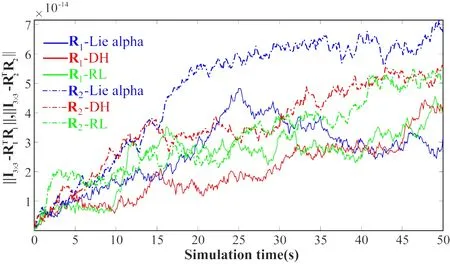
图6 空间双摆SO（3）正交性误差曲线对比图Fig.6 Comparison of the spatial double pendulum’s SO（3）orthogonality error curves

图7给出了DH方法与离散Euler-Lagrange方程建模方法（DL方法）、Lie-广义α方法的A处球铰的速度约束误差对比曲线.从图7可以看出，由于Lie-广义α方法与离散Euler-Lagrange方程组[14]并未对速度进行违约校正，速度误差的量级已经达到10-4.DH方法引入速度约束方程后速度误差量级为1e-16，显著改善了约束违约情况.引入速度约束方程后，基于Hamilton体系的RATTLie算法对系统约束保持情况也将显著改善.

图7 空间双摆速度约束违约曲线对比图Fig.7 Comparison of the spatial double pendulum’s velocity constraint violation curves

4 结论

基于离散变分原理建立了多刚体动力学模型的一般格式李群变分积分算法和RATTLie变分积分算法.通过算例对比分析发现：一般格式的李群变分积分算法和RATTLie变分积分算法具有保能量、保结构的性质.在积分步长选取较大时，该方法远远优于步长较小的商业软件的计算结果；RATTLie方法的系统能量保持特性优于一般格式算法；采用Hamilton体系的李群变分积分算法相比离散Lagrange体系的算法能量波动范围更小，约束违约更小.后续可进一步研究这类算法的并行计算问题以及基于这类算法的多柔体动力学与控制问题，特别是在轨大型柔性空间结构的组装过程动力学与控制问题.