全直线上四阶方程的Laguerre-Legendre-Laguerre复合谱逼近①
2022-08-24叶小华庄清渠
叶小华, 庄清渠
(1.黎明职业大学通识教育学院,福建 泉州 362000;2.华侨大学数学科学学院,福建 泉州 362021)
0 引 言
谱方法因具有高精度的优点,已成为求解微分方程数值解的重要方法之一[1,2].谱方法在无界区域问题上的应用也越来越广泛,如对区域进行截断,引入适当的人工边界条件,再用谱方法进行数值求解;通过区域映射把无界区域问题转换为有界区域问题,用有界区域上的谱方法进行求解;直接采用定义在无界区域上的正交多项式(函数)进行求解,关于这方面的详细介绍可见综述性文献[3,4].利用谱方法求解无界区域上的四阶方程也有一些研究工作,文献[6]研究了半直线上四阶方程的Legendre-Laguerre耦合谱逼近;文献[5]研究了一维半无界区域四阶方程的Legendre-Laguerre耦合谱元计算;文献[7]则研究了半无界条状区域四阶方程的Laguerre-Legendre混合谱逼近;文献[8,9]分别研究了全直线区域上的对角化Legendre有理谱方法以及对角化Chebyshev有理谱方法.文献[10]研究了全直线上四阶方程的Laguerre-Laguerre复合谱逼近,数值结果说明方法对求解具有衰减缓慢解析解的问题具有优越性.将进一步研究发展Laguerre-Legendre-Laguerre(Lag-Leg-Lag)复合谱方法求解全直线上的四阶方程,通过数值算例说明方法的谱精度.
1 问题及变分形式
记I=(-∞,∞),考虑如下的四阶问题,如式(1):
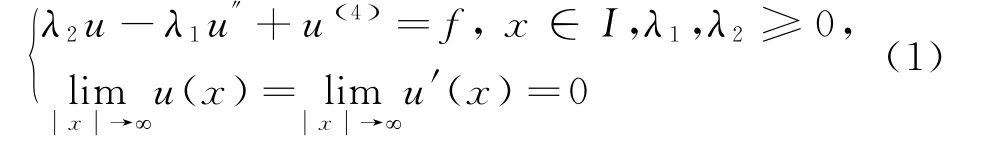
接下来将对问题(1)用Lag-Leg-Lag复合谱方法进行求解.为此,首先对区域进行剖分.首先 将(-∞,∞)剖 分 成(-∞,a1],[a1,a2],[a2,∞)三部分,然后在三个区间上分别采用Laguerre谱方法,Legendre谱方法,以及Laguerre谱方法进行逼近.为了叙述方便,不妨设a1=-1,a2=1,并记I0:=(-∞,-1],I1:=[-1,1],I2:=[1,∞),u Ik:=u Ik,k=0,1,2.此外,记N=(M0,M1,M2),并令P M1(I1)表示I1上次数不超过M1的全体多项式组成的空间.另外记
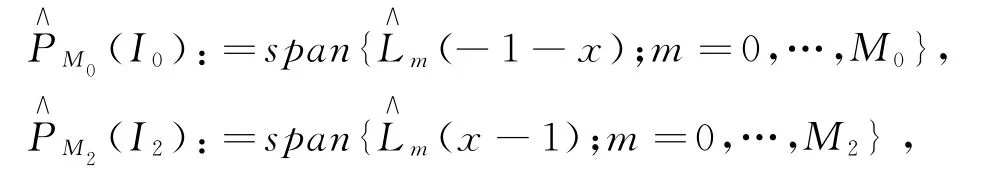
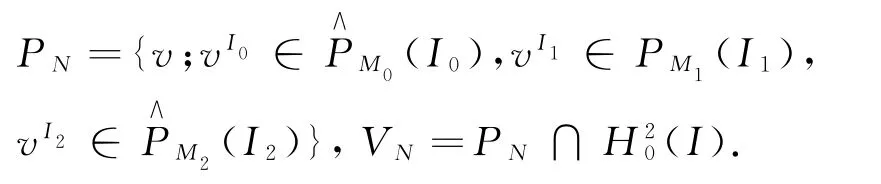
此时,问题(1)的Lag-Leg-Lag复合逼近形式为:找u N∈V N,如式(2):
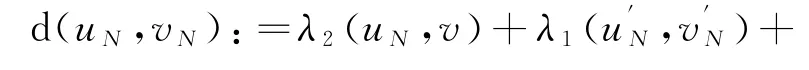
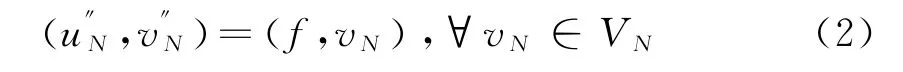
2 计算实施
详细介绍如何对逼近问题(2)进行离散计算.
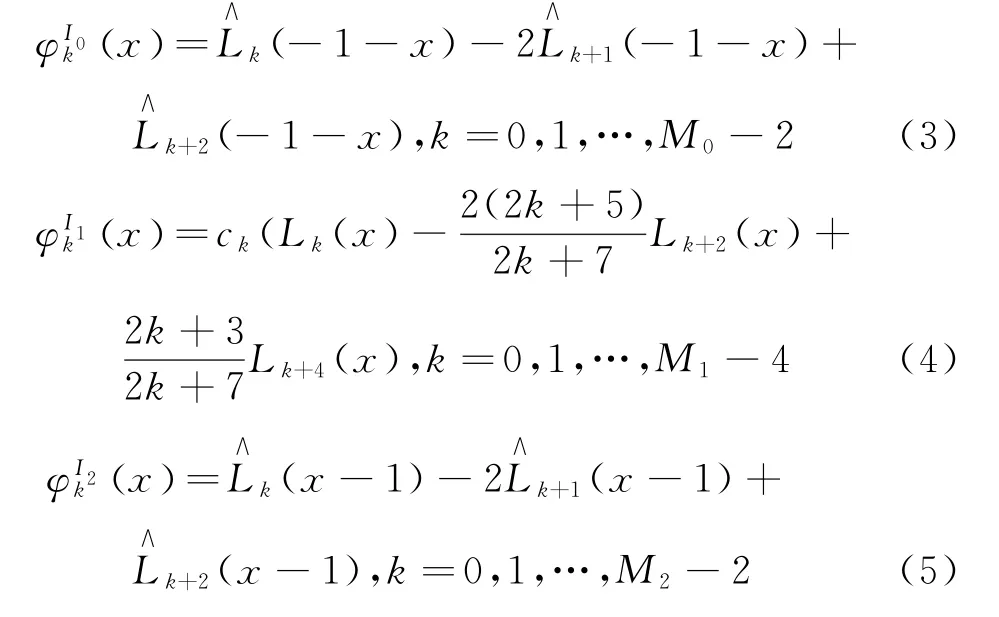
若记
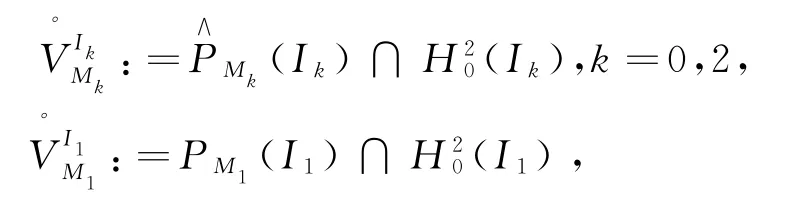
则由Laguerre函数以及Legendre多项式的正交性[2],容易验证

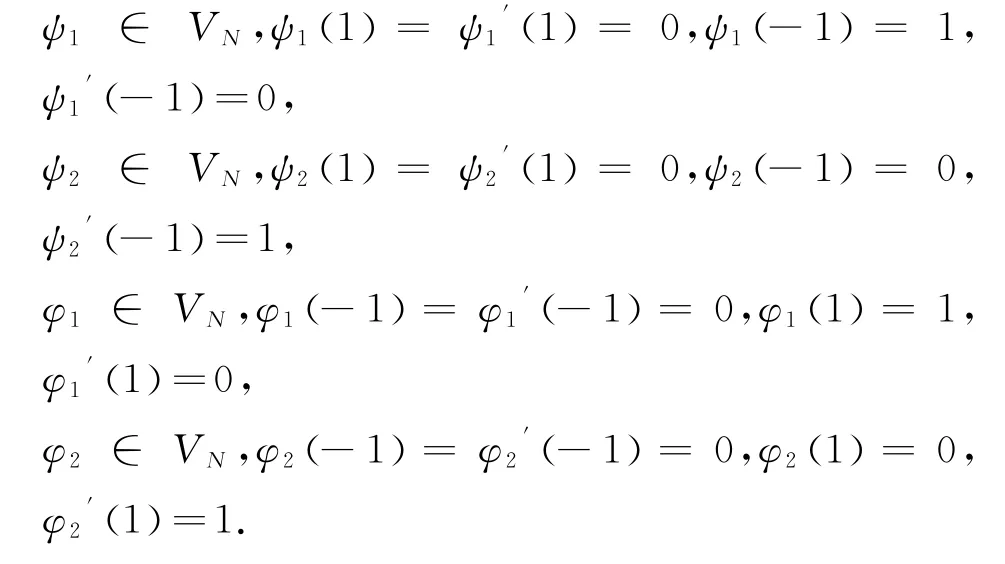
满足这些条件的一组函数可由如下形式给出
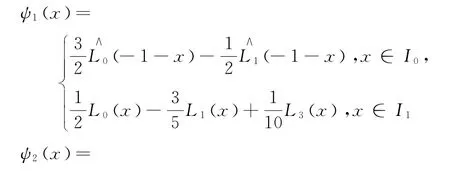
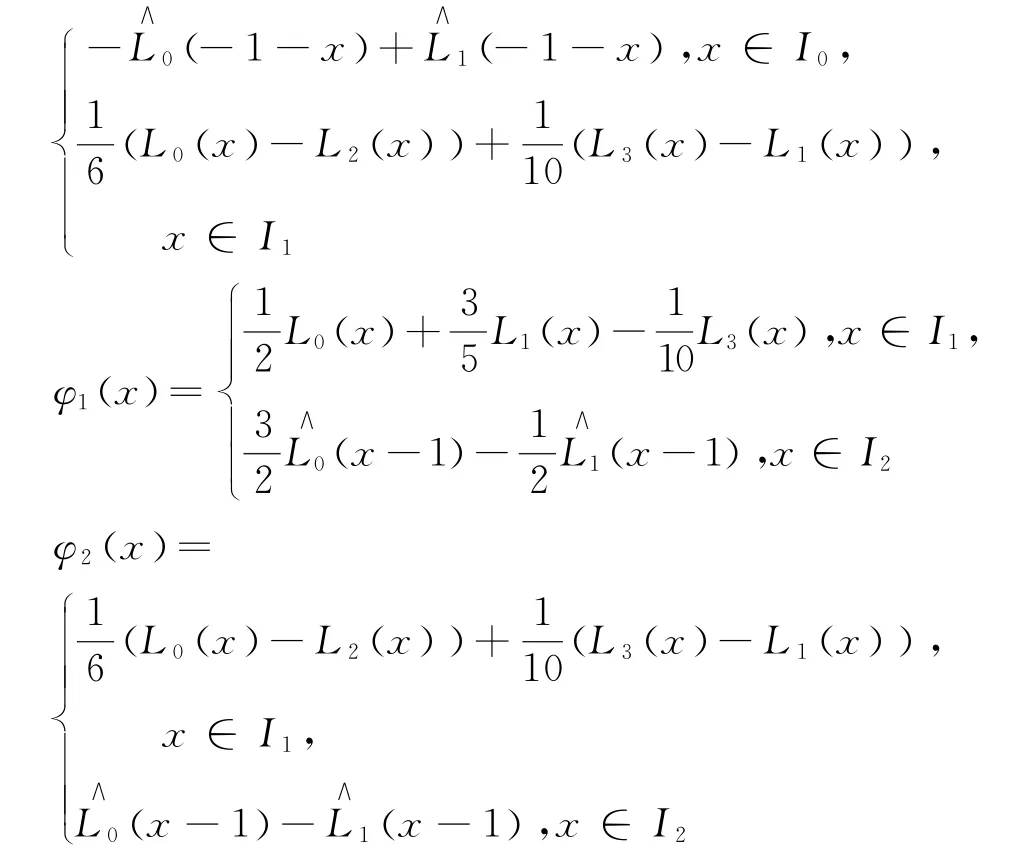
因此与问题(2)相关的线性系统的解可通过如下过程求得:
1) 构造关于双线性形式d(· ,·)的正交补.设是如下问题的解,如式(6):
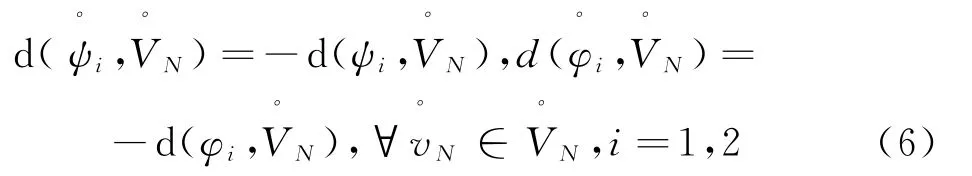
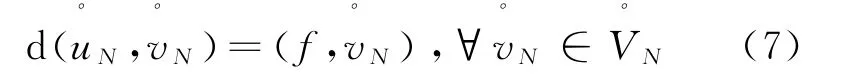
3)求解区域交面处的函数值及导数值u N(-1),u'N(-1),u N( 1),u'N( 1),如式(8):
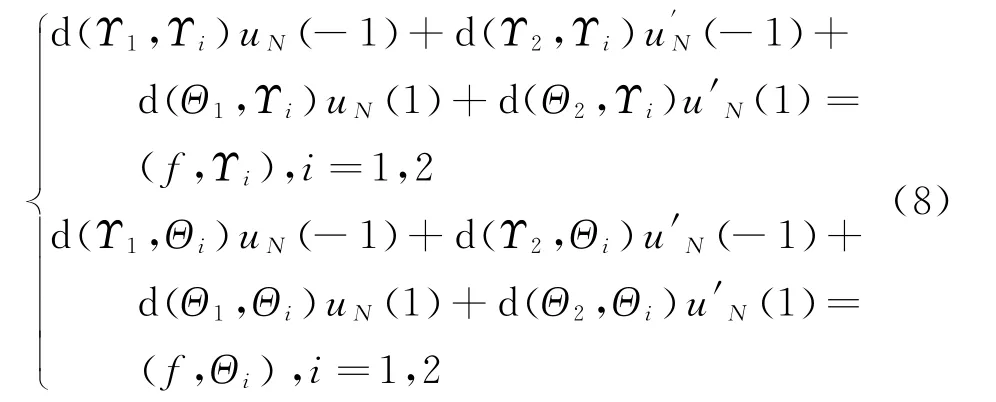
4) 确定问题(2)的解:由求(7)与(8)知,对任意的v N∈V N,
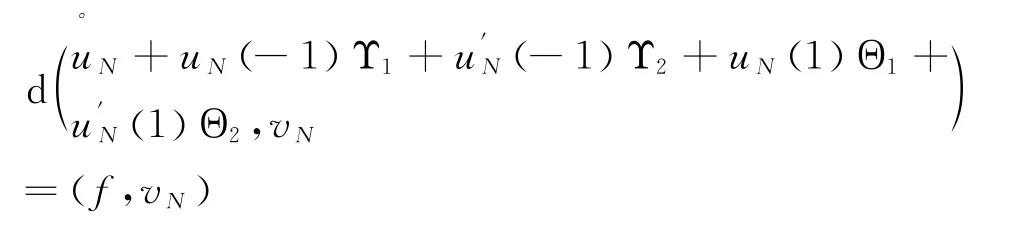
因此(2)的解为
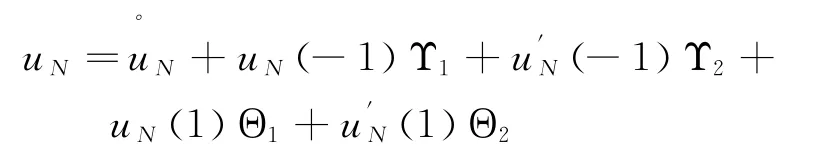
从以上的计算过程可知,把问题(2)的求解分解成一些相对独立的子问题的求解:单元内部子问题(6)和(7)以及单元交面信息子问题(8),因而更容易进行求解。
3 数值实验
算例1在问题(1)中固定λ1=λ2=1,并取其精确解为解析函数u(x)=1/(1+x2)h。
将 区 域 剖 分 为(-∞,-4],[-4,4],[4,∞)三部分,然后选取M0=M2=M=324,以使区间[-4,4]上的计算误差不受另两个区间计算误差的影响。图1给出的是半log尺度下,最大误差随M1的变化情况。由图可见,误差随M1呈指数e-c M1收敛。其次选取M1=128以使区间[-4,4]上的计算误差不影响另两个区间的计算误差。图2给出的是半log尺度下,最大误差随M的变化情况。由图可见,误差随M呈指数e-c M收敛。
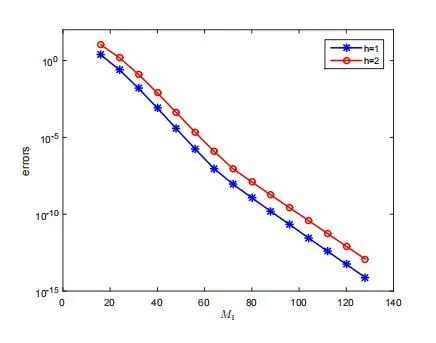
图1 误差随M 1的变化情况
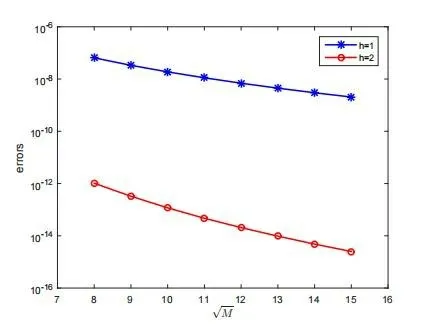
图2 误差随M的变化情况
下面对Lag-Leg-Lag复合方法和Laguerre函数法进行计算得到的误差进行比较。在复合方法中,取M0=M2=128,M1=128,在Laguerre函数法中,取M=512.图3给出的是h=1,2时两种方法计算得到的点点误差.。由图可见,复合方法用更少的点进行计算,还能得到比Laguerre函数法进行计算的效果更好,尤其是h=1时,复合谱方法在区间[-4,4]的逼近效果要比Hermite谱方法的逼近效果好得多。
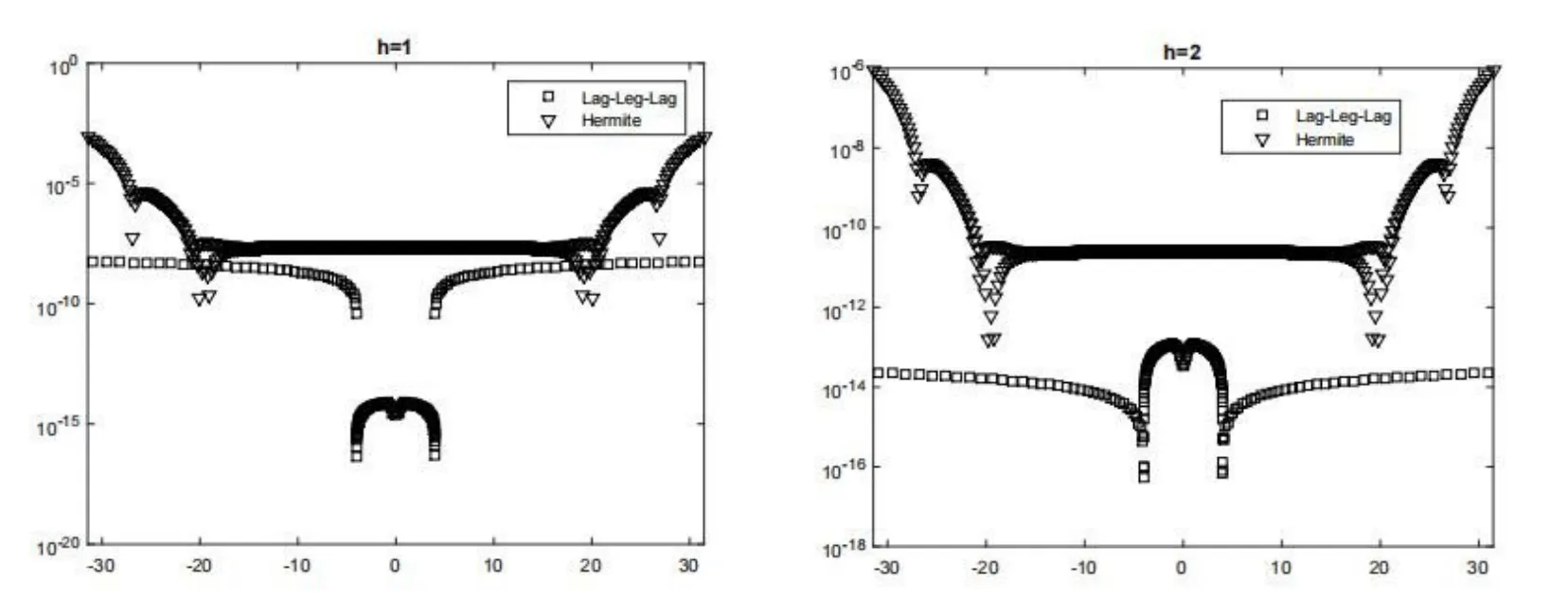
图3 两种方法计算得到的点点误差;左:h=1;右:h=2
4 结 语
提出了用Lag-Leg-Lag复合谱方法来处理全直线上的四阶方程,该方法结合了Legendre谱方法计算有界区域的高精度优点及Laguerre函数法解决无界区域的优点,避免人工边界的设置,并且可以灵活设置a1以及a2的值,是求解全直线上四阶方程数值解的一个选择。
