R(黎曼)积分的特征和意义分析①
2022-08-24高婷婷张明会
高婷婷, 张明会
(陇南师范高等专科学校初等教育学院,甘肃 成县 742500)
0 引 言
积分学是微积分的两大组成部分之一,《高等数学》中的积分包括不定积分和定积分(黎曼积分,简称R积分)两类积分,这是从两种不同的观点出发分别引进的积分,具体地说,不定积分是从逆运算的角度,把积分看作微分运算的逆运算;定积分则是从求极限的角度,把积分看作是一类特殊形式的和数的极限。建立积分概念的基本思想和步骤与微分概念的建立大体相同,但由于积分是一个反映“整体”的概念,而微分却是描述“局部”特性的概念,就导致了具体做法上的差异,具体地说,求函数y=f(x)在区间上的积分,一般分为如下四个步骤:第一步,“分割”,即从整体出发,将整体分割成许多局部(化整为零);第二步,“近似”,即在被分割的每一个局部范围内求出各个局部的近似值,用近似值代替真实值(以直代曲);第三步:“求和”,即用各个局部的近似值的和来求出整体的近似值(积零为整);第四步:“逼近”,即用取极限的形式求出整体的精确值。通过以上四个步骤不难发现:积分概念的建立和求积过程,也是采用了“化整为零”再到“积零为整”的迂回战术。通过这种迂回曲折的手段和途径,使得所求的整体,由未知转化为已知,实现了“直”与“曲”、“有限”与“无限”、“近似”与“精确”的矛盾转化,利用这种矛盾转化的规律性解决了用初等代数和几何方法无法解决的问题,创造了一个全新的数学方法,即定积分[1]。
1R(黎曼)积分的形成
定积分(黎曼积分)可以说是积分学(重积分、曲线积分、曲面积分以及其它积分)的基础,他是牛顿积分概念和柯西积分概念的基础上发展形成的。
(1)牛顿的积分概念
17世纪70年代,牛顿和莱布尼茨建立了他们的积分概念,同时他们也创立微积分学的理论基础——微积分基本定理,牛顿的积分概念是建立在函数的原函数存在的基础上的。
所谓f(x)在[a,b]上是牛顿可积的(简称N可积的),是指存在函数F(x),x∈[a,b],使其导函数F'(x)=f(x)在[a,b]上成立,这时称F(b)-F(a)为f(x)在[a,b]上的牛顿积分(N积分),记作,如式(1):
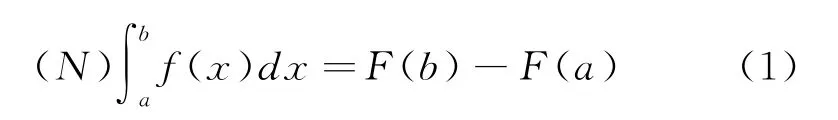
由于f(x)在[a,b]上N可积实质上与f(x)在[a,b]上存在原函数是等价的,因此,牛顿意义下的积分只能在有原函数的函数类上施行。所以,积分的实用性和广泛性受到很大限制,性质量好的函数,有些也是牛顿意义下不可积的。
(2)柯西的积分概念
在整个18世纪的漫长岁月里,由于欧拉和拉格朗日等人的大量工作,微积分在各个领域都取得了辉煌成就,尤其在力学领域更是重要,但微积分的奠基工作,直到19世纪,法国数学家柯西在1821-1823年间出版了他的《分析教程》和《无穷小计算讲义》(被认为是数学史上划时代的著作),才给出了分析学的一系列基本概念的精确定义,包括他的积分概念的独创性定义[2]。
设f(x)是[a,b]上的连续函数,记Δx=,作区间[a,b]的等距分划,如式(2):
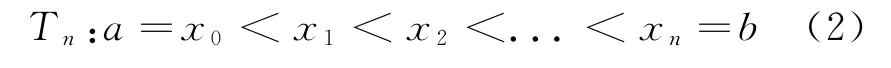
这里x j=a+jΔx(j=1,2,...,n),任取ξj∈(x j-1,x j)(j=1,2,...,n),作和如式(3):
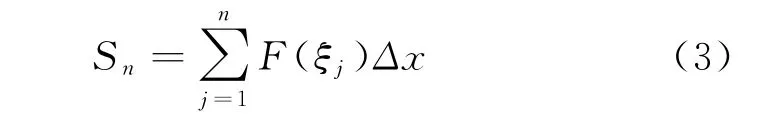
如果当n→∞时,极限=J存在,则称f(x)是[a,b]上是可积的(简称C可积),极限值J成为f(x)在[a,b]上的定积分,记作
柯西的积分定义已经是现在普遍使用的黎曼积分的雏形,整个积分过程经历了划分、求和、取极限的“三部曲”,定义建立在连续函数上,是构造性的,在定义的条件之下,可以证明积分和的极限必然存在,不需要再作可积函数类的讨论,但是,柯西意义下的积分,只能在连续函数上进行,人们自然会提出,除了连续函数外,什么样的函数还可以进行积分?这就首先必须对积分概念加以扩充,使积分概念与积分对象分离,然后在新的积分概念下去探求适合定义所要求的对象[3]。德国数学家黎曼最先研究了这一问题,提出了新的积分概念,即现在高等数学(数学分析)中通用的R(黎曼)积分。
(3)R(黎曼)积分的定义
先指出定义中涉及到的几个名词。
在区间[a,b]内任意插入n-1个分点,如式(4):
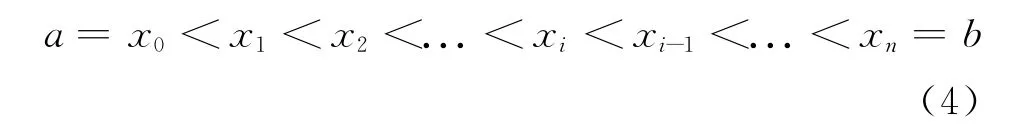
把[a,b]分成n个小区间这就说给定了[a,b]的一个分划T,记作:T={x0,x1,x2,...,x n}。
小区间Δi=[x i-1,x i]的长度记作Δi=x i-x i-1,称为分划T的模。
分划T的模刻画了分划T的细密程度,‖T‖越小,分划越细密,反之亦然,但是不同的分划却可以相同的模,同一个模可以对应无穷多个分划,也就是说模和分划不是一对一的[4]。
设函数f(x)定义于[a,b],对于分划T={x0,x1,x2,...,x n},任取ξi∈(x i-1,x i)(i=1,2,...,n),ξi称为介点,和式称为函数f(x)在区间[a,b]上关于分划T的一个积分和(黎曼和),由于ξi(i=1,2,...,n)可以在Δi上任意选取,对区间[a,b]上的一个确定的分划T,可以作出无穷多个积分和,f(x)在区间[a,b]上关于分划T的所有积分和的集合记作式(5):

定义:设函数f(x)是定义在[a,b]上的函数,J是常数,如果∀ε>0,∃δ>0,使对区间[a,b]上的任意一个分划T,只要‖T‖<δ,就有式(6):

则称f(x)在[a,b]上依黎曼意义可积分,简称R可积,称J为f(x)在[a,b]上的黎曼积分或者定积分,记作,或者记作J。如式(7):
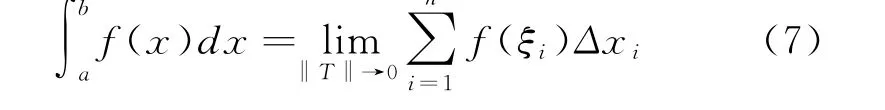
若‖T‖→0时,∑f(ξi)Δx i不趋于任何定值,就称f(x)在[a,b]上不可积,由于柯西积分和黎曼积分定义的结构形式雷同,但前者对被积分函数加了连续限制,对分划T加了等分限制,而后者却对被积分函数未加任何限制,所以R(黎曼)积分概念是柯西积分概念的直接推广,已知道存在一类有界不连续函数是黎曼可积的[5],另外,若f(x)在[a,b]上是N可积的,则f(x)必是R可积的,此时两种可积的意义是等价的,如式(8):

当然,一般情况下R积分和N积分并不相等。
在高等数学(数学分析)中,R积分被认为是够用的理想的积分概念,但是科学是不断发展的,由于实际的需要,R积分也显示出了它的一些弱点,例如R可积类的范围还不够广,因此又有一些新的积分概念出现,如勒贝格(Lebesgue)积分(常称为L积分)就是其一,它较R积分更为一般,不过,R积分更加自然和易解易懂,因此现代对于广义黎曼积分的研究也受到了人们的重视[6]。
2 不定积分与R(黎曼)积分的关系
函数f(x)在区间I上的全体原函数构成的集合,称为f(x)在区间I上的不定积分,记作式
(9):
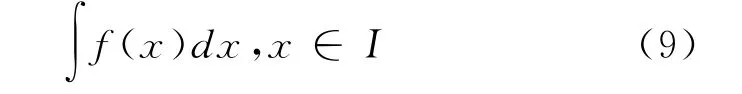
这里有两个问题,一是存在性,即哪些函数存在原函数;二是求法,即如果原函数存在,如何找出其原函数,要从根本上解决这两个问题,最终都要借助于“定积分”这个工具[7]。
关于存在性的讨论,一条途径是从微分介值定理得出的,即“有第一类间断点的函数不存在原函数”;另外,是利用活动上限的定积分所定义的函数,只要f(x)连续,则f(x)的原函数一定存在,而且F(x)就是其中之一。
关于求法问题,一是从不定积分的定义出发,如式(10):
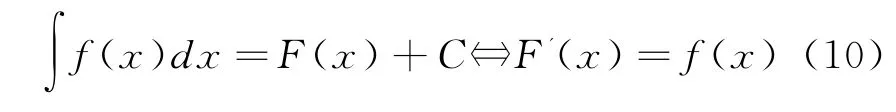
所以,从每一个求导公式就可以“翻译”一个相应的求不定积分的公式,但是,这样的倒推法还不能解决全部的求和问题,这一点与微分法不同[8],例如,根据导数的定义及微分法则可以求出全部初等函数的导数,然而根据不定积分定义和积分法则,即使对某些简单的初等函数的不定积分也无能为力,问题在于导数定义本身给出了求导数的一个构造性算法,而不定积分的定义却没有这个特点,同时更重要的是所有的初等函数的导数仍是初等函数,但不少初等函数的不定积分却不是初等函数,因此,还需要另找办法去解决。
设函数f(x)在I上不定积分存在,原函数为F(x),已知在某点x=a的值为F(a),如微分中值公式(11):
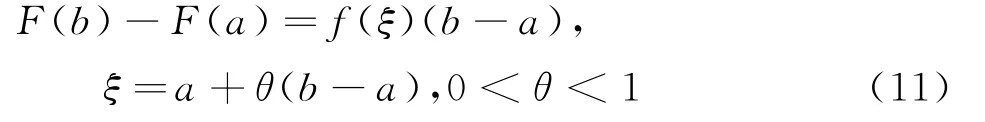
其中b∈I,因为当b-a较大时,ξ的位置难作准确定位,从而F(b)的值就更难准确估计,将[a,b]等分为n个小区间,Δi=[x i,x i+1](i=0,1,2,...,n-1),x0=a,x n=b,则式(12):
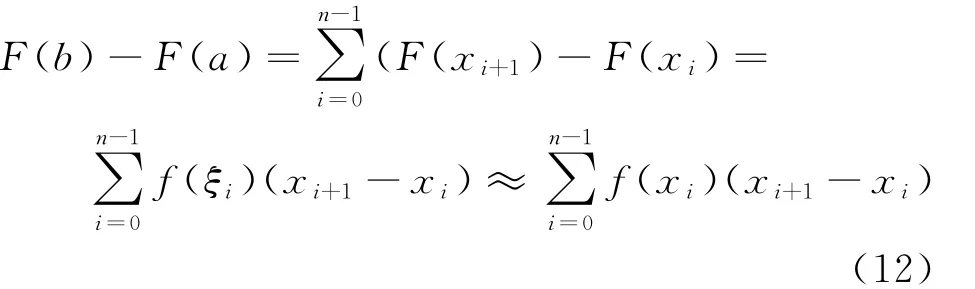
其误差为式(13):
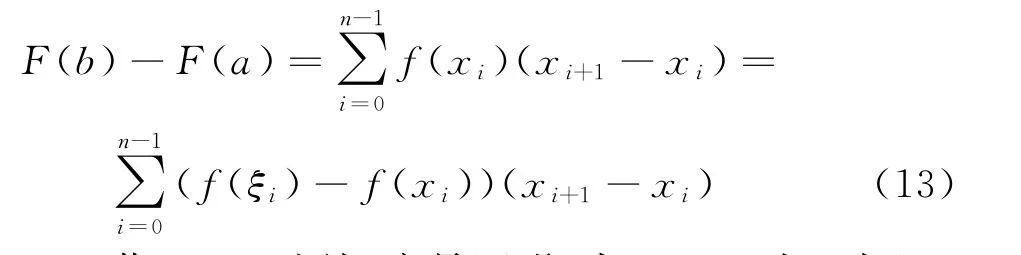
若f(x)连续,容易证明,当n→∞时上式以0为极限,如式(14):

这就将求原函数两点差值的问题转化为求和数的极限,即定积分的问题了,改b为x则有式(15):
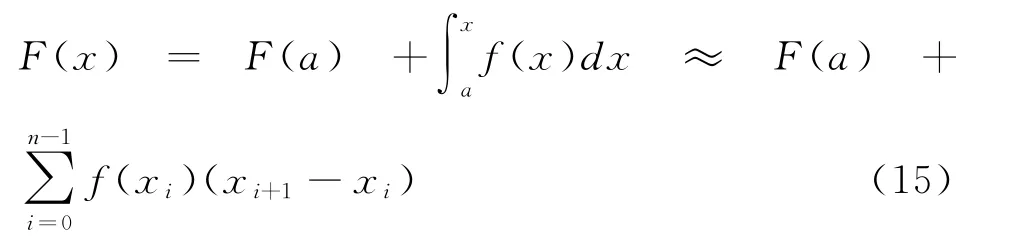
这从原则上给连续函数的原函数给出了一条构造性的定义和算法,基本上解决了连续函数的不定积分的求法问题。
3 结 语
在上述分析的基础之上,从更深层次即哲学的角度看出数学分析的基本方法---极限方法。这些对立统一规律、整体与局部规律、量变与质变矛盾变化规律等基本哲学思想在数学分析中的具体体现和运用,为进一步研究利用数学建模思想对陇南电商助力乡村振兴战略的分析与模式研究提供了新的思路和方法。
