基于贝叶斯优化与改进LeNet-5的滚动轴承故障诊断

汤 亮， 凡焱峰， 徐适斐， 蔡凯翼

(1.湖北工业大学 机械工程学院，湖北 武汉 430068; 2.湖北省制造业创新方法与应用工程技术研究中心，湖北 武汉 430068)

1 引 言

滚动轴承是机械传动装置的重要零件，其故障诊断是机械传动装置能稳定运行的重要保证，因此准确判断轴承故障对机械传动装置的正常工作意义重大。但机械传动装置结构复杂，滚动轴承的振动信号具有非线性、非平稳性的特点，所以传统的故障诊断方法难以精确判断滚动轴承的故障类型[1]。

采用机器学习如人工神经网络、支持向量机和随机森林等实现滚动轴承故障识别，这些故障诊断运用小波变换、傅里叶变换等时频变换提取滚动轴承的原始振动信号的故障特征，通过分类器中实现滚动轴承的故障诊断。郑新等使用经验模态分解和主成分分析实现了轴承故障诊断模型的构建[2]；通过对变分模态分解改进，孟宗设计了高精度的故障诊断模型[3]；利用局部均值分解与随机森林，周海军设计了样本熵与随机森林分类的滚动轴承故障诊断[4]。但这些方法存在操作过程复杂、忽略特征提取和分类联系的问题，这导致传统故障诊断无法保持较高的精度。

深度学习可以提取原始样本中的特征信息，具有良好的非线性拟合能力，卷积神经网络(convolutional neural network, CNN)的权值共享结构降低数据重建的复杂性，在处理原始样本具有先天性的优势，在语音识别[5]、图片分类[6]等领域具有广泛应用。

CNN在滚动轴承故障诊断中应用广泛。对滚动轴承振动信号完成傅里叶变换，熊剑等把频谱样本划分后，构建高精度滚动轴承故障诊断模型[7]；Lu等将一维信号转换成二维数据作为CNN的原始输入构建故障诊断模型[8]；将滚动轴承振动信号转换成二维信号后，Wen等提出具有高鲁棒性的LeNet-5的轴承故障诊断模型[9]；刘星辰等以滚动轴承振动信号作为输入，提出高精度的一维CNN故障诊断模型[10]；Zhang等考虑了滚动轴承的实际工作环境中存在大量噪音后，设计高鲁棒性的故障诊断模型[11]，该模型在多工况下保持较高精度；利用随机对角线优化CNN的结构，Viet提出多工况下高精度的滚动故障诊断模型[12]。然而，上述CNN对轴承故障诊断的研究，都采用人为提取的特征作为CNN的输入，导致故障识别率无法提升，且特征提取的过程依赖人工经验。

本文设计了采用贝叶斯优化的改进LeNet-5网络算法以及基于该算法构建的轴承故障诊断模型，利用该轴承故障诊断模型实现轴承故障识别。使用该网络模型对滚动轴承实现故障诊断中，旨在为轴承故障诊断提供理论和技术支持。

2 LeNet-5网络

LeNet-5作为典型的CNN，利用局域感受野，权值共享和池化特性实现输入的特征提取。LeNet-5网络实现分类的过程分为特征提取和分类2部分：通过卷积和池化操作实现振动信号的特征提取；通过全连接层和径向基(radial basis function, RBF)实现分类。LeNet-5网络结构如图1所示。

图1 LeNet-5卷积神经网络结构

卷积层利用卷积运算实现原始输入的特征提取[13]。卷积运算过程如式(1)所示:

(1)

池化层采用降采样技术实现输入信号特征的降低，避免过拟合现象[14]，提高容错性。池化层的计算过程可由式(2)表示：

(2)

全连接层与最后的池化层采用全连接的方式[15]，全连接层计算工程由式(3)表示：

(3)

LeNet-5网络有7个网络层：原始输入为32×32；C1层,6个大小为5×5的卷积核，卷积结果由6个28×28的二维信号组成；S2层，以2×2的邻域作为池化区生成6个14×14的二维信号，激活函数为Sigmoid函数；C3层，具有16个5×5的卷积核，其输出由16个为10×10的二维信号组成；S4层，以 2×2的邻域为池化区生成16个5×5的二维信号，激活函数为Sigmoid函数；C5层,输入与其卷积核相等，卷积后输出为1×1；全连接层F6,包含84个神经元，激活函数为Tanh函数；RBF组成LeNet-5网络的输出层。

3 贝叶斯优化

贝叶斯优化是利用贝叶斯搜寻目标函数最优值的算法[16]。概率代理模型和采集函数是贝叶斯优化算法的核心部分，常见的概率代理模型有高斯过程；采集函数由目标函数的后验概率组成，为了使总损失r为最小，贝叶斯优化算法利用采集函数选择评估点xt，该过程由式(4)和式(5)表示。

(4)

ri=|y*-yi|

(5)

式中：X为决策空间；λ(x,D1:i)为采集函数；y*为最优解。

贝叶斯优化算法由以下步骤实现：

(1) 确定最大迭代次数N；

(2) 利用采集函数获得评估点xi；

(3) 利用评估点xi评估目标函数值yi；

(4) 整合数据Dt后更新概率代理模型；

(5) 若当前迭代次数n最大迭代次数N，则返回步骤(2)继续迭代，否则输出xi。

4 贝叶斯优化与改进LeNet-5的故障诊断模型设计

与经典LeNet-5网络对比，本文的LeNet-5网络主要有以下改进：

(1) 批归一化可以避免网络的梯度弥散，同时增加神经网络的泛化能力[17]，采用批归一化操作对S1，S2池化层输出特征进行归一化处理，降低输出特征的差异性；

(2) Relu激活函数避免了Sigmoid函数的梯度消失现象[18]，有易优化、增加网络稀疏性的优点，将LeNet-5网络中池化层S2和S4的激活函数由Sigmoid函数改为Relu函数；

(3) 全局平均池化与全连接层相比，降低了LeNet-5网络的参数量，整合了全局空间信息，使网络鲁棒性更高[19]，将LeNet-5网络全连接层F1替换成为全局平均池化层；

(4) Softmax函数分类效果更好，Softmax函数代替LeNet-5网络中的RBF实现特征。

随机选择的学习率，训练批次和优化器可能导致改进LeNet-5网络在滚动轴承故障诊断能力不足，因此以训练一定次数后准确率为目标函数，以一定范围内的学习率，训练批次和不同优化器为决策空间，利用贝叶斯优化算法对这些超参数进行优化。

5 实验分析

5.1 CRWU轴承数据集

本文用美国凯斯西储大学滚动轴承数据集[20]对贝叶斯优化后的改进LeNet-5网络开展实验验证，试验台装置包括电动机、扭矩传感器、功率测试计。SKF6205滚动轴承安装在电动机驱动端，加速度计传感器的采样频率设为12 kHz，在多种转速下(1 797，1 772，1 491，1 750 r/min)采集滚动轴承原始振动信号，滚动轴承故障类别共3种：外圈故障，内圈故障和滚动体故障，每种类型的损伤尺寸都有3种：0.07，0.14，0.21 inch(1 inch=2.54 cm)。0.21 inch又分为中心方向、正交方向、相对方向3种故障损伤类型，本文同时考虑中心方向、正交方向和相对方向的外圈故障损伤类型。

LeNet-5网络输入为32×32的二维数据，同时也为了提高卷积层的计算速度，将1 024个采样点作为一个采样周期，采用形变操作将1 024×1的一维数据转化为32×32的二维数据。在内圈故障，外圈故障和滚动体故障约有487 093/1 024≈480个样本；1 797 r/min转速下，正常(作为一种特殊的故障)状态约243 938/1 024≈238个样本，而其余转速下正常状态约485 643/1 024≈475个样本。为了保证各类故障样本数相同，在这些正常样本中随机选择480个样本作为训练时的数据集。本文共考虑12种故障类别，滚动轴承故障，故障类别，损伤直径以及样本数如表1所示。

表1 驱动端轴承故障数据

5.2 数据集预处理

为了保持原始振动信号相对不变，提高故障分类的准确性，运用Z-score标准化对样本中原始振动信号进行处理，如式(6)所示:

(6)

为了确保网络模型具有较强的泛化能力，将归一化处理后的数据集D依照7:2:1的比例，被分为训练集S，验证集V和测试集T。

5.3 对比方法说明

本文所有实验都基于深度学习框架Tensor Flow2.0实现，计算机配置为i5-7500CPU，主频为3.4 GHz。实验中，训练过程中导入时间监控机制来记录3种网络训练的时长。

5.3.1 一维CNN(1D-CNN)

1D-CNN采用的是曲建山等提出的基于一维卷积神经网络的滚动轴承故障诊断模型[21]，该网络模型输入为1 024×1的一维数据，其部分网络结构参数如表2所示。

表2 1D-CNN网络结构参数

1D-CNN的准确率随迭代次数变化曲线如图2所示。

图2 1D-CNN准确率变化曲线

5.3.2 二维CNN(2D-CNN)

2D-CNN利用李益兵等提出的混合蛙跳算法优化的CNN的滚动轴承故障诊断模型[22]。该模型仅采用了1 797 r/min转速下的轴承10种不同故障的数据。其部分网络结构参数如表3所示。

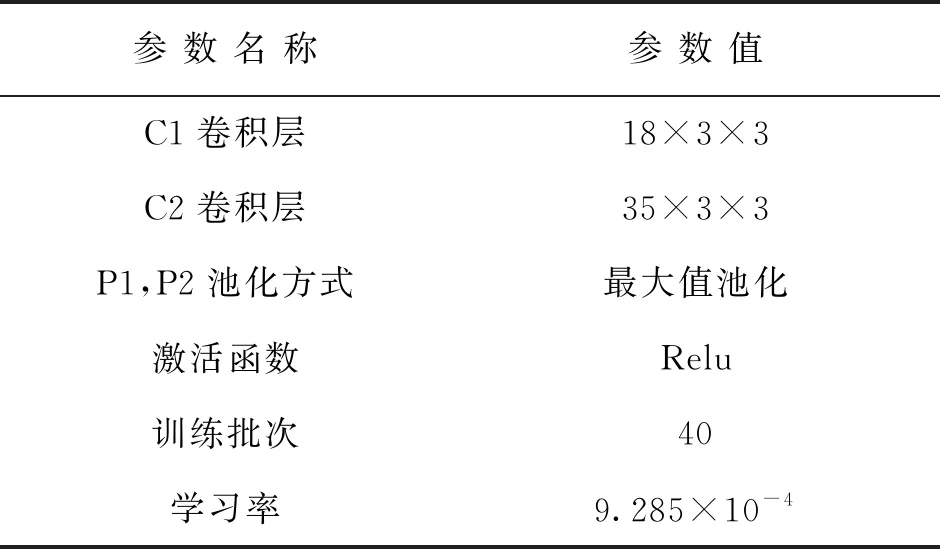
表3 2D-CNN网络结构参数

2D-CNN的准确率随迭代次数变化曲线如图3所示。

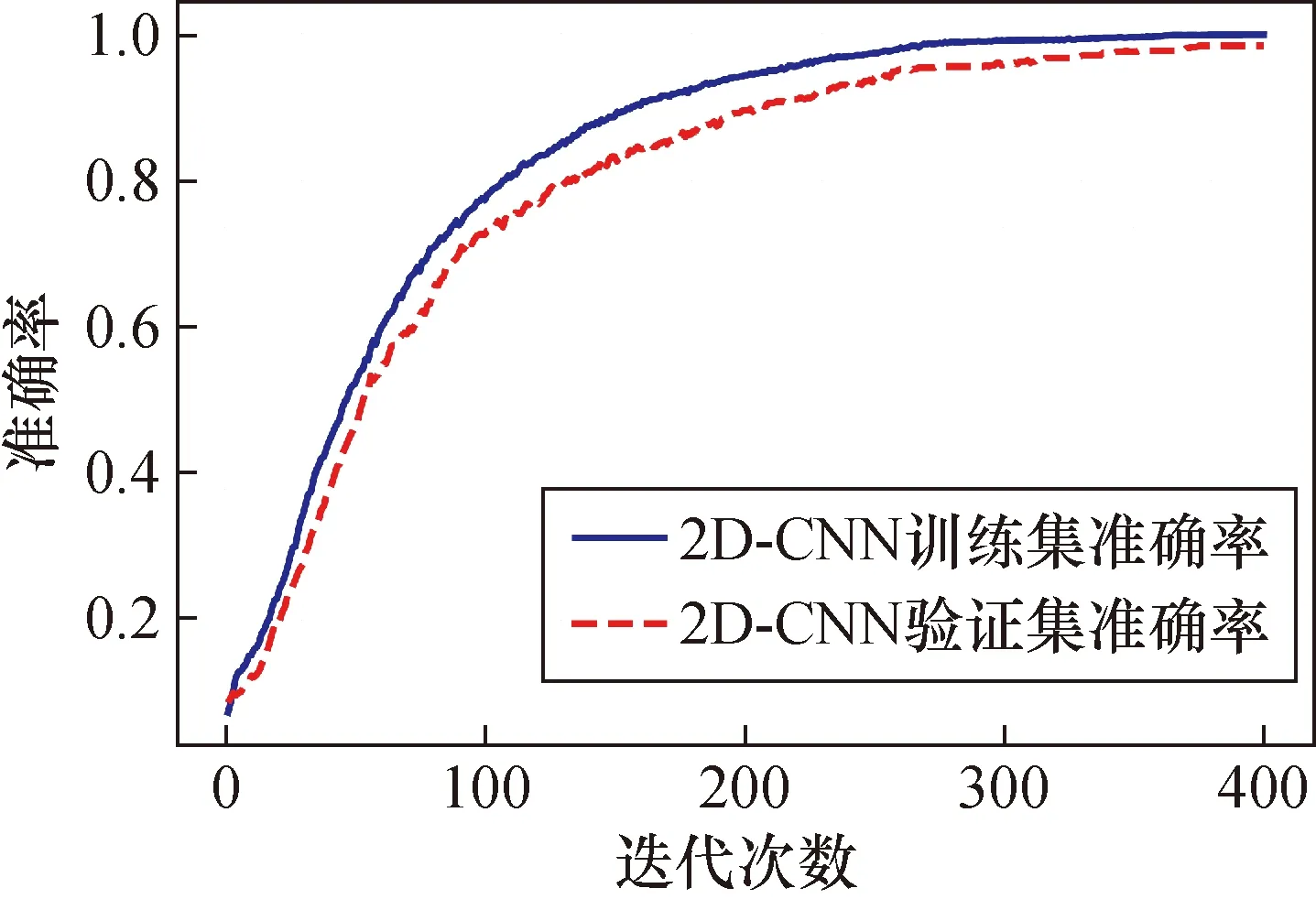
图3 2D-CNN准确率变化曲线

5.3.3 改进LeNet-5网络

利用贝叶斯优化对学习率等超参数进行优化，最大迭代次数设为40，采集函数为期望提升，决策空间如表4所示。

表4 改进LeNet-5网络的超参数及其范围

经过贝叶斯对超参数优化后可得：训练批次为32，优化器采用RMSprop，学习率为1.724×10-3。优化后的改进LeNet-5网络(BO-ILeNet-5)部分结构参数如表5所示。

表5 改进LeNet-5网络结构参数

利用BO-ILeNet-5网络开展实验验证，准确率变化曲线如图4所示。

图4 BO-ILeNet-5准确率变化曲线

5.4 对比与分析

经实验分析，BO-ILeNet-5网络模型与1D-CNN 和2D-CNN对比结果如表6所示。

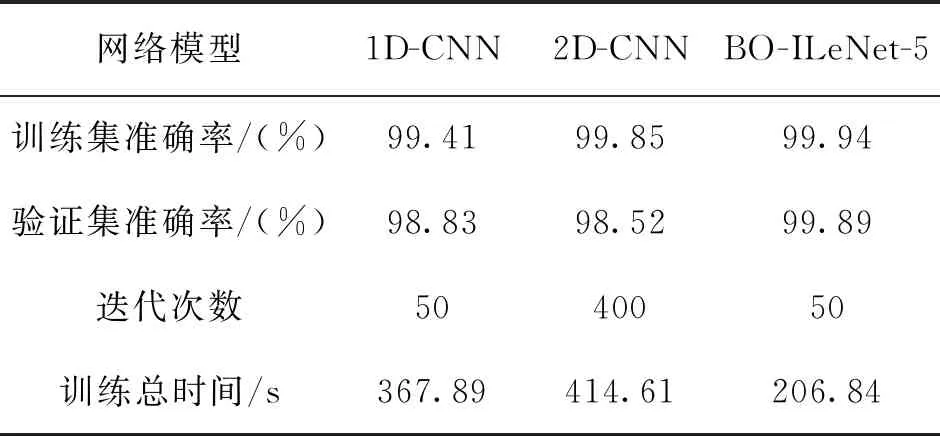
表6 故障识别模型对比

BO-ILeNet-5网络具有较高的精度，无论在训练集还是在验证集上，BO-ILeNet-5网络对滚动轴承的故障诊断比1D-CNN 和2D-CNN更好，且训练效率更高。

为了验证BO-ILeNet-5网络的泛化能力，利用测试集T进行验证，测试集中每类故障均有48个样本，并绘制故障分类混淆矩阵如图5所示。混淆矩阵的横轴表示故障诊断模型对样本进行预测的故障类别，纵轴表示样本真实的故障类别，对角线表示正确识别的原始样本数，非对角线表示识别错误的样本数，由图可知：仅在0.21 inch的滚动体故障和外圈故障中心方向各存在1个样本在预测中出现错误。结果表明，BO-ILeNet-5网络对滚动轴承故障有较好的分类效果。

图5 BO-ILeNet-5故障混淆矩阵

为验证BO-ILeNet-5网络的鲁棒性，在测试样本中加入不同程度的高斯白噪声，测试不同信噪比(signal noise ratio，SNR)下的识别准确率，结果如表7所示。

由表7可知，BO-ILeNet-5网络在低噪声下故障识别准确率更高。

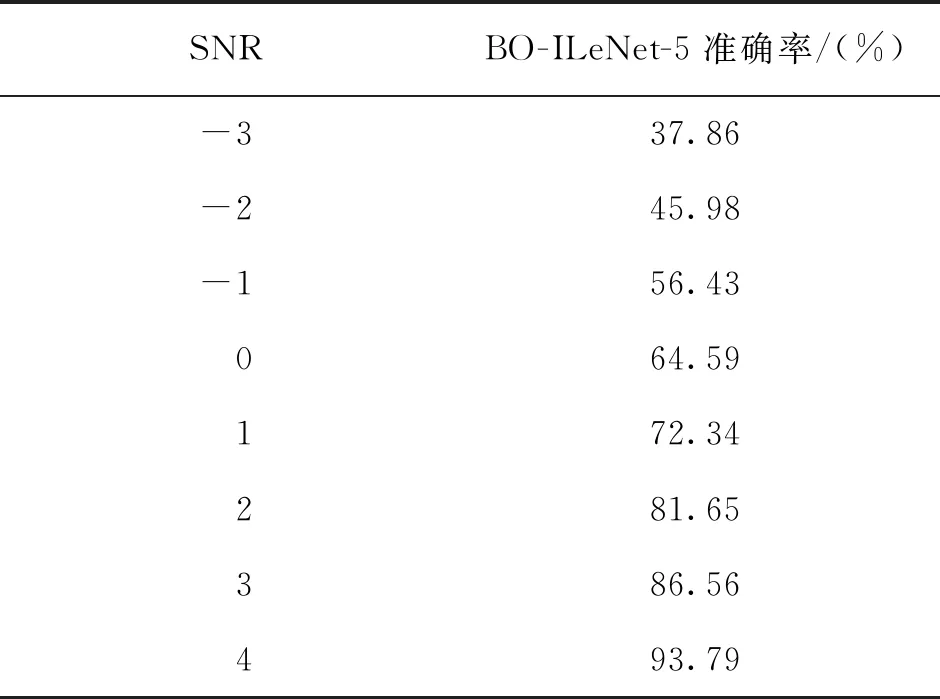
表7 BO-ILeNet-5不同噪声环境下准确率

6 结 论

传统的CNN应用在轴承故障诊断上存在效率低、精度差的问题。本文首先改进LeNet-5网络中网络层的激活函数，引入批归一化操作，全局平均池化避免网络模型出现过拟合，并用贝叶斯优化改进LeNet-5网络的超参数，最后采用该算法构建的轴承故障诊断模型，经过对比实验分析，获得以下结论：

(1) 基于贝叶斯优化超参数后的改进LeNet-5网络的滚动轴承故障诊断模型不需要手动提取轴承原始振动信号的特征，降低了对人工经验和专家知识的依赖。

(2) 基于贝叶斯优化超参数后的改进LeNet-5网络滚动轴承故障诊断模型具有较好泛化性能和较高的故障识别率，且网络模型训练时间较短。

在进一步的研究中，应该采用自测的滚动轴承的多种故障信号来对该轴承故障诊断模型进行工程实践研究，以提高网络模型的实际应用价值。