分布式光伏系统无功控制策略研究

沈晓倩，李鹏涛，宋丹

（国网宁夏电力有限公司石嘴山供电公司，宁夏 石嘴山 753000）

0 引言

随着化石能源的逐步枯竭，以及全球气候变化问题日益严峻，尽可能高效地利用可再生能源日益受到各国政府的广泛关注，大规模可再生能源发电并网已经成为新型电力系统不可抵挡的发展趋势[1]。由于分布式光伏发电系统被直接并入配电网，因此具备配置灵活、就地消纳、投资和损耗较小等特性，具有突出的经济效益和社会效益。然而光伏发电并网会对低压配电网产生诸多弊端：因典型居民负荷的高峰时段与光伏发电出力较大的时段经常不能匹配，所以造成低压配电网白天容易面临过电压风险，而夜间容易面临欠电压风险，同时还会造成网络损耗的增加[2]。并且，由于光伏发电具有波动性和间歇性的特点，会对配电用户的用电质量产生影响，因此，亟需研究分布式光伏并网系统无功控制方法，提高光伏并网发电系统的供电质量。文献[3]基于电压-有功功率的下垂系数，选择节点的有功切除量，避免并网点电压发生越限。文献[4]通过削减分布式光伏系统有功功率，同时借助逆变器剩余无功功率容量，对节点越限电压进行治理。文献[5]提出削减直流侧有功出力控制并网点电压不发生越线，然而这种控制方法却以降低经济效益为代价满足电压控制。

针对上述情况，基于德国电气工程师协会提出的4种分布式光伏并网无功控制策略，通过对分布式光伏系统无功功率和功率因数的控制，实现对配网点电压的控制。通过研究4种控制策略，对其进行仿真分析，从仿真结果可知，控制方案实现了对电压越限的控制。

1 光伏逆变器无功输出模型

1.1 分布式光伏并网电压特性

分布式光伏系统为光伏阵列PV产生的电压输送给由最大功率控制MPPT(maximum power point tracking)电路控制的DC/DC直流斩波电路，升压后输送给由控制器控制的DC/AC逆变电路，逆变后的三相交流电压并入电网，构成整个光伏发电并网系统。图1为分布式光伏并网系统线路简化模型。

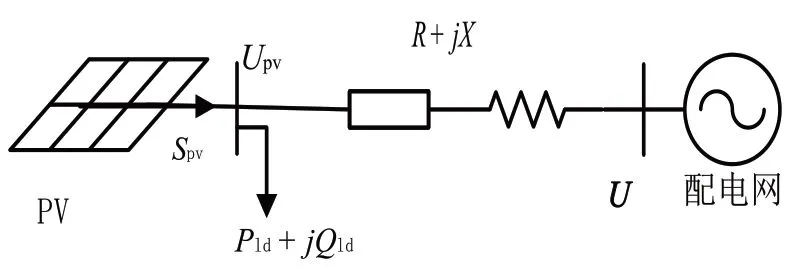
图1 分布式光伏并网系统线路简化模型

根据基尔霍夫定律可得出逆变器和电网的变量关系，进而分析并网逆变器的无功输出。设电网电压U为参考向量，通过计算可得：

式中：PPV、QPV—光伏系统发出的有功和无功功率；

Pld—本地的有功负荷；

Qld—本地的无功负荷；

UPV—并网点电压；

R、X—线路阻抗。

由于UPV的虚部分量远小于实部分量，为简化计算，可将其虚部略去，故式（1）可化简为

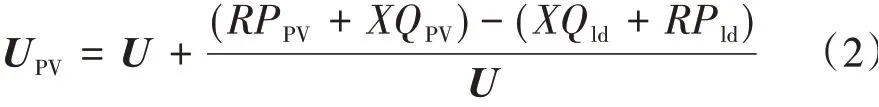
系统本地负荷一般多为感性负荷，所以Pld和Qld均大于零。

1)当光伏系统没有接入配电网时，其输出有功功率PPV和无功功率QPV均为0，将其分别带入式（3）可以得到：

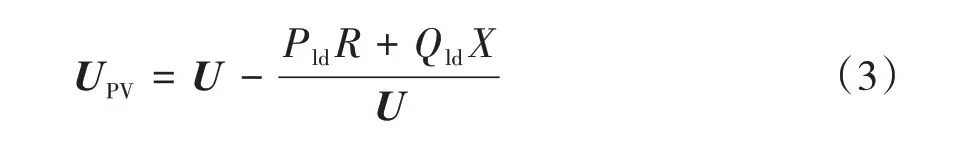
由式（3）可知，此时并网点电压UPV不会超过系统电压U，即不发生电压越限问题。

2)当光伏系统接入配电网，并在功率因数cosφ=1模式下运行时，光伏系统的有功输出PPV最大，无功输出QPV为0，将其带入式（4）可以得到：

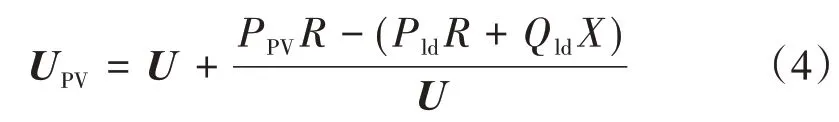
当(PPV-Pld)R-QldX≤0，此时并网点电压UPV不会超过系统电压U，即不发生电压越限；当系统的有功输出PPV增大，使(PPV-Pld)RQldX＞0，此时并网点电压会反超系统电压U，如果并网点电压越限不及时采取措施，将造成用电设备严重损坏。

综上所述：影响并网点电压UPV的因素主要包括有功出力PPV、无功出力QPV、本地负载Pld以及线路电阻R和线路电抗X。本地负荷Pld由用户决定，具有不可控性；R和X与光伏发电系统并网的位置相关，一般为固定值；光伏的有功出力PPV和无功出力QPV可以进行调节，具有可控性，实现对并网点的电压控制。

1.2 光伏逆变器无功输出约束

分布式光伏系统逆变器的无功输出容量有限，无功功率受逆变器容量及并网点电压的约束[6]。逆变器向配电网输出的有功功率P和无功功率Q为

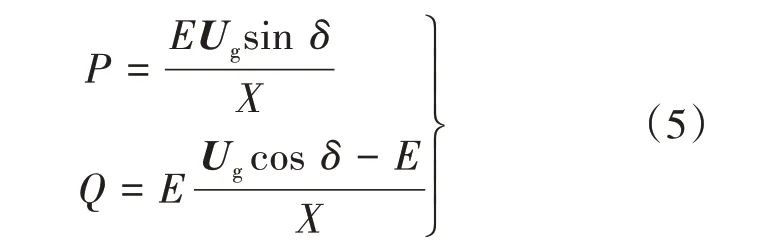
式中：Ug—逆变器输出相电压；

E—电网相电压；

δ—Ug和E的夹角。

将式（5）处理可得：

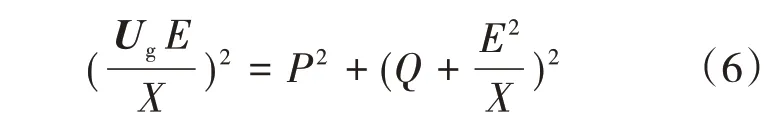
将式（6）整理可得无功Q的约束条件1：

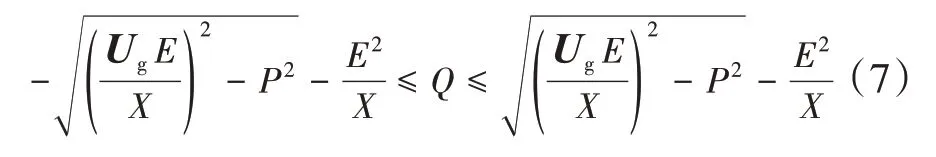
根据功率平衡关系S2=P2+Q2整理可得无功Q的约束条件2：

根据式（7）和式（8）的两个约束条件可知：无功功率与有功功率、视在功率、逆变器输出电压、电网相电压、线路电阻及线路电抗有关。

2 无功功率控制策略

2.1 恒无功功率控制

恒定的无功功率值根据外界环境及系统负荷设定。根据其负荷曲线和出力曲线设定无功参考值，以保证功率因数的合理性及并网点电压不越限[7]。当光伏有功出力和线路负荷出力已知，可根据并网点电压求出光伏系统发出的无功功率：

据此可得光伏逆变器发出的无功功率QPV范围。

2.2 恒功率因数控制

恒功率因数cosφ控制策略下并网的无功功率与有功功率比值为一个恒值C。

恒功率因数cosφ控制下，当光伏逆变器的有功出力PPV很小，即PPV＜Pld时，线路电压会随着馈线潮流的方向下降，虽然并网点电压并未越限，但为维持功率因数cosφ不变，无法避免会发出一定的无功功率[8]。

2.3 基于光伏有功出力控制

基于光伏有功出力的无功功率控制，即cosφ(P)控制，其功率因数cosφ值基于光伏有功出力改变，cosφ(P)控制特性曲线用一阶函数可表示为

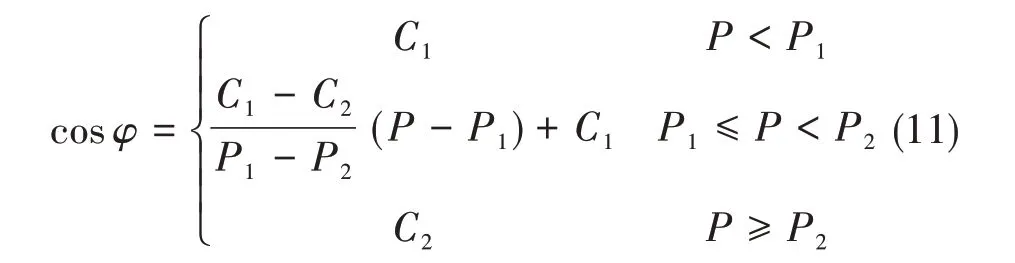
当有功出力低于额定值Pm一半时，系统仍以cosφ=1并网，即P1=Pm/2，C1=1；当有功出力达到额定值时，最小功率因数设置为cosφ=0.9，即P2=Pm，C2=0.9[9]。

2.4 基于并网点电压控制

分布式电源接入配电网后，由于光伏系统发电的不确定性，不仅会引起并网点电压升高，产生电压越限，还会使整个系统的潮流方向变为双向流动，网络的电压分布的规律性被打破。传统的基于本地测量信息以实现电压控制的设备已不再适用。当有功出力小于额定容量时，若电压越限，可以通过无功调节参与电网电压控制。为了使电网电压仍能保持在安全范围内，提出基于并网点电压幅值的无功控制策略[10]。

基于采集并网点电压U，确立无功参考值,Q(U)控制策略特性的表达式为

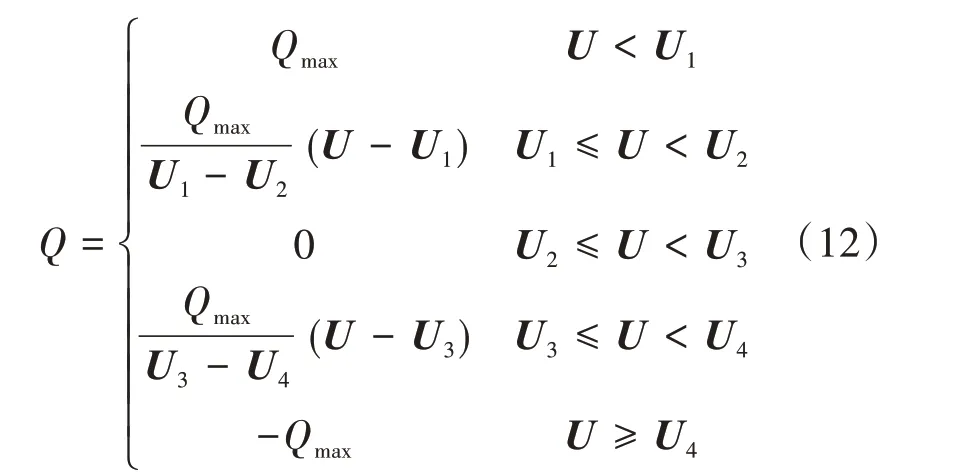
U1、U2、U3、U4表示的电压值分别为0.95、0.98、1.02、1.05p.u.；Qmax为光伏系统无功输出最大值[11]。

3 仿真分析

分布式光伏系统的出力因受外部环境的影响，从而影响并网点电压，通过仿真考虑外部环境急剧变化时无功控制策略对并网点电压的控制效果。由于分布式光伏系统出力主要受光照强度和温度影响，设置场景一和场景二，当外部环境由场景一在2.5 s内变换到场景二，分析4种控制下的并网点电压UPV、功率因数cosφ、逆变器输出的无功功率Q变化状况，场景状况如表1所示。

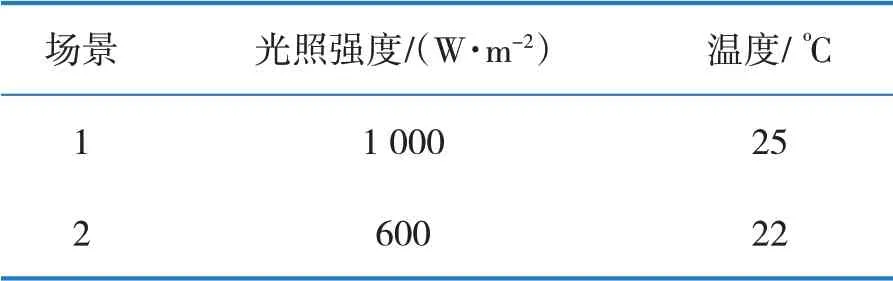
表1 不同场景下光伏系统外部状况

并网点电压会在场景变化过程中电压下降，当外部环境波动较小时电压会恢复至设定值，其中，基于并网点电压控制，并网点电压在场景变化过程中电压下降达15.6 V，并且电压低于设定电压5 V左右，较其他控制方法对并网点电压控制效果较差，并网点电压波形如图2所示。

图2 不同控制下的并网点电压

场景变化造成功率因数会发生骤降，在0.1 s左右会有一定的回弹进而趋于稳定；外部因素趋于稳定时，功率因数也会上升恢复场景变化前功率因数水平。恒无功功率控制在场景变化过程中功率因数变化剧烈，差值达0.64，不满足功率因数要求，场景变化下功率因数曲线如图3所示。

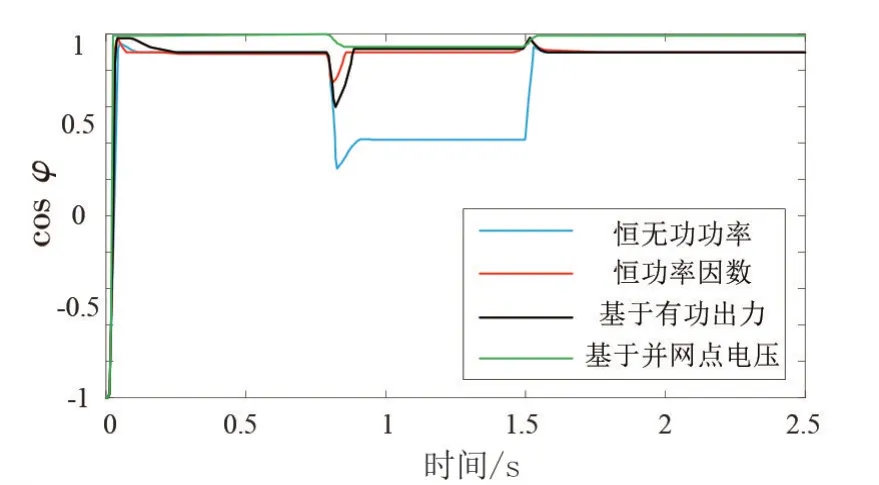
图3 同控制下的功率因数

无功功率在场景变化下，恒无功功率控制保持恒定无功输出，基于并网点电压控制无功在外界因素较为稳定时，无功总量最低，削减电网成本。其余两种控制方法的无功输出在场景变化时，都会出现明显下降，在稳定状态无功输出会增加，无功功率输出如图4所示。

图4 不同控制下的无功功率

综上所述：基于并网点电压控制与恒功率控制效果较差，恒功率因数cosφ控制比较灵活，它会随着系统有功功率的改变，不断调节光伏系统输出的无功功率，外界环境发生剧烈的光照或温度变化时，有功出力也相应增加，难免出现并网点电压越限问题；基于有功出力cosφ(P)控制能够基于输出的有功功率调整功率因数，并网点电压、功率因数、无功功率控制效果都优于cosφ控制效果，可以有效实现对分布式光伏系统无功控制。

4 结语

四种无功控制对电压越限的控制各有利弊。恒无功功率Q控制方法简单，灵活性不强，光照强度急剧变化时，功率因数会超出规定范围；恒功率因数cosφ控制相对灵活，但有功出力不断增加时，依然会出现电压越限问题；基于光伏有功出力cosφ(P)控制可以有效地控制并网点电压，但是会增加无功消耗，增加电网运行成本；基于并网点电压Q（U）控制的优势为无功总量最低，削减电网成本，其不足是调压能力相对较弱。

针对不同电压等级的并网系统，为解决大型光伏发电系统并网所带来的电压越限问题，在无功功率控制方面有待进一步研究。