应用于圆饼工件分拣的码垛机器人自适应积分滑模控制

王洪波，姚嘉凌

应用于圆饼工件分拣的码垛机器人自适应积分滑模控制

王洪波1，姚嘉凌2

（1.江苏安全技术职业学院 交通与安全学院，江苏 徐州 221011；2.南京林业大学 汽车与交通工程学院，南京 210037）

针对存在系统未建模特性和负载变化下码垛机器人关节空间轨迹跟踪控制的问题，设计一种基于结合时延估计技术与自适应积分滑模面的控制策略。根据圆饼工件分拣需求，设计一款桌面式码垛机器人系统，推导机器人的运动学与动力学模型，给出关节空间轨迹规划算法，并基于无模型思想设计关节空间轨迹跟踪控制器。利用雅克比伪逆法可反解出机器人的关节角；通过所提的轨迹规划算法能有效获得各关节运动轨迹；与PID控制器和积分滑模控制器相比，文中所提控制器具有较好的控制精度、较强抗干扰性和较高的鲁棒性。仿真和实验结果表明，所设计的基于时延估计技术的自适应积分滑模控制器是合理的，能使得码垛机器人完成圆饼工件的分拣任务，具有一定的工程应用价值。

码垛机器人；积分滑模；时延估计；关节空间；轨迹跟踪控制

在人口红利消失、劳动力严重短缺的形势下，“机器换人”成为大势所趋，是制造业转型升级的必由之路。例如，在劳动力密集、工作内容枯燥、作业环境恶劣的码垛行业，传统的人工码垛与机械式码垛已经不能适应工业发展，而高精度、小能耗、安全稳定的码垛机器人逐渐被市场所接受[1-3]。对于码垛机器人等一类关节型工业机器人而言，设计高精度、高可靠性的控制器一直是工程师和学者们追求的目标。由于制造、装配、疲劳损耗等因素的存在，会导致码垛机器人关节处产生摩擦和间隙，同时末端执行器负载变化与系统所处环境的不确定性都会影响控制器的性能，给控制器的设计带来一定的难度。

为解决上述问题，不少先进控制策略被引入到工业机器人的高精度控制中，像迭代学习控制[4]、自适应鲁棒控制[5]、模糊控制等[6-7]，但大多数研究仅停留在仿真层面而没有在实验条件下对控制算法的可行性进行验证。滑模控制（Sliding Mode Control，SMC）是一种结构简单、参数少、易于工程实现的鲁棒控制方法，常被应用于工业机器人实际控制中。然而，SMC固有的抖振现象会给机器人的机械结构和电子元件造成损坏。为此，学者们尝试改进原有SMC的结构来提高其控制性能。例如，冒建亮等设计了一种快速连续非奇异终端滑模面，使得滑模面切换时连续可导，从而有效地抑制了系统抖振，并保证良好的系统动态性能[8]。Dumlu[9]也将分数阶理论与自适应积分滑模结合来实现六轴机器人状态量的有限时间收敛，并抑制控制量的抖振，同时积分滑模函数亦可降低系统静态误差，使得系统具有较好的稳态过程。近年来，时延估计（Time Delay Estimation，TDE）技术常被引入到机器人控制结构中，可用来估计系统的非线性和不确定性[10-11]。将自适应积分滑模面与TDE结合，可以在不需要精确机器人模型的基础上设计出鲁棒性较高的控制策略，从而保证机器人在关节空间轨迹跟踪的精度。根据不同颜色的圆饼工件的分拣任务，文中设计一款桌面式码垛机器人系统。同时，建立码垛机器人的运动学和动力学模型，并给出了关节空间轨迹规划算法。进一步地，引入TDE技术来补偿系统中的不确定性因素与外界干扰，并设计自适应积分控制算法来保证各关节状态量的快速响应与较高的跟踪精度。最后，通过仿真和实验验证了文中所提方法的有效性。

1 系统描述

1.1 码垛机器人系统

文中的设计目标为利用六轴码垛机器人将红、黄、蓝3种圆饼按照颜色分拣堆放。设计的码垛机器人系统的虚拟样机见图1，其工作原理为上料架上的圆饼由气缸推送至输送带上，经长距离RGB颜色传感器获得颜色后，将圆饼信息发送至上位机，进而驱动机器人按照设定好的运动轨迹将圆饼码放至下料架指定圆形沉孔内。系统选用的是新时达SD500桌面式机器人，腕部额定负载为3 kg，最大负载为5 kg，可达工作半径为500 mm，其任务指标为在规定节拍内将不同颜色的圆饼从输送带上码放至下料架上的沉孔内，并按照预设的颜色位置放置。输送带的运动速度可通过变速箱中的交流变频电机来调节。显示器作为上位机可以实时监控系统的工作状态。机器人的控制系统被放置在工装台的柜内，包括机器人运动控制板卡和PLC。其中，运动控制卡主要负责对码垛机器人的伺服控制，PLC负责控制长距离RGB颜色传感器、输送带、启动开关等外围设备。

图1 码垛机器人系统的虚拟样机

1.2 运动学分析

码垛机器人的拓扑结构是串联开链式的，见图2。在各个关节轴上添加连杆坐标系，采用标准的Denavit–Hartenberg（DH）参数[12]来描述其结构，见表1。

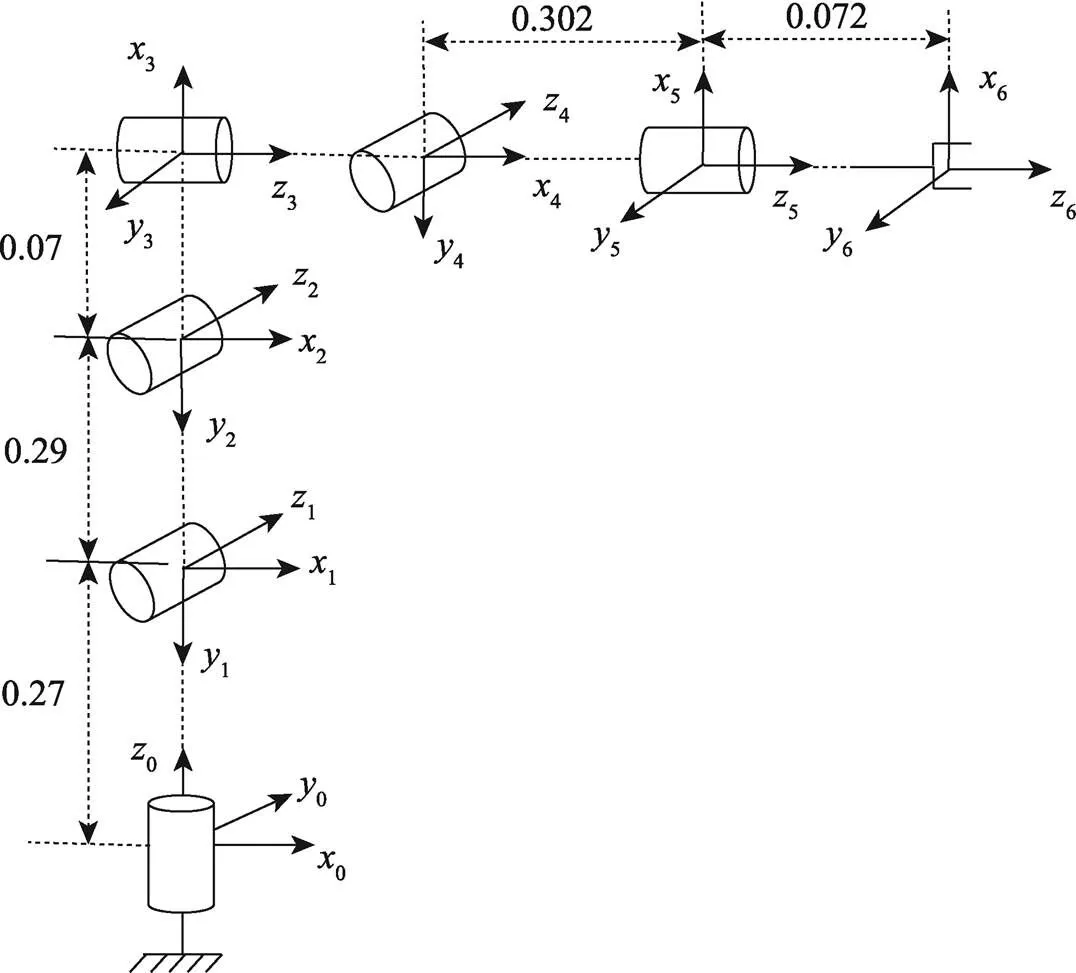
图2 码垛机器人的拓扑结构

表1 六轴码垛机器人的DH参数

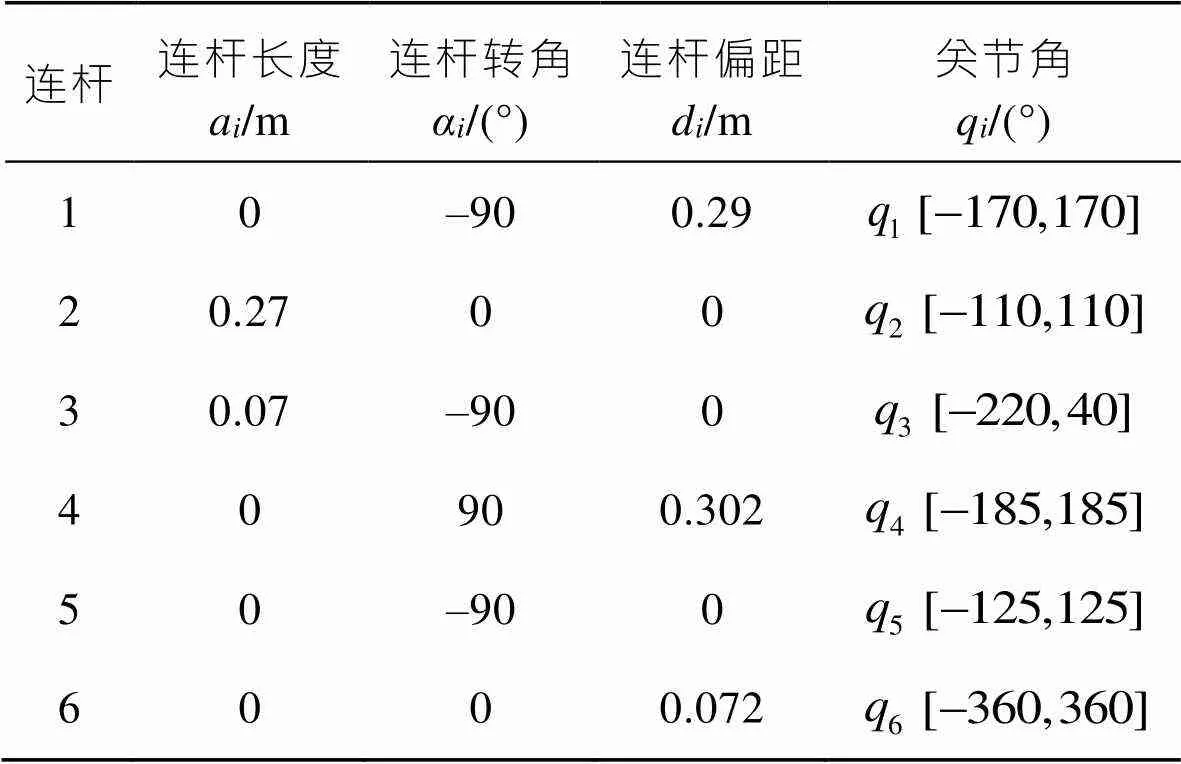
Tab.1 DH parameters of 6-DOF palletizing robot

根据连杆变换的递推公式可得到六轴码垛机器人的正向运动学方程为：

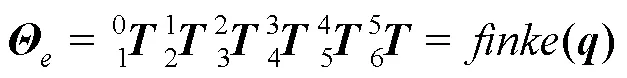
对式（1）求关于时间的一阶导数，有：

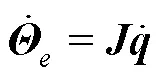
进而，可得到雅克比矩阵的伪逆为[13]：

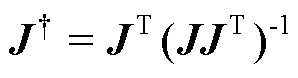
联立式（1）和式（3）可得码垛机器人的运动学逆解为：

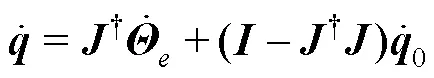
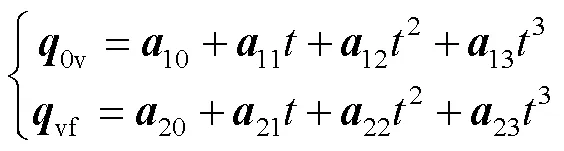
1.3 动力学分析

不失一般性地，码垛机器人的刚体动力学方程可由Euler–Lagrange方程推导出来，其紧凑形式为[14]：

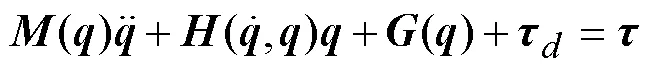
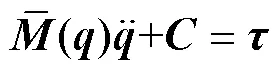
2 控制器设计

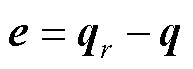
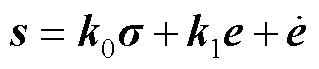
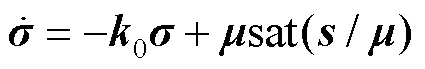
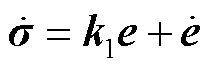
基于上述分析，可设计一个自适应控制律来调节积分器的能力：

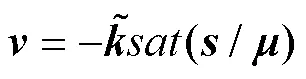
对于式（8）求关于时间的导数，有：

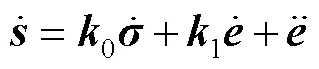
联立式（6）、（11）和（12），并引入TDE技术[16]，可推导出关节控制力矩为：

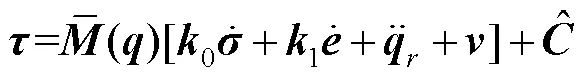
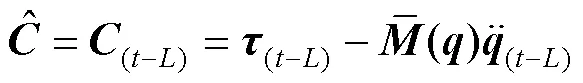
接下来，对控制器（13）的稳定性分析。选择一个标准的Lyapunov函数为：

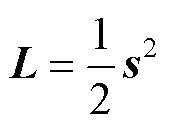
将式（6）、（9）和（12）代入到式（10）中，有：

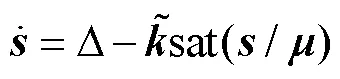
对于式（15）求导，并联立式（7）、（9）和（12），有：

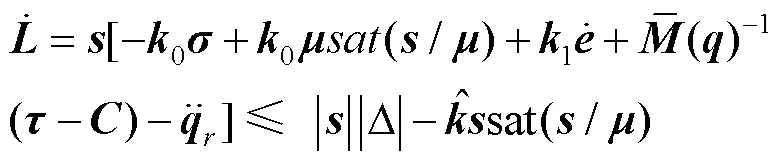
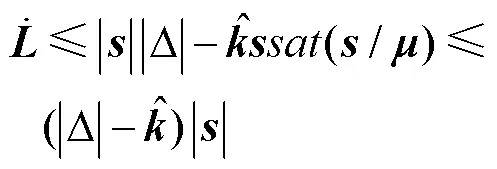
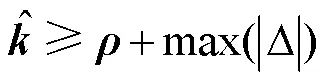
3 结果分析

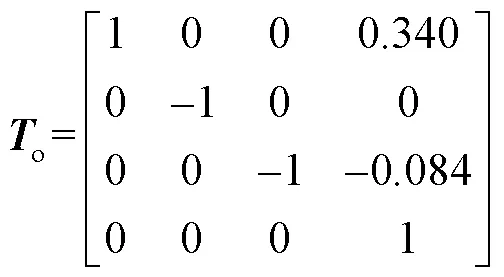
选用的SD500码垛机器人含有6个NIDEC– MX–201伺服电机和6套Ruking SEA3–02NR 驱动器。在关节空间轨迹跟踪控制实验中，将上位机中MATLAB/Simulink搭建好的控制算法编译后生成嵌入式代码，并下载到实时仿真器中；仿真器输出伺服驱动器的控制信号，实现对伺服电机的控制；最后，伺服电机将采集到的关节角信号反馈到上位机形成闭环控制，采样频率为1 000 Hz。需要注意的是，关节角速度信号与角加速度信号可通过差分法计算获得，整个实验的过程见图10。

图3 码垛机器人系统样机

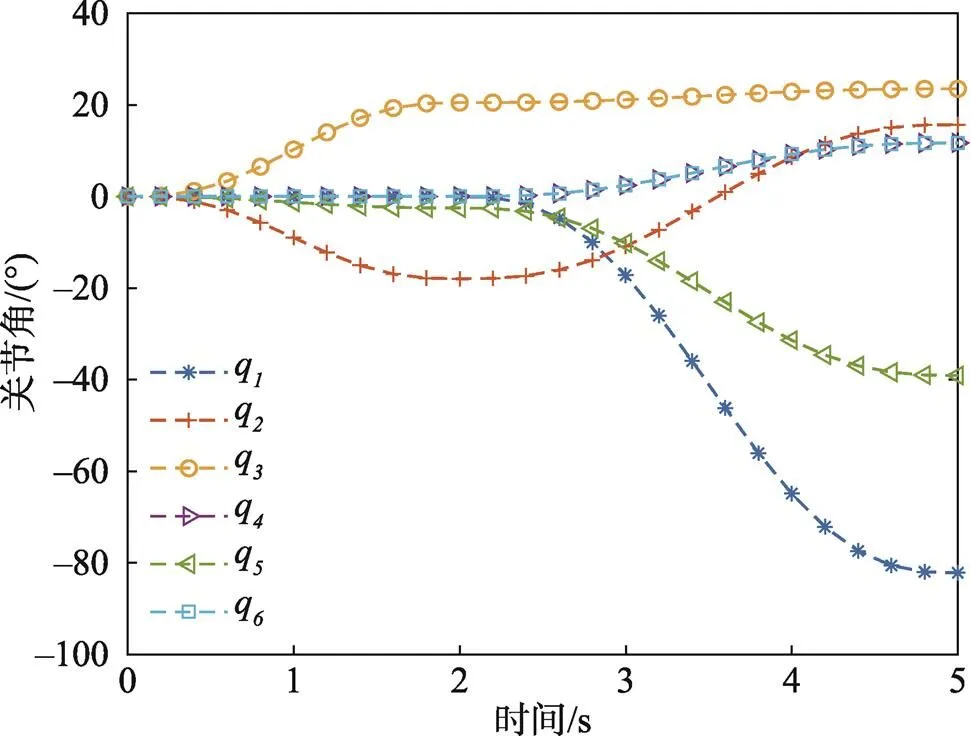
图4 规划好的关节角

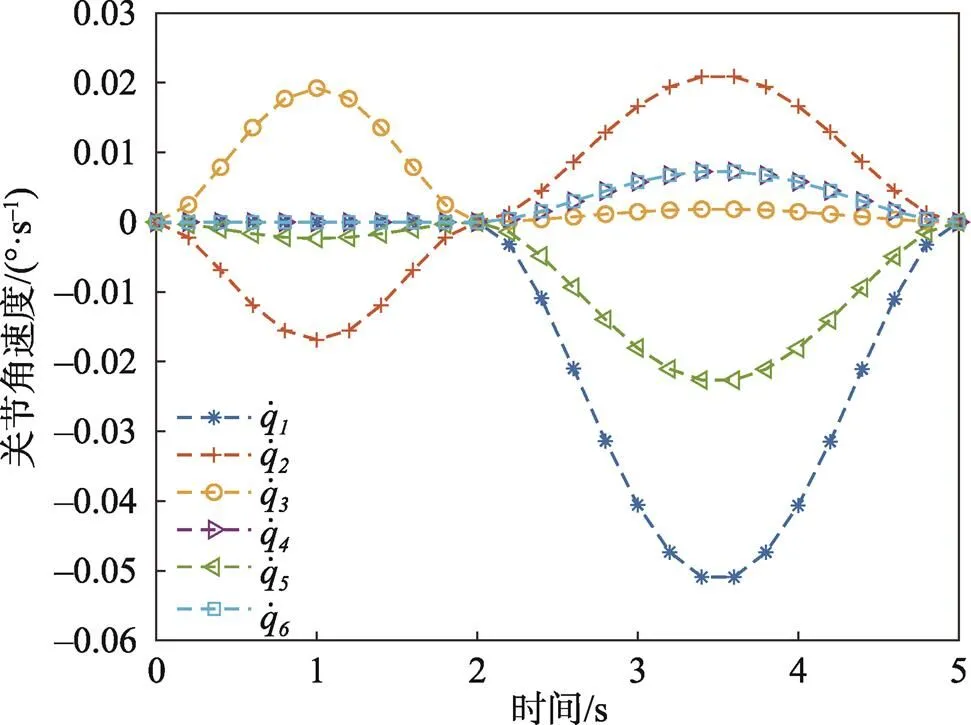
图5 规划好的关节角速度

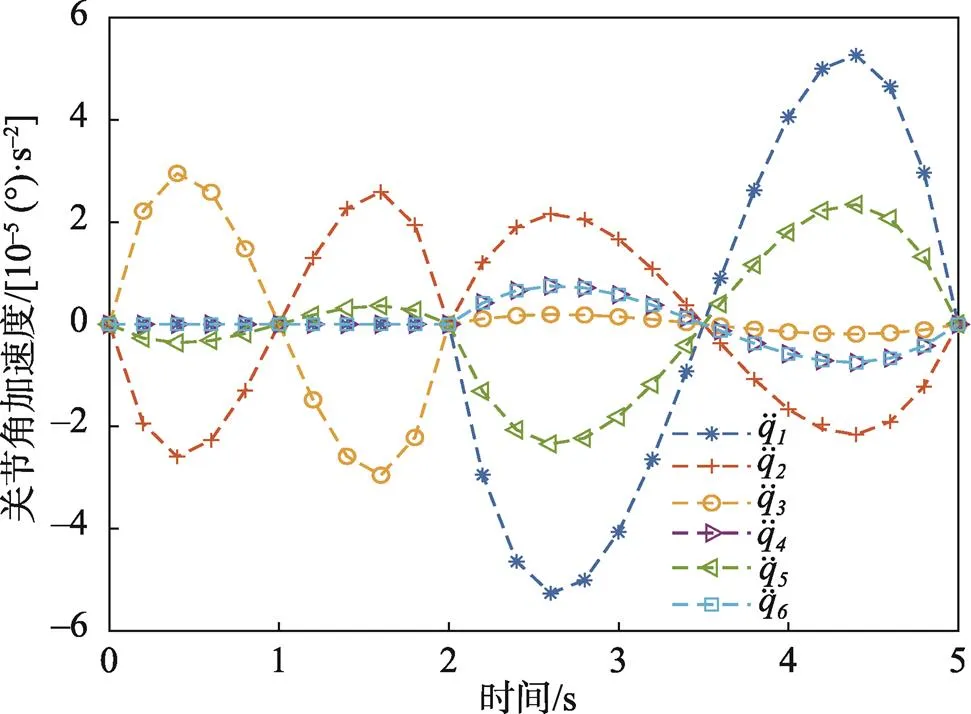
图6 规划好的关节角加速度

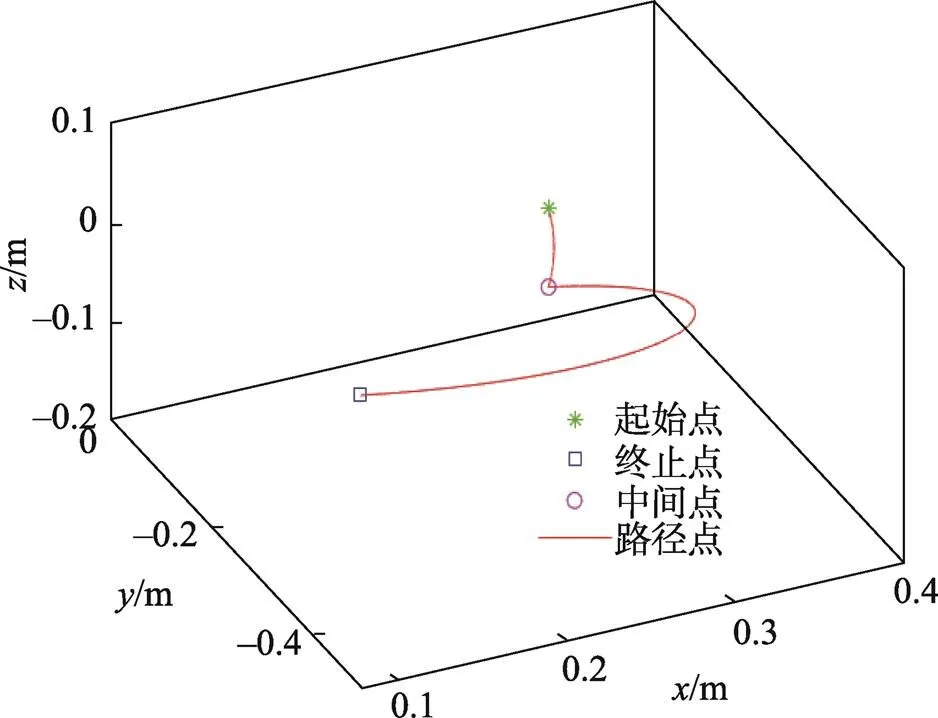
图7 末端执行器的三维轨迹

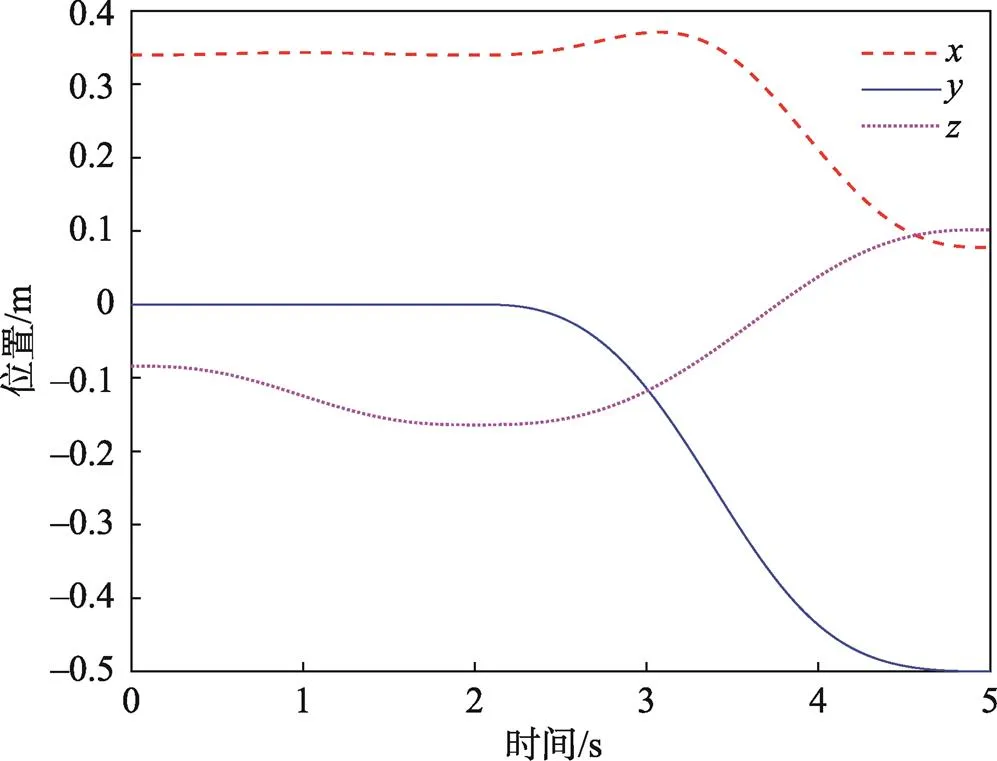
图8 末端执行器位置变化

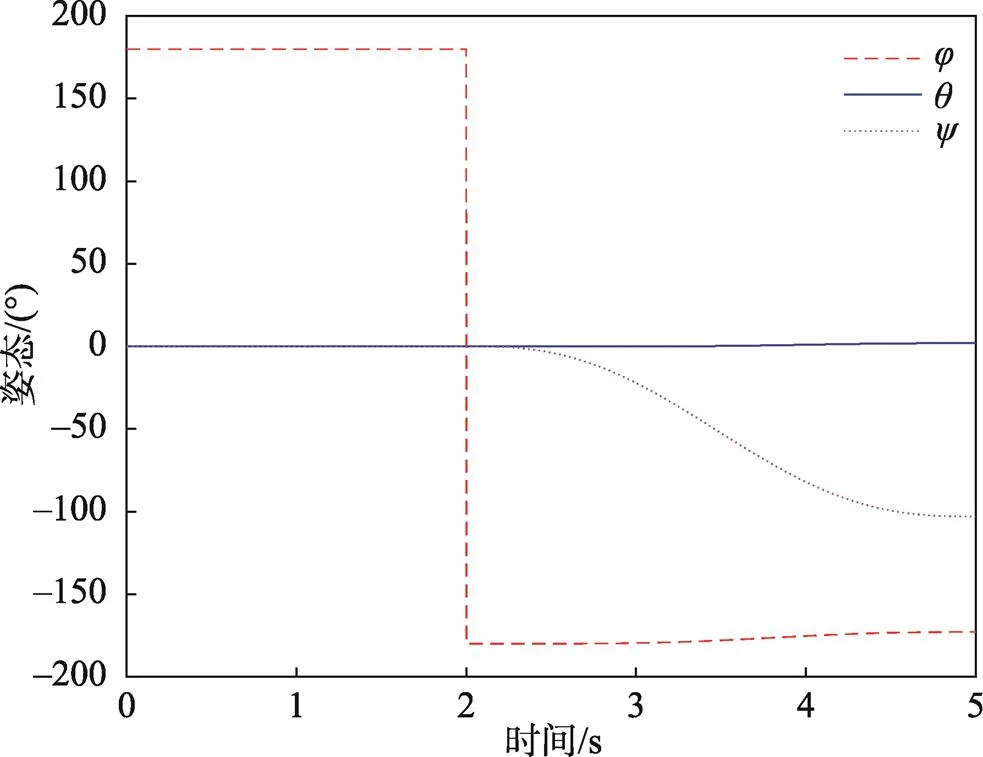
图9 末端执行器姿态变化

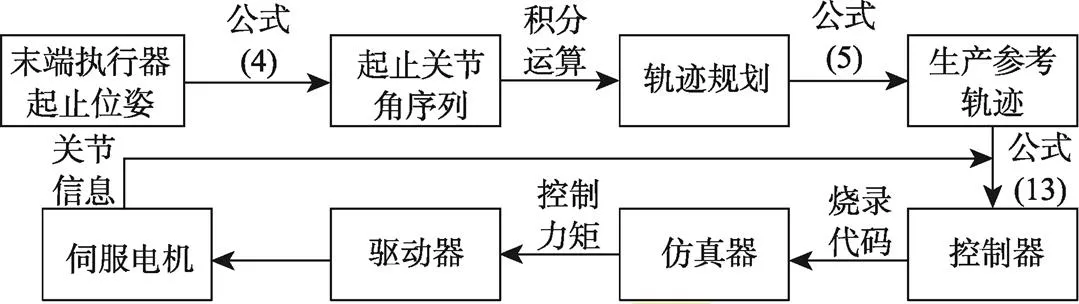
图10 实验流程

同时，为了测试文中所设计的基于TDE技术的适应积分滑模控制器的性能，选择文献[17]中提出的双积分滑模控制器（ISMC）和文献[18]提出的PID控制器与之进行比较。3种控制策略的控制参数均通过人工试凑的方式确定，见表2。这里需要指出的是，ISMC和PID中控制参数的解释详见参考文献，文中不再过多描述。

图11给出了3种控制器作用下码垛机器人各关节的跟踪效果，可以看出3种控制器均能使各关节较好地跟踪上参考轨迹，这表明通过人工试凑获得各控制器参数是合理有效的。另外，在图12中给出了各关节的跟踪误差曲线，可以很明显地看出文中控制器的跟踪精度要优于ISMC和PID。这也说明文中控制器的TDE技术可以很好地估计码垛机器人中的未建模特性和外界负载变化，积分环节也可以较好地消除系统输出的静态误差，使得控制器具有较高的鲁棒性。

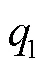
表2 3种控制器的参数

Tab.2 Parameters of the three controllers

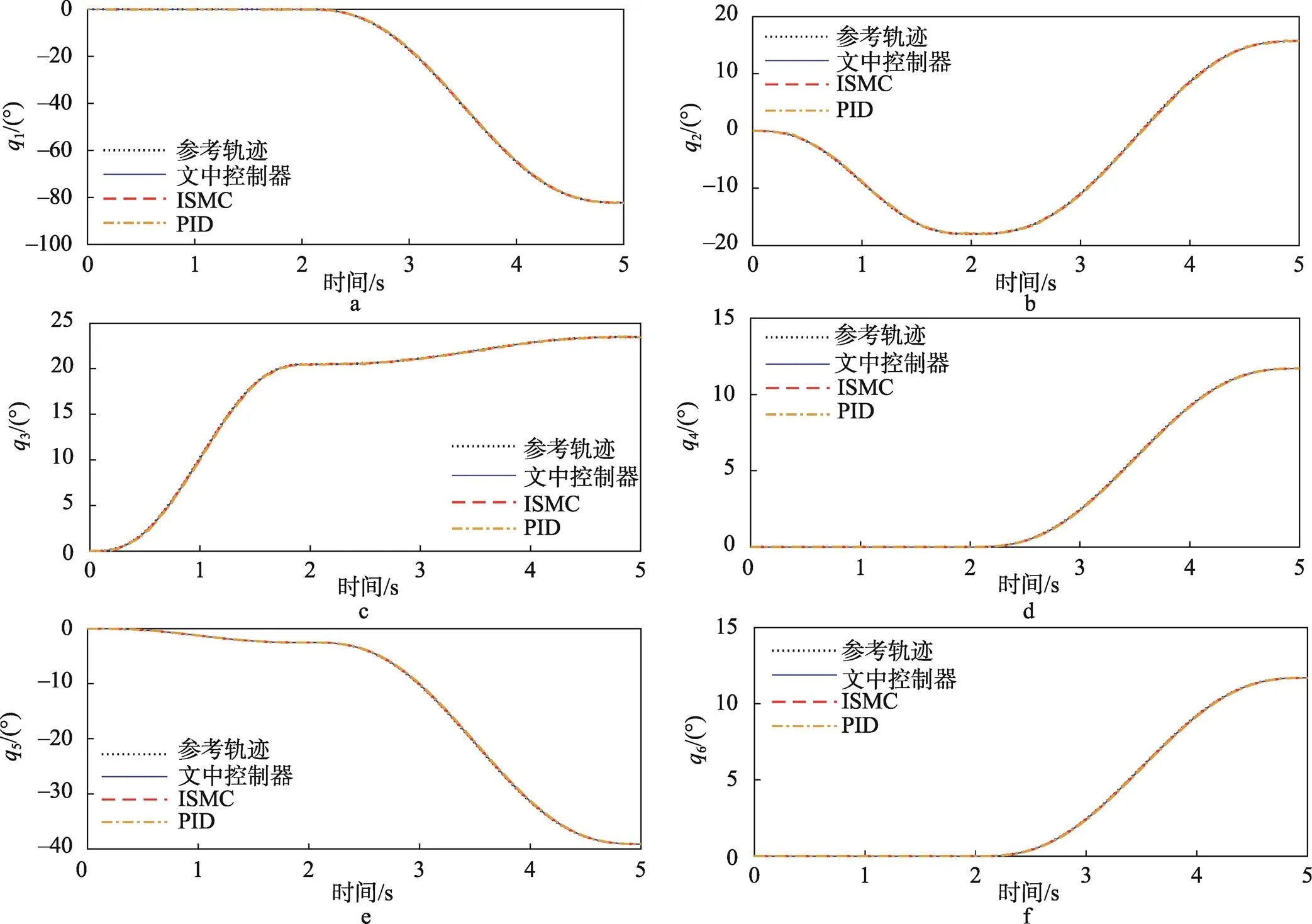
图11 关节角的跟踪响应

­­­­

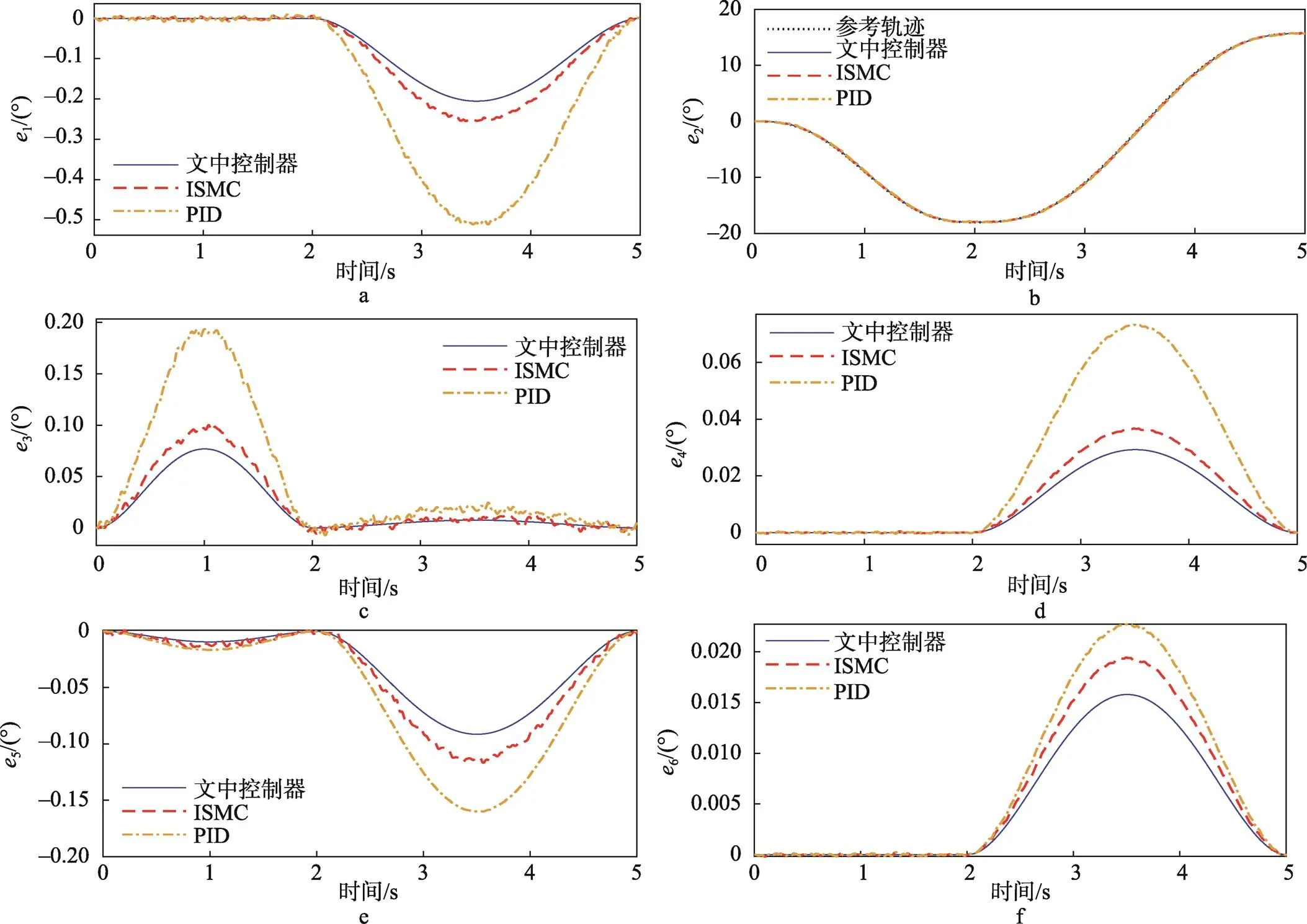
图12 关节角的跟踪误差

表3 3种控制器下的MAE值和RMSE值

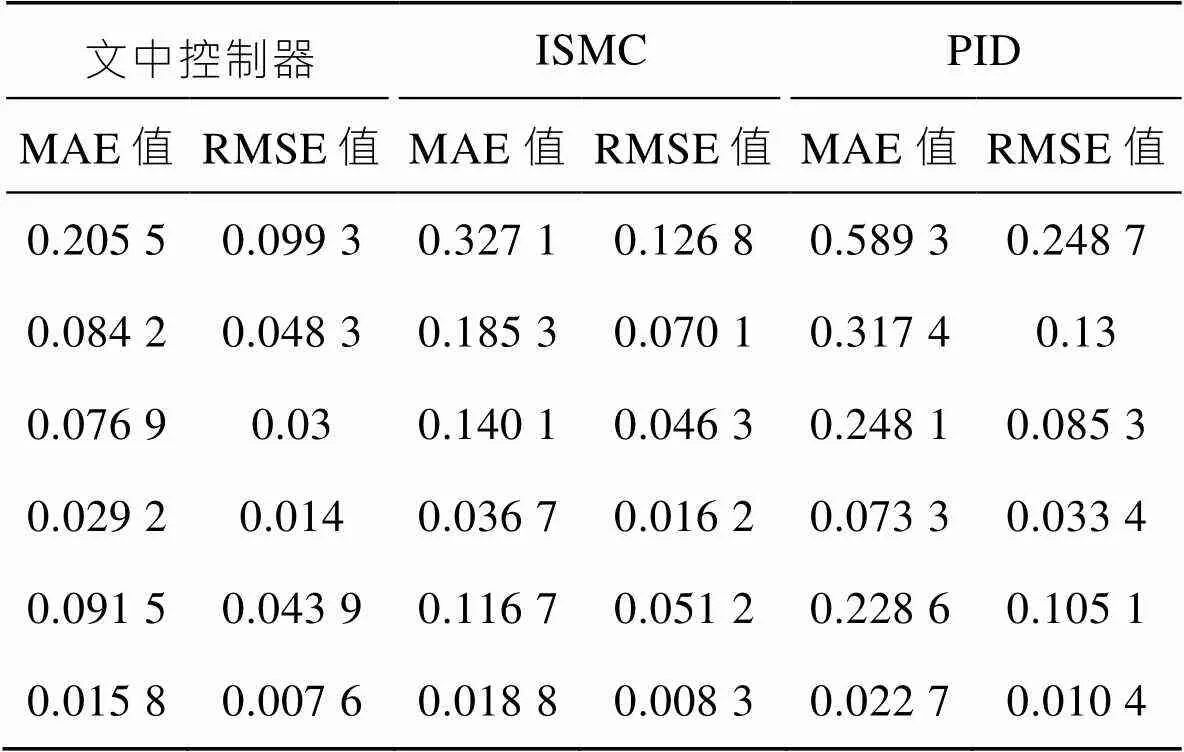
Tab.3 MAE and RMSE of the three controllers

4 结语

文中设计了一种结合TDE技术和自适应ISMC的控制策略来解决码垛机器人关节空间轨迹跟踪控制问题，从而提高不同颜色圆饼工件的分拣质量，得到的主要结论有：设计了一款面向圆饼工件分拣的码垛机器人系统，包括输送带、显示器、上下料架、机器人、长距离RGB颜色传感器等，并详细地阐述了该机器人的工作原理；建立了码垛机器的运动学模型与动力学模型，并给出了关节空间内轨迹规划算法；设计了自适应积分滑模控制器来实现关节角的跟踪控制，并用TDE来估计和补偿系统的未建模特性与外界干扰；与PID和ISMC相比，文中控制器的MAE值和RMSE值最小，具有较高的跟踪精度、较高的鲁棒性和较强的抗干扰性。

在今后的研究中，会进一步研究其他控制算法来提高码垛机器人的控制性能。同时，也会基于机器视觉研究工件位姿快速定位算法，提高码垛机器人的工作效率。

[1] 权宁, 徐志鹏. 基于视觉的工业机器人码垛系统设计与分析[J]. 包装工程, 2021, 42(15): 233-238.

QUAN Ning, XU Zhi-peng. Design and Analysis of Industrial Robot Palletizing System Based on Vision[J]. Packaging Engineering, 2021, 42(15): 233-238.

[2] 朱洪雷, 代慧, 罗隆. 基于自动包装码垛技术的码垛机器人研究[J]. 包装工程, 2020, 41(13): 231-236.

ZHU Hong-lei, DAI Hui, LUO Long. Palletizing Robot Based on Automatic Packaging Palletizing Technology[J]. Packaging Engineering, 2020, 41(13): 231-236.

[3] 李远, 农秉茂. 包装搬运机器人运动轨迹优化设计[J]. 包装工程, 2020, 41(1): 123-127.

LI Yuan, NONG Bing-mao. Optimization Design of Moving Trajectory for Packaging Handling Robot[J]. Packaging Engineering, 2020, 41(1): 123-127.

[4] PENG Cheng, WANG Cong, TOMIZUKA M, et al. Robust Iterative Learning Control for Vibration Suppression of Industrial Robot Manipulators[J]. Journal of Dynamic Systems, Measurement, and Control, 2016, 140(1): 011003.

[5] YIN X, PAN L. Direct Adaptive Robust Tracking Control for 6 DOF Industrial Robot with Enhanced Accuracy[J]. ISA Transcation, 2018, 72: 178-184.

[6] LIAN R J. Intelligent Controller for Robotic Motion Control[J]. IEEE Transactions on Industrial Electronics, 2011, 58(11): 5220-5230.

[7] 洪槐斌, 刘雯华, 张进杰. 往复式压缩机气量调节工况下的内模解耦PID控制策略研究[J]. 流体机械, 2021, 49(10): 29-35.

HONG Huai-bin, LIU Wen-hua, ZHANG Jin-jie. Research on Decoupling IMC-PID Control Strategy for Reciprocating Compressor under the Condition of Stepless Flow Control[J]. Fluid Machinery, 2021, 49(10): 29-35.

[8] 冒建亮, 李奇, 朱海荣. 一种连续非奇异快速终端滑模控制方法[J]. 控制与决策, 2016, 31(10): 1873-1878.

MAO Jian-liang, LI Qi, ZHU Hai-rong. A Continuous Nonsingular Fast Terminal Sliding Mode Control Method[J]. Control and Decision, 2016, 31(10): 1873-1878.

[9] DUMLU A. Design of a Fractional-Order Adaptive Integral Sliding Mode Controller for the Trajectory Tracking Control of Robot Manipulators[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2018, 232(9): 1212-1229.

[10] LEE J, CHANG P H, JIN M. Adaptive integral sliding mode control with time-delay estimation for robot manipulators[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6796-6804.

[11] GHAF-GHANBARI P, MAZARE M, TAGHIZADEH M. Active Fault-Tolerant Control of a Schonflies Parallel Manipulator Based on Time Delay Estimation[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 1-18.

[12] FU Bing, 0016 L C, ZHOU Yun-tao, et al. An Improved A* Algorithm for the Industrial Robot Path Planning with High Success Rate and Short Length[J]. Robotics and Autonomous Systems, 2018, 106: 26-37.

[13] GARDUÑO-APARICIO M. A Multidisciplinary Industrial Robot Approach for Teaching Mechatronics-Related Courses[J]. IEEE Transactions on Education, 2017, 61(1): 55-62.

[14] FEDERICO R, FREDERIC B, JORGE D, et al. Discrete Cosserat Approach for Multisection Soft Manipulator Dynamics[J]. IEEE Transactions on Robotics, 2018, 34(6): 1518-1533.

[15] DAO H, TRAN D, AHN K. Active Fault Tolerant Control System Design for Hydraulic Manipulator with Internal Leakage Faults Based on Disturbance Observer and Online Adaptive Identification[J]. IEEE Access, 2021, 9: 23850-23862.

[16] KALI Y, SAAD M, BENJELLOUN K, et al. Super-Twisting Algorithm with Time Delay Estimation for Uncertain Robot Manipulators[J]. Nonlinear Dynamics, 2018, 93(2): 557-569.

[17] 刘金琨. 机器人控制系统的设计与MATLAB仿真[M]. 北京: 清华大学出版社, 2008: 487-494.

LIU Jin-kun. Design of Robot Control System and MATLAB Simulation[M]. Beijing: Tsinghua University Press, 2008: 487-494.

[18] CHEAH C, KAWAMURA S, ARIMOTO S. PID Control of Robotic Manipulator with Uncertain Jacobian Matrix[C]// Proceedings 1999 IEEE International Conference on Robotics and Automation, IEEE, 1999, 1: 494-499.

Adaptive Integral Sliding Mode Control of Palletizing Robot System for Round Piece Sorting

WANG Hong-bo1,YAO Jia-ling2

(1. School of Transportation and Safety, Jiangsu College of Safety Technology, Jiangsu Xuzhou 221011, China; 2. College of Automobile and Traffic Engineer, Nanjing Forestry University, Nanjing 210037, China)

The work aims to propose a control strategy combing time delay estimation technique and adaptive integral sliding mode for trajectory tracking control in joint space of palletizing robot under unmodeled characteristics and load variation. According to the sorting requirements of round pieces, a desktop palletizing robot system was designed. The kinematics and dynamics models of the robot were derived to obtain the trajectory planning algorithm in joint space. Then, the trajectory tracking controller in joint space was designed based on the model-free idea. The joint angles of the robot were obtained by the Jacobi pseudo-inverse method and the trajectory of each joint was acquired through the proposed trajectory planning algorithm. Compared with PID controller and integral sliding mode controller, the proposed controller had better control accuracy, stronger disturbance rejection and higher robustness. The simulation and experiment results prove that the adaptive integral sliding mode controller designed based ontime delay estimation technique is reasonable and can help the palletizing robot deal with the tasks of round pieces sorting, which has a certain engineering value.

palletizing robot; integral sliding mode; time delay estimation; joint space; trajectory tracking control

TB486；TP242

A

1001-3563(2022)15-0281-08

10.19554/j.cnki.1001-3563.2022.15.033

2021–10–13

国家自然科学基金（51975299）；江苏省自然科学基金（BK20181403）

王洪波（1983—），男，本科，江苏安全技术职业学院讲师，主要研究方向为载运工具运用工程、机器人技术。

责任编辑：曾钰婵